基于先验知识和模糊C均值聚类算法的脑部磁共振图像分割研究
2019-07-16张玉柱王传兵
张玉柱 王传兵*
磁共振成像(magnetic resonance imaging,MRI)是诊断脑代谢疾病的重要手段,脑代谢疾病往往伴随着脑组织形态的改变,精准医学需要定量评估脑部各组织区域和肿瘤病灶大小的变化,往往需要借助图像分割技术[1]。图像分割最早采用手工分割,但因耗时较长、主观差异性大以及不利于病灶监测等缺点逐渐被自动分割所替代[2-3]。
近年来,涌现出多种脑部MR分割算法,主要包括基于阈值、基于区域、像素分类和基于模型的分割算法,其中基于阈值的分割算法仅借助图像灰度直方图获取单个或者多个阈值,不能充分利用图像像素信息,且最佳阈值较难获取[4-6]。区域生长算法从初始种子点开始,根据一定相似性准则,将图像中与种子点相似的像素归为一类,该算法对初始种子点选取和迭代终止条件要求较高。基于模型的分割算法主要将不断变形的维曲线(面)作为零水平集嵌入到更高一维的函数中,由封闭超曲面的演化方程得到函数的演化方程,而嵌入的封闭曲线(面)则保持为函数的零水平截面上的点集,即为最终轮廓线,模型算法相对复杂,且对图形拓扑结构要求较高。像素分类算法最常用的是模糊C均值(fuzzy c-means method c-mean,FCM)聚类算法,可同时分割多种组织,但对初始聚类中心比较敏感,选择不当容易陷入局部最优解,且导致迭代收敛较慢。为此,提出重构目标函数、局部空间信息、邻域灰度等多种改进方法,但均收效甚微。本研究旨在提出基于先验知识引导的FCM算法(prior-information-guided fuzzy c-means,PIGFCM),通过先验知识实现聚类中心初始化,提升聚类中心收敛性能。
1 研究方法
1.1 标准FCM算法
传统的聚类分析是将每个元素严格划分到一个类中,属于硬划分。FCM是将聚类生成的每个簇均看做模糊集合,通过每个样本点对所有类别中心的隶属度来确定聚类关系,是一种柔性划分,使得被划分到同一簇的样本点之间相似度最大,而不同簇之间的相似度最小[7]。假设图像像素总数为N,图像像素集合为Y={y1,y2,…yi…yN},图像分为K(K≥2)个类别,表明每个像素点可以属于多个类别,记第c个类别聚类中心为Vc,对于任意像素点,第i个像素属于第c类的隶属度函数记为µic,c∈[1,K],K为分类数目,隶属度函数满足公式1:
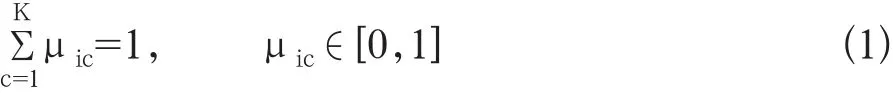
则图像分割过程转化为像素分类问题,像素分类的目标函数见公式2:
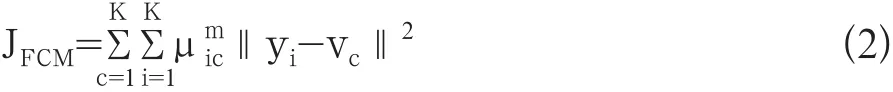
式中m为隶属度函数的权重系数,决定分类结果的模糊程度,常取2。
求隶属度函数约束条件下的目标函数极小值,可采用拉格朗日乘数法构造新的目标函数,如公式3:
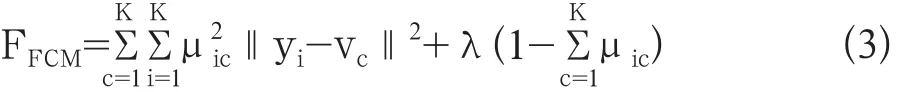
对求偏导,可得各类别聚类中心和各像素隶属度,其计算为公式4和公式5:
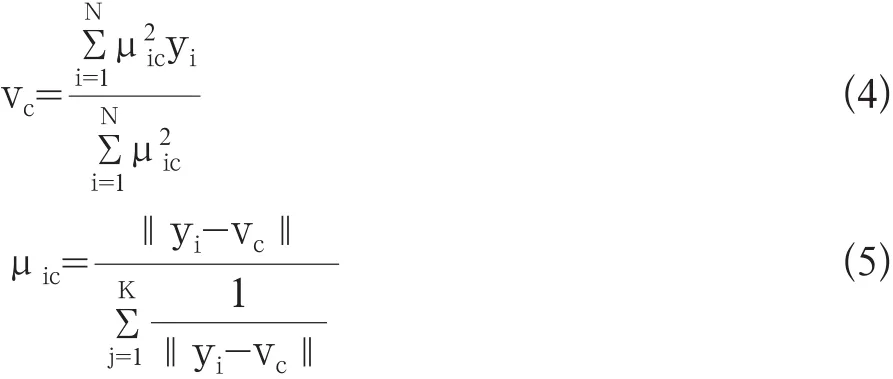
1.2 改进的FCM算法
FCM聚类算法实现简单,最大的缺陷是初始聚类中心选取对噪声等孤立点和分布不均较为敏感,容易陷入局部最优解,且增加计算量[8]。FCM聚类改进算法很多,采用图像先验知识快速确定FCM初始聚类中心,利用先验知识函数构建新的目标函数,其计算为公式6:
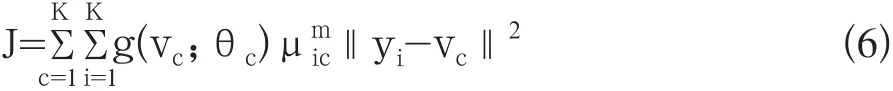
式中g(vc;θc)函数项表示关于聚类中心vc和参数θc的先验知识。
新目标函数的求解同样采用拉格朗日乘数法,其计算为公式7:
对λ,vc,µic求偏导,可得各类别聚类中心和各像素隶属度,其计算为公式8和公式9:
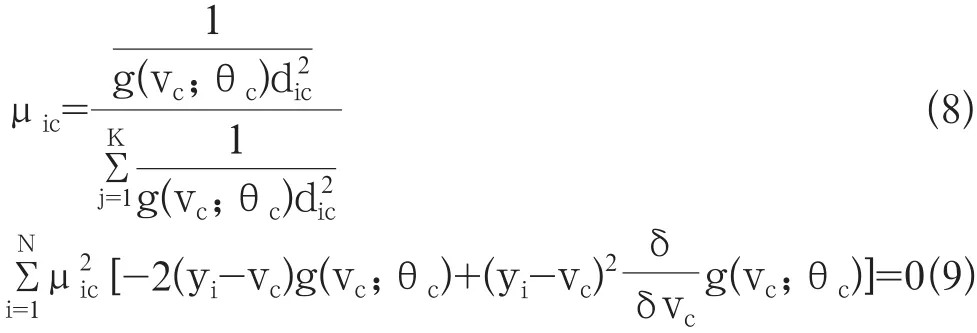
如果聚类中心满足均匀分布,则基于此先验知识的改进FCM算法等同于标准FCM算法。本研究采用高斯分布作为先验知识函数确定初始聚类中心,避免盲目性,则聚类中心vc~N(µc,σc2),µc,为聚类中心均值,σc2为聚类中心的方差,表示先验信息相对聚类中心的不确定性,则先验知识g(vc;θc)反映第c类聚类中心分布,其计算为公式10:
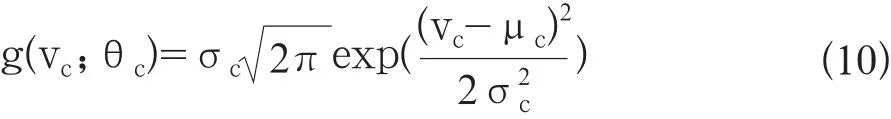
求得µc和vc和将公式(10)带入公式(9)得到计算公式11和公式12:
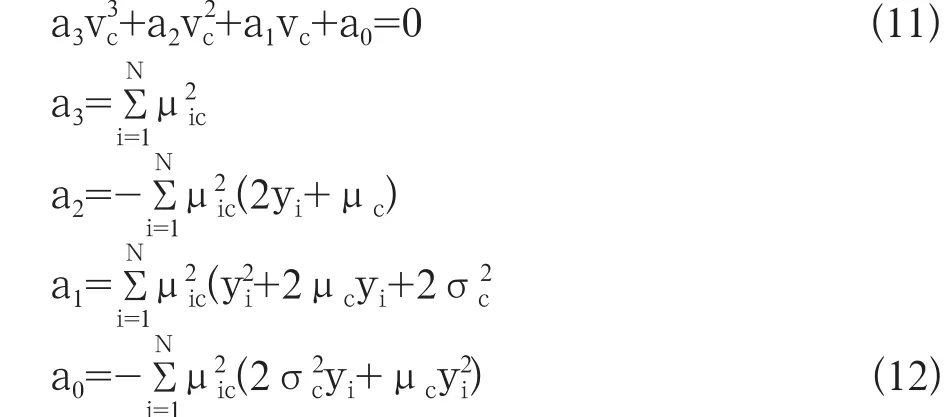
因此,基于先验知识引导的FCM算法步骤如下:①设定聚类数目K和迭代停止参数;②基于高斯分布设置初始聚类中心,{µc,σc},c=1,…,k;③在满足隶属度约束条件下,采用0~1随机初始化所有像素点的隶属度函数;④设置迭代计数b=0,使用公式(8)和(10)计算和更新隶属度函数与各类聚类中心;⑤当||<ε时,此处ε取10-5,算法收敛,得到各类的聚类中心和各像素对各类的隶属度值,完成模糊聚类划分,否则跳转到步骤④。
1.3 图像分割效果评价
图像分割效果定量评估采用Dice相似性系数、均方根误差(root mean square error,RMSE)和算法平均耗时[11-13]等指标,Dice相似性系数越大,RMSE和平均耗时越小,图像分割越精确,其计算为公式15和公式16:
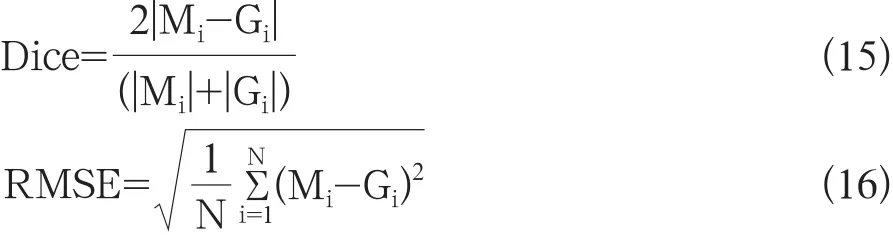
式中Dice、M、G、RMSE和N分别表示Dice相似性系数、分割所得组织区域、真实组织区域、均方根误差和像素总数。
2 结果
为了验证本研究分割算法的可行性、优越性和实用性,选用MR脑图库中人工合成图像和临床实例图像进行模拟实验,所有仿真实验均在Matlab2013a平台上实现。采用文献报道的其他分割算法与本研究提出的算法进行比较,分别为标准FCM[14]、基于邻域的FCM算法(neighborhood FCM,NFCM)[15]、基于非局部的FCM算法(non-local FCM,NL-FCM)[16]、基于非局部强健的FCM算法(non-local rubust FCM,NL-R-FCM)[17]、基于非局部正则化算法(non-local regularization,NL-Reg)[18]以及强健FCM算法(rubust FCM,RFCM)。
2.1 仿真图像的分割结果
(1)图像仿真实验对象为20幅T1加权MR图像(噪声水平为0%~9%,不均匀性为0%~40%),其中10幅MR脑图像被用来训练获得先验知识参数µc和σc,经Kolmogorov-Smirnov检验可知各类别聚类中心均显著符合高斯分布(D=0.563,P<0.01),剩下10幅图像用于测试。采用FCM算法的MR图像分割结果,可以显示出脑部各组织分割精确完整(图1)。
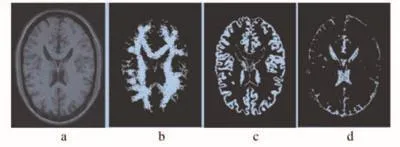
图1 基于本研究算法的仿真MR图像分割
(2)不同分割算法和噪声水平对应的脑白质和灰质平均Dice相似性系数,其结果显示,随着噪声水平升高,各分割算法的分割精度总体上随之下降,不同分割算法对噪声敏感度差异较大,基于NL-Reg的图像分割算法对噪声最敏感,其次是标准的FCM、NFCM、NL-R-FCM和NL_FCM改善较大。基于本研究提出的PIGFCM算法分割效果最佳,白质Dice相似性系数可达0.93~0.98,灰质Dice相似性系数可达0.87~0.96(见表1)。
(3)不同聚类中心初始化方法对分割算法的影响,基于先验知识的聚类中心初始化方法获得的平均Dice相似性系数均小于随机分配方法,其中FCM算法的平均Dice相似性系数保持不变,NFCM算法从0.91提升到0.92,PIGFCM算法从0.95提升到0.97。三种算法的RMSE均有所提升,且本研究提出的PIGFCM算法平均耗时是NFCM算法的0.17倍,FCM算法的0.81倍。表明本研究提出的先验知识模型能提升FCM算法分割性能,且本研究提出的分割算法具有更强的收敛性、抗噪性和分割精确度(见表2)。
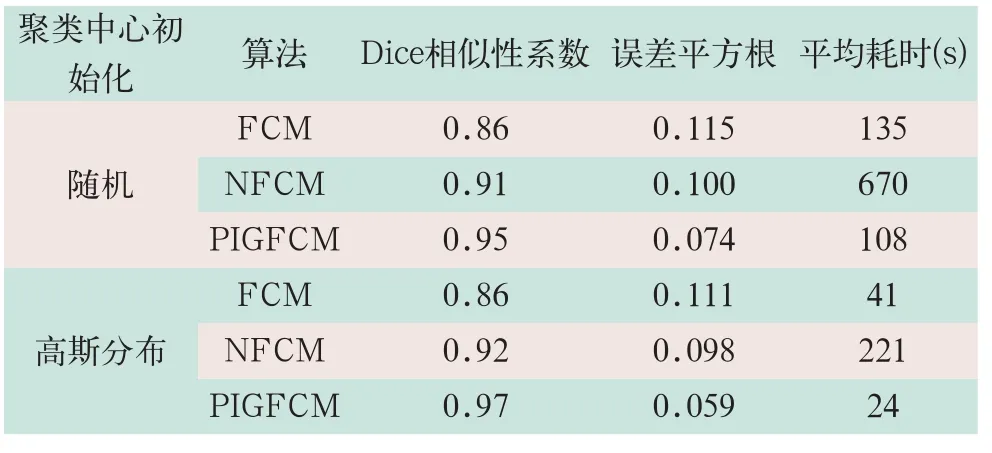
表2 不同聚类中心初始化方法对应的Dice相似性系数、误差平方根和平均耗时
2.2 临床实例MR图像定量分析
采用20幅MR临床实例脑图像进行仿真实验,尺寸为256×256×Z,Z取值范围55~67,层厚3.1 mm,各组织参考体积由两位高年资影像医师勾画获取,各组织初始聚类中心由高斯分布从10幅MR图像训练获得。不同分割算法对应的临床实例图像分割结果见图2。

表1 不同分割算法和噪声水平对应的平均Dice相似性系数
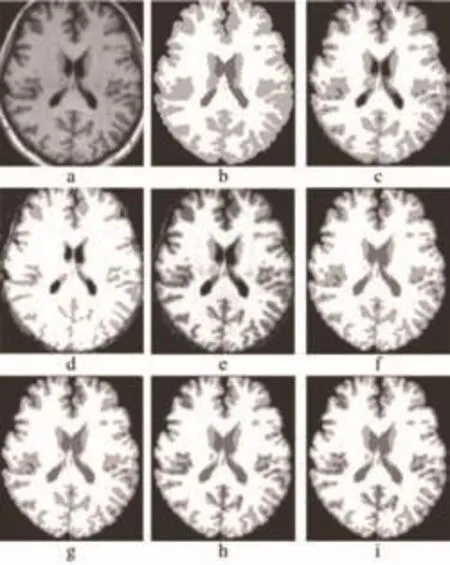
图2 不同分割算法对应的临床实例图像分割
图2显示,基于本研究算法分割的MR图像各组织区域最接近参考图像,其他算法存在过度分割或者分割不足。基于本研究提出PIGFCM分割算法所得脑白质与灰质的Dice相似性系数分别提升12.8%~16.6%和1.1%~40.4%。白质和灰质的RMSE为其他算法的0.63~0.94倍,平均耗时是其他算法的0.08~0.75倍,适用于临床实例MR图像各组织部分分割。不同分割算法对应的临床实例图像分割定量评估结果见表3。
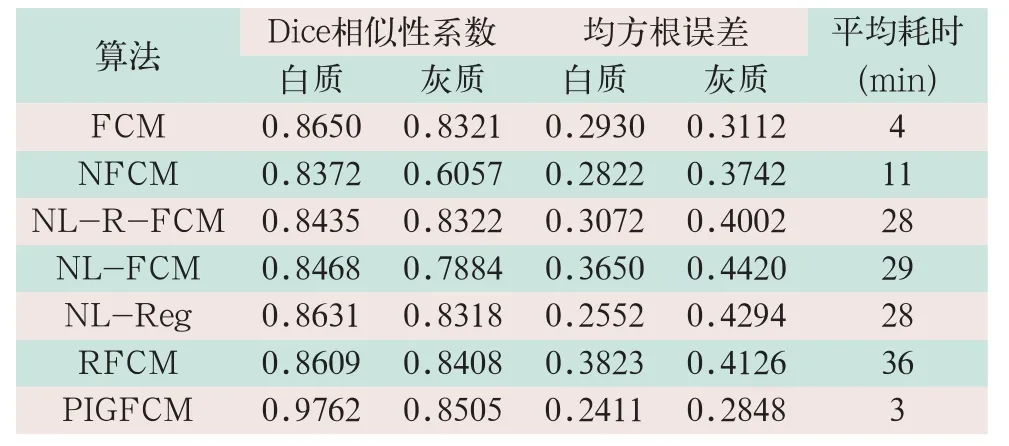
表3 不同分割算法对应的临床实例图像分割定量评估结果
3 结论
本研究提出了一种改进FCM的脑部MR图像分割的PIGFCM聚类算法,主要借助基于高斯分布的图像先验知识获取初始聚类中心,避免初始聚类中心的盲目性,达到快速收敛的作用;然后,采用改进的FCM聚类算法分割脑部MR图像脑白质、灰质和脑脊液区域,得到分割图像。由人工合成和临床实例MR脑部图像分割实验结果可知,基于本研究提出的PIGFCM算法所得脑部各组织区域分割完整,且定量评价指标Dice相似性系数、RMSE和平均耗时均优于其他算法,表明本研究提出的PIGFCM分割算法的精确性、实用性和普适性均较强,适用于脑部MR图像分割。
