拼接镜面主动控制系统的定标*

王 斌，戴懿纯，许方宇，金振宇，杨德华

(1. 中国科学院云南天文台，云南 昆明 650011；2. 中国科学院大学，北京 100049;3. 南京航空航天大学，江苏 南京 211106)

8 m环形太阳望远镜(Ring Solar Telescope)是中国巨型太阳望远镜(Chinese Giant Solar Telescope, CGST)计划的重要方案。8 m环形太阳望远镜计划采用24块面积约为1 m2的等腰梯形子镜拼接，采用主动光学技术实现主镜的共相[1]。由于环形拼接形式的特殊性，8 m环形太阳望远镜在子镜边缘探测的基础上要增加对子镜倾斜量的探测才能实现主动光学的闭环控制[2]，即通过边缘探测器探测子镜边缘高度差的变化，倾斜测量探测子镜倾斜的变化量，从而反演子镜位置的变化，并通过子镜背面的位移促动器对子镜的姿态进行调节，实现主镜的面形保持。

8 m环形太阳望远镜拼接镜面主动光学的控制性能主要取决于倾斜测量的精度与控制模型建立的准确程度。文[2-3]指出子镜倾斜测量对环形拼接镜面主动控制的重要作用，以及8 m环形太阳望远镜要实现衍射极限成像的主动面形控制精度需要的倾斜测量精度。理论的控制模型依赖于促动器与传感器的几何排布关系，主要描述传感器对促动器的响应情况。但是，由于促动器与传感器的安装误差以及在不同环境中传感器和促动器的增益变化，这些因素引起实际控制模型与理论控制模型出现偏差和模型的不确定性，影响控制系统的稳定性，导致控制性能下降[4]。为了获得稳定有效的闭环控制，并对面形控制精度进行充分评估，需要定期对主动光学系统中的测量器件和控制模型进行定标。

围绕8 m环形太阳望远镜主动光学关键技术研究的两镜系统主动光学平台，为了实现主动光学的闭环控制，在相邻子镜边缘探测的基础上，在子镜边缘增加了夏克-哈特曼(Shack-Hartmann, S-H)波前探测器用于子镜倾斜的实时探测。为此，利用泰曼-格林型4D干涉仪和子镜上安装的边缘传感器对子镜边缘的夏克-哈特曼倾斜测量系统进行了交叉定标，对测量精度进行了定量评估，在此基础上，对包括边缘传感器和倾斜传感器的两镜系统主动控制模型进行测量和定标，为两镜系统主动光学闭环实验，后续8 m环形太阳望远镜高精度倾斜测量技术和闭环控制技术的研制和实现提供参考。

1 两镜主动光学系统的介绍

如图1，两镜主动光学系统的控制对象是由两块直径300 mm、边缘厚度大约40 mm的半圆形子镜拼接而成的球面反射镜，曲率半径为2 000 mm。其中一块固定不动，称之为固定子镜；另一块子镜作相对3个自由度的主动位移(piston、 tip/tilt)，称之为主动子镜。系统搭建在光学平台上，光轴水平放置。

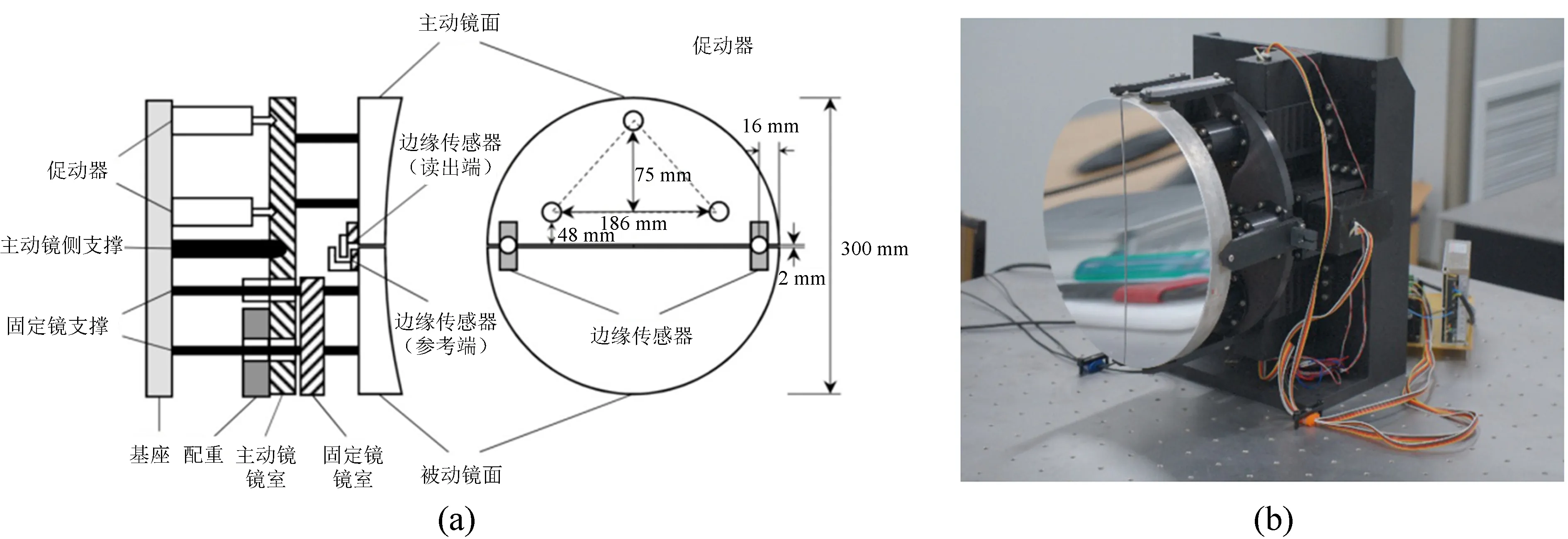
图1 两块拼接子镜示意图。(a) 设计参数；(b) 实物照片
Fig.1 Schematic diagram of the 2-segment mirror. (a) Design parameters; (b) Photograph of the segmented mirror

两镜主动光学系统的执行机构是位于主动子镜背部的3个位移促动器，呈等腰三角形分布。促动器一端固定在基座上，另一端与主动子镜的镜室连接，位移促动器的执行量产生轴向位移，从而实现控制3个自由度的目的。促动器的行程范围 ± 5 mm，可实现5 nm分辨率的轴向位移。

两镜主动光学系统的测量器件包括两部分：

(1)边缘传感器，用于子镜边缘高度的测量。边缘传感器采购德国PI公司的单极电容位移传感器及其采集系统(D-E30.100型单极电容传感器、E-E12.009型模块化数字机箱、中央处理单元及附件)，动态范围 ± 100 μm，动态分辨率为2 nm，安装在子镜背后的拼缝上。

(2)夏克-哈特曼测量系统，用于子镜倾斜的测量[5]。夏克-哈特曼测量系统的核心是微透镜阵列和CCD，整个测量光路如图2(a)。测量系统采用5 × 5的微透镜阵列置于出瞳处，如图2(b)。两子镜的拼缝对准最中间一列子孔径。拼缝左侧的两列子孔径用于参考镜倾斜的探测，右侧两列子孔径用于主动镜倾斜的探测。中间一列子孔径可用于子镜间平移探测。表1给出了夏克-哈特曼倾斜测量系统的基本参数。

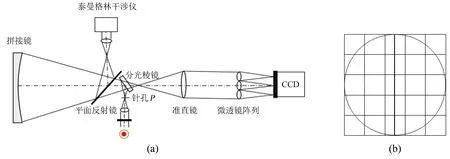
图2(a) 夏克-哈特曼测量系统光路；(b) 子镜与微透镜子孔径对应图
Fig.2(a) The experimental system of S-H sensor; (b) The S-H lens corresponds to sub-segments

表1 夏克-哈特曼测量系统参数Table 1 The parameters of the S-H measuring system

2 夏克-哈特曼倾斜测量系统的精度定标

在两镜主动控制系统中，对夏克-哈特曼探测器倾斜测量的精度进行定标能够为主动控制实施的可能性、最终的面形控制精度以及高精度实时倾斜探测的研制提供评估依据，同时也是建立准确控制模型的基础。在两镜主动控制系统中，对夏克-哈特曼进行定标首先要解决的问题是 “已知像差” 或者 “基准量” 的选取。在这里定义子镜绕y轴的倾斜为Xtilt，绕x轴的倾斜为Ytilt，由于子镜拼缝上安装了两个边缘传感器，当子镜具有一定的Ytilt时，两个边缘传感器的读数将发生变化，并且由于边缘传感器具有很高的动态分辨率，因此可以利用两个边缘传感器读数的差值作为已知基准量对夏克-哈特曼的倾斜测量值进行标定。同时，为了验证定标的精度，在夏克-哈特曼测量光路分光棱镜的前端，还引入了泰曼-格林型的4D干涉仪(PhaseCam@6000，测量精度达到0.000 12λ，λ@ 632.8 nm)，如图2(a)，平面反射镜用于4D干涉仪和夏克-哈特曼探测器的切换。采用交叉定标的方式标定夏克-哈特曼倾斜探测的线性度和重复精度。由于两个边缘传感器只能反映子镜Ytilt的变化，不能反映子镜Xtilt的变化，而夏克-哈特曼探测器对两个方向倾斜探测算法相同，因此可以通过子镜Ytilt倾斜测量的定标精度估算Xtilt倾斜测量的精度。

具体的交叉定标方案为：以一定的步长移动位移促动器，即改变子镜的Ytilt，记录两个边缘传感器的读数差S作为基准量，分别用4D干涉仪和夏克-哈特曼探测器对子镜的倾斜进行测量，为了平滑大气湍流以及局部温度对倾斜探测的影响[6]，4D干涉仪采用32帧测量数据进行积分，夏克-哈特曼探测器采用50帧[7]。图3是子镜的Ytilt连续改变10次，边缘传感器读数差与4D干涉仪倾斜测量值的对应关系；图4是子镜的Ytilt连续改变10次，边缘传感器读数差与夏克-哈特曼倾斜测量值的对应关系。以边缘传感器读数差S为自变量，对上述测量数据按(1)式进行最小二乘拟合：

f(x)=p1x+p2.

(1)

图3的拟合参数为：p1=0.000 804 arcsec/nm，p2=-0.010 3 arcsec，均方根误差(RMSE)为0.013 46 arcsec；图4的拟合参数为：p1=0.000 806 7 arcsec/nm，p2=-0.009 27 arcsec，均方根误差(RMSE)为0.016 97 arcsec。

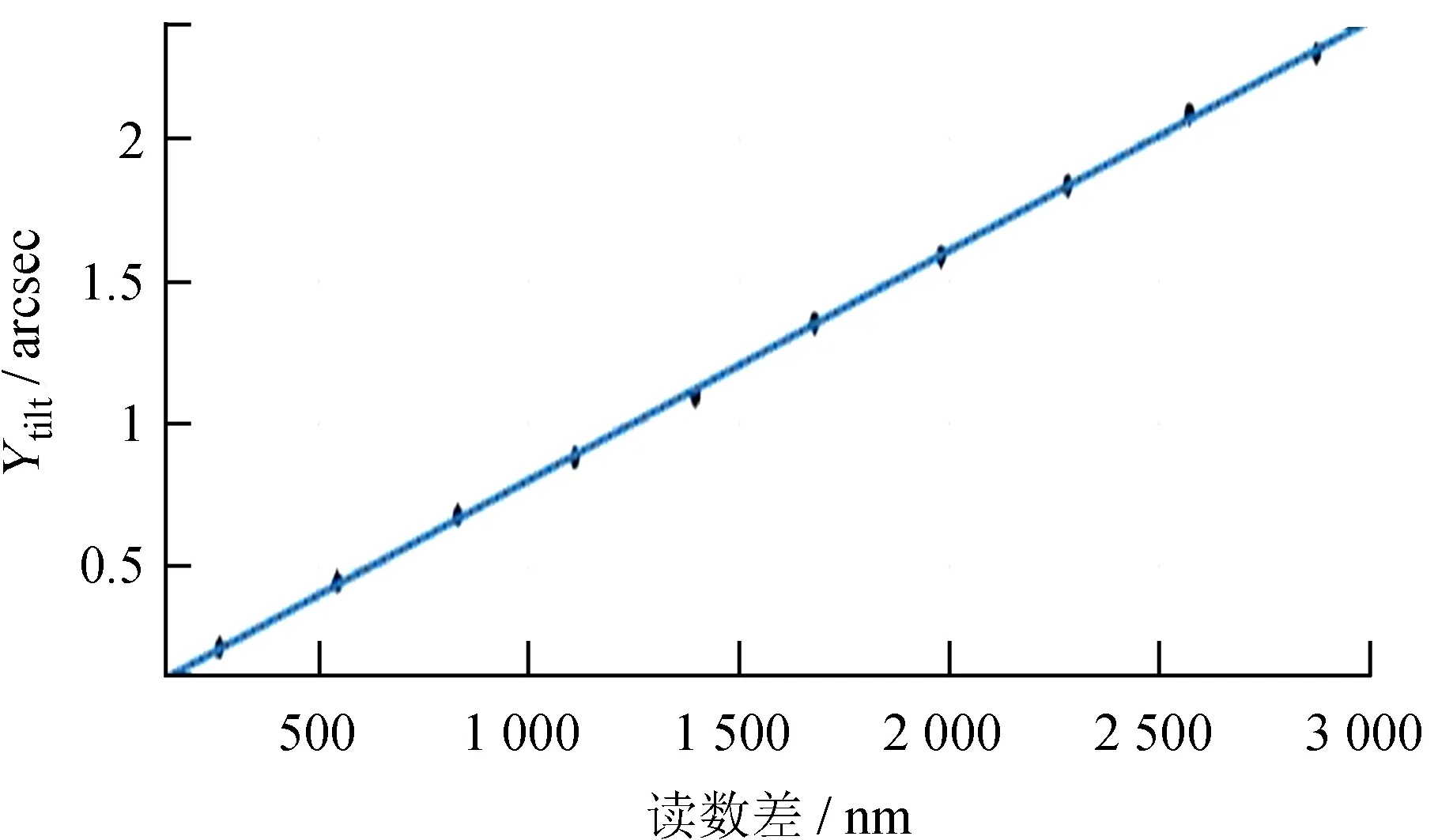
图3 边缘传感器读数差与4D干涉仪测量的Ytilt拟合直线

Fig.3 The fitting line between the numeric difference of edge sensor andYtiltof 4D interferometer

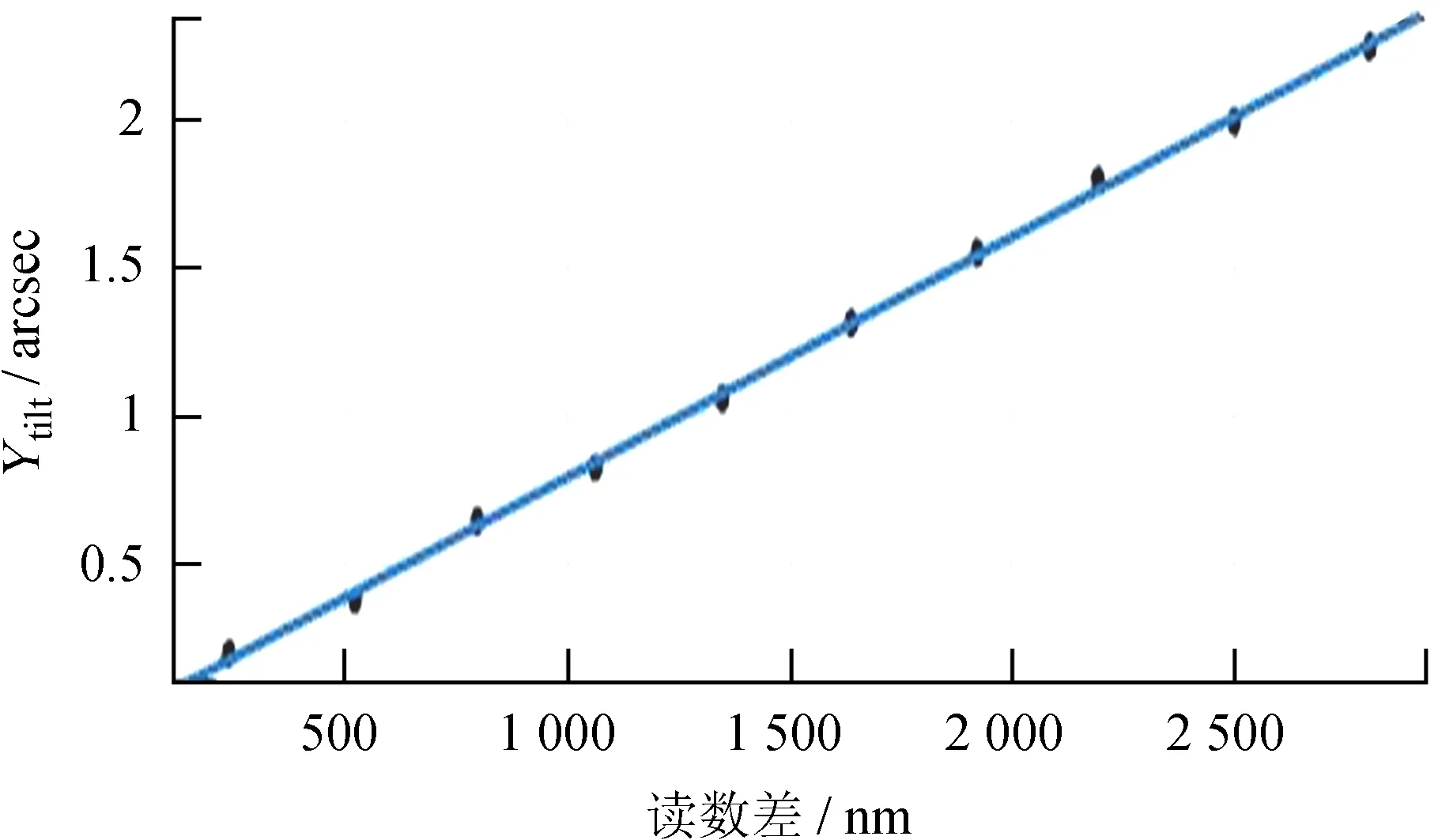
图4 边缘传感器读数差与夏克-哈特曼探测器测量的Ytilt拟合直线

Fig.4 The fitting line between the numeric difference of edge sensor andYtiltof S-H sensor

分别采集8组测量数据，对每组数据进行线性拟合，8组数据拟合参数的均值和标准差如表2、表3。

表2 边缘传感器读数差与4D干涉仪Ytilt测量值的拟合参数

Table 2 The fitting parameters between the numericdifference of edge sensor andYtiltof 4Dinterferometer

p1/(arcsec/nm)p2/arcsecRMSE/arcsec均值8.017×10-40.01120.0117标准差7.496×10-60.01390.0029

表3 边缘传感器读数差与夏克-哈特曼探测器Ytilt测量值的拟合参数

Table 3 The fitting parameters between the numericdifference of edge sensor andYtiltof S-Hsensor

p1/(arcsec/nm)p2/arcsecRMSE/arcsec均值8.064×10-40.00610.0144标准差3.829×10-60.0120.002

从拟合的结果看，夏克-哈特曼测量的重复线性度非常好，与4D干涉仪的测量结果也非常近似。在目前的实验条件下，夏克-哈特曼重复测量精度达到了0.014 arcsec，此测量精度与两镜系统位移促动器的执行精度相匹配。

3 两镜系统主动控制模型的实测定标

3.1 理论的主动控制模型

两镜系统的主动控制模型在传感器和促动器的线性范围内可以表示为

ym=Ax+n，

(2)

其中，ym为探测向量，由边缘传感器测量值和倾斜传感器测量值共同组成；x为位移促动器的执行量；n为探测噪声；矩阵A为控制矩阵，反应了位移促动器和传感器之间的几何对应关系[8]。

根据图5的几何排布形式，当促动器M1有变化量Δm时，整个子镜会以促动器M2和M3的连线为轴旋转，每个边缘传感器的变化量为

(3)

其中，r为边缘传感器到旋转轴的垂直距离；h为促动器到旋转轴的垂直距离[9]。根据(3)式，可以列出子镜上每个边缘传感器的变化量与促动器变化的关系：

(4)

(5)

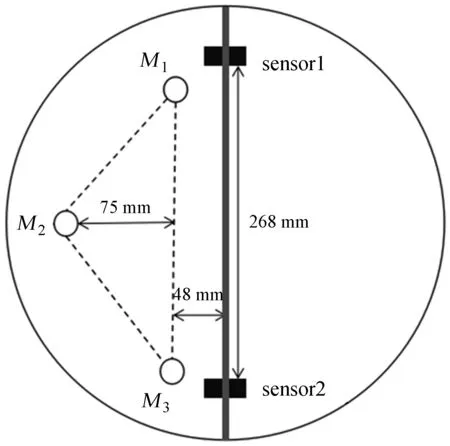
图5 子镜促动器与边缘传感器几何排布情况
Fig.5 Geometric arrangement of actuator and edge sensor

而子镜自身绕y、x轴的倾斜变化用位移促动器的变化可以表示为

(6)

Ty=Δm1-Δm3.

(7)

为了将其与边缘探测统一，需要将(6)式和(7)式转换成子镜边缘高度的变化，Tx,Ty分别乘以各自的边缘高度转换系数, 即Δstx=atxTx，Δsty=atyTy。从而，两镜系统的主动控制模型为

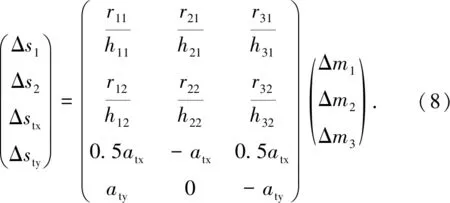
3.2 实测的主动控制模型

利用边缘传感器和倾斜传感器对位移促动器的实际响应，对两镜系统的主动控制矩阵进行定标。根据(8)式前两行，通过促动器的执行量和实测的边缘传感器变化，求取相应的响应系数。测量方法：首先固定促动器M2和M3不动，M1一次执行10步，执行后记录边缘传感器1和2的变化量，重复执行25次； 接着M2和M3也分别重复上述操作，并记录边缘传感器的变化量。促动器变化引起的边缘高度变化的均值与标准差如表4。

根据(8)式后两行，通过促动器的执行量和实测的子镜倾斜量，求取相应的倾斜响应的转换系数。测量方法：固定促动器M1和M3，促动器M2一次执行20步，执行后记录夏克-哈特曼探测器Xtilt测量值，重复执行45次；固定促动器M2，促动器M1一次执行20步，促动器M3一次执行-20步，执行后记录夏克-哈特曼探测器Ytilt测量值，重复测量45次。子镜Xtilt和Ytilt探测的均值和标准差如表5。根据上述实测探测器响应得到的控制矩阵为

表4 促动器执行引起边缘传感器的变化Table 4 Change of edge sensor caused by actuator execution

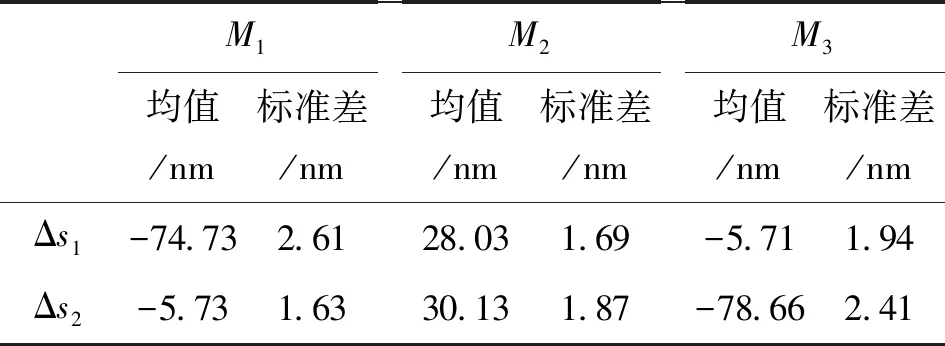
M1均值/nm标准差/nmM2均值/nm标准差/nmM3均值/nm标准差/nmΔs1-74.73 2.61 28.031.69 -5.711.94 Δs2-5.73 1.63 30.131.87 -78.662.41

表5 促动器执行引起夏克-哈特曼传感器的变化

Table 5 Change of S-H sensor causedby actuator execution

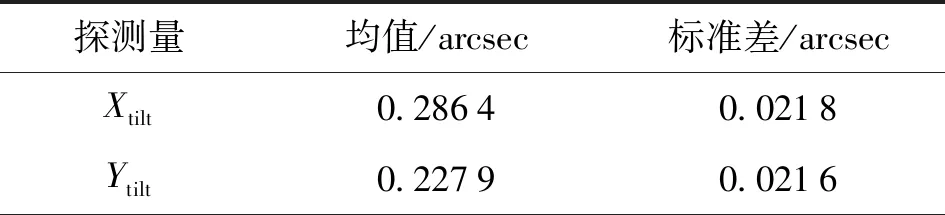
探测量均值/arcsec标准差/arcsecXtilt0.28640.0218Ytilt0.22790.0216

实测的主动控制矩阵与理论的控制矩阵存在明显的偏差，偏差项最大可达14.16%。事实上在动镜系统理论的设计方案中，促动器M1和M3的位置关于半圆对称，而两个边缘传感器的安装位置在半圆子镜的边缘也对称，因此当促动器M1和M3执行相反方向的相同位移量，两个边缘传感器的变化量相同，方向相反。但是经过测量发现边缘传感器1的变化量始终小于边缘传感器2的变化量，这说明促动器和边缘传感器之间存在一定的安装误差，这种安装误差连同促动器的执行误差导致边缘传感器的实际响应以及倾斜探测的实际边缘高度转换系数与理论值的偏差，从而造成实际控制矩阵偏离理论控制矩阵。

4 讨论和结论

本文利用4D干涉仪和子镜的边缘传感器对两镜系统的夏克-哈特曼倾斜探测器的倾斜测量线性度和重复测量精度进行了定标，其重复测量精度达到0.014 arcsec。这种精度接近8 m环形太阳望远镜实现在1 μm波长衍射极限的面形控制要求，但是目前的测量精度是在实验室内大气条件较为平稳的情况下获得的，在具有明显湍流影响下的倾斜测量精度还需要进一步实验确认，而本文采用的交叉定标方法可以用于不同实施条件下夏克-哈特曼倾斜探测和其他倾斜测量方案精度的定标。

本文利用边缘传感器和夏克-哈特曼倾斜探测器实测了两镜主动控制系统的控制矩阵，由于促动器和传感器的安装误差，实测控制矩阵与理论控制矩阵存在明显差异，后续将结合主动控制系统的闭环实验研究控制矩阵差异对主动控制性能的影响，从而对促动器和传感器的安装误差容限提出要求。文中所述的定标主要用于标定由于传感器和促动器安装误差导致的准静态的主动控制矩阵误差。定期对控制矩阵进行实测定标是解决控制矩阵误差随机性的一个可能方案，在后续的工作中进一步分析和分解误差的来源，研究合理的定标周期。