基于样条函数的恒星光谱自动归一化方法*

罗 锋，刘 超，赵永恒

(1. 中国科学院国家天文台，北京 100101；2. 中国科学院大学，北京 100049)

作为国家重大科学工程，大天区面积多目标光纤光谱天文望远镜(the Large Sky Area Multi-Object Fiber Spectroscopic Telescope, LAMOST, 又叫郭守敬望远镜)突破了天文望远镜大视场与大口径难以兼得的难题[1]，成为目前国际上口径最大的大视场望远镜，是我国光学望远镜研制的又一里程碑。截至2018年6月，郭守敬望远镜完成了7年的巡天观测，获取的光谱数首次超过千万量级，成为世界上第一个获取光谱数超千万的巡天项目。遗憾的是，对于这107条光谱，目前没有自动化方法应用到归一化上，本文主要对这方面进行研究。

每条观测谱都由连续谱、谱线和噪声组成[2]。通过谱线可以对恒星的化学组成进行分析，并且由于多普勒效应，谱线还携带着视向速度的信息[3]。因此，从原始光谱中准确地提取谱线是恒星光谱研究及光谱数据处理工作的重要步骤，对后续的研究有重要意义。

要消除连续谱首先要对连续谱进行拟合，目前连续谱拟合方法主要有多项式拟合、中值滤波、小波滤波、形态滤波器等[4]。此外，利用天文软件[5]进行半自动化处理的方法是人工筛选提取认为合适的数据点[6]并选择函数形式，然后由软件进行多项式拟合得到连续谱。这种方法依赖人工参与，无法满足目前巡天项目中海量光谱的实时处理需求。国外的斯隆数字巡天(Sloan Digital Sky Survey, SDSS)中的数据处理程序SSPP(Segue Stellar Parameter Pipeline)采用分段多项式拟合的方法[7]：首先将光谱分为红端和蓝端两部分，去除强巴尔末线系后，分别对蓝端使用9阶、红端使用4阶多项式分别拟合，丢弃3个标准差以外的数据点；然后拼接两段连续谱再进行一次9阶多项式拟合，得到最终的连续谱。这种方法稍显繁琐，且计算量大。

本文提出的方法是将光谱划分为数个固定的(包含相同的像素数量)窗口，窗口内选中值点，通过筛选策略丢弃部分参考点，这样做能够有效地避开发射线、吸收线及宇宙线的干扰。通过对参考点之间 “夹角” 的控制，使用非常小的平滑度构造样条曲线，实现对连续谱的精确拟合。

1 方法介绍

本文提出的连续谱归一化方法包含3个步骤：(1)将一条待处理光谱根据数据点总数划分为数个窗口，每个窗口选出流量中值点形成参考点集；(2)制定一些筛选策略，将参考点集中有可能影响拟合结果的数据点丢弃；(3)根据参考点流量最大值所在波长位置选取对应的样条函数平滑度经验值进行拟合，得到连续谱。

1.1 划分窗口构造参考点集

为了有足够的数据点作为拟合函数的控制点，根据输入的待处理光谱数据点总数，采用如表1的策略划分窗口。设数据点总数为n，每个窗口包含像素数，即窗宽为w。

表1 窗宽与数据点总数之间的对应关系Table 1 The relationship between windows width and the total number of data points

根据表1确定窗宽后对光谱进行窗口划分，遍历所有窗口，每个窗口内选取流量值等于窗口中所有点中值的像素作为参考点，并将其加入参考点集Srp。

1.2 筛选参考点

1.1节中构造的参考点集Srp只体现了光谱的大致形状，其中有些点可能位于吸收线或者发射线上，如图1、图2。

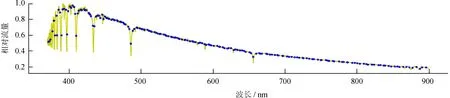
图1 有些参考点位于吸收线上
Fig.1 Some reference points are on the absorption line

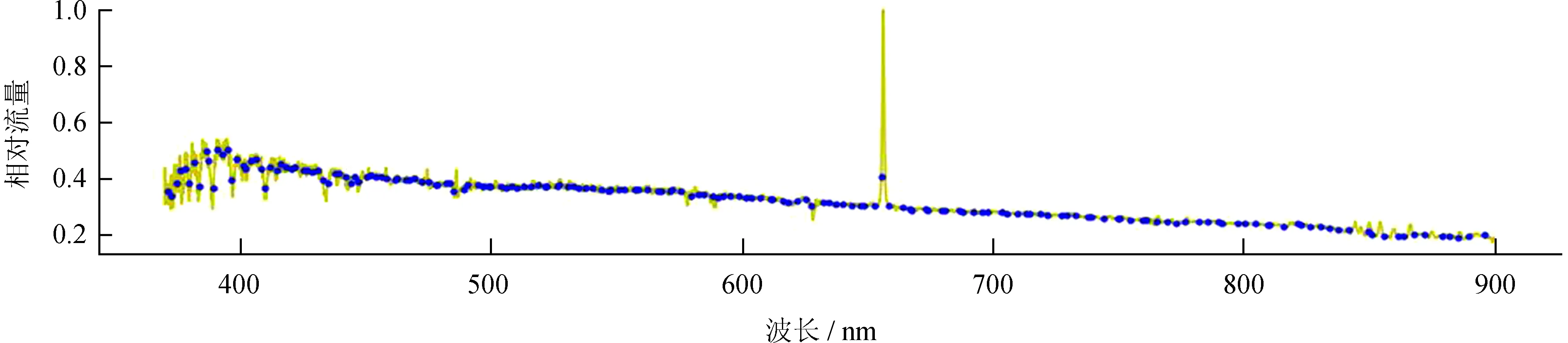
图2 有些参考点位于发射线上
Fig.2 Some reference points are on the emission line

理论上，连续谱应非常接近黑体辐射谱，而黑体谱可以划分为两个单调区间，峰值左边是单调增区间，右边是单调减区间[8]，希望用来构造拟合曲线的参考点符合并体现这一特征。为了实现这一目标，采取两个步骤对参考点集再次筛选。

(1)丢弃局部极小值点

设Srp中一个参考点的索引为i，流量为f(i)，若i满足：

f(i-1)>f(i)并且f(i)

(1)

则将参考点i从Srp中删去。每次从i=1开始到遍历完Srp中所有参考点结束为一趟，在一趟丢弃结束时，有些点可能成为新的局部极小值点，此时需要再丢弃一趟。设丢弃的趟数为t，需要保证以下两点：(1)对连续谱正常的光谱，t次丢弃之内Srp中元素数量不再减少；(2)对连续谱异常[9]的光谱，t次丢弃后Srp中有足够的参考点用来构造拟合曲线。实验表明，合适的t取值为t=len(Srp)//30 + 2。

经这一步骤处理后，图1和图2中两条光谱的参考点集如图3、图4。

图3 图1中光谱经t次丢弃局部极小值后的参考点集
Fig.3 The reference point set after the local minimum is discardedttimes in the spectrum in Fig.1

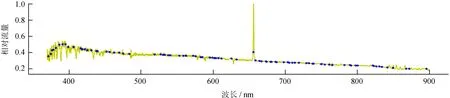
图4 图2中光谱经t次丢弃局部极小值后的参考点集
Fig.4 The reference point set after the local minimum is discardedttimes in the spectrum in Fig.2

(2)丢弃 “夹角” 较大的点

为了获得更加精确的连续谱拟合曲线，需要较小的平滑度构造样条函数。如果有的参考点和其左右两点连线构成的夹角过大，则会给拟合曲线带来较大的偏离，这样的参考点应从Srp中删去，如图5。

图5 位于发射线上的数据点应从参考点集中删去
Fig.5 The data point on the emission line should be removed from the reference point set

如图6，在参考点集中取一点i，设其对应的波长为w(i)，流量为f(i)，与它左右两点间连线的夹角为θ(i)，组成的三角形边长分别为a,b,c。在几何上，有：

(2)

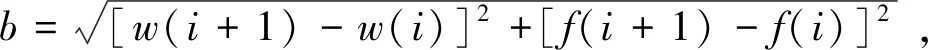
(3)

(4)

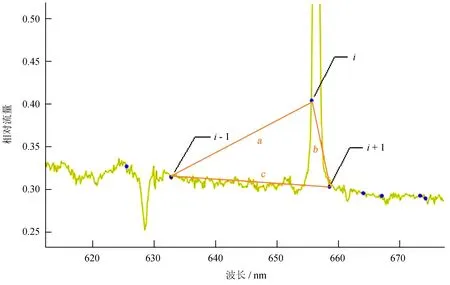
图6 使用余弦定理计算 “夹角”
Fig.6 Calculate the angle by use of Cosine theorem

根据余弦定理计算θ(i)的值。实际上，流量值并不对应长度单位，w和f的单位很难统一。由于光谱数据中流量是未定标的相对流量，直接用余弦定理计算的夹角随着光谱流量值所在的区间不同及光谱数据处理中必要的乘除运算而变化。为此做如下处理：

对于Srp中的一个参考点i，设其与左边数据点波长数值的差为wd-，右边为wd+，则：

wd-=w(i)-w(i-1)，

(5)

wd+=w(i+1)-w(i) .

(6)

同理，对于流量值[2]：

fd-=f(i)-f(i-1),

(7)

fd+=f(i+1)-f(i) .

(8)

引入比例因子rw,rf，令：

(9)

(10)

计算判据r=|rw-rf|的值并引入阈值r0。若r>r0，则认为点i属于夹角较大的点，会给精确拟合带来干扰，应从Srp中除去。通过实验发现，效果较好的r0取值为0.5。

通过比值消去量纲，则不论w与f取何种单位，rw,rf都是不变的。使用rw,rf作为判断依据寻找这样的参考点更为可靠。图5中光谱经此步骤处理后的结果如图7。

图7 位于发射线上的参考点被成功移除
Fig.7 The reference point on the emission line was successfully removed

1.3 平滑度计算

样条函数[10]拟合效果的好坏，除了与参考点的选取有关，还取决于平滑度的选择。对于同一条光谱，同样的参考点集，不同的平滑度会有不同的效果，如图8。

图8 平滑度对拟合曲线的影响
Fig.8 The influence of smoothing factor on fitting curve

较小的平滑度可以更好地照顾到光谱图像上起伏的细节，但过小容易产生振动频繁的现象，使拟合曲线无法体现连续谱；较大的平滑度不会有剧烈的振动，但是过大会使拟合曲线过于平缓，也无法很好地体现连续谱。应该指出的是，对于同一个平滑度，在不同的流量区间，样条曲线会有不同的表现。在拟合之前，将光谱数据进行最大值标准化，即flux=flux/max(flux)。

经实验分析，温度越高的光谱需要越小的平滑度照顾光谱在蓝端较急剧的转折，温度越低的光谱需要越大的平滑度弱化参考点上下起伏的趋势。而一条光谱的温度在连续谱上体现为流量峰值所在的位置。采用在参考点集中选取流量最大值，用其所在波长位置估计该条光谱的温度区间，选择对应的平滑度s0。为了能够适用于局部归一化的场合，对于参考点较少的情况，需要更小的平滑度。为此，引入默认值为1的比例系数c，用于在参考点较少时将之与s0相乘的结果作为最终的平滑度取值。具体数据列在表2和表3中。

在构造样条曲线时使用的平滑度为：

s=c*s0.

(11)

表2 根据参考点集中流量最大值点所在波长位置选择平滑度

Table 2 Selection of smoothing factor according to the wavelength positionof the maximum flux point in the reference point set

wave/nm370～476476～688688～794794～900s00.010.020.030.05

表3 根据参考点集中数据点数n选择平滑度比例系数c

Table3Selectionofproportionalitycoefficientcofsmoothingfactoraccordingtothenumberofdatapointsninthereferencepointset

n1～2930～5960～8990～119120～149150～180c0.20.350.50.650.81

2 实验结果

2.1 不同情况下的处理结果

为检验所提出方法的处理效果，从郭守敬望远镜中随机抽取了不同类型的光谱10 000条进行实验。从中选出不同温度的光谱进行拟合，如图9。图中左侧蓝色实线为原始光谱，红色实线为拟合曲线；右侧绿色实线为对应的归一化谱。由图9可见，本方法在不同温度时做到了较好的拟合。

如图10，左侧桃红色实线是原始光谱，绿色实线为样条函数拟合曲线；右侧靛蓝色实线为对应的归一化谱。选取不同的波长覆盖范围后，本方法能够自动应用于需要局部归一化的场合，不需要人工干预。

如图11，左侧是原始光谱及拟合曲线，在不同的信噪比情况下，本方法拟合效果受到的影响不大。与文[11]中专为低质量光谱开发的归一化方法处理效果非常接近。

如图12，在光谱中含有发射线及宇宙线的情况下，本方法仍能有效识别并进行准确的拟合。

2.2 误差分析和适用范围

由于仪器原因，光谱中常见的仪器形变模式有3种，如图13(a)。为了测试本文提出的方法是否能够有效地处理这些仪器导致的光谱形变，在有效温度4 000～8 000 K的范围内随机抽取9条光谱，每条光谱归一化后的结果都乘以这3种形变曲线，并再次归一化。图13(b)的直方图中显示了两次归一化结果残差的分布，可以看出本文算法的误差平均值在10-3量级，误差弥散在10-2量级。

经实验分析，本方法适用条件如下：信噪比范围5～600，波长覆盖范围370～900 nm，有效温度范围3 000～50 000 K。其中，信噪比低于5的光谱处理结果不稳定，总体精度有随着信噪比下降而降低的趋势。有效温度小于3 000 K的光谱处理结果同样不稳定，大量光谱总的结果变得不可信。除此之外，信噪比高于600，波长小于370 nm或大于900 nm，有效温度高于50 000 K的光谱未做实验。另外，本方法适用于中低色散的光谱，高色散光谱需要对参数进行微调。

需要指出，对于本方法涉及的参数w,t,r0,s0,c，它们的选择是为了适应仪器特性，对于其他来源的光谱，该方法仍然可用但参数初值需要略微调整。

图9 不同温度下的归一化结果
Fig.9 Normalization results at different temperatures

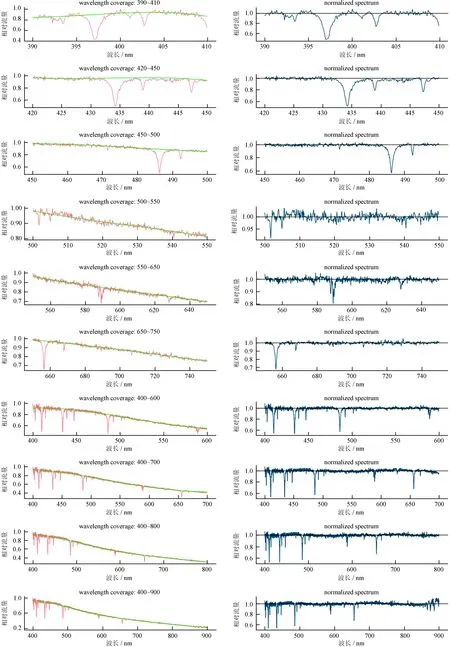
图10 不同波长覆盖范围的归一化结果
Fig.10 Normalization results of different wavelength coverage range

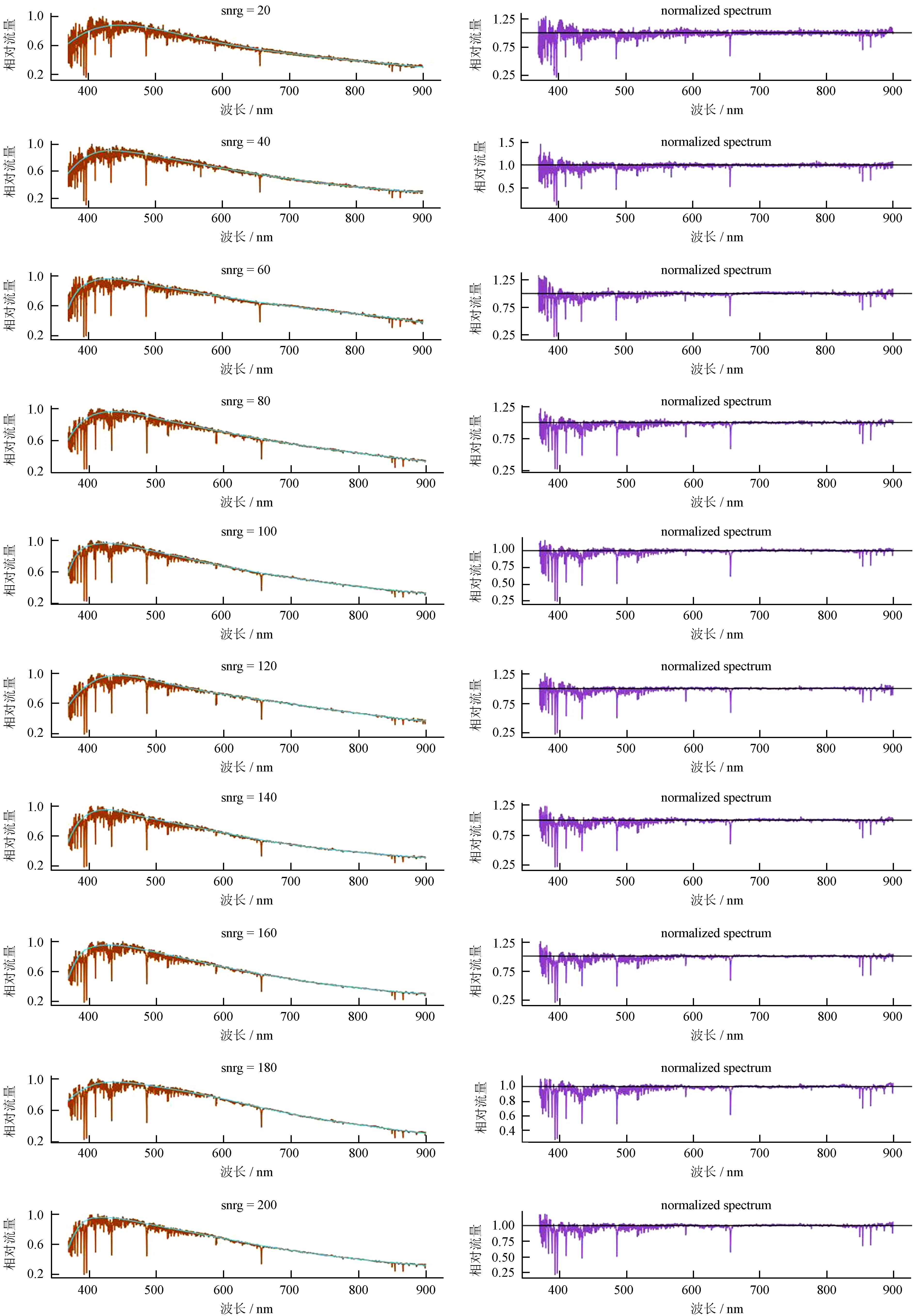
图11 不同信噪比的归一化结果
Fig.11 Normalization results under different SNR

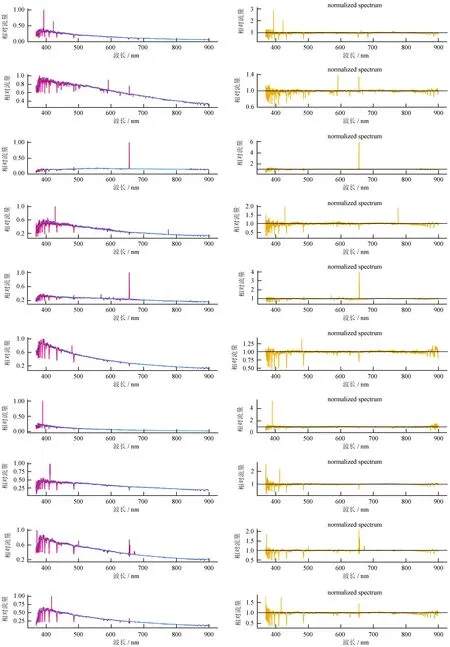
图12 含有发射线或宇宙线情况下的归一化结果
Fig.12 Circumstances containing emission lines or cosmic rays

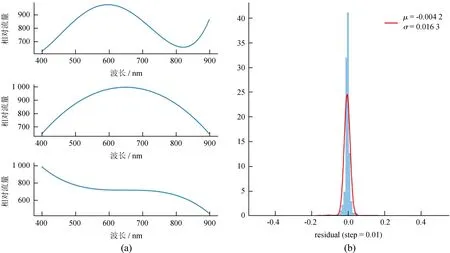
图13 郭守敬望远镜的形变模式及归一化误差分析
Fig.13 Deformation mode in LAMOST and error analysis of normalization

3 结论与展望

归一化是光谱数据处理的重要环节，这一步骤处理结果的准确度直接影响后续数据分析结果的正确性以及精确程度。为了获得更加准确的连续谱，在国内外研究的基础上提出了基于固定窗口划分的样条函数拟合方法，通过大量实验修正其中某些参数的经验取值。随后，利用更多的数据进行验证，结果表明，本方法在拓宽适用范围的前提下实现了自动化处理，与其他方法相比具有更好的普适性，在需要大规模自动化处理的场合有独特的优越性。

恒星光谱的归一化方法有很多种，在不同的场合各有优劣。本文的方法致力于实现郭守敬望远镜海量光谱实时处理的自动化及普适性拓展。涉及到的参数值是在大量实验的基础上，由经验总结出来的。另外，在开发算法的过程中，有一个重要问题未得到很好的解决，即缺乏一个严格的最优解评价标准来衡量归一化结果的好坏，使得算法仅能对一些明显的错误(如连续谱出现负值)做出基本的容错处理。如果能够研究出可量化并且方便计算机实现的归一化结果评价标准，则可以对处理结果进行评价，通过参数自动修改后再次处理直至获得最优解。

随着天文数据的急剧增长，还需要更加高效和智能的归一化方法及数据处理程序。下一步将进行低温星、特殊星(如碳星等)的光谱归一化研究。