利用端点延拓提高LS + NN模型的UT1-UTC预报精度*

赵丹宁，雷 雨,2

(1. 宝鸡文理学院电子电气工程学院，陕西 宝鸡 721013；2. 中国科学院国家授时中心，陕西 西安 710600)

地球自转运动可以用地球定向参数(Earth Orientation Parameters, EOP)表征。地球定向参数包括岁差、章动、UT1-UTC及极移的两个分量xp与yp。地球定向参数是实现地球参考坐标系与天球参考坐标系相互转换的必要参数，在天文地球动力学研究、卫星导航及深空探测与跟踪等领域均有重要作用。甚长干涉基线测量(Very Long Baseline Interferometry, VLBI)和全球卫星导航系统(Global Navigation Satellite System, GNSS)等空间测地技术是测量地球定向参数的主要手段，其中UT1-UTC的测量精度为3～5 μs[1]，但复杂的资料处理过程致使地球定向参数的获取存在一定的延迟。由于深空探测与跟踪等领域对地球定向参数实时观测值有重要需求，而卫星自主导航又对地球定向参数中长期预报值有重要需求，因此对地球定向参数进行高精度的短期与中长期预报具有重要的现实意义。在地球定向参数的几个分量中，UT1-UTC是变化最快、最难精确预报的一个分量。

当前预报UT1-UTC的方法有多种，其中多数方法联合最小二乘(Least-squares, LS)外推和神经网络(Neural Network, NN)或自回归(Autoregressive, AR)等模型进行预报[2-3]。这些方法的思路为，首先采用最小二乘外推模型提取UT1-UTC序列中的周期项，并对周期项进行外推，然后利用神经网络或自回归等模型对最小二乘拟合残差进行建模、预报，最后再将周期项和残差项的外推值相加得到UT1-UTC的预报值。在预报实践中发现，利用最小二乘外推模型对UT1-UTC观测资料进行拟合时，在拟合序列的两端存在发散畸变现象，这种现象在数据处理中称为端部效应[4-5]。端部效应使残差项、周期项的预报值出现偏差，最终导致UT1-UTC的预报值不准确。

本文针对UT1-UTC预报中最小二乘拟合出现的端部畸变现象，在采用最小二乘外推模型对UT1-UTC观测资料进行拟合之前，先利用灰色模型对UT1-UTC观测资料进行数据延拓，即在UT1-UTC序列的两端增加应用灰色模型延拓的若干数据点，形成一个新序列，然后利用最小二乘外推模型对新序列进行拟合，最后再联合最小二乘外推模型和神经网络(LS + NN)对原始UT1-UTC序列外推，这样就可以将最小二乘拟合出现的端部畸变现象移至新序列的两端。数值分析表明，通过在UT1-UTC序列两端增加统计延拓数据，可以有效地抑制最小二乘拟合出现的端部效应现象，并且可以显著提高预报精度。

1 端点延拓算法

灰色模型可以在系统变化规律不明确的情况下利用少量的已知信息推知系统的发展趋势，且预测精度高、建模简单。一方面，灰色模型可以利用较少的观测数据进行UT1-UTC序列的端点外推延拓，所外推的序列在一定程度上反映UT1-UTC序列的整体变化趋势[6]；另一方面，基于端点延拓算法形成的UT1-UTC新序列仅用来求解最小二乘模型系数，目的是将最小二乘拟合出现的端部效应移至新序列的两端，而两端序列并不参与UT1-UTC预报[7]。因此，基于灰色模型的端点延拓算法用于改善最小二乘拟合的端部效应是完全可行的。

灰色模型建模的基本思路为，首先利用少量原始观测值通过累加生成操作(Accumulated Generating Operation, AGO)生成一次累加序列，然后利用此累加序列建立相应的离散预测模型，并获得累加序列的预测值，最后再通过累减生成操作(Inverse Accumulated Generating Operation, IAGO)获得原始序列的预测值。灰色预报模型GM(1, 1)的一般形式：

x^(k+p)=[x(1)-u/a]e-a(k+p-1)(1-ea),

(1)

其中，u，a为灰色模型系数；k为参与建模的原始观测值个数；p为预报跨度。设X={x(1),x(2), …,x(n)}为原始离散序列，则灰色模型端点延拓算法如下：

(1)对于原始离散序列X的左端，在左端点处取k个观测值，其反序列为

X1={x(k),x(k-1),…,x(1)}，

(2)

将X1作为左端建模序列进行灰色预测，得到预测序列：

X2={x^(0),x^(-1),…,x^(1-p)}，

(3)

则X2的反序列，即原始离散序列X的左端点延拓序列为

X3={x^(1-p),x^(2-p),…,x^(0)}.

(4)

(2)对于原始离散序列X的右端，在右端点处取k个观测值，得到序列X4：

X4={x(0)(n-k+1),x(0)(n-k+2),…,x(0)(n)}，

(5)

将X4作为右端建模序列进行灰色预测，得到预测序列：

X5={x^(n+1),x^(n+2),…,x^(n+p)}，

(6)

将序列X3，X5分别作为原始离散序列X的左、右端点延拓值，得到延拓后的离散序列：

X′={x^(1-p),…,x^(0),x(1),…,x(n),x^(n+1),…,x^(n+p)}.

(7)

2 预报模型

2.1 最小二乘外推模型

UT1-UTC序列中的长期趋势项、周年项及半年项利用如下模型进行拟合：

(8)

其中，ω1，ω2分别为周年项和半年项的振荡角频率，取ω1=2π/365.24，ω2=2π/182.62[4]；γ，β，di和ei为未知参数，可通过最小二乘法求解。

2.2 神经网络模型

提取长期趋势项和周期项后的最小二乘拟合残差序列中含有剩余的短周期成分，也含有非线性成分，对于这些成分，利用神经网络进行建模较为合理。对于最小二乘拟合残差序列{ε(t),t=1, 2, …,n}，假设t时刻的残差值ε(t)可由t-1,t-2, …,t-m时刻的历史残差值ε(t-1),ε(t-2), …,ε(t-m)进行预测，可建立从输入模式到输出模式的数据映射f：Rm→R，预测模型可表示为

ε(t)=f([ε(t-1),ε(t-2),…,ε(t-m)])，

(9)

其中，m为嵌入维数。本文采用极限学习机(Extreme Learning Machine, ELM)算法训练神经网络[8]，从而建立从输入模式到输出模式的数据非线性映射。在残差预报过程中，当已经预报出一部分残差值的情况下，后面的残差是根据其对应的历元通过移动窗口的方法获得[9]。

2.3 预报流程

本文模型与常规最小二乘加神经网络模型的差别之处在于，本文模型在对UT1-UTC序列进行最小二乘拟合之前，先应用灰色模型在UT1-UTC序列两端进行数据延拓，然后再对延拓后的UT1-UTC序列进行最小二乘拟合，建立周期项和趋势项最小二乘外推模型，最后利用最小二乘加神经网络模型对原始UT1-UTC序列进行预报。值得说明的是，在对UT1-UTC序列进行外推之前，需要根据国际地球自转与参考系服务(International Earth Rotation and Reference Systems Service, IERS)协议扣除UT1-UTC序列中周期为5 d～18.6 a的62个固体地球带谐潮汐项[10]，同时还必须扣除闰秒。将本文提出的模型称之为端部效应改善的最小二乘加神经网络(Edge-effect Corrected LS + NN，ECLS + NN)模型，预报流程如图1。

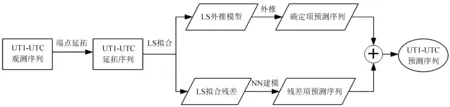
图1 端部效应改善的最小二乘加神经网络模型的预报流程
Fig.1 Flowchart of the ECLS + NN prediction model

3 模型验证

3.1 数据来源

本文试验所用的UT1-UTC数据来自IERS发布的EOP 08 C04序列，时间跨度为2000-01-01～2016-10-01，采样间隔为1 d。

3.2 精度评定标准

为了衡量UT1-UTC预报结果的精度，选用平均绝对误差(Mean Absolute Error, MAE)作为精度评定标准，其计算公式为

(10)

3.3 结果分析

选取2001-01-01～2016-09-20期间的UT1-UTC观测资料进行试验分析，其中2010-01-01～2016-09-20为预测期，建模数据长度为10 a，每隔7 d预报1次，总共进行了300次预测。

为了验证端点延拓方法对最小二乘拟合端部效应的改善效果，首先对比端点延拓前后最小二乘拟合效果。图2分别绘出了端点数据延拓前后最小二乘拟合序列左、右端360个历元的拟合残差数据点，拟合时段为2002-01-01～2011-12-31，其中，端点数据延拓个数为240，即在UT1-UTC观测序列的左、右两端各延拓120个数据点。从图2可以看出，与直接对UT1-UTC原始序列进行拟合相比，基于灰色模型端点延拓后的UT1-UTC序列在左、右两端最小二乘拟合的残差值更小，这说明端点延拓方法可以提高最小二乘模型在UT1-UTC序列左、右两端的拟合准确性，从而抑制最小二乘拟合序列出现的端部效应现象。

图2 最小二乘和端部效应改善的最小二乘模型在UT1-UTC序列左、右两端的拟合残差
Fig.2 LS and ECLS fitting residuals of the UT1-UTC time-series at boundaries

为了进一步检验基于灰色模型的端点延拓方法对最小二乘加神经网络模型预报UT1-UTC的改善效果，本文分别利用最小二乘加神经网络模型与端部效应改善的最小二乘加神经网络模型对UT1-UTC进行1～300 d的预报，图3绘出了最小二乘加神经网络模型和端部效应改善的最小二乘加神经网络模型UT1-UTC预报结果的平均绝对误差曲线，表1统计了最小二乘加神经网络模型和端部效应改善的最小二乘加神经网络模型在不同预报长度下的平均绝对误差值。从图3与表1可以发现，端部效应改善的最小二乘加神经网络模型相对于最小二乘加神经网络模型的UT1-UTC预报精度在各个跨度都有不同程度的提高，其中，对于跨度为1～90 d的预报，精度提高在10%以内；从第90 d开始，端部效应改善的最小二乘加神经网络模型的预报精度提高越来越显著，最大提高达40%，这说明端部效应改善的最小二乘加神经网络模型对于UT1-UTC中长期预报精度改进更为显著。

表1 最小二乘加神经网络模型和端部效应改善的最小二乘加神经网络模型不同跨度UT1-UTC预报结果的平均绝对误差统计

Table 1 MAE statistics of the UT1-UTC predictions by the LS + NN and ECLS + NN models

跨度/dLS+NN/msECLS+NN/ms精度改善百分比/%10.0880.081850.3990.3941100.9620.9521202.2142.1991303.4753.3444606.4276.19049010.6959.5831012017.06712.8222518029.34423.9251824040.91526.6173527048.38428.8664030054.35933.40839

图3 最小二乘加神经网络模型和端部效应改善的最小二乘加神经网络模型UT1-UTC预报结果的平均绝对误差比较

Fig.3 MAE comparison between the LS + NN and ECLS + NN models for the UT1-UTC predictions

4 结果分析

本文提出了一种利用端点延拓改善最小二乘拟合序列端部效应的方法，该方法在对UT1-UTC序列进行最小二乘拟合之前，首先在UT1-UTC序列两端增加统计延拓数据，然后再对数据延拓后的新序列进行最小二乘拟合，目的是将最小二乘拟合存在的端部畸变移至新序列的两端，从而抑制原始拟合序列的端部畸变。试验结果表明，通过在UT1-UTC观测序列的两端增加用灰色模型延拓出的外推数据点，然后再进行最小二乘拟合，能够有效地抑制端部效应的影响。与常规最小二乘加神经网络预报模型相比，端部效应改善的最小二乘加神经网络模型的UT1-UTC预报精度在各种跨度均有不同程度的提高，其中跨度为中长期预报的精度提升尤为明显，因此端部效应改善的最小二乘加神经网络模型更适用于UT1-UTC中长期预报。