基于独立成分分析的射频干扰信号消除方法*
2019-07-16尚振宏徐永华杨亚光强振平
戴 伟,尚振宏,徐永华,刘 辉,杨亚光,强振平
(1. 中国科学院云南天文台,云南 昆明 650011;2. 昆明理工大学信息工程与自动化学院,云南 昆明 650500;3. 昆明理工大学云南省计算机技术应用重点实验室,云南 昆明 650500;4. 中国科学院大学,北京 100049;5. 西南林业大学大数据与智能工程学院,云南 昆明 650224)
射电信号正在成为人类研究宇宙的重要窗口[1],尤其是针对脉冲星检测和观测已成为射电天文的重要研究内容。从凝聚态到量子色动力学,以及一系列涵盖恒星演化、星际介质、宇宙学的天体物理学主题,脉冲星提供了不可替代的实验环境[2-3]。通过脉冲星观测直接证实了太阳系外行星的存在[4],为暗物质的本质及分布的研究提供了条件,并首次为引力波的存在提供了间接证据[5]。
然而,射频干扰(Radio Frequency Interference, RFI)成为上述研究的重要挑战[6]。在射电天文中,射频干扰广义上指由人类生产和生活活动产生的无线电信号,包括电视信号、调频无线电传输、全球定位系统(Global Positioning System, GPS)、手机和飞机导航通讯等对接收的微弱天文信号造成的影响[7]。不同来源的射频干扰在时频特性上的差异使得针对所有类型的射频干扰信号进行建模非常困难[7]。为减少射频干扰,射电望远镜在选址时,通常选择没有或者很少受到射频干扰影响的地理环境,并和相关政府部门协调规划出无线电宁静区。但随着射电天文仪器灵敏度不断提升,接收到非天文信号的干扰越来越明显。宽带、广播和通信中频谱的大量使用,以及越来越多的大规模生产、经济和商业活动,低功率人工宽带信号的使用也变得越来越频繁,这些都会产生射电天文数据中很难消除的干扰信号,使已有的射频干扰问题变得愈发严重[8]。例如,云南天文台利用40 m射电望远镜S波段(2 150~2 450 MHz)开展脉冲星观测任务,2006年5月投入运行之初射频干扰相对较少,但由于该望远镜距离昆明市区较近(距离市中心直线距离8.2 km),且随着城市建设不断发展,包括2 G,3 G,4 G手机信号频段和WIFI频段的射频干扰越来越多,这些干扰信号严重影响了日常射电天文观测。例如,图1展示了云南天文台40 m射电望远镜观测到的脉冲星信号,其中除期望的脉冲星信号外,可清楚地观测到射频干扰。射频干扰的来源和射电望远镜运行的机理决定了几乎所有射电望远镜面临射频干扰问题。观测数据的好坏关系到科学成果的质量甚至结论的真伪,开展射频干扰抑制和消除方法研究对射电天文发展具有重要理论意义与实际应用价值。

图1 脉冲星J0332 + 5434频域柱状图
Fig.1 The phase distributions of J0332 + 5434 in frequency domain
射频干扰消除的目的是在尽量保持天文信号的前提下,消除射电干扰。依据射频干扰消除方案,在射电天文的不同观测阶段可分为4个环节[8]:观测站预防、预检测、预相关以及应用于干涉数据的后相关方案。对于已经建好投入使用的射电望远镜,后相关处理尤显关键和重要,本文主要针对该环节研究射频干扰的消除方法。
后相关消除方法是基于统计分析数据准确标记射频干扰,即通过时频二维平面上射频干扰信号与天文信号形态特性的差异标记并消除射频干扰。天文信号通常呈现宽带、平滑且时间跨度大的特点,而射频干扰信号经常在时频平面上呈现为高强度像素。目前的射频干扰消除方法可分为两类:(1)基于阈值的方法,例如累计和方法[9]与阈值求和方法[6]。这类方法把射频干扰定义为在时频平面上超过某些阈值的像素。算法简单高效,被广泛应用于射电数据处理[10]。但此类方法最大的问题在于如何根据射频干扰源及观测天体确定阈值?尤其是脉冲星等时变天体信号,阈值选择尤为关键。例如,在对低频阵列(The LOw-Frequency ARray, LOFAR)的恒星撕裂事件天体Swift J1644 + 57进行研究时,并未检测到预期的源,分析原因可能是其微弱的瞬时信号被认定为射频干扰而删除[11];(2)基于机器学习的方法。近年来,机器学习尤其是深度学习技术在众多领域取得了令人瞩目的研究成果,已有研究将机器学习中的有监督学习以及深度学习的方法应用于射频干扰消除,取得一定的研究进展。例如文[12]基于K近邻(k-Nearest Neighbor)和混合高斯模型(Gaussian Mixture Models)对射频干扰信号进行聚类,从而实现射频干扰标记;文[13]对基于人工神经网络(Artificial Neural Network, ANN)、自适应提升(Adaptive Boosting, AdaBoost)、梯度提升分类器(Gradient Boosting Classifier, GBC)和极值梯度提升(eXtreme Gradient Boosting, XGBoost)实现的4种有监督学习射频干扰分类方法的效果进行了分析和比较。但该类基于有监督学习方法的关键问题是射频干扰分类准确度对特征选取非常敏感。为了减少对特征的依赖,文[1]将深度学习的方法应用于射频干扰消除,对模拟射频干扰信号取得了非常好的效果。但这种采用模拟数据对深度网络进行训练的方式,很难防止过拟合。
独立成分分析(Independent Component Analysis, ICA)起源于盲源信号分离(Blind Signal Separation, BSS)。盲源信号分离是信号处理中一个传统而又极具挑战的问题,指仅从若干观测的混合信号中恢复无法直接观测的各个原始信号的过程[14]。这里的 “盲”,既指源信号不可测,又指混合系统特性事先未知。所谓 “鸡尾酒会问题” 就是盲源信号分离的典型例子。独立成分分析是研究盲源信号分离的一种重要方法,基于信号高阶统计特性已成为阵列信号处理和数据分析的有力工具。显然,独立成分分析涉及的问题,在数学模型上本身是欠定的,但附加原始信号间统计独立及原始信号非高斯分布两个条件后,各原始信号可完美复原[15]。文中将射电望远镜观测到的脉冲星信号看作观测信号,包含其中的各射频干扰和脉冲星信号视为原始信号。各射频干扰信号和脉冲星信号间统计上相互独立且各信号符合非高斯分布,满足独立成分分析的假设条件。相比已有方法,首先,无需人为选择或构造射频干扰结构特征,不存在阈值选择的困惑;其次,不存在训练或学习过程,因此无需考虑构建训练样本的问题。使用该方法对云南天文台40 m射电望远镜接收到的脉冲星观测信号进行独立成分分析,分解出独立的射频干扰信号和脉冲星信号,进而实现射频干扰消除,取得良好的效果。
1 独立成分分析
独立成分分析是近年来发展起来的一种统计方法。该方法目的是将观测到的数据线性分解成统计独立的成分。为严格定义独立成分分析模型,使用统计隐变量模型表示n个同一时刻接收到的射电信号x1,…,xn(混合信号):
xi=ai1s1+ai2s2+…+ainsn,i=1,…,n,
(1)
其中,si表示包含在混合信号xi中的源信号(独立成分),即射频干扰信号或脉冲星信号。这里混合信号xi和独立成分si均可视为随机变量。为不失一般性,设xi和si为零均值(混合信号xi总是可以通过减去样本均值实现零均值化)。(1)式的矩阵形式为
x=As,
(2)
其中,x和s分别为由x1,…,xn和s1,…,sn组成的随机向量;矩阵A由(1)式系数元素aij组成,称为混合矩阵。(2)式即为独立成分分析模型,描述通过独立成分si得到混合信号xi的过程,目标是求解独立成分s,(2)式可调整为
s=Wx,
(3)
其中,矩阵W=A-1,称为解混矩阵。独立成分s为隐随机向量,意味着s不能被直接观测到,需要根据随机向量x估计混合矩阵A和独立成分s。显然,该问题在数学模型上欠定。但在附加两个假设条件后,问题变得可解:(1)独立成分si间相互统计独立;(2)独立成分si拥有非高斯分布。射频干扰产生于人类活动,而天文射电信号产生于宇宙天体,二者之间相互统计独立,且分布上也不会呈现高斯分布,因此射频干扰消除满足独立成分分析模型的假设条件。
1.1 独立成分分析估计
由概率论中心极限定理可知,多个独立随机变量的混合信号趋近于高斯分布。因此,在独立成分分析模型中,若干个独立成分si组成的混合信号xi比任一个独立成分si更接近高斯分布,于是可利用非高斯性作为分离信号之间独立性的度量。
求解基本独立成分分析问题的通用步骤有3步[15]:(1)数据(混合信号)的预处理,包括中心化、白化。(2)选择或定义非高斯性(独立性)度量,建立目标函数。该函数取极值时,估计出的独立成分之间非高斯性最大。目标函数代表一种分离准则,根据不同分离准则推导不同的独立成分分析估计算法。(3)用某种最优化方法最大(小)化目标函数,实现独立成分分析估计。依据非高斯性度量方法的不同,独立成分分析估计方法可分为基于峰度(Kurtosis)和负熵(Negentropy)两类。由于基于峰度的独立成分分析估计方法在实际应用中对边缘样本过于敏感,导致鲁棒性较差[16],因此本文采用基于负熵的方法对射电天文中的射频干扰进行估计。
负熵基于信息论中熵的概念。随机变量的熵可视为所表示信息的自由度,即越随机,熵越大。信息论的一个重要结果为:相同方差时,高斯随机变量熵最大[17],因此可用熵衡量随机变量的非高斯性。随机变量y的熵定义为
(4)
其中,ai为y的可能取值。由(4)式可知,熵为负值。为方便描述随机变量的非高斯性,负熵定义为
J(y)=H(ygauss)-H(y),
(5)
其中,ygauss为与y具有相同方差的高斯随机变量。(5)式表明,对于高斯随机变量负熵为0,而其他情况则非负。从统计理论出发,负熵是对非高斯性估计的最优方法[18]。但使用(5)式计算负熵时,涉及到估计信号的概率密度函数,这在实际应用中往往非常困难,因此通常采用更简单的方式近似计算负熵。
1.2 负熵的近似
基于最大熵原理,文[19]提出了对负熵的近似方法:
(6)
其中,ki为正常数;v为零均值和单位方差的高斯随机变量;Gi为非二次函数。需要注意的是(6)式为非负,且当随机变量y呈现高斯分布时,其值为0。
当仅使用一个非二次函数时,对任意非二次函数G,(6)式近似为
J(y)∝{E[G(y)]-E[G(v)]}2.
(7)
关键之处在于函数G的选择。一般情况下,选择非快速增长函数G,通过(6)式可得到更鲁棒的负熵估计。例如,下列G函数被证明在负熵估计中非常有效[19]:
(8)
其中,a1为介于1与2之间的常数,通常取a1=1。实际应用中可使用快速独立成分分析(FastICA)算法[20]寻找(7)式表示的非高斯性最大值。
2 基于独立成分分析的射频干扰消除的实现
上面介绍了独立成分分析模型、负熵近似以及快速迭代求解对比函数的方法。为使算法更为高效,将独立成分分析运用到射频干扰消除前,需考虑数据初始化问题。此外,如何从分解得到的独立成分中选出脉冲星信号也是实现的关键。
2.1 射电数据预处理
实现中,数据预处理包括中心化和白化。所谓中心化,是将观测到的射电信号处理为零均值。可通过观测向量x减去均值向量m=E{x}实现。此时,对(2)式两边取期望可知,独立成分s也为零均值。中心化的目的在于简化独立成分分析估计。使用中心化后的射电观测数据估计出混合矩阵A后,可将s的均值向量A-1m加到零均值独立成分s上,从而完成独立成分估计。
白化可减少独立成分分析中的参数。所谓白化,是将观测到的射电信号x转换为非相关且具有单
E{xxT}=EDET,
(9)
其中,E为E{xxT}特征向量的正交矩阵;D为其特征值构成的对角矩阵,D=diag(d1, …,dn)。注意,(9)式的值可通过不同时刻射电观测信号x(1),…,x(t)得到,因此,白化可记为
(10)

(11)
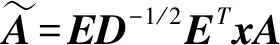
(12)
为便于表述,下面所描述的射电观测信号x为中心化和白化后的数据,而混合矩阵统一表述为A。
2.2 主信号分离
文[21]证明了独立成分分析的含混性——独立成分分析不能确定独立成分的顺序,即通过独立成分分析模型,可由射电观测信号x估计出混合矩阵A(或解混矩阵W),进而得到源信号s,但无法确定s的组成成分s1,…,sn中,哪些是脉冲星信号,哪些是射频干扰。
观察图1脉冲星观测数据可发现:(1)数据列在相位上对齐,因此脉冲星观测信号(图像)x的每一行可视为一个相变信号:x1(t),…,xn(t),由此估计的源信号向量s也由相变信号s1(t),…,sm(t)组成,为保证A是满秩矩阵,要求n≥m;(2)相对于射频干扰信号,脉冲星信号呈现强宽带特性,即对于脉冲星信号,数据行与行之间有更强的相关性。此外,由(2)式可知,矩阵A第i行元素实质上是将源信号s1(t),…,sm(t)混合成第i个频率通道观测信号xi(t)的权重;第j列元素对应于将第j个源信号sj(t)混合到各频率通道观测信号x1(t),…,xn(t)的权重。由混合矩阵A各元素含义及上述发现(2)可知,若sj(t)对应脉冲星信号,则矩阵A第j列将呈现均匀分布的特点,可用方差或标准差衡量随机变量均匀分布的程度。此外,实际中射频干扰源数目不可预知,且一般有n大于射频干扰源数目,由此会造成矩阵A某些列标准差很小且中值也很小,此时这些列对应射频干扰信号。根据以上分析,可用标准差向量std与中值向量med点除得到判别向量d,即某一列中值越大,标准差越小,则对应该判别向量元素值越大:
d=med·/std,
(13)
其中,标准差向量和中值向量分别由矩阵A各列标准差std1, …,stdm和中值med1, …,medm组成,即
(14)
其中,μj和Nj分别表示矩阵A第j列均值和元素个数;median()表示中值函数。若第jp个源信号sjp(t)对应脉冲星信号,则其余sj(t)(j≠jp)对应射频干扰信号。由上述分析可知,应选择判别向量元素最大值所在列对应的源信号为脉冲星信号。即jp为
(15)
其中,d1, …,dm组成判别向量d。需注意,此时sjp(t)包含了各频率通道的脉冲星信号信息,并非图1展现的形式。由混合矩阵A各元素含义可知,通过以下变换可得到以图1形式呈现的去除射频干扰后的脉冲星信号:
xp=Aps,
(16)
其中,矩阵Ap通过保留混合矩阵A第jp列元素,并置其余列元素为0得到。
2.3 次信号分离
由于FastICA是对负熵求近似解,少量脉冲星信号包含在其他独立成分sj(t)(j≠jp)中。需要对矩阵Ap进一步修正,使得恢复的信号xp尽可能完整地包含脉冲星信号,同时尽量少包含射频干扰。注意到残留脉冲星信号不论在频率上还是脉冲相位上分布相对射频干扰更均匀。通过实验发现,可将k倍矩阵A除去第jp列后的标准差作为阈值,并把矩阵A中满足
|aij| (17) 的元素加入Ap中,以修正Ap。修正后的Ap通过(16)式可较完整地恢复脉冲星信号。(17)式中std(Ap~)表示矩阵A除去第jp列元素后的标准差。系数k选取过小,少量脉冲星信号会被当作射频干扰消除,过大则射频干扰消除不彻底。需要指出的是,本文算法对k值并不敏感,取0.5 ≤k≤ 2.5可获得信噪比大于50的脉冲星积分轮廓,满足改善脉冲星观测的需求。在遵循消除射频干扰且尽量保持脉冲星信号这一原则下,选取k=1。 实验数据来自云南天文台40 m射电望远镜S波段脉冲星日常观测结果,观测终端为从澳大利亚联邦科学与工业研究组织引进的第四代脉冲星数字滤波器组(Pulsar Digital FilterBank 4, PDFB4)。PDFB4对观测数据处理过程包括:非相干消色散和周期轮廓折叠。数据采样实现对脉冲星信号数据采集(采样率为64 μs)。观测中心频率2 256 MHz,脉冲星的观测方式为非相干消色散,观测配置为512 MHz-512Bin-512Chan,30 s的子积分,数据存储为PSRFITS格式。由于40 m射电望远镜距离昆明市区较近,存在较强的射频干扰,如2 G,3 G,4 G手机信号和WIFI频段。为避免引起观测设备系统饱和,观测时需利用滤波器在射频波段直接将上述信号剔除,剔除上述干扰后,S波段仅留下60 MHz至140 MHz相对干净的观测带宽。实际观测频段为2 170~2 310 MHz,在该带宽内仍存在各种类型的未引起系统饱和的干扰。 为验证本文方法的效果和可行性,利用该方法对J0332 + 5434脉冲星观测数据进行处理。选取该脉冲星在2017年S波段日常观测中比较有代表性的观测数据。图2(a)非常清晰地显示,观测干扰频点分别为2 231~2 241 MHz,2 252~2 258 MHz,2 267~2 273 MHz,2 300~2 308 MHz。其中第2、3个干扰频点呈现干扰信号强、持续时间长的特点,而第1个干扰频点非常弱,通过多个子积分后在图3(a)中相对明显,第4个干扰频点在相位上显现不确定性,实验结果如图2(b)。从图中可看出射频干扰基本消除,仅保留PSR J0332 + 5434脉冲星信号。图2(c)则显示了图2(a)与(c)的差值信号,即射频干扰信号。 图2 J0332 + 5434射频干扰消除效果。(a) 观测数据;(b) 射频干扰消除结果;(c) 差值信号 通过实验,还可以对与独立成分分析在原理上有相似之处的主成分分析方法(Principal Component Analysis, PCA)进行对比分析和讨论。独立成分分析和主成分分析同属因子分析,都是通过线性组合后使得某种特征最大化。主成分分析方法寻求方差最大化,而独立成分分析寻求非高斯性最大化;主成分分析方法找出信号中不相关部分,对应二阶统计量分析,独立成分分析找出构成信号的相互独立部分,对应高阶统计量分析。但主成分分析和独立成分分析用途不同。主成分分析方法是目前数据降维的常用方法,如果只在意数据的能量或方差,假设干扰信号比较微弱,可用主成分分析方法分离出主要信号。但在射频干扰消除中,很多情况下强弱干扰混合在一起,例如,图2(a)显示的脉冲星观测信号中,位于2 252~2 258 MHz,2 267~2 273 MHz频点的干扰明显强于脉冲星信号,而2 231~2 241 MHz频点的干扰信号又比脉冲星信号弱很多,2 300~2 308 MHz频点的干扰信号在强度上与脉冲星信号接近。使用主成分分析方法,如果以信号强度度量,很难确定哪些主分量对应射频干扰,哪些对应射电信号。而在某种意义上,独立成分分析更智能,它不在意信号的能量或方差,只看独立性。给定待分解的混合信号经任意线性变换不会影响独立成分分析的输出结果,但会严重影响主成分分析的结果。当然如果能找到除能量之外的其他特征,并且在此特征维度下使射电信号能成为主分量,而射频干扰成为次分量,则可以运用主成分分析方法分解射电信号和射频干扰。 在现实应用中,对脉冲星连续观测信号取均值是一种有效且常用的射频干扰消除手段。图3(a)显示了对PSR J0332 + 5434脉冲星连续96个子积分观测信号求取均值的结果。图中可明显看到,在脉冲星信号增强的同时,射频干扰信号也被强化。图3(b)为采用本文方法对96个子积分观测信号分别消除射频干扰,然后求取均值的结果,图中可以看出,在较好保留脉冲星信号的同时,射频干扰信号基本消除。图3(c)为图3(a)与(b)的差值信号,即96个子积分观测信号求取均值后的射频干扰信号。图3(a)~(c)展示了本文方法对脉冲星观测信号中射频干扰消除的明显效果。然而仔细观察,图3(c)中出现了少量脉冲星信号残余。这主要由于FastICA是对负熵求近似解,从而导致2 231~2 241 MHz弱射频干扰信号与残留的少量脉冲星信号对应的独立分量难以区分。但相对于目前普遍采用的均值方法,本文方法明显改善了脉冲星观测信号。这一效果也能从图4的脉冲星轮廓中得到。 图3 J0332 + 5434积分均值信号射频干扰消除效果。(a) 观测信号积分均值;(b) 射频干扰消除结果;(c) 差值信号 Fig.3 RFI mitigation for J0332 + 5434 after mean of accumulation. (a) observed signal after mean of accumulation; (b) RFI mitigation result; (c) difference signal 为更直观反映本文方法的有效性,图4显示了对图3(a),(b)沿频率域积分后的脉冲星轮廓图。其中,图4(a)为均值法消除射频干扰后的脉冲星信号积分轮廓图;图4(b)为(17)式中k=1时,采用本文方法消除射频干扰后的脉冲星信号积分轮廓图。两幅轮廓图中均能清晰看到PSR J0332 + 5434脉冲星的三峰结构,但对比均值法消除结果可以看出,本文方法有效消除了观测信号中的射频干扰信号,且脉冲星信号得到较完整保留。此外,通过脉冲星轮廓信噪比(Signal Noise Ratio, SNR)定义[22]: (18) 图4 不同方法消除射频干扰后J0332 + 5434脉冲星轮廓图对比。(a) 均值法;(b) 本文方法 Fig.4 Comparison of pulse profiles of PSR J0332 + 5434 after different method of RFI mitigation.(a) mean of accumulation (b) approach proposed by this paper 图5显示了(17)式中k取0~3时,采用本文方法对PSR J0332 + 5434脉冲星连续96个子积分观测信号进行射频干扰消除并求取均值后积分轮廓图信噪比的变化情况。由图可以看出,在k=0.69时,信噪比达到峰值60.37,之后开始衰减。分析原因,k较小时,在射频干扰消除结果中由(17)式引入的残留脉冲星信号对信噪比提升产生的贡献大于由此引入的射频干扰对信噪比的影响,从而信噪比上升;但随着k的增加,过多引入弱射频干扰的负面影响增大,导致信噪比下降。值得注意的是,取0.5 ≤k≤ 2.5可获得信噪比大于50的脉冲星积分轮廓。通过(17)式在射频干扰消除结果中尽量包含完整的脉冲星信号是一个相互平衡的过程,因此实现时,在遵循消除射频干扰且尽量保持脉冲星信号这一原则下,并未选取信噪比达到峰值时的k值,而是选取k=1。相对目前常用的对脉冲星连续观测信号取均值以提高信噪比的方法,本文方法对信噪比提升效果明显。此效果在图2~图4实验结果中也有所反映。 图5k值对射频干扰消除信噪比影响 射频干扰广泛存在于射电天文观测中,而脉冲星观测信号可视为射频干扰信号与脉冲星信号的混合信号。基于各射频干扰信号和脉冲星信号间统计上相互独立且各信号符合非高斯分布的特性,本文提出基于独立成分分析的射频干扰消除方法。相比已有方法,首先,无需人为选择或构造射频干扰结构特征,不存在阈值选择的困惑;其次,不存在训练或学习过程,因此无需考虑构建训练样本的问题。使用该方法对云南天文台40 m射电望远镜接收到的脉冲星观测信号进行独立成分分析,分解出独立的射频干扰信号和脉冲星信号,进而实现射频干扰消除。本文方法在干扰信号消除、射电信号保留及信噪比方面均取得较好的效果,为进一步提高脉冲星观测数据利用率奠定良好的基础。此外,本文方法不仅适用于脉冲星射电信号处理,对其他射电天文信号处理也具有借鉴意义。但是,由于FastICA对负熵求近似解,使得弱射频干扰信号与残留的少量脉冲星信号对应的独立分量区分度较小,导致出现残差图像中存在少量脉冲星信号的问题。 致谢:感谢国家天文台-阿里云天文大数据联合研究中心对本文工作提供的支持。3 实 验
3.1 实验数据
3.2 实验结果
Fig.2 RFI mitigation for J0332 + 5434. (a) observed signal; (b) result of RFI mitigation using ICA; (c) difference signal
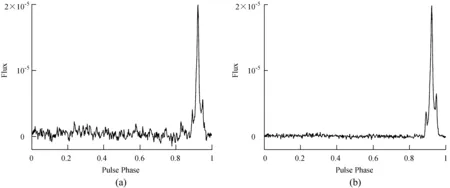

Fig.5 Impact ofkon signal noise ratio in RFI mitigation4 结 论
