Analysis of the mass of behind-armor debris generated by RHA subjected to normal penetration of variable cross-section EFP

Boyng Xing , Dongjing Zhng , Zhenyn Guo , Yunhui Hou , Rui Guo ,*,Rongzhong Liu , Ling Chen , Ho Zhou , Yongling Yng , Jinhu Luo

a School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China

b Xi'an Modern Control Technology Research Institute, Xi'an 710065, Shanxi, China

c School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China

Keywords:Explosively formed projectile Behind-armor debris Variable cross-section characteristic Shape of plug Axial length of mushroom Theoretical model

A B S T R A C T Analyzing the mass of behind-armor debris (BAD) generated by Rolled Homogeneous Armor (RHA)subjected to normal penetration of variable cross-section Explosively Formed Projectile (EFP) is the purpose of this paper.So theoretical analysis,numerical simulation and experimental data are combined to analyze the influence of variable cross-section characteristic on the time history of crater radius.Moreover the relationships between time history of crater radius (as well as mass of BAD) and the thickness of RHA(from 30 mm to 70 mm)and the impact velocity of EFP(1650 m/s to 1860 m/s)are also investigated. The results indicate that: 1) being compared to the variable cross-section characteristic is ignored, the theoretical time history of crater radius is in better agreement with the simulation results when the variable cross-section characteristic is considered; 2) being compared to the other three conditions of plug,the theoretical mass of BAD is in the best agreement with the simulation results when the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45° and the axial length of mushroom is considered.

1. Introduction

It is significant to predict the mass, number and velocity distribution of BAD generated by RHA subjected to penetration of EFP by the thickness of target and the impact velocity of EFP, and obtaining the mass of BAD generated by RHA and EFP accurately is the basement of the prediction [1-5,30].

The A-T model established by Alekseevskii[10]and Tate[11-14]has achieved good results in penetration problem. Many scholars[15-22] have developed A-T model, but the main part of the penetrator is slender and equal cross section cylindrical rod, and they do not consider the small length-diameter ratio and the variable cross section. Alekseevskii [10], Tate [11-14], Rosenberg [15], and Grace [16,17] neglected the influence of the axial length of mushroom in penetration process when studying the long rod penetration.Li[2]and Zhang[3]neglected the influence of the axial length of mushroom in penetration process when studying the normal penetration of EFP into steel target.Rosenberg[27]pointed out that shapes of plug block are different when penetrating the finite thickness target with different penetrator nose shapes. Zhang [3]considered that the plug had two shapes, namely cylinder and frustum of a cone and the angle between generatrix and bottom is 45°when studying the normal penetration of EFP into steel target,and the latter was chosen as combining with the specific research object.Held[23,24]gave the radial crater growth model neglecting the strength of jet.Li[2]neglected the strength of EFP and applied the Held model [23,24] directly when analyzing the behind armor effect of EFP, so it is inconsistent with the actual situation. The theoretical studies on the behind armor effect are all based on the penetrator whose main part is slender and equal cross section cylindrical rod [25,26]. The studies about behind armor effect of EFP mostly focus on numerical simulations and experiments [4-7],while the variable cross-section characteristic of EFP has not been considered in the theoretical study about BAD generated by target subjected to penetration of EFP.The penetration theory derived by penetrator whose main part is slender and equal cross section cylindrical rod cannot be directly applied to EFP, since EFP has the characteristic of variable cross-section. And the influence of the axial length of mushroom in penetration process cannot be ignored,since the EFP has a small length-diameter ratio.The shape of plug produced by the finite thickness target is uncertain,since the shape of EFP nose is irregular.The strength of EFP cannot be ignored like a jet,since the stand-off distance of EFP is so long(up to 1000 times the diameter of the charge)and the velocity of EFP is much slower than jet.And theoretical mass of BAD generated by finite thickness RHA subjected to normal penetration of EFP based on the above existing theories may lead to a large error.

So based on our previous work[30],combined with theoretical analysis, numerical simulation and experimental data, variable cross-section characteristic and strength of EFP are taken into consideration, then the relationship between the mass of BAD generated by RHA and EFP and the thickness of RHA and the impact velocity of EFP are obtained when the axial length of mushroom and the shape of plug are different.Finally,whether the axial length of mushroom need to consider and which shape of plug is suitable are decided.

2. Theoretical model

The laser high-speed photography and the equivalent numerical simulation model of the typical EFP were both introduced in details in Ref.[30].It can be found from Refs.[9,30]that EFPs have variable cross-section characteristic, and their cross section radius vary at different axial positions. Therefore, variable cross-section is a key characteristic of EFP, and the effect of variable cross-section characteristic on crater radius by penetration mechanism is needed to analyze.

First of all, two assumptions just as in Ref. [30] are need to simplify the penetration process:(1)The crater phases is short and the energy of EFP is consumed little;thus,the influence of crater on penetration can be ignored; (2) the initial stagnation radial pressure is equal to axial pressure, and radial pressure changes as the crater radius.

The process diagram for the typical EFP penetrating RHA normally is drawn in Fig.1.

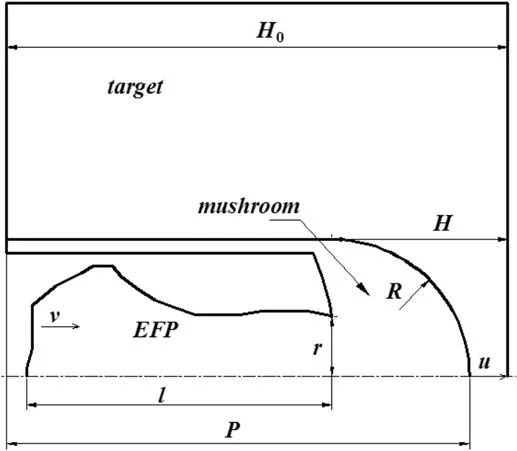
Fig.1. The process diagram for the typical EFP penetrating RHA normally.

The axial force of the EFP on the RHA can be obtained from Ref. [30] that

and the crater velocity is

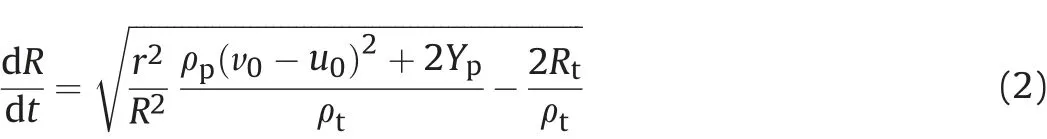
and the penetration depth of EFP when the plug is formed is

where R is the radius of crater (mushroom), r is the cross section radius of EFP, u is the penetration velocity, v is the velocity of undeformed part of EFP,t is the penetration time and the penetration starts at t=0. And ρtand Rtare the density and strength factor of RHA respectively, ρpand Ypare the density and strength factor of EFP respectively.And u0is the penetration velocity at t=0,v0is the impact velocity of EFP. And the subscript c represents the parameters when the plug is just formed, for example, tcis the forming time of plug.

As the nose shape of the EFP is irregular, it is impossible to determine the shape of plug.

In Ref. [30], an assumption was made that the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°,furthermore the axial length of mushroom is considered.Now this assumption is ignored and the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°or cylinder is assumed,what's more the axial length of mushroom could be considered or ignored.

If the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°, then parameters when the plug is formed are shown in Fig. 2, and in which the meshes are the internal fragments of the plug.

Fig. 2. The shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°.

The axial shear force of the plug is equal to the axial force of EFP on RHA, as equation (4) shows.

where τmaxis the maximum shear strength of RHA and the calculation method was introduced in details in Ref. [30].

If the axial length of mushroom is ignored,then,

where H0is the thickness of RHA. And the mass of BAD generated by RHA satisfies the following relation,

The residual mass of EFP is the mass of undeformed part of EFP,so mass of BAD generated by EFP satisfies the following relation,

If the axial length of mushroom is considered, then,

Then the mass of BAD generated by the RHA satisfies the following relation,

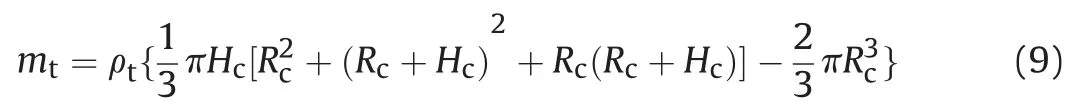
The residual mass of EFP is the sum mass of undeformed part of EFP and mushroom, so the mass of BAD generated by EFP satisfies the following relation,

If the shape of plug is cylinder, Fig. 3 shows parameters when the plug is formed.

And the axial shear force of the plug is equal to the axial force of EFP on RHA, as

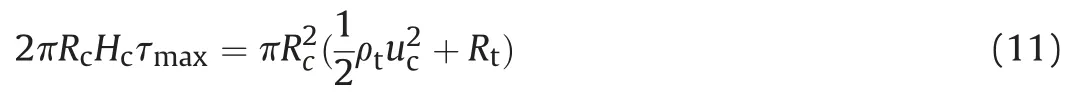
If the axial length of mushroom is ignored, the mass of BAD generated by EFP satisfies equation (7), and the mass of BAD generated by RHA satisfies the following relation,

If the axial length of mushroom is considered,the mass of BAD generated by EFP satisfies equation (10), and the mass of BAD generated by RHA satisfies the following relation,

Since the crater radius is not considered after the formation of the plug, the time range is 0 ≤t ≤tc.

3. Numerical simulation model verification

The main parameters of the numerical simulation and the main parameters of experimental setting about the formation of EFP had already been introduced in details in our previous work [8,9] and the credibility of numerical simulation method had already been proved in Refs. [8,9].

Fig. 3. The shape of plug is cylinder.

Dalzell [4] used AUTODYN-3D™to simulate the formation of BAD clouds subjected to penetration of EFP, and pointed out that the SPH algorithm had more advantageous than the Lagrange and Euler algorithms in the study of BAD.Yarin[25]found that the mass loss range of target is nearly 30% in the experimental study of tungsten alloy long rod penetrating RHA. And it was often found that the BAD generated by RHA and EFP would be bonded together[30].

Therefore, the SPH algorithm in AUTODYN-3D™was used to simulate the experiment in Ref. [5] to verify the credibility of the numerical simulation method by results that could be measured accurately. Then the verified numerical simulation method was used to simulate BAD generated by RHA subjected to normal penetration of the typical EFP,in order that the results obtained by theoretical model whose error range was large in experiments could be verified [30].

The types of material, equations of state and constitutive relations in the numerical simulation model were all the same as that in Ref.[5],the main parameters of the simulation had already been introduced in details in Ref. [5], while the main parameters of the experimental setting had already been introduced in details in Ref. [30]. And the credibility of numerical simulation method had also been proved in Ref. [30].

4. The time history of the crater radius

4.1. The effect of variable cross-section characteristic

The parameters in theoretical model are all taken from Refs.[14,20,28,29],the calculation method of Ypand Rtcan be found in Ref. [14]. The main parameters are: τ0=0.907, n=0.25,p' = 8.0*107s-1, q=7.33, α = 6.8*10-4, β=0.9, Cv=452 J/kgK,Et=210 GPa,λ=0.7,ρp=8.93 g cm-3,ρt=7.85 g cm-3.

In order to obtain the effect of variable cross-section characteristic,the theoretical tcis needed to obtain and the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom head needs to be considered should be assumed in Section 4 as it is proved right in Ref. [30] and it will be proved right in the end of this paper.

An example that the typical EFP penetrating a 70 mm-thick RHA normally at the impact velocity of 1650 m/s can be calculated by theoretical method and numerical simulation method.

The theoretical tcis around 100μs no matter the variable crosssection characteristic is considered or ignored and the time history of the crater radius is shown in Fig. 5. Var. represents the results that the variable cross-section characteristic of EFP is considered.Con. represents the results that the variable cross-section characteristic of EFP is ignored and Sim. represents the numerical simulation results.

The laser high-speed photography and the equivalent numerical simulation model of the typical EFP were both introduced in details in Ref. [30]. The numerical simulation model of BAD generated by RHA subjected to normal penetration of the typical EFP is shown in Fig. 4, and the blue part is the typical EFP, the green part is target,the red part is a fixed constraint applied to the boundary of target.And the particle size the SPH algorithm in AUTODYN-3D™is 0.5 mm.In order to reduce the influence of the boundary effect,the length and width of the target are both 1000 mm which are more than 17 times of the maximum diameter of the typical EFP.And the numerical simulation method has been introduced in details in Ref. [30].

It can be found from Fig. 5 that being compared to the variable cross-section characteristic is considered, the theoretical time history of crater radius is in the better agreement with the simulation result when the variable cross-section characteristic is considered.

When the variable cross-section characteristic is considered, it can be found from Ref.[30]that the radius of the typical EFP at the EFP-mushroom interface increases quickly at first, then decreases slowly, and then increases quickly, finally decreases slowly to the end of the penetration. It can be found from equation (2) that R increases quickly at first(stage Var.I),then increases slowly(stage Var.II,R ≈RVar.II(constant)),and then increases quickly(stage Var.III),finally increases slowly to the end of the penetration(stage Var.IV).The radius of the typical EFP at the EFP-mushroom interface is a constant when the variable cross-section characteristic is ignored,so the crater velocity is a positive value, and the value of r/R gradually decreases during the penetration.And R increases quickly at first (stage Con. I), then keeps increasing slowly (stage Con. II,R ≈RCon.II(constant)), and RVar.II≈RCon.IIcan be obtained by theoretical calculation.

To sum up, the variable cross-section characteristic must be considered to calculate the time history of crater radius when EFP normally penetrating RHA.

Fig. 4. Simulation model of the typical EFP.

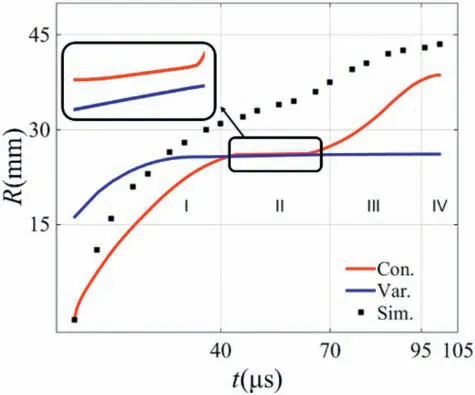
Fig. 5. The time history of the crater radius.

4.2. The effect of the thickness of RHA

It can be found from the theoretical analysis that the thickness of RHA affects crater time as well as crater radius.The time history of the crater radius in Fig. 6 can be obtained by the theoretical calculation,while the typical EFP normally penetrates RHA with the thickness of 30 mm, 40 mm, 50 mm, 60 mm and 70 mm at the impact velocity of 1650 m/s.

As the impact velocity of EFP is a constant,the penetration time increases with the increase of the thickness of RHA, so the crater time is constantly increasing.The theoretical analysis shows that Rcgradually transits from the stage II to the stage III,and finally enters the stage IV when the thickness of RHA is between 30 mm and 70 mm,so it can be found from Fig.6 that the final crater radius is constantly increasing.Moreover,the crater radius is the same at the same time under different thickness of RHA since the shape of EFP is fixed.

4.3. The effect of the impact velocity of EFP

It can be found from the theoretical analysis that the thickness of RHA affects the crater time as well as the crater radius.The time history of the crater radius in Fig. 7 can be obtained by the theoretical calculation, while the typical EFP normally penetrates RHA with the thickness of 40 mm at the impact velocity of 1650 m/s,1680 m/s,1740 m/s,1800 m/s and 1860 m/s.

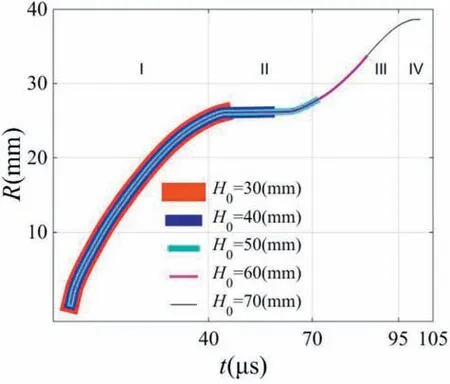
Fig.6. The time history of the crater radius under different thickness of RHA condition.

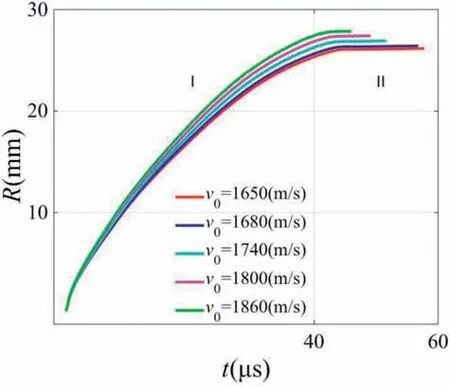
Fig. 7. The time history of the crater radius under different impact velocity of EFP condition.

It can be known from equation (2) that the crater velocity is increasing with the increase of the impact velocity of EFP, and the thickness of RHA is a constant,so the crater radius of larger impact velocity of EFP is larger when the crater time is same.It can also be found from Fig.6 that Rcin Fig.7 has not experienced the stages III and IV since the thickness of the RHA is not large enough. So although the crater time of larger impact velocity of EFP is shorter,the final crater radius is constantly increasing with the increase of the impact velocity of EFP.

5. The mass of BAD

5.1. The effect of the thickness of RHA

It can be found from the theoretical analysis that the parameters of the shape of plug directly determine the mass of BAD generated by RHA, and indirectly affect the mass of BAD generated by EFP.However,the parameters of the shape of plug are closely related to the thickness of RHA, so the thickness of RHA is one of the main factors that affects the mass of BAD.

The typical EFP normally penetrates RHA whose thickness are 30 mm, 40 mm, 50 mm, 60 mm and 70 mm at the impact velocity of 1650 m/s.The simulation results of the mass of BAD generated by RHA and EFP as well as the theoretical results under 4 conditions of plug as the variable cross-section characteristic is considered are shown in Fig. 8.

And Sim. is the simulation result, mtis the mass of BAD generated by RHA, mpis the mass of BAD generated by EFP. Four conditions of plug are:1)the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is ignored (FCN); 2) the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is considered(FCT);3)the shape of plug is cylinder and the axial length of mushroom is ignored (CYN); 4)the shape of plug is cylinder and the axial length of mushroom is considered (CYT).

It can be found from Fig. 8 that being compared to other three conditions of plug, the theoretical mass of BAD generated by RHA and EFP are in the best agreement with the simulation results when the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is considered.

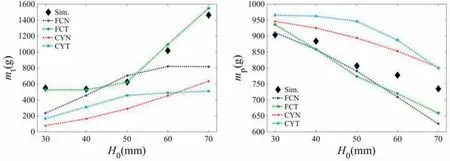
Fig. 8. The mass of BAD generated by RHA and EFP under different thickness of RHA condition.

It is inconsistent with the trend of the simulation results that the theoretical mtincreases quickly at first,then increases or decreases slowly with the increase of the thickness of RHA when the conditions of plug are CYT and FCN. The theoretical mtkeeps increasing quickly with the increase of the thickness of RHA when the condition of plug is CYN, but the deviation between it and the simulation results is large.

Table 1The deviations between theoretical mass and simulation results.

Table 2The average deviations.

The theoretical mtis in the best agreement with the simulation results when the condition of plug is FCT.It can be found from Fig.6 that Rcgradually transits from the stage II to the stage III,and finally enters the stage IV with the increase of the thickness of RHA.Since Rcincreases rapidly in stage III,it can be found from the theoretical analysis in Ref. [30] that Rc is the main factor that effects mt. So it can be known from equation(9)that mt keeps nearly a constant at first, then increases rapidly and finally increases slowly with the increase of the thickness of RHA. Since the erosion length of EFP increases with the increase of the thickness of RHA, mp decreases with the increase of the thickness of RHA.

In order to make a quantitative comparison, the deviations between the theoretical mass of BAD generated by RHA and EFP under 4 conditions of plug and simulation results are shown in Table 1.For example,when the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is considered, the deviation between the theoretical mass of BAD generated by RHA and simulation result can be obtained as: FCNt=|(mtFCN-mtSim)/mtSim|*100%. The calculation method of the other 7 deviations is similar to this.

The average deviations between the theoretical results under the same condition of plug and simulation results are shown in Table 2. For example, when the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is considered,the average deviation between the theoretical results and simulation results can be obtained as:FCNt=(FCNt|H0=30+FCNp|H0=30+FCNt|H0=40+FCNp|H0=40+FCNt|H0=50+FCNp|H0=50+FCNt|H0=60+FCNp|H0=60+FCNt|H0=70+FCNp|H0=70)/10. The calculation method of the other 3 deviations is similar to this.

It can be obviously found from Table 2 that the average deviation between the theoretical results and simulation results is the minimum when the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is considered.It indicates that being compared to other three conditions of plug,mass of BAD generated by RHA and EFP is in the best agreement with the simulation results under this condition of plug.

5.2. The effect of the impact velocity of EFP

It can be found from the theoretical analysis that the impact velocity of EFP has a significant influence on the initial penetration velocity, erosion rate and radial pressure, and they are closely related to the critical conditions of the formation of the plug,so the impact velocity of EFP is one of the main factors that affects the mass of BAD.

The typical EFP normally penetrates RHA whose thickness are 40 mm at the impact velocity of 1650 m/s, 1680 m/s, 1740 m/s,1800 m/s and 1860 m/s. The simulation results of the mass of BAD generated by RHA and EFP as well as the theoretical results under 4 conditions of plug as the variable cross-section characteristic is considered are shown in Fig. 9.

It can be found from Fig. 9 that being compared to other three conditions of plug, the theoretical mass of BAD generated by RHA and EFP are in the best agreement with the simulation results when the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is considered.

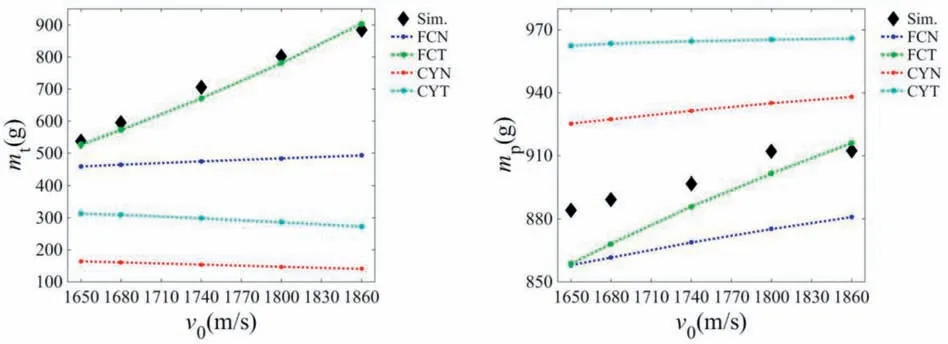
Fig. 9. The mass of BAD generated by RHA and EFP under different impact velocity of EFP condition.

Table 3The deviations between theoretical mass and simulation results.

Table 4The average deviations.

It is inconsistent with the trend of the simulation results that the theoretical mtdecreases constantly with the increase of the impact velocity of EFP when the conditions of plug are CYN and CYT. The theoretical mtincreases so slowly with the increase of the impact velocity of EFP when the condition of plug is FCN,and the deviation between it and the simulation results is large. The deviation between the theoretical mpand the simulation results is large when the condition of plug is FCN, CYN and CYT.

The theoretical mtand mpare in the best agreement with the simulation results when the condition of plug is FCT. Since the thickness of RHA is 40 mm and does not change any more, the penetration time is the longest when the impact velocity of EFP is 1650 m/s. But it can be found from Fig. 7 that Rc is in stage II,namely Rc increases slowly and it can be known from Ref.[30]that the main factor that effects Rc is the impact velocity of EFP while the penetration time is the minor factor. So Rc and uc keeps increasing with the increase of the impact velocity of EFP and it can be known from equation (9) that mt keeps increasing. Since the penetration time decreases with the increase of the impact velocity of EFP, the erosion length of EFP keeps decreasing and mp keeps increasing with the increase of the impact velocity of EFP.

In order to make a quantitative comparison, the deviations between the theoretical mass of BAD generated by RHA and EFP under 4 conditions of plug and simulation results are shown in Table 3,the calculation method is similar to that in Section 5.1.

The average deviations between the theoretical results under the same condition of plug and simulation results are shown in Table 4, the calculation method is similar to Section 5.1.

It can be obviously found from Table 4 that the average deviation between the theoretical results and simulation results is the minimum when the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is considered.It indicates that being compared to other three conditions of plug,mass of BAD generated by RHA and EFP is in the best agreement with the simulation results under this condition of plug.

6. Conclusions

This paper draws the following conclusions:

(1) Being compared to the variable cross-section characteristic is ignored, the theoretical results of the time history of crater radius are in the better agreement with the simulation results when the variable cross-section characteristic is considered.

(2) As the impact velocity of EFP is 1650 m/s,with the thickness of RHA from 30 mm to 70 mm,the crater radius is the same at the same crater time, the final crater radius is constantly increasing; as the thickness of RHA is 40 mm, with the increase of the impact velocity of EFP from 1650 m/s to 1860 m/s, the crater radius of larger impact velocity of EFP is larger when the crater time is same, the final crater radius is constantly increasing.

(3) Being compared to other three conditions of plug, it can be found that the theoretical mass of BAD generated by RHA or EFP are in the best agreement with the simulation results when the shape of plug is frustum of a cone and the angle between generatrix and bottom is 45°and the axial length of mushroom is considered.

(4) As the impact velocity of EFP is 1650 m/s,with the thickness of the RHA from 30 mm to 70 mm, the mass of BAD generated by RHA keeps basically the same firstly, and then increases quickly while the mass of BAD generated by EFP constantly decreases;as the thickness of RHA is 40 mm,with the increase of the impact velocity of EFP from 1650 m/s to 1860 m/s, the mass of BAD generated by RHA and EFP constantly increases.

Funding statement

This work was financially supported by the National Natural Science Foundation of China (Grant No.11372136).