Real-time calculation of fragment velocity for cylindrical warheads

Dvid Felix, In Colwill , Elis Stipidis ,b,c

a Institution of Engineering and Technology, Stevenage, England

b Member of British Computer Society, London

c Institute of Electrical and Electronics Engineers, London

Keywords:Initial fragment velocity Real-time simulation Cylindrical explosion

A B S T R A C T To simulate explosion fragments,it is necessary to predict many variables such as fragment velocity,size distribution and projection angle. For active protection systems these predictions need to be made very quickly,before the weapon hits the target.Fast predictions also need to be made in real time simulations when the impact of many different computer models need to be assessed.The research presented in this paper focuses on creating a fast and accurate estimate of one of these variables - the initial fragment velocity.The Gurney equation was the first equation to calculate initial fragment velocity. This equation,sometimes with modifications,is still used today where finite element analysis or complex mathematical approaches are considered too computationally expensive. This paper enhances and improves Breech’s two-dimensional Gurney equation using available empirical data and the principals of conservation of momentum and energy. The results are computationally quick, providing improved accuracy for estimating initial fragment velocity. This will allow the developed model to be available for real-time simulation and fast computation, with improved accuracy when compared to existing approaches.

1. Introduction

Today a modern active protection system such as the Defence Aid System (DAS) relies on computer processors with a quick reaction time.An active protection system identifies a threat and can quickly assemble a response before the threat strikes; thereby reducing the potential damage. The computer incorporated into such a scheme must be able to assess multiple simultaneous threats, with very short warning periods, within fractions of a second.

Fast computer processors are also required to gauge the effect of various threats on a vehicle, under design, to allow a designer to determine the optimum armour and/or vehicle architecture required to increase a vehicle's survivability [1]. Faster computer models allow more threats to be assessed early in the design cycle which allows designers to consider a larger range of design options[2].

One of the main threats to a military asset is an explosion which is a complex physical event involving many variables.Many of these variables were first successfully analysed during World War II by people such as Gurney [3], Taylor [4] and Mott [5]. The resulting equations were simple, reasonably accurate and suitable for manual calculation as they were derived before the widespread availability of computer systems.

Since World War II, with the progress of computers, more complicated models have been developed using methods such as Finite Element Analysis (FEA) and particle hydrodynamics. These methods provide improved accuracy but are computationally intensive and are therefore unsuitable for fast real-time calculations.

As a trade-off between accuracy and execution time,this paper improves the accuracy of the Gurney model for quickly calculating the initial velocity of fragments for a cylindrical warhead. The resultant model improves the Gurney model by varying initial fragmentation velocity over the length of the warhead whilst incorporating the physical laws of momentum and energy and delivering a fast-computational speed.

The accuracy of the calculated velocity is validated against available experimental data and the execution speed of the model is compared with the original Gurney equation and a recent modified version from Huang [6]. The improved equation is then available for incorporation into active protection systems and realtime computer models.

2. Existing approaches to fragment velocity calculation

Bomb fragment behaviour depends on complex physical laws with many of the fragment variables difficult to measure accurately[7-9]. Various analytical approaches have been adopted by researchers estimating these variables. Before the advent of computers, Gurney [3] provided one of the most fruitful equation to estimate the initial velocity of fragments.

Gurney's equation focuses on the initial velocity of fragments for spherical, cylindrical and sandwich shaped casings,using the laws of conservation of momentum and energy. His equation for the initial velocity of fragments (V) in a cylindrical casing is given by:

Where V is the initial Gurney velocity,2Eis a constant that depends on the explosive material (referred to as the Gurney constant), M is the mass of the metal casing and C is the mass of the explosive material.The warhead is assumed to be detonated along the cylinder's longitudinal axis and the main limitation is there is only one initial velocity of fragments for the casing. Experimental data shows this is not accurate.

Since Gurney developed his equations authors including Charron[7],Victor[16],Kennedy[17,18],Choi[9],Gardner[19],Pearson[13], Huang [6] and Konig [20] considered improvements and investigated limitations to Gurney's equations.Huang has the most recent improvement which depends on initial work by Zulkoski[21].

As computers became more powerful, authors such as Liu [10]and Ma [11]increased the accuracy of the estimates by creating more complex physical algorithms using tools such as Finite Element Analysis (FEA) and particle hydrodynamics. Despite improved accuracy, these approaches need significant computational effort and so are unsuitable for real-time calculation(-Spranghers [12]). Additionally authors such as Fairlie [22] and Snyman [23] developed accurate but complex computer models based on the original Gurney equation. Unfortunately, these algorithms are also computationally expensive.

The Gurney equation is still used today as a good first step approximation [13] but disagrees with available experimental evidence for fragments created near to the warhead's end plates([6,7,14,15]). Also, the equation for a cylindrical warhead is onedimensional and so does not consider the velocity of fragments for the end plates of the warhead.

To overcome this weakness Victor[16]identified and advanced the work of Odinstov [24] who used a two-dimensional equation incorporating Gurney's assumptions to consider the velocity of fragments on and near to end plates. The approach used by Odinstov is similar to that of Breech [25] whose paper provides the main methodology to calculating the initial velocity of fragments developed in this paper.

As with Gurney's equation, Breech uses the conservation of energy and momentum to provide the following [25]:

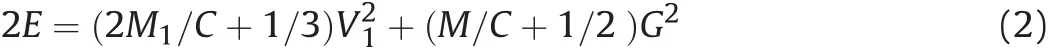
Where V1is the velocity of fragments at the detonation and nondetonation end plates, each with a mass of M1, M is the mass of the cylindrical part of the warhead,C is the mass of the charge and G is the Gurney velocity.

The right-hand side of Equation(2)contains two parts with the first part being the one-dimensional Gurney equation for an explosive charge sandwiched between two parallel plates. The second part is the one-dimensional Gurney equation for a cylindrical warhead. As with Gurney's equation, the main limitation is there is only one initial velocity of fragments for the casing and one initial velocity of fragments for each of the end plates.

The aim of this paper is to improve the accuracy of estimating the initial velocity of fragments whilst maintaining low computational overhead. It considers the explosion as a two-dimensional equation as shown by Breech and uses a physical model, similar to Gurney's and Breech's model, to estimate the initial velocity of cylindrical fragments as well as considering the kinetic energy and momentum of explosive gases.In developing Beech's equation the novel work considers the two independent parts of his equation(the velocity of end plate fragments and the velocity of cylindrical fragments) by including the ratio of pressure inside the warhead developed by Lloyd[26].

3. Derivation and analysis of new fragment velocity equations

The most common reference case for a cylindrical warhead is one that is detonated at one end of the warhead. Fig. 1 shows experimental data from Karpp, Charron (experiment number 876)and Grisaro for initial fragment velocity over the length of warheads and Table 1 provides several variables of the warheads. In this paper ‘Velocity’ (of a fragment) refers to the ‘Modulus of Velocity’. Grisaro's experimental data is from a similar configuration as Huang's so only Grisaro's data has been included in the results section of this paper.

Using experimental data this paper assumes the shape of the initial fragment velocity for end-initiated warheads is as shown in Fig.2.Different researchers use different units to measure velocity so for consistency this paper translates velocity units into mm⋅μs-1.The points A and C may change their ordinate values to create a flatter or steeper curve, depending on the initial warhead dimensions and the type of explosive charge.The thickness of the end plates will also affect the shape of the curve so for simplicity this paper assumed that the end plates are the same thickness as the cylindrical warhead.

To provide a simple model that represents the curve in Fig. 2,two second degree polynomials are used.Three points on a seconddegree polynomial are required to define the polynomial;so,for the two polynomials the three points are A,B,E and D,B,C as shown in Fig.3.The curves A,B,E and D,B,C are symmetrical about the line X/L= B and point C is at the abscissa X/L=1.The curve A,B,C can then be represented by two second degree polynomials and X/L= B defines where the curve has a maximum value (approximately 0.60-0.70 of the length of the warhead from the detonation end plate).

3.1. Initial fragment velocity

To establish the initial fragment velocities over the cylindrical part of a warhead a quadratic polynomial in the form of:

is defined where the coefficients a, b and c are to be determined.

Let X/L be the distance X of the warhead from the origin divided by the length of the warhead L. To simplify the mathematics the cylinder casing is translated by the equation x/L=X/L-B. This means the origin of the polynomials is assumed to be where X/L=B which is the maximum point of the curves in Fig. 3.

The coefficients a, b and c result in the following equation:

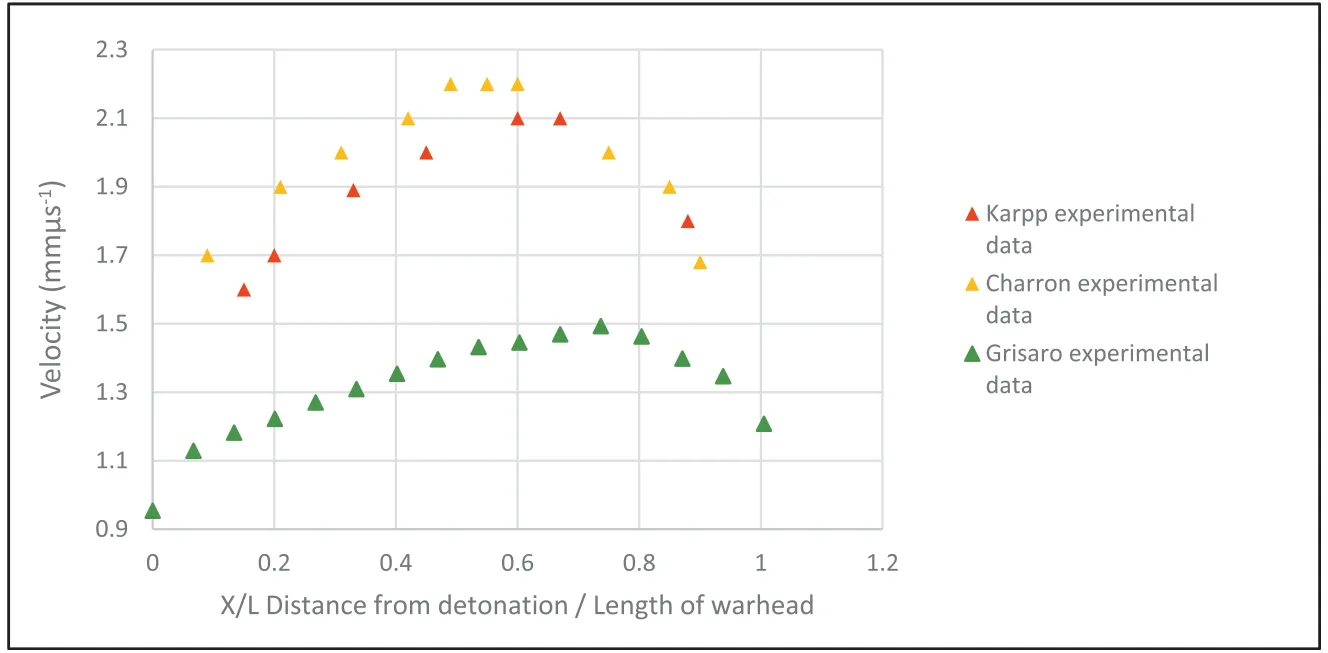
Fig.1. Cylindrical fragment velocity from experimental data.

Table 1Characteristics of the experimental data for warheads.

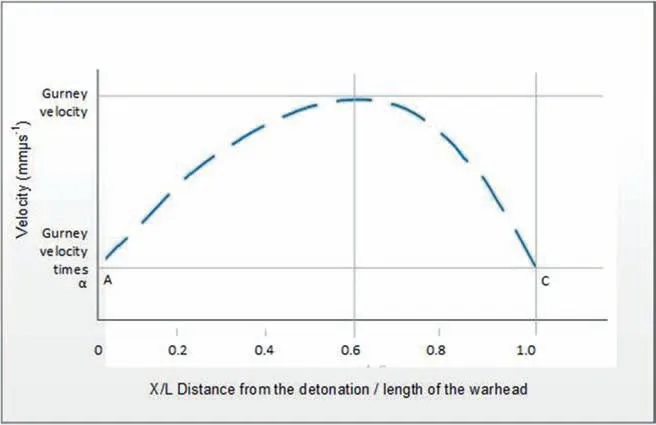
Fig. 2. Graph of experimental velocity of fragments.

Where the initial velocity at points A and C is Gα and 0 ≤α ＜=1;i.e.the velocity of fragments at points A and C is a reduction of the Gurney velocity G.Not all available experimental data indicates that points A and C have different ordinate values.If this is not the case then the value of α at point C will change to α′which means α in Equation(4),for x/L ≥0,is replaced by α’.This paper assumes that points A and C have the same ordinate values.

The velocity at point B is G,the Gurney velocity as experimental data indicates the value of the initial velocity of fragments at point B approximates to the value of the Gurney velocity. This is shown on each of the papers by Karpp [14], Charron [7], Grisaro [15] and Huang [6] where the Gurney velocity is also shown on the experimental data graphs. The experimental data also indicates that B has a value between 0.60 and 0.70. This paper uses the value of B=0.65.

3.2. Conservation of energy

Using similar physical models as both Gurney (for the onedimensional equation) and Breech (for the two-dimensional equation) the total Kinetic Energy of the Gas in the cylindrical casing is:

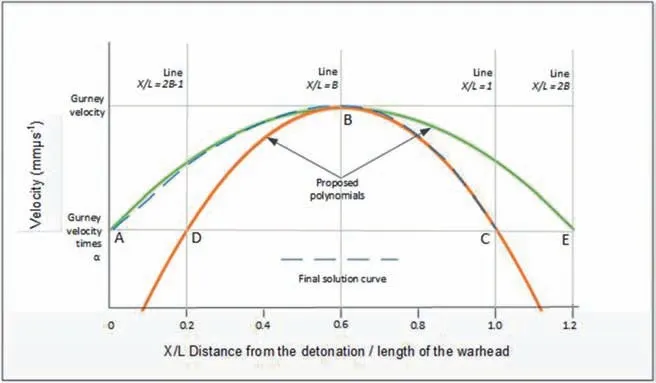
Fig. 3. Curve created from two polynomials that contains points A, B and C.

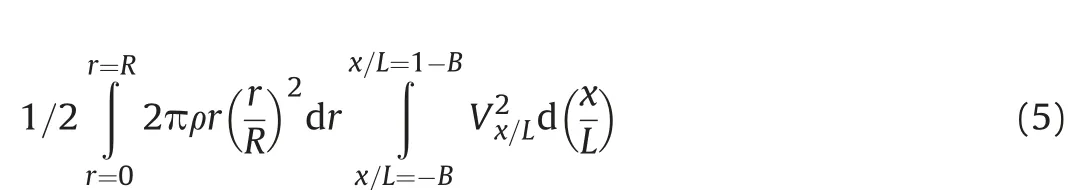
Where x/L is the dimension along the axis of the cylinder and r is in the direction of the YZ plane.Using Gurney's model the velocity at distance r from the axis is given by Vr=Vx/Lr/R,Vxis the velocity of the gas touching the casing, ρ is the density of the explosive material, ρ = C/πR2, C is the mass of the explosive charge per unit length,V2r=V2x/L（r/R）2and Vxis defined as the velocity in Equation(4).

Evaluating integrals in Equation (5) gives:

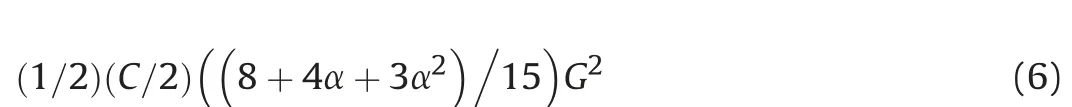
Similarly,the total kinetic energy of the cylindrical casing can be calculated using the diagram shown in Fig. 4.

The Kinetic Energy of the cylindrical casing is:

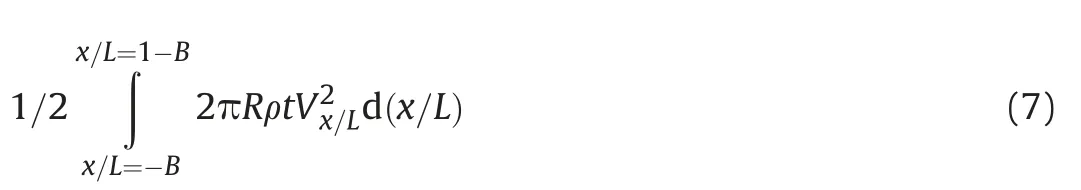
Which is equal to:

where ρ is the density of the metal casing and M is the mass of the cylinder per unit length.

Evaluating the integral gives:

Assuming the same method to calculate the cylindrical and end plate fragment initial velocity as Breech's equation the twodimensional equation linking energy (and momentum) with the energy of the explosive mass being E per unit length becomes:

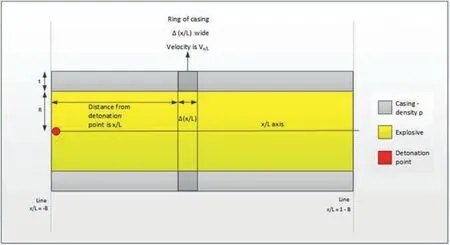
Fig. 4. Calculate Kinetic Energy of casing.

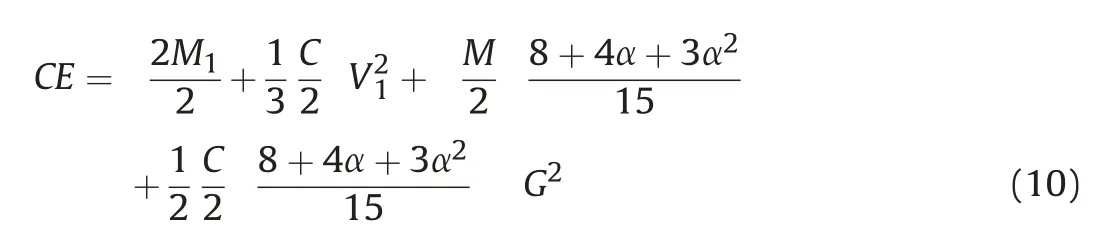
When α=1 the solution of Equation (10) reverts to Breech's equation.

The right-hand side of Equation(10)contains two parts;the first part represents the average energy in the X direction (the end plates)and the second part represents the average energy in the YZ plane (the cylindrical casing). To be consistent the physical representation of energy on the left-hand side of the equation then needs to reflect these two distinct parts for the average energy released in an explosion.

Lloyd [26] provided a means of splitting the left hand side of Equation (10). He suggested that the part of the equation that includes the ratio C/M should also include the termThis estimates the amount of the surface area of the warhead affected by the explosion by calculating the ratio of the surface area of the cylinder divided by the total surface area of the warhead.D is the diameter of the warhead and L is its length.

Using the same logic as Lloyd the surface area of the cylindrical part of the warhead, divided by the total surface area of the warhead is:

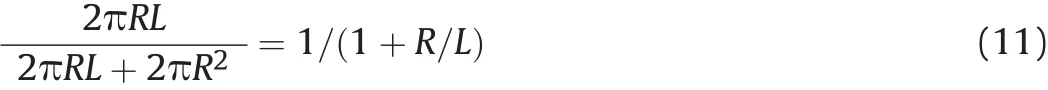
And the surface area of the end plates of the warhead,divided by the total surface area of the warhead is:

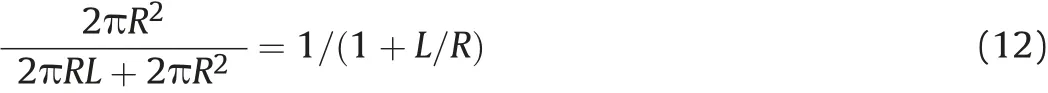
This means that Equation (10) becomes:

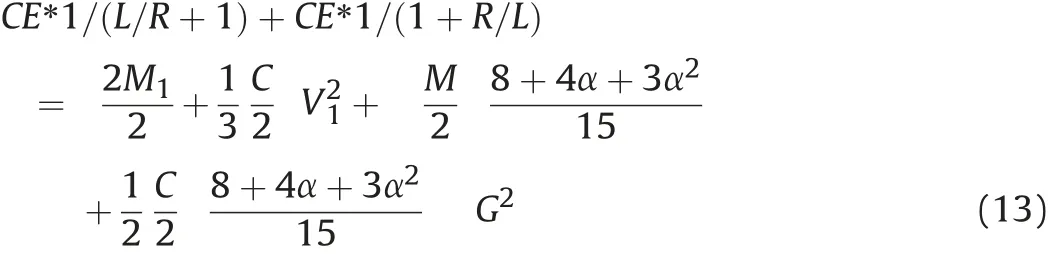
This equation now contains two distinct parts.On the left-hand side of the equation,energy in the X direction and energy in the YZ(or r) direction respectively and on the right-hand side, energy in the X direction and energy in the YZ (or r) direction respectively.

This means Equation (13) can be represented as:

For the cylindrical part of the casing(“in the r direction”)and as:

For the end plates (“in the X direction”).

3.3. The value of the “velocity coefficient” α (the reduction of the gurney velocity at the end plates)

The velocity coefficient α has a value within the range 0 ≤α ＜=1, where Gα is the value of initial velocity of cylindrical fragments next to the end plates.

The assumption used by Gurney and later by Breech about the velocity of the explosive material in the r direction (i.e. perpendicular to the axis) is given by:

Where Vris the velocity of gas, r is the distance from the axis, R is the radius of the explosive charge and G is the Gurney velocity.

This paper uses a modification of this formula to estimate the value of a.The modification assumes that the maximum expanding case fragments when the radius of the warhead is RE.As the Gurney equation is a good approximation of the initial fragment velocity(in the centre of the warhead) the density of the explosive material is reduced by （R/RE）2to maintain the form of the original Gurney equation.

Equation (16) then becomes:

From Fig.5 the velocity in the r direction at A(the end plate)is Vrwhere:

So,the value of α depends on the ratio of R/REon which there is little published information. This ratio may not be a constant but may depend on variables such as the type of explosive and the thickness of the casing. Researchers have provided a limited number of values for this ratio.However,there is experimental data from Victor [16] who mentions that the case expands by 1.6-1.8 times its original warhead radius, where the original warhead radius is equal to the explosive radius plus the thickness of the casing. Karpp [14] indicated a ratio of 1.75 for steel casings. If the value of REis 1.6 then α would be equal to 0.625.

Goto also wrote a paper investigating the fracture of explosively driven cylinders[27].The paper considers an open-ended cylinder and researches how the cylinder is affected by increases in metallic strain.The equivalent plastic strain(eps)is estimated as 0.46 which gives a value of R/REof about 0.65,using explosive LX-17 which is a mixture of TATB, (TriAminoTrinitroBenzene) and Kel-F (Poly-ChloroTriFluoroEthylene). The paper also refers to calculations by Taylor [28] who provides some estimates of R/REwith pentolite explosive. His values of R/REvary from 0.81 to 1.1.

Some of the above experimental values have ignored the expansion of the casing at point A.As point A expands the ratio of R/REwill change to R’/REwhere R’ is the expanded value at point A.More work in the underlying physics at point A is required to resolve this issue, which is beyond the scope of this work.

Grisaro provided a value for α at both end plates. For the detonation end plate, when the ratio of the length of the warhead divided by the radius ≥2,he provided a figure of 0.65[15].For the non-detonation end he provide a figure of 0.8.

The value of α=0.65 for the detonation end has been selected for this paper thereby recognising the value in Grisaro's paper and accepting the casing at the detonation end will also expand.For the value of α at the non-detonation end both the value of 0.8 (from Grisaro) and a figure of 0.65 have been considered.

4. Results

The absence of experimental or empirical data means that Equation(15)cannot currently be verified.The derived accuracy of Equations(14)and(4)is verified using two different methods.The first method is to test the accuracy of the calculation of the Gurney velocity-using Equation(14)and the second method is to compare the correlation of Equation (4) with available data.

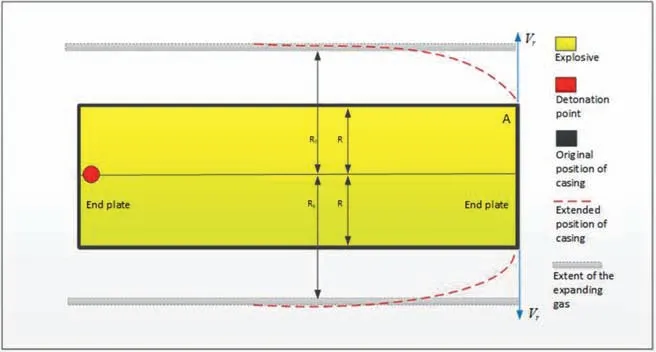
Fig. 5. The extended casing.

4.1. Gurney velocity (comparison of Equation (14) against existing data)

Table 2 is assembled from available experimental results,which unfortunately shows that some values in cited papers are not consistent and, in some cases, information is not available.Comparing the values shown in columns E and F with the values shown in columns H and I indicate large differences can be identified. This is probably caused by the difficulty in measuring variables such as the initial velocity of fragments in an explosion or the difficulty to extract data from graphs.

The values in column L are similar to the values shown in column H apart from the Waggener [29] experimental values. As the Waggener values are for centre detonated warheads some differences should be expected. Otherwise this suggests column L is a good representation of the Gurney velocity, using a more detailed method (Equation (14) to evaluate it) and better results could be available with an improved value of α.

4.2. Correlation between Equation (4), the velocity distribution equation, and experimental data

The accuracy of Equation (4) is checked against experimental data provided by Karpp [14], Charron [7], and Grisaro [15]. The experimental data is relevant to warheads being detonated at an end plate.

The results are set out in Fig. 6 with the calculated data for the revised Gurney equation being compared to experimental results.The correlation coefficient used to determine the “goodness of fit”between the experimental and calculated velocities is Pearson's coefficient as outlined in Rodger's paper[30].This coefficient has a value between -1 and 1 where the value of 1 indicates an exact positive correlation and-1 indicates an exact negative correlation.There is good correlation between experimental and calculated results. In each of the experimental results the correlation coefficient is greater than 0.85. This shows the revised Gurney equation accurately follows experimental results.

The results using Equation (4) show the calculated fragment velocities are an improvement to the Gurney velocity.Significantly,this approach allows for a variation in fragment velocity over the length of the warhead.

The result of this work is the production of three equations;Equation (4) - to calculate variable fragment velocities, Equation(14)-to calculate a revised Gurney velocity and Equation(15)-to calculate the velocity of end plate fragments.

4.3. Comparison with Huang's equation

As an additional verification of Equation(4)the equation used in the most up to date paper(Huang's paper[6])was compared withexperimental data and the results from Equation (4). Fig. 6 shows the three sets of data.

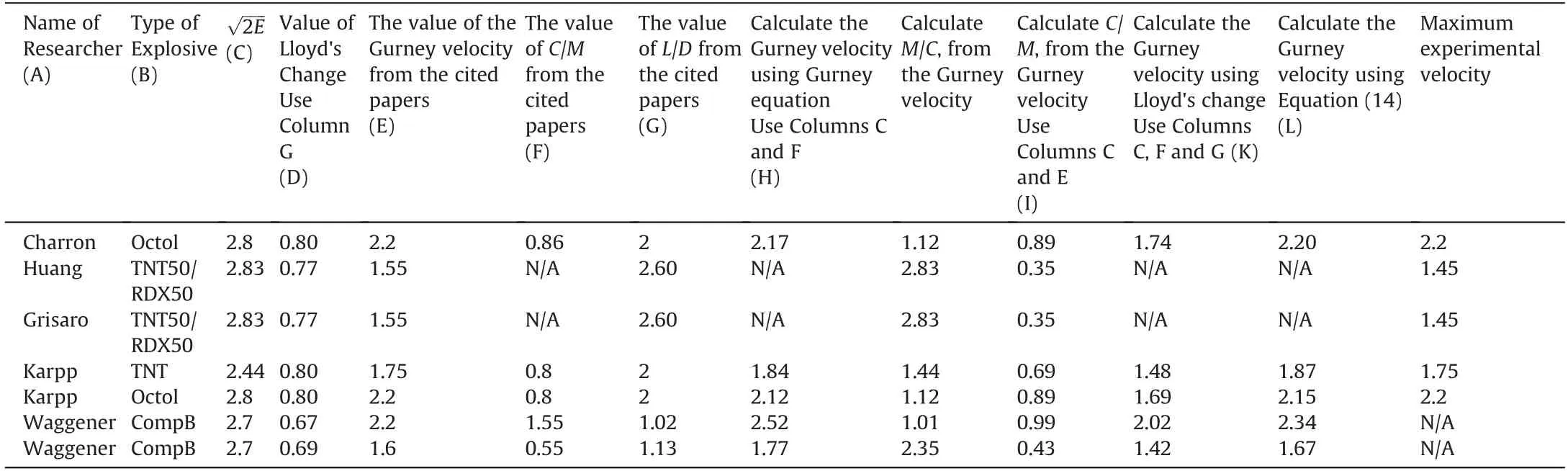
Table 2Calculations of the Gurney velocity taken from some researchers.

Fig. 6 shows that the three sets of data are similar over a large proportion of the warhead. Huang's equation was created using initial velocity data,including the value of the initial velocity at the two end plates,and fitting this data to an exponential curve using least squares of the distance between the curve and experimental data. It is therefore expected that the resultant curve would accurately follow experimental data.

Equation (4) was compared with Huang's equation using the sum of the absolute differences between the experimental data and the two curves. The distances for the two curves were almost identical, which indicates that Equation (4) and Huang's equation have similar results. The “two sample Kolmogorov-Smirnov goodness of fit test” [31], also identifies that Equation (4) and Huang's equation are similar. However, there are some variations; Fig. 7 shows that Huang's equation shows closer correlation at the nondetonation end whereas Equation (4) is closer at the detonation end. This is probably caused by the value of α being greater at the non-detonation end of the warhead.

4.4. Comparison with Kong's paper

Kong published a paper measuring the velocity of fragments for a cylindrical explosion with strengthened end plates, which can influence some or all of the results [32]. The dimensions of the cylinder include a cylindrical casing 160 mm long,with an internal radius of 110 mm and a casing thickness of 6 mm.The weight of the casing is 4.1 kg and the TNT charge has a weight of 1.9 kg.Gurney's constant for TNT is assumed to be 2.44 mm⋅μs-1.This gives a value of the Gurney's velocity for fragments formed in the cylindrical part of the explosion of 1,496 m s-1and a value of the enhanced Gurney velocity of 1,305 m s-1. Kong provides a value for the velocity of fragments between the middle of the cylinder and the nondetonation end plate of about 1,400 m s-1. The value of α for fragments at Kong's sensor position 5 is estimated at about 0.82(approximately 1150/1400).As the sensors on the cylindrical part of the casing are equally spaced the value of α at the detonation end plate is estimated to be approximately 0.65. The value of α for fragments at Kong's sensor position 8 is estimated at about 1.0(approximately 1400/1400). This provides a value of α at the nondetonation end plate to be approximately 0.85, which agrees with Huang's experiment but not with Charron's or Karpp's experiments.

A comparison of the velocity of fragments at the end plates is more difficult to determine because the weight of the end plates in Kong's experiments need to be known. This comparison has therefore not been included.

4.5. Computer execution times

An estimate of the additional computer execution time required to run the revised Gurney equation is obtained by implementing the Huang experimental data in MATLAB and executing the revised Gurney equation 50,000 times and logging the time taken to execute 1000 cycles. The average execution time for one cycle is calculated to be approximately 35.44μs.

The algorithm is compared with the speed of the equation shown in Huang's paper [6], using the formula:

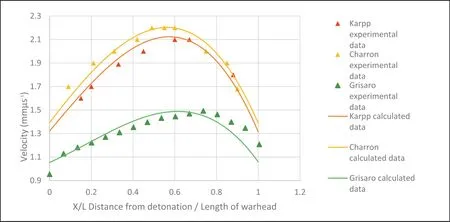
Fig. 6. Graphical results of experimental and calculated data.

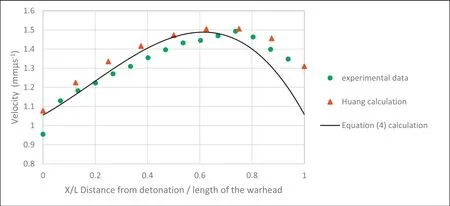
Fig. 7. Experimental Huang data compared to calculated Huang and Equation (4) data.

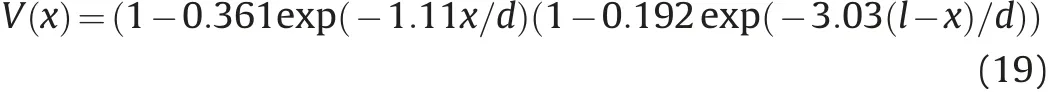
Where V(x)is the correction at position x and x is the distance from the detonation end, d is the diameter of the charge and l is the length of the casing. Huang's equation gives an average execution time of 0.4002 s, over 5 runs. This means the additional time to calculate the velocities is 40.02μs.

This shows the revised Gurney velocity equation, with 15 elements, is comparable to a similar equation. It is marginally slower than the original Gurney equation but by less than 1/10 of a millisecond.

4.6. Conclusion

This study presents three new equations. An equation to calculate the initial velocity of fragments on a cylindrical end plate-Equation (15), an equation to calculate the maximum initial velocity of fragments on a cylindrical casing (“the Modified Gurney velocity” Equation (14) and an equation to calculate the initial,variable fragment velocity for a fragment on a cylindrical casing -(Equation (4)).

The cylindrical Gurney equation,Equation(14)is compared with the original Gurney equation initially using seven sets of experimental data. Two sets of data contain insufficient variables which make their results indeterminate. The remaining five sets of data provide similar results to the original Gurney equation.However,as this is to be extracted from experimental graphical data, some of the extracted data may be inaccurate. For this reason, the improvement(or reduction)of the modified Gurney equation with the original is not enumerated.

The modified Gurney equation, Equation (4), is compared with three sets of experimental data. The results of this comparison present a value for the correlation coefficient greater than 0.85,which indices a close positive correlation between the revised Gurney equation and experimental data. The original Gurney equations when compared with experimental results have correlation coefficients estimated at less than 0.20.This indicates there is little correlation between the original Gurney equation and experimental results and demonstrates that the revised Gurney equation offers an improvement over the original.

The original Gurney equation,which provides quick and simple results is still a reasonable first step that delivers the maximum initial fragment velocity of a warhead which may be suitable in some models.However,it is preferable to use the modified Gurney equation for Active Protection Systems and simulations that need many real time results because it is more accurate than the Gurney equation and nearly as quick to compute.

Although Equations(4),(14)and(15)give better results than the original Gurney equation there are some issues. There is a possibility that the assumed value of R/REis incorrect.This is believed to be attributed to the reduced action of the pressure of the gases close to the end plates.However,little published information could be found concerning either the end plate fragments velocity or the expansion of the casing next to the end plates.Further work is also needed to determine the impact of detonating the warhead at one of the end plates,especially concerning the distribution of fragment velocity over the end plates.

Acknowledgement

We have received partial funding from DSTL.