半序概率度量空间中混合单调算子的耦合不动点定理

朱奋秀

(湖北经济学院法商学院， 湖北 武汉 430205)

1 引言与预备知识

近年来，半序方法成为研究非线性算子不动点问题主要的方法，然而在概率度量空间中利用半序方法研究混合单调算子不动点问题的文献较少.1976 年，Caristi J 利用泛函在度量空间中引入了一个半序并得到几个不动点定理；文献[4]在概率度量空间中引入半序，讨论了序压缩算子的不动点理；文献[5]讨论了在半序概率度量空间中的一类增算子的不动点定理，并得到一类非线性算子方程的可解性理论；文献[6]讨论了概率度量空间中序压缩算子对的重合点定理；文献[7]讨论了在半序概率度量空间中满足一定条件的形如Lx ＝N(x，x)，一类非线性算子方程的可解性问题. 下面将在概率度量空间中引入半序关系研究一类混合单调算子，在满足两点压缩和拉伸条件下，得到算子的耦合不动点的存在性.

一些关于半序概率度量空间的基本概念和记号见文献[2 -15].

设(E，F，Δ)是Menger 概率度量空间，且t-范数Δ 满足Δ(t，t)≥t，φ:E→R 为泛函，定义E 上的″≤″为，对任意的x，y∈E，x ≤y⇔∀ε ＞φ(x) -φ(y)，∀λ＞0，都有Fx，y(ε) ＞1 -λ，可以验证″≤″为(E，F，Δ)上的半序关系，称此关系为由φ 导出的半序.

设 x0， y0∈E 且 x0≤y0， 称[ x0， y0] ＝为序区间

定义1 设(E，F，Δ)是Menger 概率度量空间，其中的半序由泛函φ 所导出，设算子A:E ×E→E，若对任意的x1，x2，y1，y2∈E，当x1≤x2，y2≤y1时，有A(x1，y1)≤A(x2，y2)，则称A 为混合单调算子.

引理1[3]设″≤″是概率度量空间(E，F，Δ)上由φ 导出的半序，若x ≤y，则φ(x)≥φ(y).

2 主要结果

定理1 设(E，F，Δ)是Menger 概率度量空间，且t-范数连续且满足Δ(t，t)≥t，φ:E→R 为连续泛函，″≤″是由φ 导出的半序.设x0，y0∈E，x0≤y0，D ＝[x0，y0].又设A:D ×D→E 是关于″≤″的混合单调算子，且x0≤A(x0，y0)，A(y0，x0)≤y0. 则算子A 存在耦合不动点，使得

证明 设C ＝{(x，y)∈D ×D:x0≤x ≤A(x，y)，A(y，x)≤y ≤y0}，显然(x0，y0)∈C，于是C 为非空集合，在C 上定义关系如下:

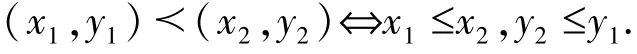
易证(C，≺)为半序空间，下面证明(C，≺)有极大元.令{(xμ，yμ)}μ∈J是(C，≺)的任一全序子集，其中J 为定向集，即μ，ν∈J，μ ≤ν 当且仅当(xμ，yμ)≺(xν，yν).

对任意μ，ν∈J，μ ≤ν，有xμ≤xν≤y0，x0≤yν≤yμ，因此可证

φ(xμ)≥φ(xν)≥φ(y0)，φ(yμ)≤φ(yν)≤φ(x0)，{φ(xμ)}μ∈J，{φ(yμ)}μ∈J是R 中的单调有界网，从而{φ(xμ)}μ∈J，{φ(yμ)}μ∈J收敛.

因{φ(xμ)}μ∈J收敛，故对∀ε ＞0，∃N，对任意的N ≤μ ≤ν 有φ(xμ) -φ(xν) ＜ε/2，又由xu≤xv，都有∀λ ＞0，Fxν，xμ(ε/2) ＞1 -λ，即 xμ{ }μ∈J是E 中的τ -Cauchy 列，由Menger 概率度量空间的完备性，设{ xμ}μ∈J收敛于x∗，对任意固定的μ∈J.因此有对ε ＞0，当ν≥μ 时有

又由φ 连续性limv(φ(xμ) -φ(xν)) ＝φ(xμ) -φ(x∗) ＜ε/2 ＜ε，对λ ＞0 都有

从而有xμ≤x∗，∀μ∈J.同理可证 yμ{ }μ∈J收敛于y∗，且有y∗≤yμ，∀μ∈J.

显然x0≤xμ≤x∗≤y0，x0≤y∗≤yμ≤y0，由算子A 的混合单调性有

由xμ≤A(x∗，y∗)⇔∀ε ＞＞φ(xμ) -

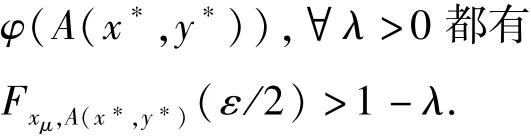
又由φ 连续性，limμ(φ(xμ) -φ(A(x∗，y∗))) ＝φ(x∗) -φ(A(x∗，y∗)) ＜ε/2 ＜ε.

由Menger 的广义三角不等式得

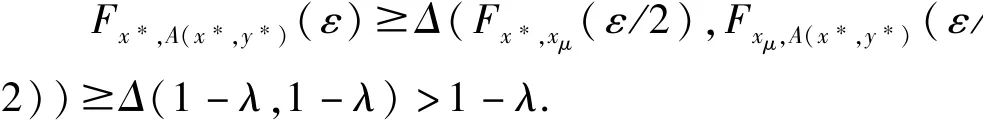
从而有x∗≤A(x∗，y∗)，同理可证A(y∗，x∗)≤y∗，所以(x∗，y∗)∈C，且(xμ，yμ)≺(x∗，y∗)，∀μ∈J，因此(x∗，y∗)是{(xμ，yμ)}μ∈J是一个上界，应用zorn 引理，(C，≺)有极大元∈C，下面证明(A

注1:定理1 与其他相关文献相比，在概率度量空间中引入混合单调算子，并在两点压缩条件下证明了其耦合不动点定理.

下面将证明在半序概率度量空间中，混合单调算子在两点拉伸条件A(x0，y0)≤x0，y0≤A(y0，x0)下的耦合不动点定理.证明方法仿定理1.

定理2 设(E，F，Δ)是Menger 概率度量空间，且t-范数连续且满足Δ(t，t)≥t，φ:E→R 为连续有界泛函，″≤″是由φ 导出的半序.设x0，y0∈E，x0＜y0，D ＝[x0，y0].又设A:D ×D→E 是关于″≤″的混合单调算子，且A(x0，y0)≤x0，y0≤A(y0，x0). 则算子A 存在耦合不动点，使得

证明 仿定理1 证明设C ＝{(x，y)∈D × D:A(x，y)≤x ≤x0，y0≤y ≤A(y，x)}，显然(x0，y0)∈C，于是C 非空，在C 上定义关系如下:

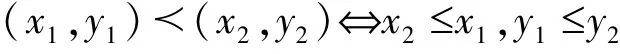
易证(C，≺)成半序空间，下面证明(C，≺)有极大元.令{(xμ，yμ)}μ∈J是(C，≺)的任一全序子集，其中J 为定向集，即μ，ν∈J，μ ≤ν 当且仅当(xμ，yμ)≺(xν，yν).

对任意μ，ν∈J，μ ≤ν，有xν≤xμ≤x0，y0≤yμ≤yν，因此有

φ(xν)≥φ(xμ)≥φ(x0)，φ(y0)≥φ(yμ)≥φ(yν).

又φ 有界，故{φ(xμ)}μ∈J，{φ(yμ)}μ∈J是R 中的单调有界网，从而{φ(xμ)}μ∈J，{φ(yμ)}μ∈J收敛，仿定理1 可证 xμ{ }收敛于x∗， yμ{ }收敛于y∗，且x∗≤xμ≤x0，y0≤yμ≤y∗，

由算子A 的混合单调性有

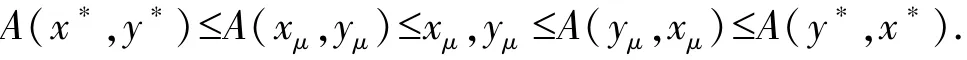
又由φ 连续性，limμ(φ(A(x∗，y∗)) -φ(xμ)) ＝φ(A(x∗，y∗)) -φ(x∗) ＜ε/2 ＜ε.

由Menger 的广义三角不等式得

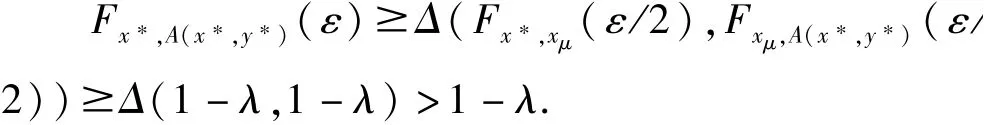
从而有A(x∗，y∗)≤x∗，同理可证y∗≤A(y∗，x∗)，所以(x∗，y∗)∈C，且(xμ，yμ)≺(x∗，y∗)，∀μ∈J，因此(x∗，y∗)是{(xμ，yμ)}μ∈J是一个上界，应用zorn 引理，(C，≺)有极大元∈C，下面证明(A

由算子的混合单调性，

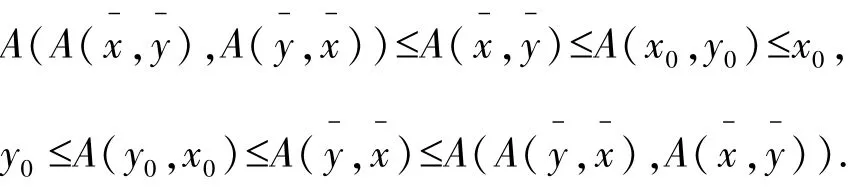
注2:文中定理1，定理2 在概率度量空间中通过泛函引入半序，且在两点压缩条件和两点拉伸条件下，得到混合单调算子的耦合不动点定理，且与其他文献[4 -5，7]相关结论相比弱化了算子A 的连续性，使用与构造迭代序列完全不同的方法，证明其耦合不动点定理.