基于ANSYS的塔器自振周期计算

李俊儒

(中石化宁波工程有限公司，上海 200030)

自振周期(或频率)是塔器设计中确定风载、地震载的重要参数，它直接影响着塔器动力计算结果的精度。对于常见的自支承式塔，在确定其自振特性时，可视为一端固定、另一端自由的悬臂梁【1】，从而将问题转化为求解悬臂梁的线性振动。

目前，NB/T 47041—2014《塔式容器》【2】中自振周期主要的计算方法包括：1)弹性连续体解析法，即NB/T 47041中的式(19)，为精确解法，但只适用于等截面塔；2)集中质量法，即NB/T 47041中的式(16)，需要事先假定振型函数，对于复杂结构和高振型计算困难；3)矩阵迭代法，即NB/T 47041中的附录B，求解高振型时通常采用此法，计算相对复杂。

而有限元法汲取了集中质量法与假设模态法的优点，它将实际结构划分为一系列离散单元，单元之间通过节点连接，然后对这些单元的组合体进行求解【3】。有限元法可根据塔器的截面变化、加载及支座等情况，划分单元并赋予其相应的截面特性、材料属性以及施加约束、载荷，是不等截面塔器自振特性分析的有力工具。

本文采用有限元软件ANSYS分析了《NB/T 47041—2014<塔式容器>标准释义及算例》(以下简称“标准算例”)中例题1～例题4所示的4台不同类型塔器的自振特性，并与NB/T 47041中的计算方法进行了比较，着重分析了不等截面塔器自振周期及振型函数。

1 ANSYS分析过程

ANSYS分析的过程主要包括：定义单元类型、截面特性、材料属性，建立模型，赋予模型材料属性和划分网格，施加约束和载荷，求解，以及后处理。

采用ANSYS 15.0的2节点管单元pipe288划分模型网格。ANSYS帮助文件的说明显示，pipe288单元基于铁木辛柯梁理论，考虑了梁的剪切变形，适用于细长、中等粗短的管结构。与实体单元、壳单元相比，管单元的建模、网格划分都较为简单，便于工程技术人员掌握和运用。

建模时，首先按塔器的几何尺寸及分段数创建关键点，再由关键点生成直线即可。对于线模型的网络划分，只需指定单元长度或单元数。需要指出的是，集中质量法、矩阵迭代法的分段数与自由度个数对应【4】，ANSYS求解中的自由度个数与网格数目对应，而不是与模型中的分段数对应。另外，借助ANSYS参数化设计语言实现了仿真全过程的参数化，避免了繁琐的界面操作，便于进行分析研究。

另外，ANSYS计算还应注意【3】：

1) 在定义单元属性时，需要将单元行为方式定义为三次函数，以提高精度。

2) 在确定材料属性的密度时，需要将操作质量m0折算成塔体等效密度ρe，即(公式中的符号解释，除特殊注明外，均与文献【2】一致，下同)：

式中：ρe——塔体等效密度，kg/m3；

V——塔器金属壳体体积(计算时壳体厚度取名义厚度，与标准算例保持一致)，m3。

3) 对于没有其他支撑的自支承式塔器，模型底部应施加全约束。而若只是求解自振特性，无需施加其他载荷。

4) 模态提取方法设为分块兰索斯法(Block Lanczos)，模态提取阶次及扩展阶次本文设为6阶。

2 等截面塔器的计算

2.1 例题1

标准算例中的“例题1”为φ1 400 mm×18 900 mm等直径泡罩塔，高径比H/D=13.5<15，且H<20 m，根据NB/T 47041中7.5.4的规定，可以不考虑高振型。按NB/T 47041式(19)计算其基本自振周期T1：

频率f1=1/T1=1.429 Hz。

ANSYS计算的主要参数为 ：截面特性中壁厚取壳体有效厚度0.005 m；设计温度下材料的弹性模量Et为1.97×1011Pa，泊松比ν取0.3；等效密度ρe为56 701 kg/m3;V为圆筒的体积，(圆筒内径为1.400 m，厚度0.005 m，高度18.900 m)；忽略封头等零部件，与标准算例一致。由2个坐标分别为(0.0,0.0,0.0)、(0.0,18.9,0.0)的关键点创建直线，因为操作质量沿高度均匀分布，因此模型无需分段；网格数设为100。

式中：i——第i阶的相对误差；

fi——按NB/T 47041中相应公式计算得到的第i阶自振频率，Hz。

2.2 例题3

标准算例中的“例题3”为φ2 400 mm×73 300 mm 的等直径等厚度浮阀塔，高径比H/D=30.4>15，且H>20 m，需考虑高振型。标准算例按NB/T 47041附录B(即矩阵迭代法)计算其前3阶自振周期，有T1=3.828 9 s，T2=0.610 9 s，T3=4.541 3 s，则频率分别为f1=0.261 Hz，f2=1.637 Hz，f3=4.541 Hz。

图1 例题1振型

ANSYS计算的主要参数为：壁厚取有效厚度0.019 m；Et=1.95×1011Pa，ν=0.3，ρe=22 168 kg/m3；由(0.0,0.0,0.0)、(0.0,73.3,0.0)2个关键点创建直线，模型不分段；网格数设为200。

ANSYS与NB/T 47041附录B的计算结果非常接近，各阶最大相对误差不超过1.20%，见表1。

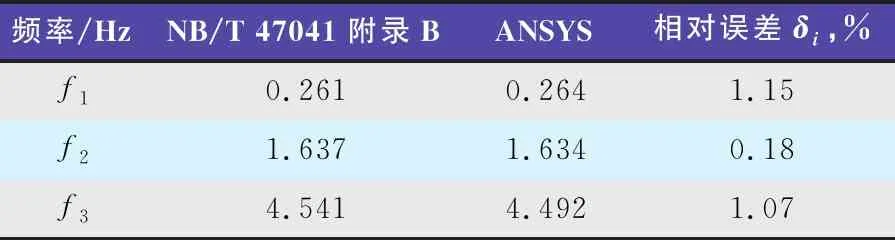
表1 例题3计算结果比较

图2 例题3振型

3 不等截面塔器的计算

3.1 例题2及其模型改进

标准算例中的“例题2”为φ800 mm/φ400 mm/φ800 mm×18 400 mm的不等直径填料塔，高度方向上截面尺寸变化较大，塔高H<20 m，无需考虑高振型。标准算例按NB/T 47041的式(16)(即集中质量法)计算其自振周期T1=1.29 s，即f1=0.775 Hz。而本文采用ANSYS计算得到的基本自振频率为1.147 Hz，两者相对误差达48%，误差较大，需要进一步分析。

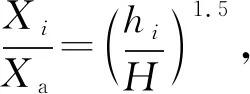
对于振型函数假定困难的塔器，还可采用矩阵迭代法计算自振周期。与集中质量法相比，矩阵迭代法的计算结果与主振型函数并不直接相关，准确度也较高【6】。但矩阵迭代法计算量大，手算困难，通常借助计算机程序进行。本文将例题2的塔器“加高”，φ400 mm部分由8 600 mm加长至10 400 mm，塔器总高为20 200 mm，其余尺寸不变，如此便可借助SW6软件进行矩阵迭代法的计算【7】。

本小节采用改进的“例题2”塔器模型，比较了集中质量法、ANSYS有限元法、矩阵迭代法在自振周期计算中的运用。

3.1.1 NB/T 47041的集中质量法

运用集中质量法计算“改进后的例题2塔器模型”的自振周期，参数见表2。

表2 改进的例题2塔器自振周期计算

由表2有：

则

0.035 mm/N即为顶端作用单位力的变截面梁的位移【1】。

按NB/T 47041的式(16)计算得到的基本自振周期为：

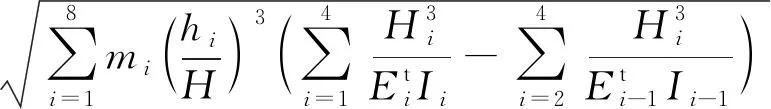
基本自振频率为0.539 Hz。

3.1.2 ANSYS模态分析

ANSYS计算主要参数为：壁厚取各段有效厚度；Et=2×1011Pa，ν=0.3；创建9个关键点并生成8条直线，分段设置截面特性、等效密度ρ，见表2；网格长度设为0.01 m，节点共计2 021个，其中1号节点为坐标原点。

图3 改进后的例题2的振型

3.1.3 由ANSYS提取振型函数的集中质量法

在ANSYS的后处理器中可提取各节点的位移，设塔器的一阶振型函数为：

式中：Xi——节点i在x轴方向上的位移，mm；

Xa——最大位移，mm。

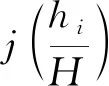
相关系数R2=1。

从图4可以看出，ANSYS计算得到的振型函数，与NB/T 47041集中质量法所假设的振型函数相差较大。

图4 振型函数

根据集中质量法的能量相等原理【1】，对于拟合得到的多项式振型函数，基本自振周期计算式为：

按表2的分段方法，进行新振型函数周期计算，其中间计算结果见表3。

表3 新振型函数计算周期的中间计算结果

3.1.4 结果比较与分析

另外，借助SW6软件进行了矩阵迭代法的计算，各种方法的计算结果列于表4。

表4 各方法计算结果比较

对于一阶自振频率，由表4可以看出：

1) ANSYS模态分析结果，与采用ANSYS振型函数的集中质量法，有30%的误差。

这是因为集中质量法中自由度个数与分段数对应，段数越多计算越准确【8】，这个数目要远小于ANSYS的网格数(或自由度个数)。可以推断，若增加分段数集中质量法的计算结果将与ANSYS 数值解趋近。

2) 而采用ANSYS振型函数的集中质量法，与矩阵迭代法计算结果误差为3.1%，两者较为接近，和ANSYS模态分析的误差也在25%左右。与集中质量法类似，矩阵迭代法的精度同样与分段数有关，SW6以1 m为一段【7】，而本小节ANSYS 计算中的单元长度为0.01 m。

3) NB/T 47041式(16)计算所得的自振频率是几种方法中最小的，即周期最大，这对于抗震设计等是偏于不安全的。原因在于，式(16)所采用的振型函数是不准确的。

3.2 例题4

标准算例中的“例题4”为φ1 400 mm/φ1 200 mm×48 000 mm的不等直径等厚度浮阀塔，高径比H/D>15，且H>20 m，需要考虑高振型。标准算例按NB/T 47041附录B(矩阵迭代法)计算其前三阶自振周期为T1=2.00 s，T2=0.42 s，T3=0.15 s，对应的频率分别为f1=0.5 Hz，f2=2.38 Hz，f3=6.67 Hz。

标准算例将该塔器分为12段(见标准算例的表4-1)，但标高14 000～18 500 mm(即第4、5段)、标高31 000～39 000 mm(即第8、9、10段)的操作质量、截面特性一样，可以分别合并成一段，本文ANSYS模型中将其分为9段。

ANSYS计算中主要参数为：壁厚取各段有效厚度；Et=1.94×1011Pa，ν=0.3；创建10个关键点并生成9条直线，分段设置截面特性、等效密度ρe；网格长度设为0.01 m。

ANSYS与NB/T47041附录B的计算结果及其相对误差见表5，前两阶误差较小，第三阶误差为5.77%。

表5 例4计算结果比较

图5 例题4振型

4 结语

对于《NB/T 47041—2014<塔式容器>标准释义与算例》中例题1～例题4的4台塔器自振周期(或频率)对比计算有：

1) 对于等截面塔器(例题1、例题3)，ANSYS模态分析与弹性连续体解析法、矩阵迭代法的相对误差较小，最小0.18%，最大不超过1.20%；

2) 对于截面变化不大的不等直径塔器(例题4)，ANSYS与矩阵迭代法在前三阶的相对误差分别为-1.60%、2.14%和5.77%；

3) 对于截面变化较大的不等直径塔器(例题2及其改进模型)，ANSYS与集中质量法、矩阵迭代的误差均较大；

将例题2塔器“加高”至H>20 m， 以便借助SW6进行矩阵迭代法的计算， 并全面比较了ANSYS 模态分析、 集中质量法、 矩阵迭代法， 发现：

a) 提取ANSYS模型中各节点位移，整理后拟合得到新的振型函数，该振型函数与NB/T 47041假定的振型函数有较大差异；

b) 在集中质量法中运用“新的振型函数”后，计算得到的塔器自振周期，与矩阵迭代法计算得到的结果误差较小(3%左右)；

c) 矩阵迭代法及采用了“新的振型函数”的集中质量法，与ANSYS模态分析均有较大误差。

这3种方法都是将具有无限自由度的实际结构简化为多自由度体系，对于截面变化较大的塔器，需要更多的自由度数目，可以认为，ANSYS的计算是更为准确的。

综上所述，ANSYS模态分析对塔器自振周期的计算是准确的、可靠的，并且容易掌握。虽然有限元模态分析法未纳入NB/T 47041塔式容器标准，但仍可作为塔器抗振设计的参考方法，尤其是对于变截面塔器。