基于遗传算法的钢板罩退工序生产调度优化

付豫金，袁林艳

（1.中国空空导弹研究院，河南 洛阳471000；2.滨海新区塘沽浙江路小学，天津 滨海300450）

0 引言

近年，企业生产调度问题越来越得到研究者的注意，从最早的组合优化、数学规划等方法被引入，到排队论、控制理论被用来解决生产调度问题，生产调度研究得到了快速发展，但随着研究问题的复杂度不断提升，精确求解法已经很难取得理想结果，启发式算法和智能算法被引入到调度问题研究中。研究范围也从传统的离散型企业扩展到流程型企业。其中，针对钢铁行业的研究逐渐得到重视。

钢铁产业中，薄板生产因技术含量高、附加值高、用途广泛的原因，成为钢铁制造中的一项核心产业。薄板生产调度问题成为钢铁产业此类问题研究中的重点，但钢板生产调度问题属于一种混合车间调度问题，即涉及具有流程型特征的连续加工，又包含批次生产等多种生产因素。薄板生产工艺过程一般包括转炉炼钢、精炼、连铸连轧、热轧、酸轧、罩退、平整和镀锌工序[1]，其中转炉炼钢、精练、连铸连扎属于连续加工过程，热轧、酸轧、罩退、平整和镀锌工序属于批次加工。但罩退工序又涉及产品分类加工问题，包含产品约束、设备约束和批次约束，是薄板生产调度问题中最复杂，最核心的部分。

针对钢铁企业的调度问题研究多集中在精炼、连铸等液体加工工序阶段，针对酸轧、罩退等固体加工工序的研究相对较少。如唐立新对薄板生产彩涂工序调度问题进行了研究，将动态规划算法与禁忌搜索算法结合起来，对问题进行了求解[2]。Wang和Tang运用禁忌搜索算法解决了热轧工序的组批和调度问题[3]。而针对罩退工序调度问题，以往研究只针对工艺约束进行了考虑[4]，没有充分考虑罩退工序生产过程中的其他因素。还有一些学者针对罩退工序的调度问题，采用了仿真、聚类分析和紧急搜索算法等方法进行了求解[5-8]。

针对以往研究未能充分考虑罩退工序实际生产中面临的多种约束问题，本文以钢板生产罩退工序为切入点，将罩退工序实际生产中具有的设备约束、产品约束、时间约束和批次约束纳入研究范畴，构建了基于多种约束的数学模型，并通过遗传算法进行求解，验证模型及算法有效性，为企业生产调度提供新的思路和方法。

1 问题描述

罩退工序是罩式退火工序的简称，是指将钢卷放在炉台上，扣入加工内罩，在进行密封检查和预吹扫后，扣入加热外罩，进行相应的退火路线操作。钢铁薄板生产中，罩退工序是典型的混型生产工序，不同规格的产品组成一个生产批次加工，因此同一批次不同规格的产品具有相同的开始时间和结束时间。同一批次产品具有同样的工艺要求，主要包括设备要求、产品厚度要求、时间要求。设备要求是指同一批次钢卷宽度叠加后不会高于罩退炉的高度，厚度要求指同一个批次的产品应具有相同的厚度属性。厚度一般分为三种规格，即小于0.6 cm、大于3 cm和处于两者之间的厚度。时间约束是指，由于同一批次钢卷特征不同，因此加工时间不同，罩退工序的时间必须满足同一批次中所有钢卷的时间要求。罩退工序调度问题示意图如图1所示。

图1 罩退工序调度问题流程图

罩退工序的调度问题是典型的混型生产调度问题，首先需要确定分批，将产品划分为不同的批次，而后需要确定某一批次产品的加工设备，并确定同一设备不同批次间的加工顺序，是典型的NP难题[4]。本文针对罩退工序，综合考虑工艺、产品和时间约束，构建数学模型，并通过遗传算法进行求解。

2 数学模型

通过罩退工序流程及约束研究，构建以最小订单加权时间为目标函数的罩退工序数学模型，具体参数设置及模型如下：

参数：

M——随机的很大的一个常数（M→+∞）

N——罩式退火炉的集合

J——钢卷的集合

Pj——钢卷j的加工时间

TR——从酸轧工序到罩退工序的运输时间

F——类的集合

Jf——类中f的钢卷的集合

Dj——钢卷j的厚度所属的属性

WIj——钢卷j的宽度

HE——罩式退火炉的高度

O——订单的集合

Fo——订单o中的类的集合

Wo——订单o的权重

Jj——钢卷j在酸轧工序的完成时间

1变量：

Jj——钢卷j的完成时间

2

Rin——0-1变量，等于1时表示钢卷i在设备n上进行加工，等于0时则不是

Qij——0-1变量，等于1时表示钢卷i在钢卷j之前进行加工，等于0时则不是

Sij——0-1变量，等于1时表示钢卷i和钢卷j一起进行加工，即属于同一个并行批次，等于0时则不是

数学模型：

模型中，（1）为本模型的目标函数；约束（2）-（6）表示是否为同一批次以及相应的钢卷加工顺序的逻辑约束；（7）表示每一个钢卷只能选择一个罩式退火炉进行加工；约束（5-8）是关于选择在同一时间同一罩式退火炉加工的钢卷的加工时间的约束，其加工时间为所含钢卷的固有加工时间的最大值；约束（9）是关于每一个钢卷在罩式退火工序的完成时间的约束；约束（10）-（11）是关于同一批次的钢卷之间的厚度约束和宽度约束，即厚度要一致，宽度之和不能大于罩式退火炉的高度；约束（12）-（13）表示类和订单的完成时间，皆为所含钢卷的完成时间的最大值；约束（14）是关于0-1变量的约束。

3 算法实现

钢板罩退工序的生产调度问题属于NP难题，智能算法是求解NP难题的重要方法。由于本文研究问题涉及约束及因素较多，因此需要选择即具有较好的灵活性又能充分表达生产因素的算法。本文采用遗传算法进行模型的求解，一方面，遗传算法能够很好地表达各种生产因素和约束，同时具有良好的稳定性及时效性。

3.1 染色体的编码与解码

遗传算法中，用编码来表示研究问题的变量，编码构成染色体，按照遗传规律进行选择、交叉、变异。基于罩退工序调度问题特征，染色体编码由三部分组成，第一部分代表类的加工顺序，基因值为类的索引号，第二部分表示加工顺序，基因值表示钢卷索引号，第三部分表示不同的钢卷加工时所选的设备，基因值代表第二部分钢卷选择的退火炉编号。具体示例如下：

类：1，2，3，4

类与钢卷：（1，2，3，4，5，6，7，8，9），（15，16，17，18，19，20，21，22，23，24），（25，26，27，28，29，30，31），（10，11，12，13，14）

设备的编号：1，2，3

则某个体的染色体的构成可以表示为：

第二部分：

第三部分：

3.2 种群初始化

采用随机生成法进行种群的初始化操作，第一部分随机生成类的加工顺序，第二部分根据索引号的大小排列。第三部分首先进行了并行批次数最大批量和最小批量求解，取得各退火炉出现数量后，进行随机化处理，生成第三部分编码。示例如下：

例如：a=4，b=2，N=31，d=3

第二部分：

则 a'=7.5，b'=15

随机生成 c=8，则 c'=3，r=7，r/c'得 m=2，n=1，则（c+m+1）=11，从而由（c+m+1）/d 得e=3，f=2

即1号、2号、3号罩式退火炉出现的次数分别为12次、10次和9次。按照出现次数，随机生成一个顺序列，即得到染色体第三部分的初始编码，结果如下：

第三部分：

3.3 适应度函数

适应度函数用来评价个体在目标函数方向上的优劣程度，适应度值的大小代表个体的结果优劣，适应度函数值越大说明个体越接近最优值，反之则越远离。本文研究以时间最少为目标函数的衡量指标，因此取目标函数的倒数为适应度函数，以保证适应度函数与目标函数的一致性和匹配性。由于工艺条件限制，产品的批次组合必须满足宽度和厚度的要求，因此计算适应度函数时，需首先确定同一设备下加工的钢卷，并将钢卷按照所分批次进行组合，通过钢卷加工顺序和时间，计算出不同批次的完成时间，进而确定不同设备加工完成时间，最终确定订单的完成时间，将时间取倒数，即得到适应度函数的值。

3.4 选择、交叉和变异

遗传算法中的选择是为了将具有较优适应度值的个体选择出来，并作为下一轮计算的基础样本，交叉和变异用于产生新的个体，以更新基础样本。染色体的选择方式很多，本研究分两步实现，首先确定优秀个体占种群个体的比例，而后按照轮盘赌的方式将这些个体选择出来。

交叉是通过不同染色体之间的交叉，以保持种群的多样化，并将优秀的基因遗传到下一代。本文采用江志彬所介绍的方法[9]和PMX方法相结合的方式，并根据实际情况作了相应调整。交叉的实现过程如下：选取个体P1和P2，根据交叉概率选择是否对其进行交叉操作，如果进行交叉则在P1和P2的第一部分编码中随机选取两个位置记为，而后将P1中与C2位置包含的相同的基因码删除，并将C2所包含的基因码置于P1末端，同理对P2进行类似操作。而后，染色体中第二部分，按照新产生的第一部分数据进行相应调整，只调整类的顺序，类中包含的钢卷顺序不做改变。染色体中的第三部分不变。交叉操作过程示例如下：

P1第一部分和第二部分染色体基因码分别如下：

P2的第一部分和第二部分染色体基因码分别如下：

P1与P2交叉操作示意图如下：

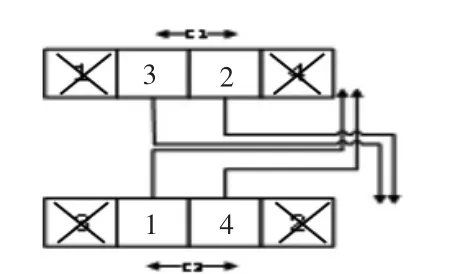
得到结果：

染色体第二部分对应第一部分进行相应调整，得到结果为：

染色体变异是按照一定的变异率，为个体进行变异操作，以增加种群的多样性，避免算法过快收敛而趋近局域最优解。本研究通过初始化染色体第三部分进行变异操作。

4 算例及结果

为验证所构建算法的有效性，本文对算法进行了实例运算。算法数据取自于国内某薄板厂真实数据，提取算法中的变量及参数，主要包括：罩退工序订单交货期、罩退工序类的划分、设备台数、设备高度、钢卷的宽度厚度、钢卷所需的加工时间。具体见下表1、表2所示。

表1 算例订单数据（节选）

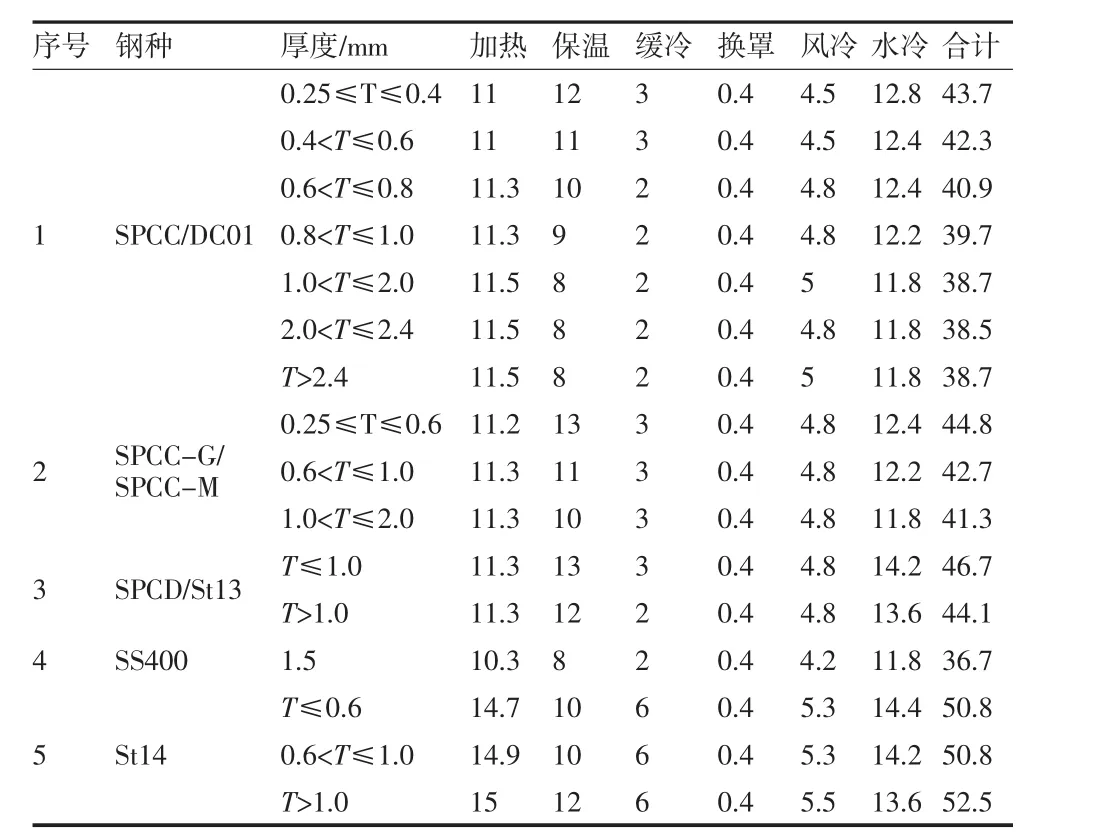
表2 不同型号钢卷罩退工序加工时间（小时）

在代入算法计算之前，对订单按照交货期的紧迫程度确定了订单权重，距离交货期越近，则订单权重越大。选取订单中前147个类代入算法进行运算，结果显示，遗传代数接近150代时，结果趋于收敛。将遗传算法最大代数设为500，结果基本收敛于2.76×104，如图2所示。调度方案运算结果共计2424列，文中不再展示。

图2 示例运算结果

为了验证订单规模对运算结果的影响，使用遗传算法进行了不同订单规模罩退工序时间的计算，统计结果如表3所示。

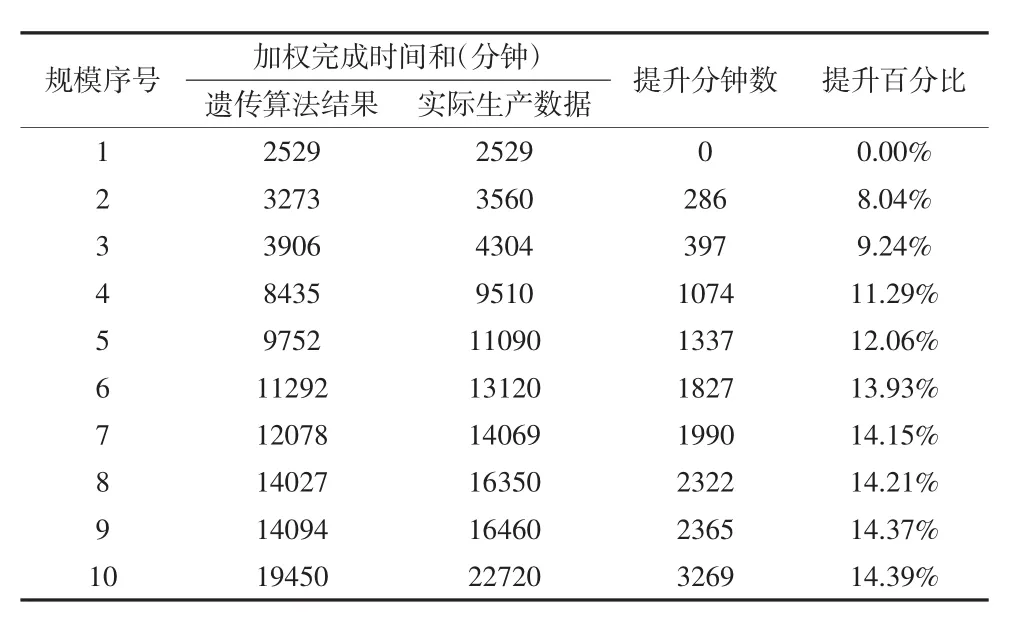
表3 不同订单规模算法计算结果与实际生产数据比较

运算结果显示，不同订单规模下，遗传算法运算结果均优于实际生产过程中的订单完成时间。其中，订单规模为1时，生产调度问题较为简单，由人工即可计算得出较优结果，算法计算结果与实际组织生产时差异不大，事实上，这是一种临界情况，在生产过程中极少出现。当订单规模大于等于2时，由于同一订单本身包含不同的产品，因此具备一定的计算难度，在多种因素制约下，已经很难由人工计算取得最有解。计算结果同时显示，随着订单规模的增加，优化效果越来越明显，但当达到一定规模后，优化效果趋于稳定。

5 结论

本文针对钢铁薄板生产中罩退工序制约因素多，资源调配困难的问题，基于企业生产实际，综合考虑多种制约因素，构建了以最小化订单完成时间为目标的数学模型，并通过遗传算法进行求解。结果显示，遗传算法求解算例验证了算法的有效性，罩退工序订单完成总时间明显优于现行实际加工时间，且随着订单规模的增加，算法取得的优化效应逐渐增加，但订单规模达到一定程度后，优化效果趋于稳定。一方面，当前产品生产调度问题存在改进空间，另一方面，时间效率的上限为100%，因此算法的优化效益存在上限。本研究为薄板生产中罩退这一瓶颈工序调度问题提供了可参考的思路，由于薄板生产罩退工序具有相似性，因此模型和算法适当调整后可用于其他企业或者行业的调度问题优化。按照研究思路，所用模型和方法可推广延伸至其他工序，累计效益将更加显著。研究方法和结论可为企业生产计划和调度提供借鉴和帮助。