双层差值扩展可逆数字水印算法

苏文桂 沈玉龙 王 祥

1(西安电子科技大学计算机科学与技术学院 西安 710071)2(广西制造系统与先进制造技术重点实验室(广西大学机械工程学院) 南宁 530004)3(西安电子科技大学通信工程学院 西安 710071)

在过去的几年里，数字媒体的使用大幅增加了在线数据攻击和版权侵犯等问题.数字水印技术是一种新的信息隐藏技术，将秘密信息隐藏到数字媒体载体中来实现数字版权保护和内容认证[1].而原始媒体由于水印的嵌入，会遭受不可擦除的失真，在一些高保真的应用场合，比如法律、医学图像、军事图像、遥感等，即使是非常轻微的失真也是不能容忍的.因此，可逆数字水印应运而生.可逆数字水印也称为无损水印，在水印嵌入后能从媒体中成功地提取嵌入的秘密信息并且无损恢复原始媒体.在目前的研究中，基于图像的可逆数字水印是可逆数字水印技术研究的热点.作为信息隐藏技术的一个重要分支，可逆水印侧重于数据隐藏行为的不可感知性及可恢复性.现有的可逆水印在本质上是脆弱水印，对于可能遭受的攻击没有鲁棒性，当宿主图像遭到轻微改变或攻击时都会对水印造成影响，主要用于数字图像的真伪鉴别和完整性保护.可逆数字水印的2个重要特性是不可感知性和嵌入容量.简单地说，不可感知性是嵌入水印后的图像与宿主图像相似度的度量，嵌入水印后的图像质量不能出现明显的下降；而嵌入容量是宿主图像能携带信息量的度量，指能够嵌入到宿主图像中并能提取的最大信息量.不可感知性和嵌入容量是相互制约的2个指标，当嵌入容量高时图像会出现明显的视觉失真，而当嵌入容量低时图像的失真较小.一个可逆水印算法应能在保持一定失真的情况下,具有尽可能大的嵌入容量.我们通常采用嵌入失真率和嵌入容量这2个指标来评价一个可逆水印算法的性能.常见的基于图像可逆数字水印算法可以归纳为三大类：

1) 基于无损压缩的可逆数字水印算法.这类算法通过无损压缩原始载体图像的一部分为水印创造嵌入空间[2]，但是这种算法的水印嵌入容量有限.早期的基于无损压缩的可逆信息隐藏方法由于水印嵌入容量有限并且有可能导致嵌入后图像质量的明显下降，主要应用于图像完整性认证和版权认证.

2) 直方图平移(histogram shifting， HS)可逆数字水印算法.这类算法把灰度值在图像直方图峰值和零值之间的像素平移1个单位来嵌入水印，可以获得较高品质的嵌入图像，但是最大嵌入容量受限于直方图峰值点像素数量.为提高嵌入容量，近年来很多学者在直方图平移技术基础上进行了进一步的改进[3-4].Chen等人[3]从图像对比度增强、视觉失真减少和嵌入容量增加3个方面对直方图平移算法进行了改进.通过直方图的分布特性自适应调整直方图平移过程来增强图像对比度，将直方图预平移中像素修改范围减少一半来减少图像失真，并通过像素值排序技术来提高嵌入容量.文献[4]利用矩形预测误差分布的特点，首先将直方图峰值向右移动用于嵌入水印信息，然后再将峰值向左移动以留下更多的空间用于更多的数据嵌入，这可以减少由于直方图右移动造成的失真，实验证明该算法能获得较大的嵌入容量和较小的失真.

3) 基于Tian[5]提出的差值扩展(difference expansion, DE)的可逆数字水印算法.DE算法把图像相邻像素对的差值进行扩展来嵌入1b水印，它的缺点之一是嵌入水印信息后图像的质量普遍较差.近年来大量高效的预测算法提出以提高DE算法的性能，在整数小波变换[6-7]、预测误差扩展(prediction-error expansion, PEE)[8-9]、像素值排序(pixel-value-ordering, PVO)[9-11]等方面得到广泛的研究和发展.Wang 等人在文献[6]中提出了一种基于有效整数变换的可逆水印算法，将DE技术扩展到任意长度的像素块，同时优先选择引入较少失真的可嵌入块来控制失真，取得了很好的嵌入性能.Weng等人[7]提出了一种基于整数Haar小波变换的新DE算法，利用块的不变平均值评估局部复杂度来选择嵌入块的大小，运用差值扩展(或直方图平移)进行嵌入.PEE算法通过引入直方图平移算法高效地压缩位置图，使用预测误差来代替差值扩展算法中的相邻像素差值来获得更尖锐的直方图.Ou等人[8]提出一种新的算法集成了成对的PEE和一种自适应的2D映射选择机制，在嵌入时为图像中的粗糙像素对和平滑像素对选择不同的嵌入机制，进一步优化了嵌入性能.Yu等人[9]提出了一种基于多维PEE的可逆水印算法，并通过摒弃可能产生高失真的嵌入映射来减小嵌入失真.由于只需考虑嵌入失真阈值的最简单情况，该算法更适合纹理简单和平滑的图像.像素值排序预测算法是近年来高保真可逆信息隐藏方法，通过预测和修改像素块的最大值和最小值嵌入数据，并且通过保存像素值排列次序保证了可逆性.文献[10]提出了一种自适应预测模型和最佳箱选择策略的PVO可逆数据隐藏方法，利用每个待嵌入像素周围的邻域来测量局部复杂度，提高了预测性能.He等人[11]提出了n阈值和n级分块的多级分块策略，根据分块类型选择不同的嵌入方案.Ou等人[12]将多重直方图修改引入到现有的PVO算法中，对PVO算法进行了改进.

Tian[5]的DE算法中单遍嵌入最大嵌入率为0.5 bpp，为提高嵌入率需要进行多遍嵌入.第1遍DE嵌入后图像像素间的相关性明显降低.若直接采用同样的像素对分组方式对图像进行第2遍嵌入，嵌入后图像质量将会显著降低.为达到嵌入容量和低失真之间的平衡，本文在Tian提出的DE算法的基础上，提出一种新的可逆水印嵌入算法.在嵌入方法上采用正交双层嵌入方案，第1层嵌入采用传统的Tian[5]提出的DE算法对像素对进行分组嵌入，通过分析嵌入失真与嵌入位置的关系，第2层嵌入使用正交方向对像素对进行分组嵌入，在提高水印嵌入容量的同时减少图像的失真.在嵌入单元的选择方面，引入像素对均值局部方差作为图像平滑度的度量，优先选择平滑的像素对嵌入数据，使失真得到较好的控制.

1 Tian的差值扩展可逆数字水印算法

Tian[5]提出的差值扩展可逆水印算法中，对于1幅8 b灰度图像中的1个像素对(x,y)，x，y∈Z,0≤x,y≤255,定义该像素对整数平均值l和差值h分别为

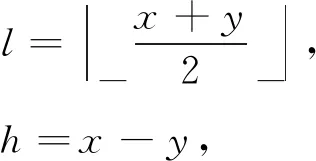
(1)

式(1)的逆变换为

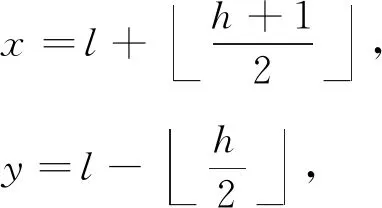
(2)

对差值h进行扩展将1 b的信息b(b∈{0,1})嵌入，扩展后的差值h′为

h′=2h+b.

(3)

定义可扩展和可变的差值为：

1) 若|2h+b|≤min(2(255-l),2l+1)，则差值为可扩展的；

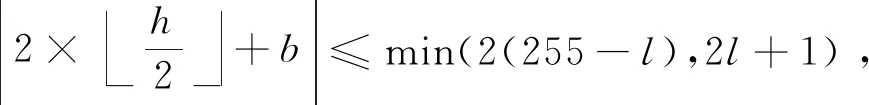
可扩展差值也属于可改变差值.对于可变差值，修改它们的最低有效位(least significant bit， LSB)，修改后的差值仍然是可改变的.

将差值h分为4类，分别放入EZ，EN，CN，NC这4个不相交的集合中.其中EZ包含所有可扩展的差值h=0和h=-1.EN包含所有可扩展的差值h∉EZ.设置阈值T,通过T进一步将EN分为EN1(h≤T),EN2(h>T).CN包含所有可改变的差值h∉(EZ∪EN).NC包含所有不可改变的差值.待嵌入的比特流嵌入差值中：

(4)

嵌入后像素对(x′,y′)可计算为

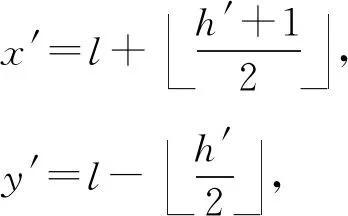
(5)

水印嵌入完成.

提取流程为嵌入流程的逆过程，在此不再详述.

2 本文提出的算法

2.1 嵌入像素对选择

经典的DE算法在水印嵌入后对图像的峰值信噪比(peak signal-to-noise ratio，PSNR)影响较大.DE算法通过扩展或者改变像素对差值h来完成嵌入，选择较小的差值h进行嵌入将会减小由于水印嵌入导致图像的失真.为了保证可逆性，根据图像不同区域具备不同的统计特性，我们利用图像局部区域像素对平均值l的局部方差v作为平滑度的预测器.由于在嵌入前后，像素对的平均值l保持不变，因此由平均值l计算出的局部方差v保持不变.在提取端，依然可以利用均值局部方差区分出该像素对是否为平滑块.同时若局部方差v值较小，意味着图像纹理较平滑，像素对差值h较小.因此，嵌入时尽可能选择处在平滑图像区域的像素对进行嵌入，可以提高嵌入水印后的图像质量.

假设原始图像I是1幅大小为n1×n2(n1=n2=512)的灰度图像I={(i,j),1≤i≤n1,1≤j≤n2}，其中i,j代表图像I的第i行、第j列.根据DE算法，在嵌入水印时，首先将I中的像素按照水平或者垂直的方向分为像素对.以水平方向分组的像素对(i,2j),(i,2j+1)为例，用于计算局部方差的像素对平均值l(i,j)及其周围的8个像素对平均值如图1所示.均值l(i,j)处的局部方差v(i,j)计算为

(6)

根据嵌入容量引入阈值T，T>0.当v(i,j)≤T时，我们认为该像素对处在平滑区域，当v(i,j)>T时，像素对处在不平滑区域.应用算法进行嵌入时，对平滑区域的像素对计算差值并进行分类，平滑区域内的所有可扩展差值全部用于嵌入，由于平滑区域内差值h较小，优先选择用于嵌入可以减少失真，提高图片的PSNR.

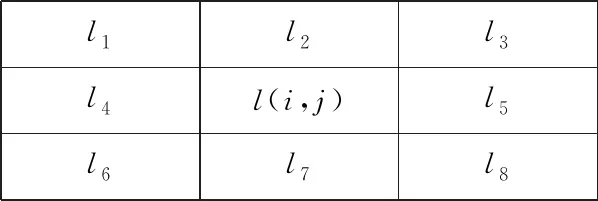
l1l2l3l4l(i,j)l5l6l7l8

Fig. 1 Mean region of pixel pair
图1 像素对均值区域

2.2 双层嵌入方案

为了进一步提高嵌入容量，本文提出了基于DE算法的双层嵌入方案.双层嵌入指的是在原始图像上完成1次全图的嵌入，再在得到的水印图片上进行第2次嵌入.

1) 第1层嵌入.在第1层嵌入时，我们按照传统的Tian[5]提出的DE算法，将原始图像上的像素分为两两互不重叠的像素对，完成像素对分组后，按照DE算法进行第1层的水印嵌入.

2) 第2次嵌入.与第1次嵌入相比，第2次嵌入时我们调整像素对分组方式，使用与第1次分组方式正交的方向对像素两两分组.也就是说，如果第1次嵌入时，我们使用水平方向分组的方法，那么第2次嵌入时，就采用垂直方向两两分组的方法.

3) 嵌入失真讨论.本文采用双层嵌入的方式，在第2层嵌入时采用与第1次不同的像素分组方式，这样的调整将会减小第2次嵌入带来的失真，下面我们对这一说法做出证明.

x1y1x2y2

Fig. 2 Embedded pixel pair
图2 嵌入像素对

第1层嵌入.以第1次嵌入使用水平分组为例，像素对分为(

x

1

,

y

1

)(

x

2

,

y

2

)共2组，对于像素对(

x

1

,

y

1

)，均值和差值分别用

l

11

，

h

11

表示，第1层嵌入完成后像素对为

根据式(1)(3)(5)，得到:

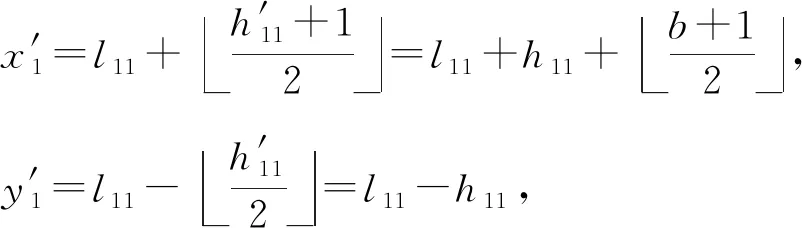
(7)

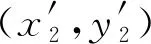
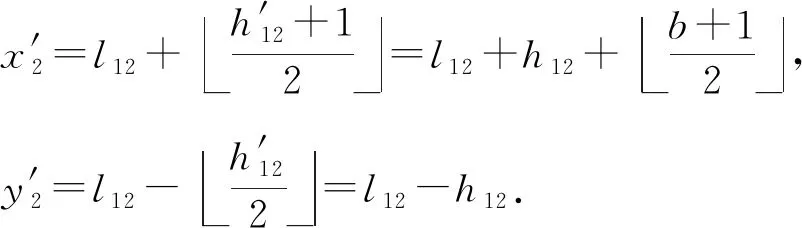
(8)

第2层嵌入.我们通过计算第2层嵌入时调整分组方法与不调整分组方法这2种情况引起的嵌入误差来说明采用调整分组方式能减少嵌入误差.

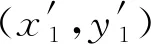
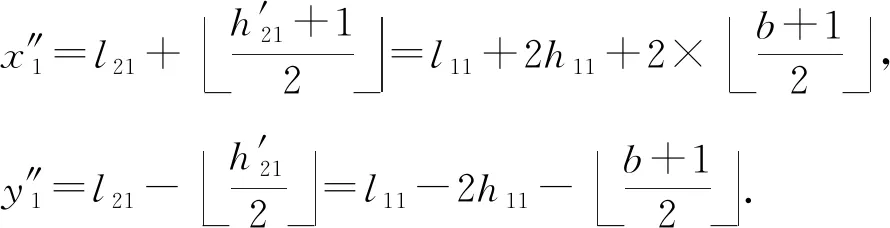
(9)

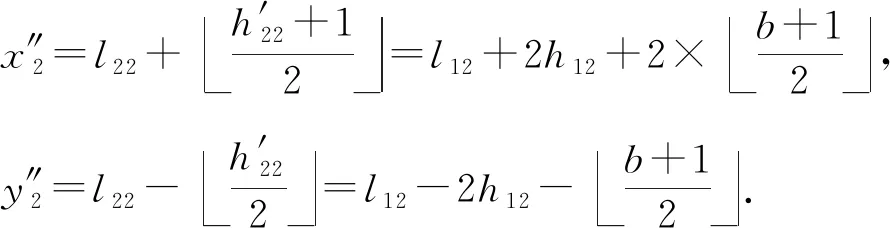
(10)

以像素对(x1,y1)为例，第2次嵌入完成后带来的失真为

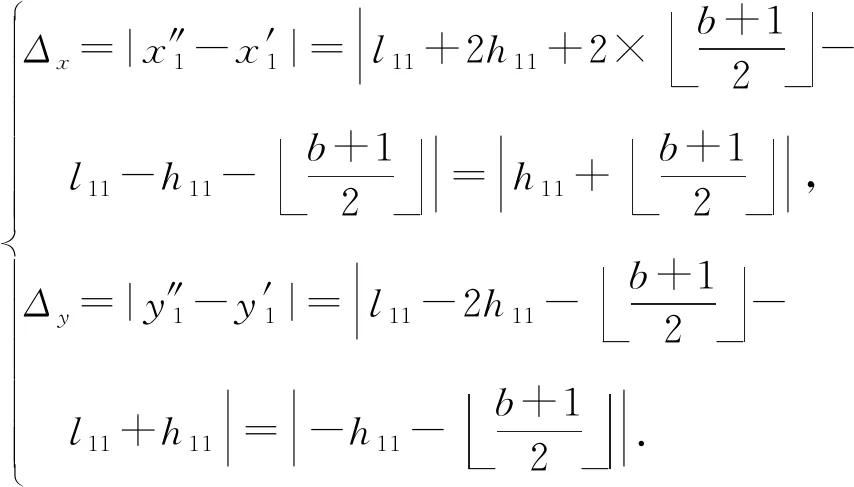
(11)

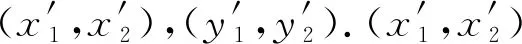
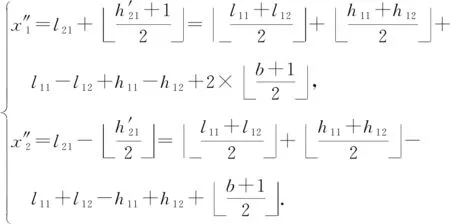
(12)

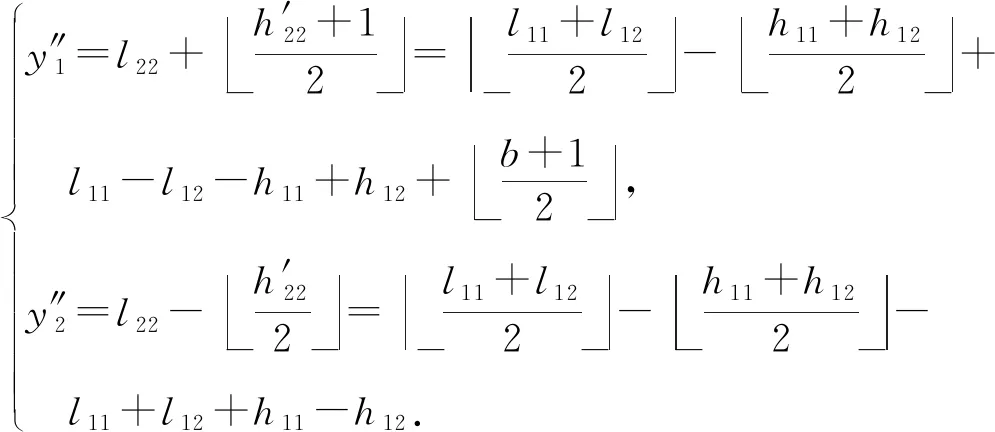
(13)

与第1次嵌入完成后的像素值相比，第2次嵌入带来的失真为

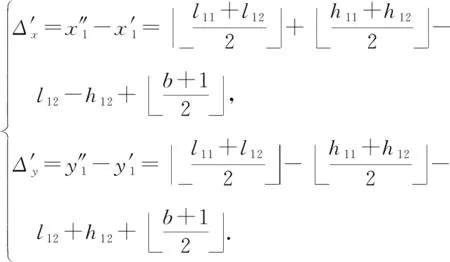
(14)

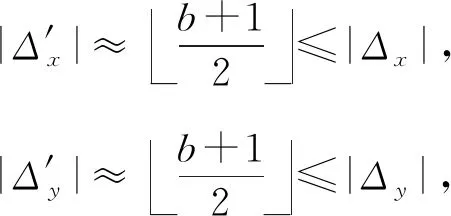
(15)

由式(15)可见，在第2次嵌入时，改变像素的分组方式，将会减少一定的失真.

2.3 嵌入流程

以像素对先按水平方向分组为例，对于原始图像I和阈值T>0，嵌入过程可以分为5步：

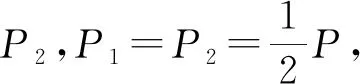
Step2. 根据式(7)，由平均值矩阵计算每组像素对的局部方差vH(i,j).选择阈值T，将像素对分为平滑(vH≤T)和不平滑(vH>T)两类.其中，平滑的像素对用来嵌入水印，不平滑的像素对保持不变.

Step3.计算平滑的像素对的差值hH{hH1,hH2,…,hHn}，将hH分为ET,CT,NCT三类.

ET：包含所有可扩展差值hH，且vH≤T；

CT：包含所有可改变差值hH，hH∉ET；

NCT：包含所有不可改变差值.

创建位置图LM：若h∈ET，LM=1；若h∈(CT∪NCT)，LM=0.将LM用JBIG2无损压缩，压缩后的水印序列记作LH.

Step4. 记录所有CT差值集合的LSB,并将其组成水印序列CH.对于双层嵌入，需要在水印序列LH之前嵌入48 b头信息F,包括16 b配对模式、24 b嵌入容量长度、8 b阈值T.嵌入水印序列BH=F∪LH∪CH∪P1，得到水印图像I′.

Step5. 第2层需嵌入水印序列P2.将图像I′按照垂直方向，把相邻的像素两两分为互不重叠的像素对，计算每组像素对的平均值，生成像素对的平均值矩阵lV.重复Step2开始的嵌入过程，得到最终的水印图像I″.

2.4 提取流程

提取时，分为2层提取.首先提取第2层嵌入的水印并恢复出图像I′；然后，在图像I′上提取第1层嵌入的水印并恢复出图像I.

Step1. 提取第2层嵌入的水印.将最终的水印图像I″的像素按照垂直方向分为两两1组的互不重叠的像素对.计算像素对的平均值矩阵lV.

Step2. 由平均值矩阵lV计算每组像素对的局部方差vV(i,j)，选择平滑的像素对，计算差值hV{hV1,hV2,…,hVn}，把像素对按照差值hV分为2类,其中CHV包含所有可改变的差分；NCV包括所有不可改变的差分.

Step3. 选择所有在CHV中的差值的LSB组成比特流BV，提取前48 b头文件后解码位置图，根据位置图来还原原始差值，并根据式(2)恢复图像I′.

Step4. 在图像I′上提取第1层嵌入的水印.对I′的像素按照水平方向分为两两1组的互不重叠的像素对，计算像素对的平均值矩阵lH.按照Step2同样的方法提取水印信息，并恢复出图像I.

3 实验结果分析

我们提出的算法与Tian[5]算法和近年来提出Wang[6]算法进行实验比较，从图像的峰值信噪比和嵌入容量进行对比来评价本文算法的嵌入性能.Tian[5]算法是基于差值扩展的可逆水印经典算法.Wang[6]算法从整数变换的角度改进了Tian[5]算法，通过构造广义整数变换和依赖于有效载荷的位置图将DE技术扩展到任意长度的像素块，使用像素块的平均值来预测块内的像素，获得了较高的嵌入容量和低失真.

用于实验的6幅512×512标准灰度图像Lena，Airplane,Baboon，Barbara，Goldhill，Boat均下载自USC-SIPI图像数据库.实验结果如图3所示.在标准的灰度图像Lena，Airplane,Baboon，Barbara，Goldhill中，本文提出的算法相比于Tian[5]算法在PSNR和最大嵌入率上均有明显的提升，在低嵌入率时本文的算法取得了较高的PSNR,同时Tian[5]算法最大嵌入率为0.5 bpp，本文算法最大嵌入率可达到1 bpp.在图像Boat中，当嵌入率小于0.3 bpp时，Tian[5]算法略优于本文提出的法，嵌入率大于0.3 bpp时，本文算法优于Tian[5]算法.说明本文提出的算法通过选择平滑块并使用正交双层嵌入，在提高嵌入容量的同时保持了较高的图片质量.

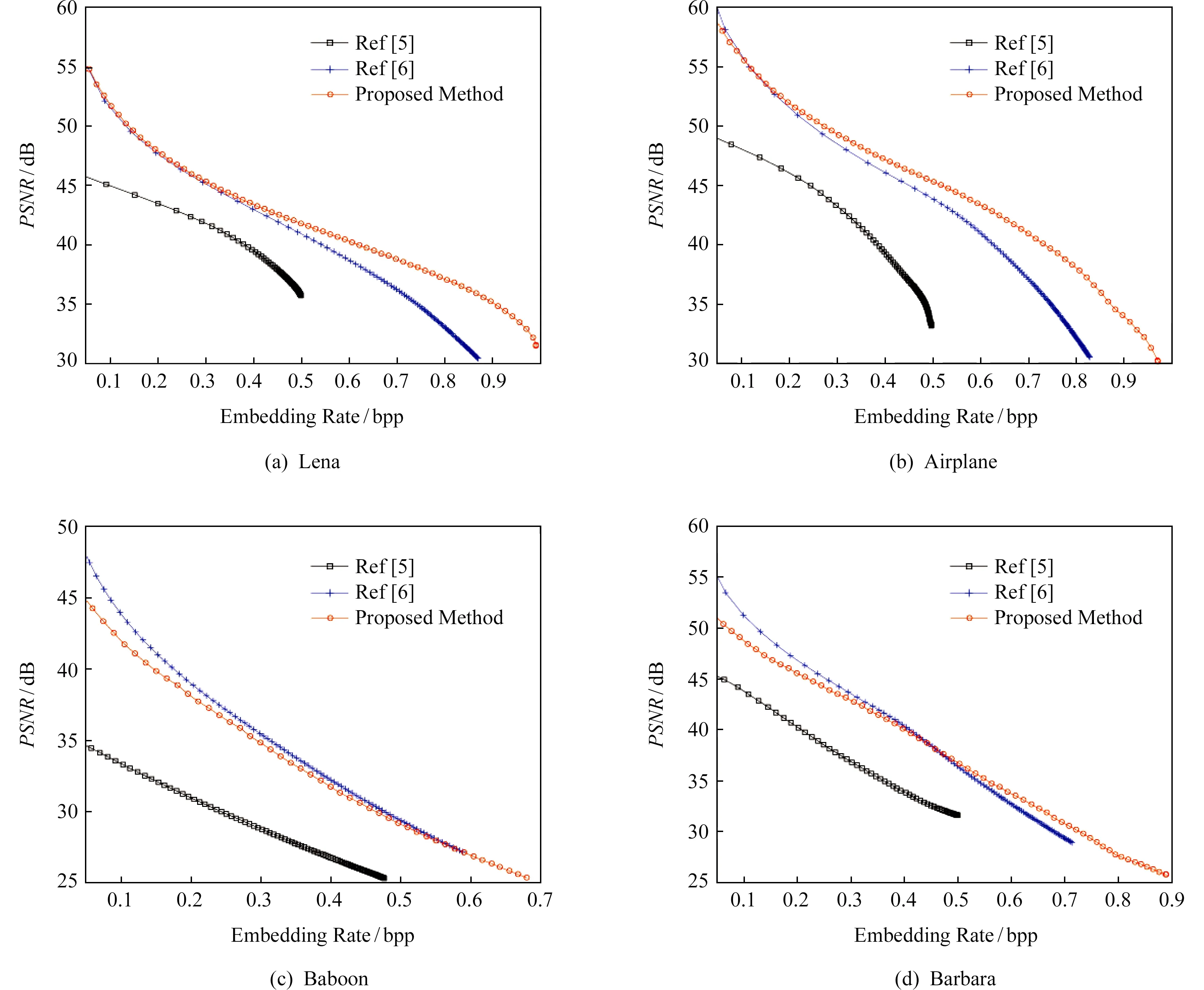
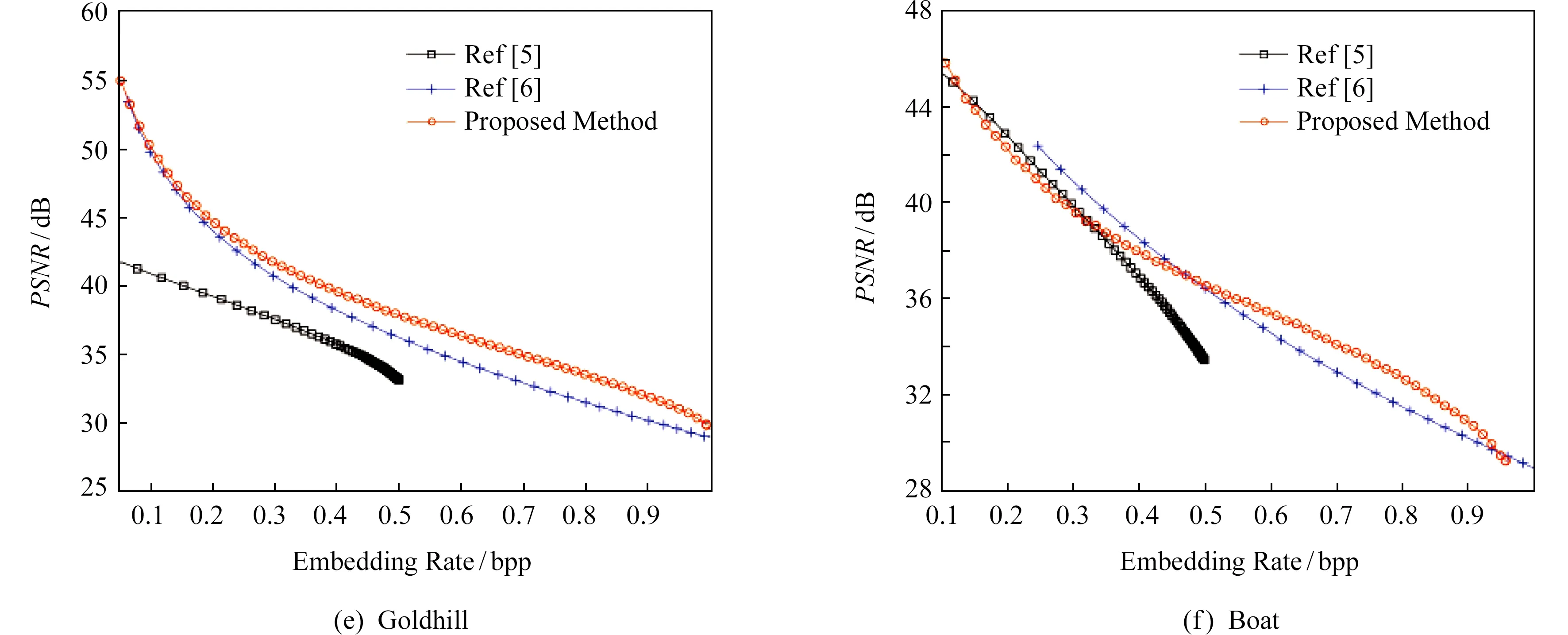
Fig. 3 Embedding performance comparison on the proposed scheme and other schemes图3 本文算法和其他算法的嵌入性能比较

在图像Lena，Airplane，Goldhill中，在低嵌入率时本文的算法的嵌入性能与Wang[6]算法接近，随着嵌入率的增大，本文提出的算法提供了较好的嵌入性能.图像Baboon中，Wang[6]算法的嵌入性能略优与本文提出的算法.对于纹理复杂的图像Baboon，Wang[6]算法通过优先选择引入较少失真的块来嵌入数据，因此图像失真得到较好的控制.在图像Babara，Boat中，当嵌入率低于0.45 bpp时，Wang[6]算法相对于本文的算法获得较高的PSNR;当嵌入率高于0.45 bpp时本文的算法获得较高的PSNR值.在图像Lena，Airplane，Baboon，Barbara中，本文算法获得比Wang[6]算法更高的最大嵌入率.

为了进一步验证本文提出方案的优越性，在常用的6幅512×512标准灰度图像Elaine，Pepper，Fishboat，Lake，House，Tiffany上利用计算本文提出的算法计算在嵌入率为0.4 bpp时图像平均PSNR值，并与Wang[6]算法和Tian[5]算法在0.4 bpp嵌入率下获得的平均PSNR进行对比，结果如表1所示:

Table 1 Comparison of Average PSNR Between the ProposedScheme and Other Schemes for an Embedding Rate of 0.4 bpp

表1 0.4 bpp嵌入率下本文算法与其他算法平均PSNR对比

SchemeAverage PSNR∕dBRef [5]35.5Ref [6]39.6Proposed Method40.2

从表1比较结果得出，本文提出的算法在0.4 bpp嵌入率下，相对于Tian[5]算法平均PSNR提升了4.7 dB，相对于Wang[6]算法提升了0.6 dB，本文提出的算法获得了较好的图像质量.

4 结 论

本文提出了一种新的双层差值扩展可逆水印算法，新算法根据像素对均值局部方差大小优先选择差值较小的像素对进行水印嵌入，保证了可逆性同时减少了图像失真.使用双层嵌入，增大了嵌入容量，并在第2次嵌入时，通过改变像素对分组方式，减少了嵌入失真.实验结果表明:提出的算法能在提高嵌入容量的同时保持较好的图像可视性，提高了嵌入性能.