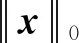基于自适应局部搜索的进化多目标稀疏重构方法
2019-07-15刘昊霖池金龙邓清勇裴廷睿
刘昊霖 池金龙 邓清勇 彭 鑫 裴廷睿
1(湘潭大学信息工程学院 湖南湘潭 411105)2(物联网与信息安全湖南省重点实验室(湘潭大学) 湖南湘潭 411105)3(湖南理工学院信息科学与工程学院 湖南岳阳 414000)
压缩感知(compressed sensing, CS)把信号采样和压缩相结合,突破了传统的奈奎斯特采样定律.压缩感知理论主要分为3个分支:稀疏表示、观测矩阵的设计和信号重构[1],其中信号重构在各领域起着重要作用.信号重构的本质是通过M维观测信号(M≪N)恢复一个长度为N的信号.考虑稀疏信号向量x∈RN,根据压缩感知理论可知,在理想情况下可以恢复出原始信号x:
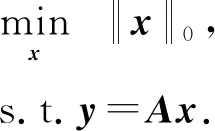
(1)
而当观测过程中存在噪声n时,观测向量为y=Ax+n(n∈Rm).众所周知,直接求解l0范数是一个NP困难问题,可以使用一些方法来求解[2].贪婪算法:包括正交匹配追踪(orthogonal matching pursuit, OMP)[3]和子空间追踪(subspace pursuit, SP)[4]、迂回式匹配追踪(detouring matching pursuit, DMP)[5]等;松弛法:包括基追踪(basis pur-suit, BP)[6]、基追踪去噪(basis pursuit denoising, BPDN)[7]、匹配追踪(matching pursuit, MP)[8];迭代阈值算法(iterative soft-thresholding algorithm, IST)[9]等.


1) 由于2种局部搜索方法产生2个解,保证解的多样性,提高了全局解的可信度;
2) 通过比较2个解的优劣性,保证下一个解总是由前最优解产生,提高解的精确度;
3) 由于在进化前期对解进行了批量搜索,获得了足够多高质量的解,在后期只需选择一个优胜的局部搜索方法,既保证了后期解是在最优方法下产生的,又减少了计算成本.
1 相关工作
多目标进化算法主要有非支配排序遗传算法(non-dominated sorting genetic algorithm, NSGA-II)[14]和基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEAD)[15]两大类.NSGA-Ⅱ适合估计连续的帕雷托前沿(Pareto front, PF),而当PF不连续或非凸时很难找到PF的膝盖区域(knee region, KR).而且,由于该算法采用拥挤距离来控制种群的多样性,在寻找KR时会被有些次优解干扰导致定位不准确,最优目标向量在PF上难以呈均匀分布.MOEAD算法将目标函数分解成多个子目标函数,加入规范化技术来处理不同比例的目标函数,从而将偏好整合在PF的局部区域,且可以进化出1组在PF上均匀分布的解.
已有文献将多目标进化算法应用在稀疏重构问题上,其中文献[16]提出了多组优化算法来提高在有噪声环境中的重构精度;文献[17]提出软阈值进化多目标算法(soft-thresholding evolutionary multi-objective, StEMO),通过单次运行产生的1组解来同时优化测量误差和信号稀疏度,最后在PF[18]的KR上获得最优解;文献[19]提出了多目标稀疏模型并且将其用于神经网络;文献[20]提出了多目标自步学习模型(multi-objective self-paced learning, MOSPL)用于解决在初始化过程中参数设置的敏感问题;另外,多目标进化算法也在图像处理领域得到了应用[21-22],文献[23]提出了多目标稀疏解混模型(multi-objective sparse unmixing, MOSU)用于高光谱图像解混.
2 多目标问题及求解方法
2.1 基本定义
多目标问题可以描述为
minF(x)=(f1(x),f2(x),…,fm(x))T
(2)
s.t.x∈Ω,
其中,Ω⊆Rm表示决策空间,x=(x1,x2,…,xn)T为n维决策向量,Ω={x∈Rm|hj(x)≤0,j=1,2,…,m},hj是连续函数,F:Ω→Rm是由m个目标函数组成,Rm是目标函数空间[24].对于解的支配关系有定义,当且仅当:
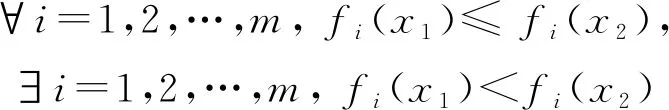
(3)
成立时,称x1支配x2,表示为x1x2.若在解空间中不存在x比x*要好,则称x*为帕累托最优解,表示为x*x.最优解的目标函数值所组成的集合称为SPF[25],表示为
SPF={(f1(x*),f2(x*),…,fm(x*))T|x*∈X*}.
(4)
2.2 切比雪夫分解模型
基于分解的多目标进化方法通常是将前沿面的逼近问题转化为若干个标量优化问题,一般有3种方分解法,分别是加权法[26]、边界交集法[27]和切比雪夫法[28].加权法针对凸问题具有更好效果,而边界交集法必须处理等式约束问题,需要设置惩罚因子,但是惩罚因子的值会影响算法性能.本文采用切比雪夫分解方法,通过调整权重向量来获得不同的帕累托最优解,其模型可表示为
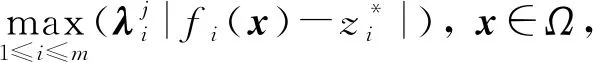
(5)
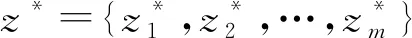
3 方法论
3.1 多目标稀疏重构模型
稀疏重构问题可以近似等价为求解式(1)中x的非零项的位置,在传统方法求解中,通常利用权重参数将测量误差项和稀疏项聚合成一个函数,但是权重参数的值会影响求解精度.为了解决权重参数对重构精度影响的问题,本文采用多目标进化算法,将测量误差和信号稀疏度作为2个目标函数:
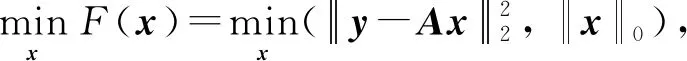
(6)
3.2 ALSEMO算法描述
算法1.ALSEMO算法.
输出:解集{x1,x2,…,xN}对应的目标函数组成的集合SEF、目标函数值向量F=(F1,F2,…,FN).
步骤1. 初始化:
步骤1.1. 设SEF=∅,k=0.
步骤1.2. 计算出任意2个权重向量之间的欧氏距离,然后获得任意一个权重向量与之最近的T个权重向量并将其作为邻居.对任意的i=1,2,…,N,假设B(i)=(i1,i2,…,iT),λi1,λi2,…,λiT是距离λi最近的T个权重向量.
步骤1.3. 初始化{x1,x2,…,xN}为第1代种群,其目标函数向量Fi=F(xi).
步骤1.4. 初始化参考点集合z*.
步骤2. 循环与更新:
Fori=1,2,…,Ndo
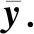
步骤2.2. 执行局部搜索方法:分别将2种局部
步骤2.4. 执行竞争策略选出非支配解:通过比较ya,yb的目标函数值大小,选择出目标函数值小的解作为非支配解ns.
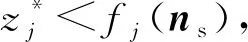
步骤2.6. 更新相邻的解和SEF:对任意的j∈B(i),如果gte(ns|λj,z*)≤gte(xj|λj,z*),则xj=ns,Fj=F(ns),移除在SEF中所有被F(ns)支配的向量,如果在SEF中没有向量可以支配F(ns),那么就把F(ns)添加到SEF中.
步骤3. 重复步骤2直到k=Maxt;
步骤4. 获得PF解集{x1,x2,…,xN};
步骤5. 在PF上用基于角度的方法[18]找到KR并且找出一个最优解.
算法1中初始化种群{x1,x2,…,xN}是由3个步骤完成的:1)随机产生一个从1~N的整数排列作为x的稀疏支撑集S;2)所有的x都设置为N×1的矩阵;3)产生一个1×K的随机数矩阵,其元素值在0~1之间,然后将这些元素值分别赋值给支撑集S的1~K个索引,K在本文中表示信号稀疏度.
3.3 差分进化操作
y-r={xi1r+θ×(xi2r-xi3r), 概率为ω,xi1r, 概率1-ω,
(7)
其中,θ和ω是2个差分进化控制参数.步骤2.2中局部搜索方法(见3.6节)用来提高解的质量.
3.4 修剪策略和高斯变异
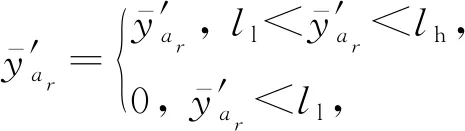
(8)
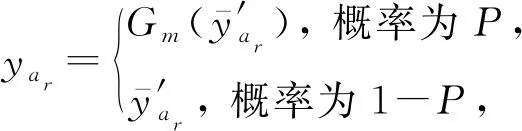
(9)
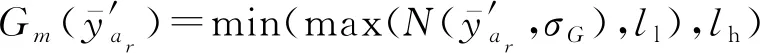
3.5 竞争策略
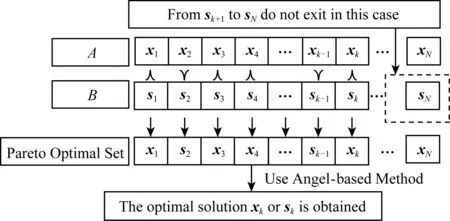
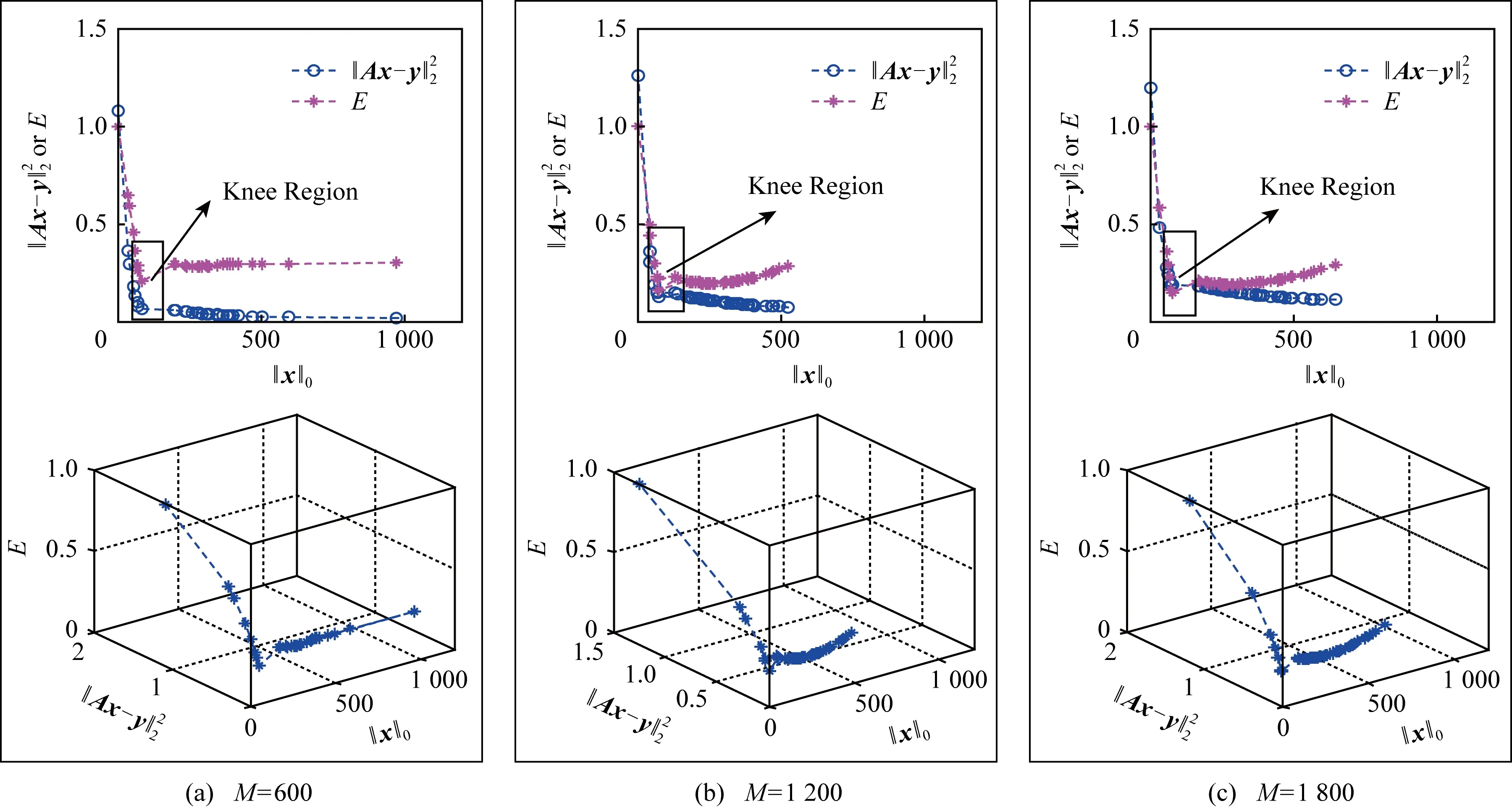
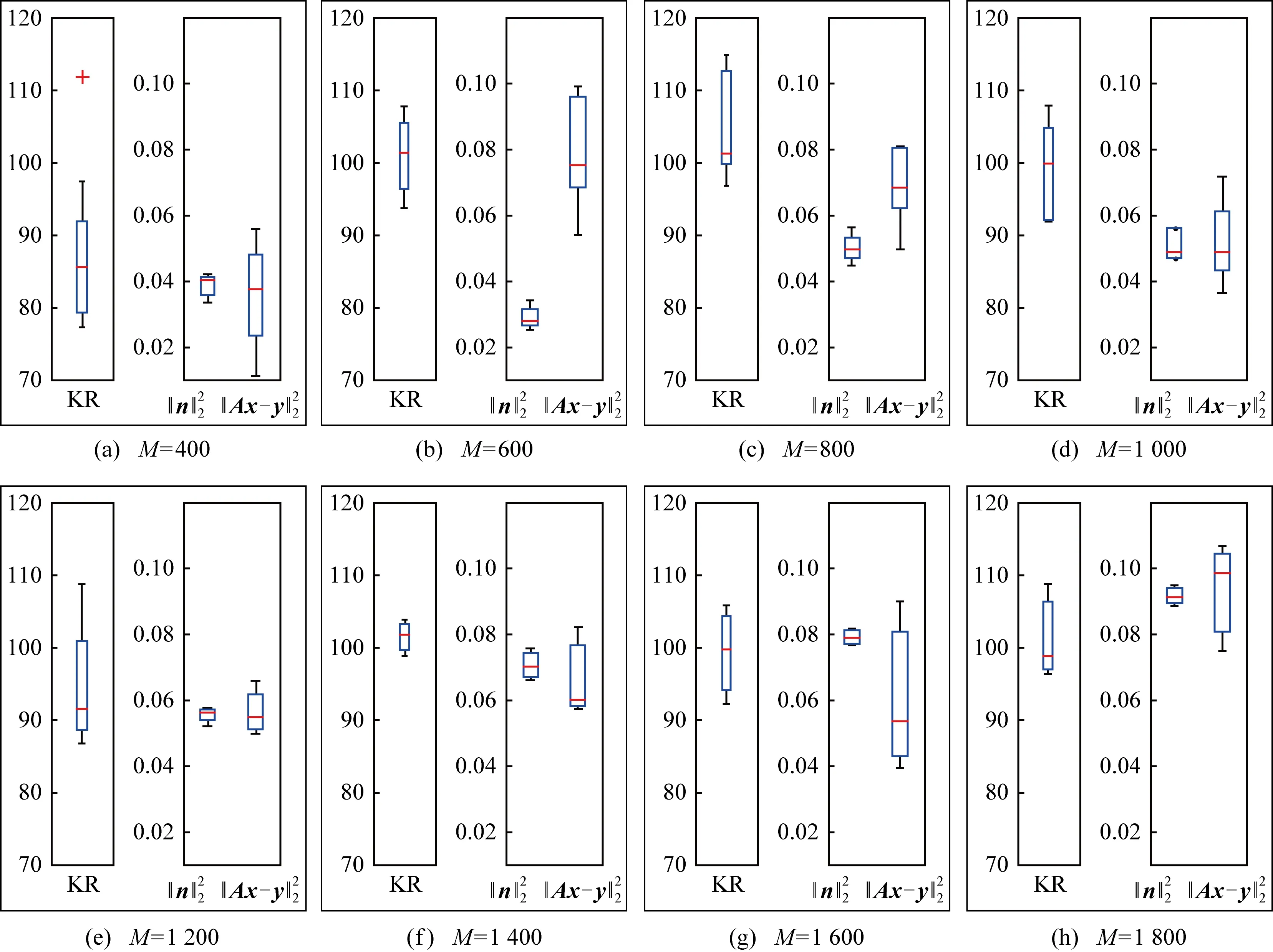
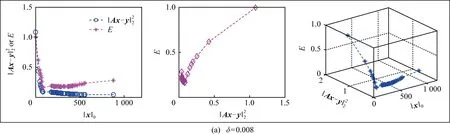
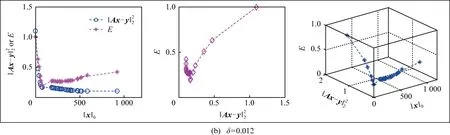
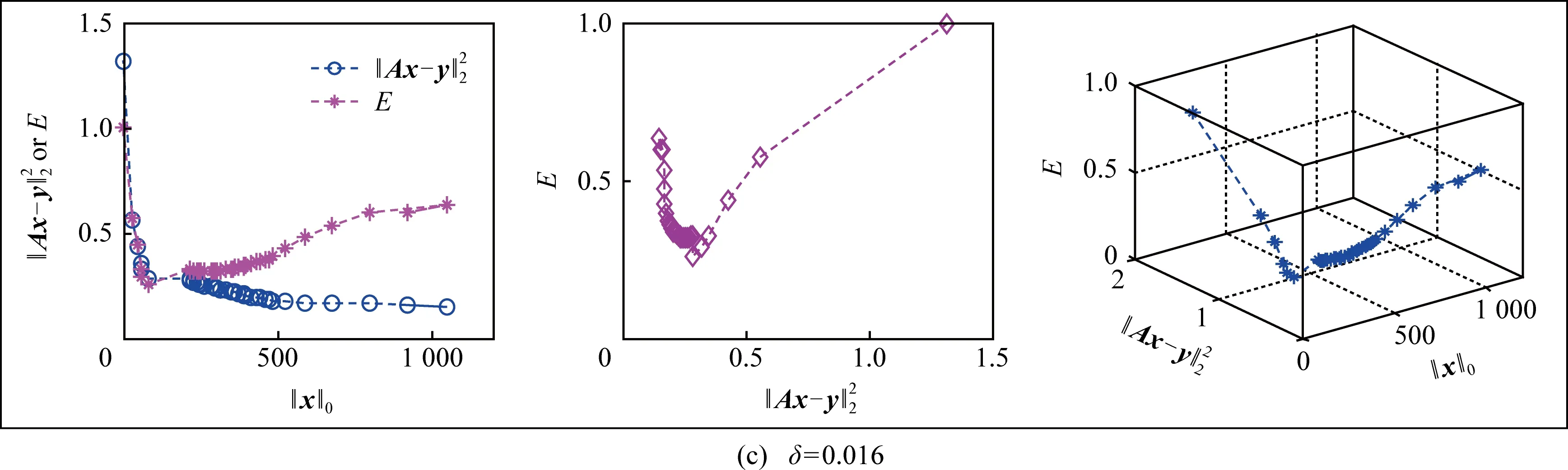
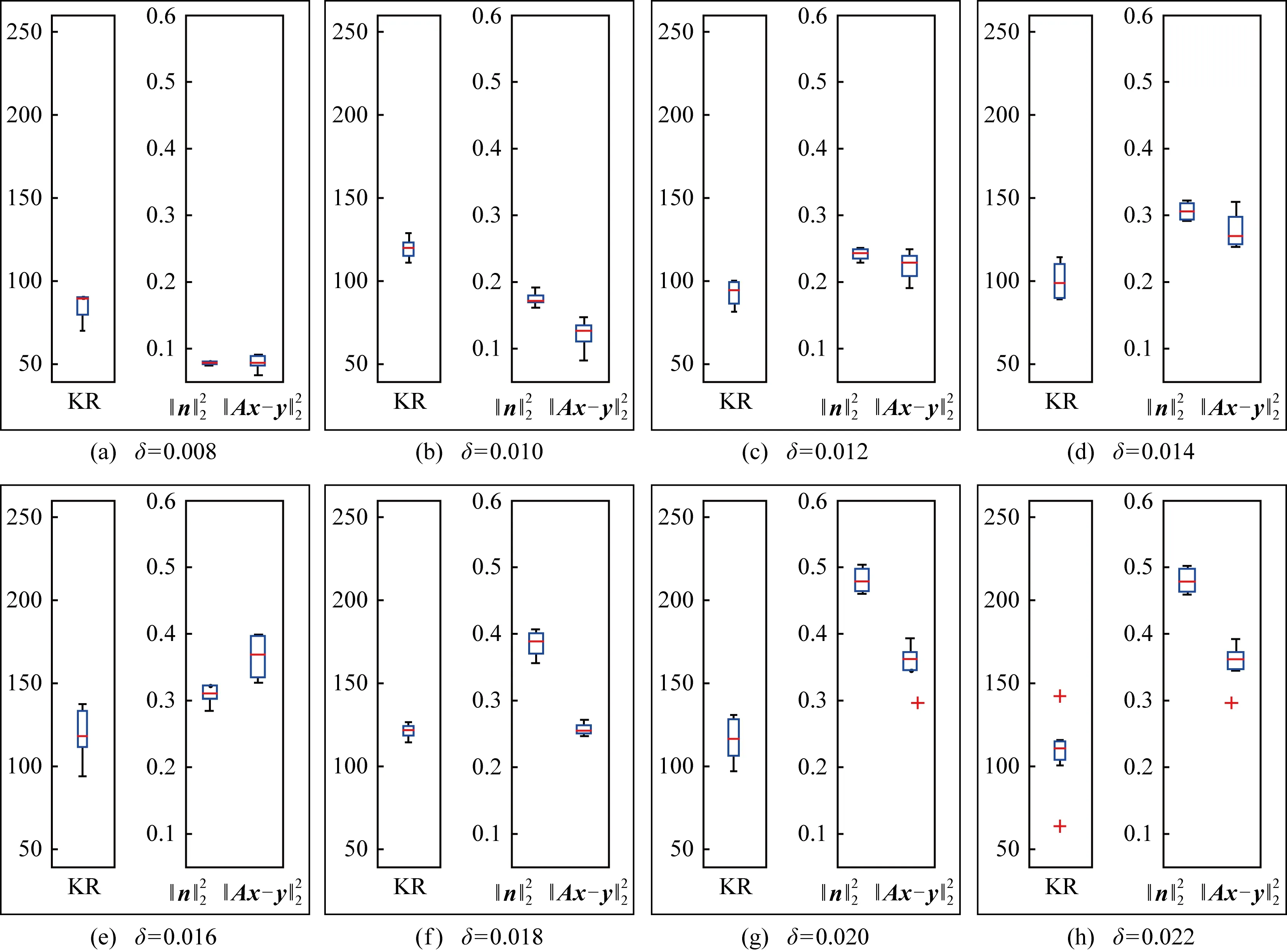
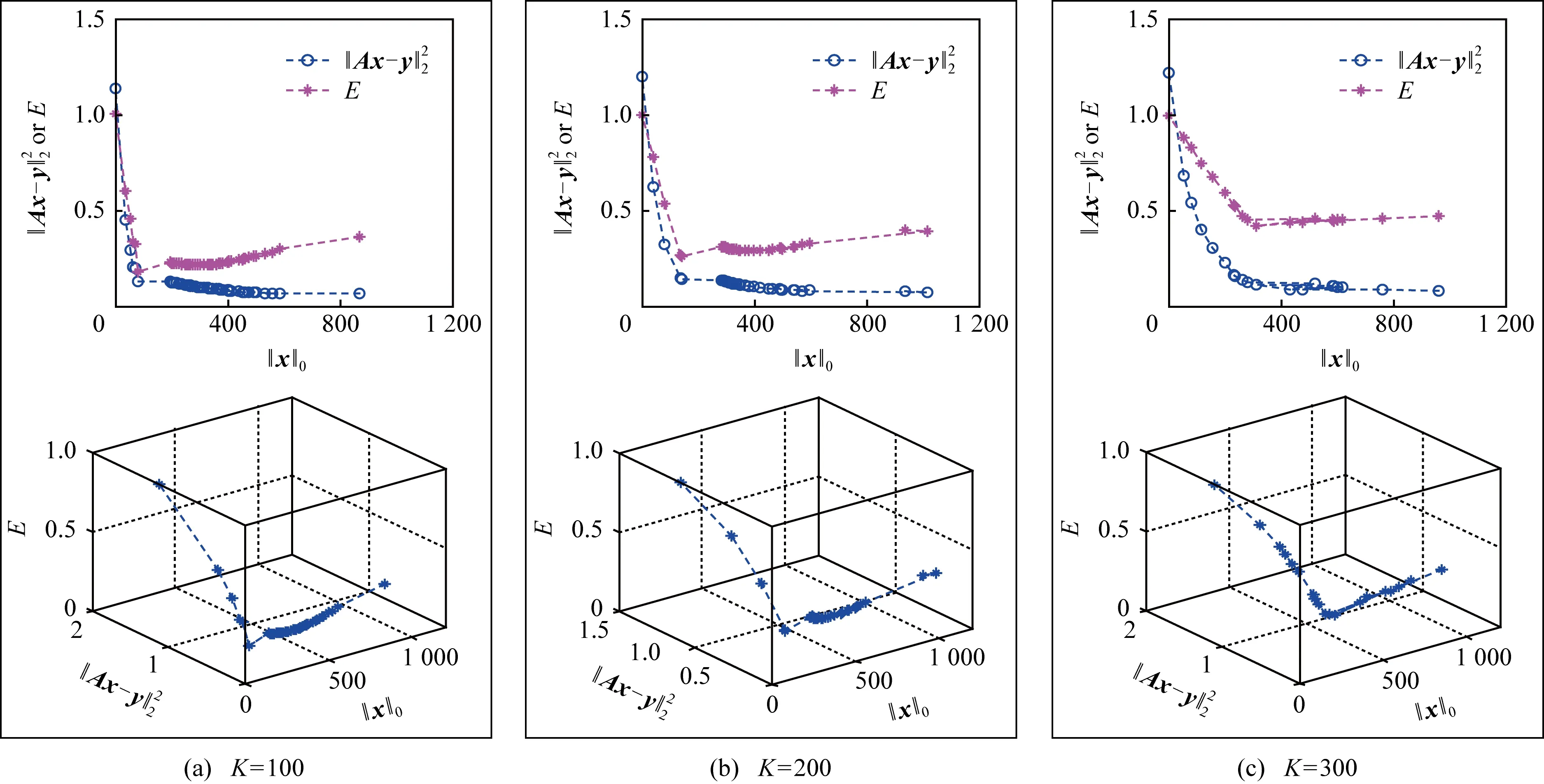
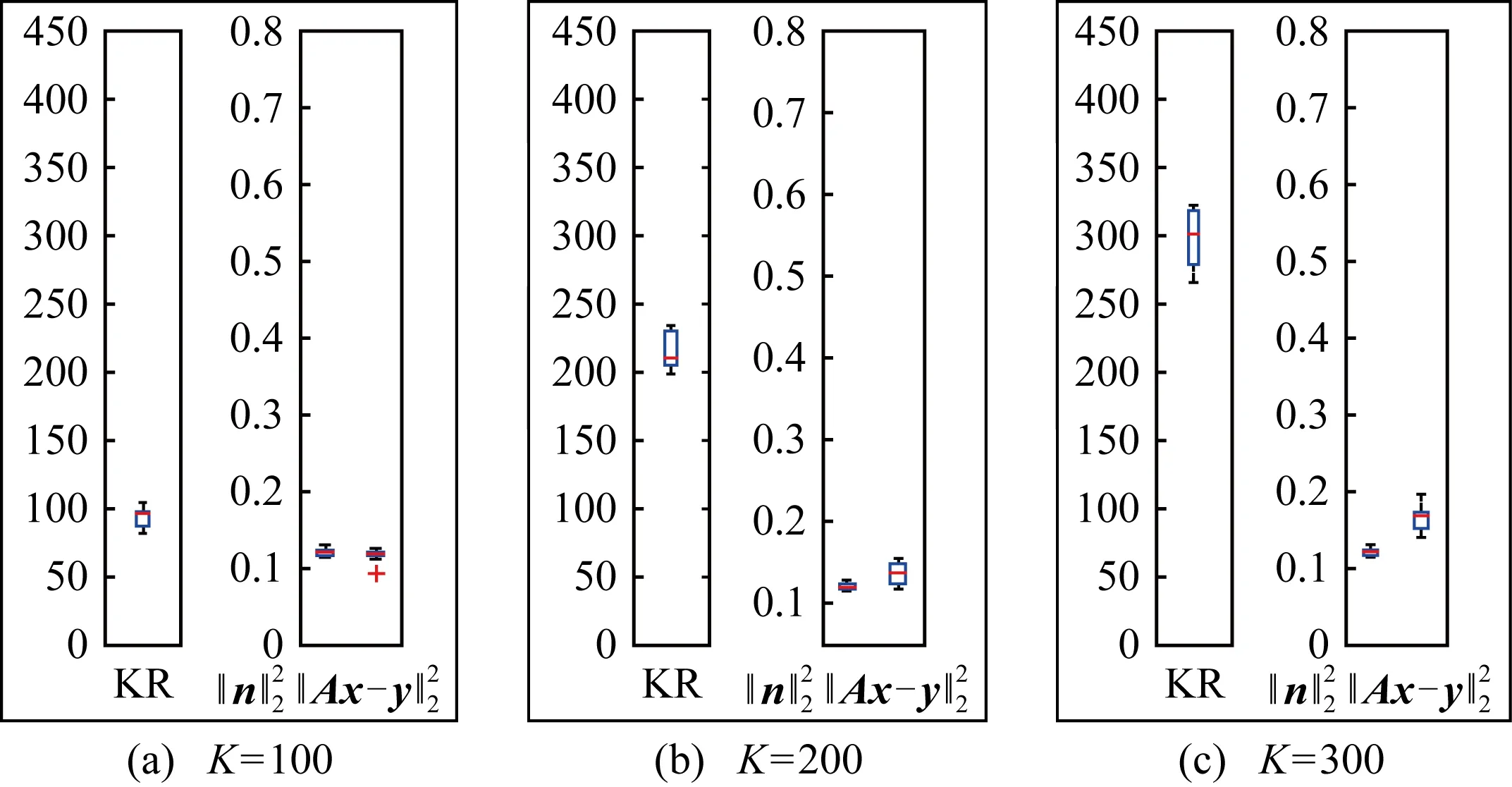
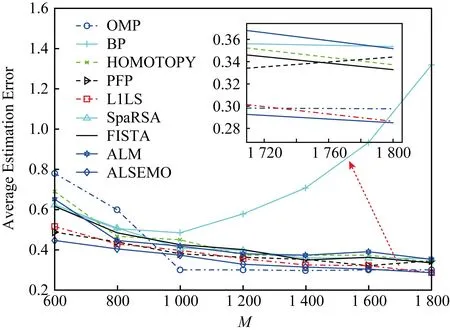
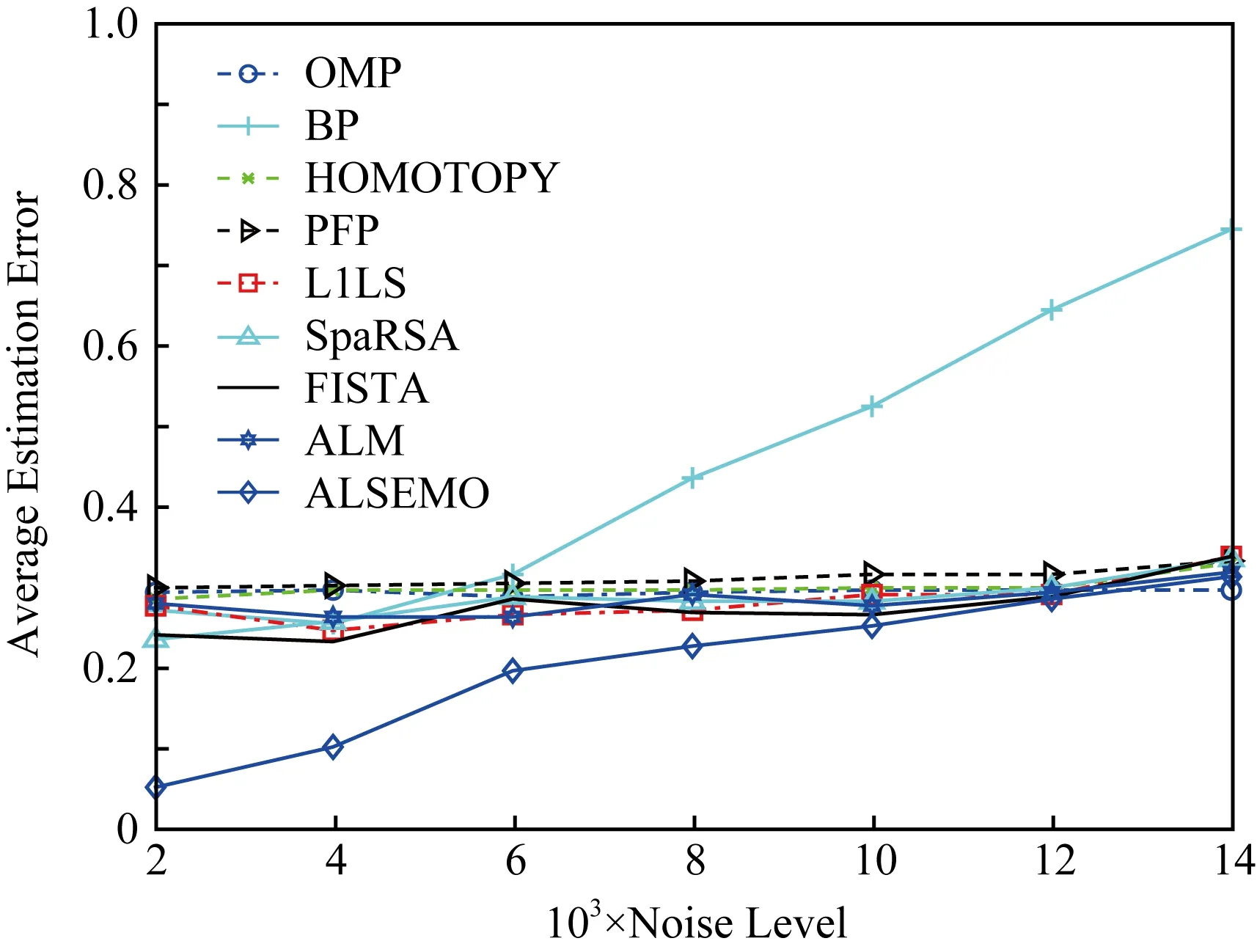
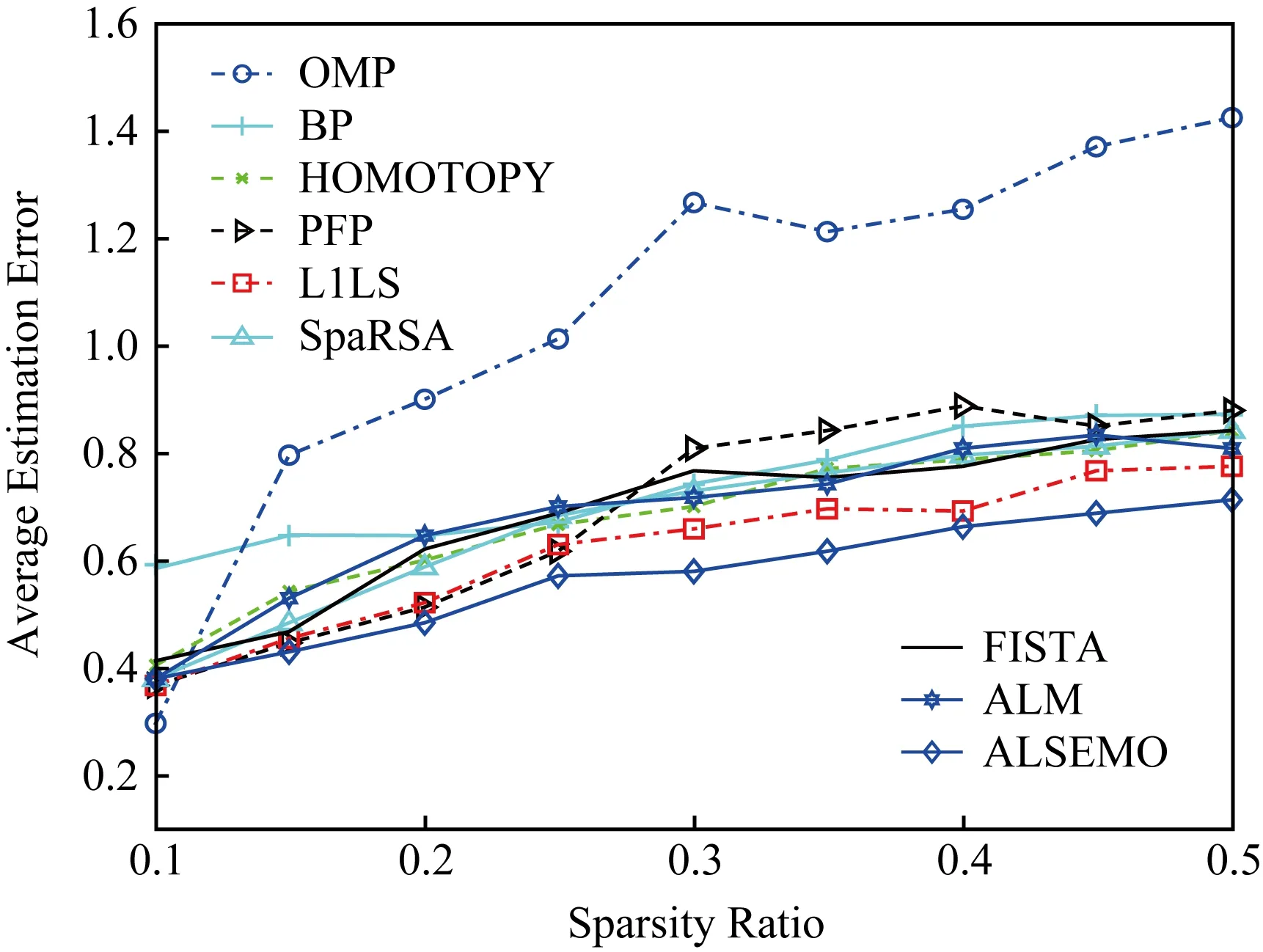
在3.2节步骤2.4中,对任意的j=1,2,…,m,如果有fj(ya) 对于稀疏优化问题,为了有效地提高解的质量,在差分进化操作后采用梯度迭代软阈值(gradient iterative soft-thresholding, GIST)的局部搜索, 这样有利于促进次优个体向最优方向进化. GIST是一个范数最小化优化方法,它可以解决问题: F(x)=f(x)+αg(x), (10) (11) (12) 为了提升解的精度,本文将3.6节中的局部搜索方法结合到进化算法中实现自适应局部搜索方法,一方面可以加速算法收敛速度从而在较短的时间内获得帕雷托最优解集(Pareto optimal set),在另一方面,有利于保持解的多样性,从而在PF有均匀的分布.自适应方法结合了2种局部搜索策略,如图1所示: Fig. 1 Adaptive local search method framework图1 自适应局部搜索方法流程 算法2.基于竞争策略的自适应算法. 输出:最优解集{x1,x2,…,xN}. 步骤1. 初始化:t1,t2=0,j=1,2,…,m,q=1,2,…,n; 步骤6. 重复步骤3与4直到k=Maxt2且k%2=0. 在差分进化操作后,算法2利用2个局部搜索方法ALS -Ⅰ和ALS -Ⅱ产生2个解,然后比较这2个解的目标函数值选出当前优胜解来更新z*和邻域信息,最后根据优胜次数选出局部搜索方法产生解. 图2描述了2种局部搜索算法竞争获得最优解的流程,其中A={xk,k=0,1,…,n}由ALS -Ⅰ产生,B={sk,k=0,1,…,n}由ALS -Ⅱ产生.它们都满足式(10),所以这2个解使得成立: (13) Fig. 2 The illustration of the optimal solutiongeneration process图2 最优解的产生流程示例 根据文献[19]有xk+1≠xk,sk+1≠sk,所以A和B中解的关系可以描述为 (14) 为了分析xk+1和sk+1的关系,首先需要计算这2个解的目标函数值: (15) 其中,k=0,1,2,…n.xk+1和sk+1是由2种方法产生的,所以有F(xk+1)≠F(sk+1).除此之外还需要考虑2种情况: 1) 当F(xk+1) F(xk+1) (16) 其中,α>0,则有f(xk+1) 2) 当F(sk+1) 如果ALS -Ⅰ在前k次迭代中竞争成功,那么按照算法2,ALS -Ⅱ生成B中的sk+1~sN将被淘汰,不在最优解集中.同理,如果ALS -Ⅱ在前k次迭代中竞争成功,则A中的xk+1~xN将不在最优解集中.具体比较过程如图2中示例所示,其中假设了一种2组解集可能存在的关系,此时2组解之间的支配关系为 {x1s1,s2x2,x3s3,x4s4,…,sk-1xk-1,xksk,xk+1sk+1,xk+2,xk+3,…,xN-1,xN}, (17) 则帕雷托最优解集可表示为 {x1,s2,x3,s4,…,sk-1,xk,xk+1,xk+2,xk+3,…,xN-1,xN}, (18) 其中,sk+1~s1已被淘汰.最后,用基于角度的方法(angle-based method)[18]在帕雷托最优解集上找到最优稀疏解. 实验分为2部分:1)证明稀疏重构问题存在KR,并且此区域的解能够使测量误差和稀疏度达到均衡;2)通过比较9种稀疏重构方法来证明了本文提出的ALSEMO算法具有更高的重构精度.为了与StEMO算法对比,本实验算法最大迭代次数为200,种群数为100,每个子问题的邻居个数为20.真实模拟信号xor是随机产生的稀疏信号,它由3个步骤产生: 1) 随机选择非零系数的子集,子集基数代表xor中的非零元素; 2) 非零元素值服从标准正态分布; 3)xor被归一化为单位长度,测量矩阵A是一个元素值服从标准正态分布的高斯随机矩阵. 4.1.1 测试M对KR的影响 高斯随机测量矩阵的维度M范围为600~1 800,间隔为200,N=2 000,x的长度n=2 000,原始信号稀疏度K=100. Fig. 3 The relations among E, , 图之间的关系 Fig. 4 The box-plots of KR, and for each M图4 每个M对应的盒图 4.1.2 测试δ对KR的影响 Fig. 5 The relations among E, , 图之间的关系 Fig. 6 The box-plots of KR, and for each δ图6 每个δ对应的盒图 4.1.3 测试K对KR的影响 在本组实验中M=1 200,N=2 000,K的取值范围为100~300,其间隔为100,δ=0.01.对于每个K,其非零元素的位置是随机的且元素值服从正态分布.随着K的增加,稀疏求解问题变得复杂困难,为此,将种群大小和最大迭代次数增加至300,以取得更好的PF和重构效果.图7显示了KR的位置随K变化情况,可以看出KR总是落在K的位置,这意味着KR中解的非零项刚好就是原始信号的稀疏度,KR可以提供一个与真实信号相近的解.对每1组K做10次独立重复实验,图8用盒图显示了不同的K对KR变化的统计结果.从图8中可以看出,KR区域中解的零范数随着K的变化而变化且其值是近似相等.另一方面,E随K的增加而增加,这是由于信号越复杂,重构越困难,精度就越低. Fig. 7 The relations among E, , 图之间的关系 Fig. 8 The box-plots of KR, and for each K图8 每个K对应的盒图 在本组仿真实验中,真实信号的产生方法和之前一样,长度为2 000.将ALSEMO算法和其他8种经典的单目标方法[30]在重构性能上进行了比较,这8种方法分别是:OMP,BP,Homotopy Method (HM),PFP,L1LS,SpaRSA,FISTA,ALM.对每1组实验,观测向量y中加入了服从N(0,0.01)分布的噪声,图9~12中每一个数据是经过10次独立重复实验后所得的平均重构误差(average estimation error),表示为Ea.比较算法中所用的容忍参数为ε=0.3,α=0.02. Fig. 9 The Ea on different M图9 不同测量维度M下的重构误差 Fig. 10 The Ea on different noise level图10 不同噪声强度δ下的重构误差 Fig. 11 The Ea on different sparsity ratio图11 不同稀疏率KN下的重构误差 Fig. 12 Performance comparison of ALSEMOwith StEMO图12 比较ALSEMO和StEMO算法性能 在图9中,稀疏率KN=0.1,M为600~1 800,间隔为200,其显示了随着M的变化Ea的变化情况,可以看出ALSEMO算法的Ea低于其他算法,但是当M在1 000~1 600之间时OMP低于ALSEMO,这是因为容忍参数ε极大地影响了OMP的重构性能,并且这些实验的选择值ε=0.3恰好是最佳选择,但是在ε取其他值时可能表现不佳.在图10中,KN=0.1,噪声δ的取值范围为0.002~0.014, 间隔为0.002.随着δ的增加,所有算法的Ea都增大,但是ALSEMO算法的Ea始终保持最低,说明ALSEMO具有更好的抗噪性能.图11显示了随着稀疏率KN的增加,所有算法的Ea都在增加,但是ALSEMO算法的Ea始终保持最小.3组实验证明了本文提出的ALSEMO算法要比其他8种算法的重构精度高,这是由于本文建立了多目标模型,采用多目标进化求解方法避免了传统求解方法中存在参数敏感的问题,从而提高了重构准确度. 图12通过比较StEMO算法来证明ALSEMO具有更低的重构误差.在图12(a)中,随着M的增加,ALSEMO和StEMO算法的Ea都在下降,但是ALSEMO总保持较低的Ea,说明ALSEMO具有更高的重构精度.这是由于ALSEMO是以MOEAD为框架,相比于StEMO 它对KR的定位更加准确,并且结合基于l和l1范数的2种局部搜索方法自适应地选择出最优解,提升了解的精度和收敛速度.在图12(b)中,两者的Ea都在增加,但ALSEMO总是低于StEMO,说明ALSEMO具有更好的抗噪性能.在图12(c)中,Ea随着稀疏率的增加而增加,但是ALSEMO总低于StEMO,这说明了ALSEMO在信号变得复杂时依然能够保持较低的重构误差.3.6 局部搜索方法
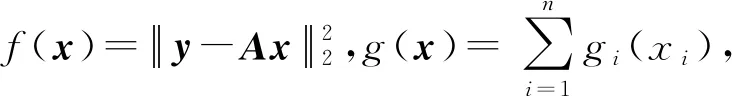


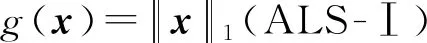
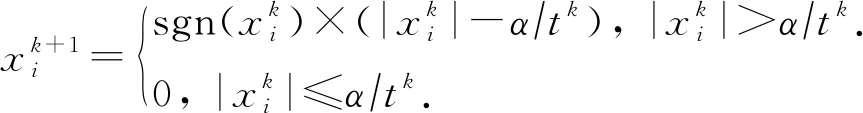
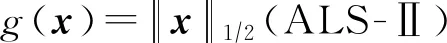
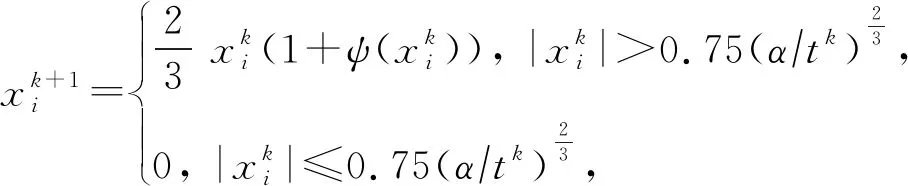
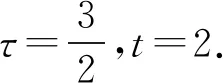
3.7 自适应局部搜索方法设计

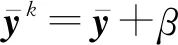
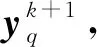
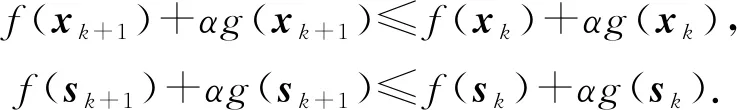

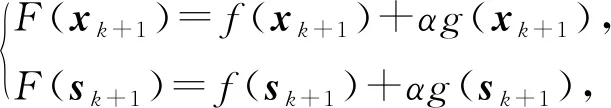
4 实验仿真与分析
4.1 测试影响KR的因素

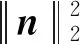
4.2 重构误差的比较与分析

5 总 结