双转子系统振动特性分析

李 超，金福艺

（长沙航空职业技术学院，湖南 长沙 410124）

目前先进航空发动机多为采用带有中介支承的双转子系统[1，2]，例如 F119、EJ200、F136、AL-31F-117S、AL-41F等。采用中介支承不仅可以减少一个承力框架，进而提高推重比，而且通过高、低压转子的反向旋转使转子系统工作过程中产生的陀螺力矩，在中介支承位置抵消一部分，避免外传[3]，大大提高了静子结构的可靠性。然而，中介支承的出现使得高、低压转子互相耦合，模态特征复杂，给分析和设计均带来一定的困难[4]。虽然众多学者对航空发动机转子系统展开研究[5-8]，但是多基于商用有限元仿真软件展开，使得对力学特征的理论分析和结构优化的方向均不够透明。马艳红[9,10]等提出了航空发动机转子系统结构效率的评估参数和计算方法，在一定程度上，可以合理的定量评价转子结构的合理性，但是未指出转子优化的方向。廖明夫等[11]提出了高压转子的结构动力学设计方法，“可容模态”[12]的设计思想可以有效降低航空发动机转子的共振峰值，但是在实际航空发动机双转子系统的应用上，依然具有一定的局限性。国外由于技术保密等原因，对航空发动机转子系统更深入一步的动力学设计理论与方法鲜有报道。

在充分总结前人经验基础上，本文建立了一种典型的带有中介支承的双转子耦合力学模型，基于拉格朗日方程获得转子系统振动微分方程解析表达式，通过解析解详细讨论了转速比和转动方向对双转子的涡动频率，不平衡响应和涡动轨迹的影响,探讨该模型对深入分析双转子的振动特性的重要意义。

1 有中介支点双转子力学模型

如图1所示的双转子模型是Lalanne M. 所提到的模型[13]延伸，其质量/刚度沿轴向是非均匀分布的对称转子系统，不计阻尼。应用拉格朗日方程,可以得到其振动微分方程。通过得到的解析解，可以得到耦合系统某些定性的运动规律和一些物理现象所涉及的影响因素，可以给出正确并具有指导意义的结论。假设：所有轴承的支承刚度均足够大（转子近似简支状态）；高压转子只做刚体运动(实际航空发动机高压转子亦是在一阶弯曲临界转速以下，做刚体运动)，则有：

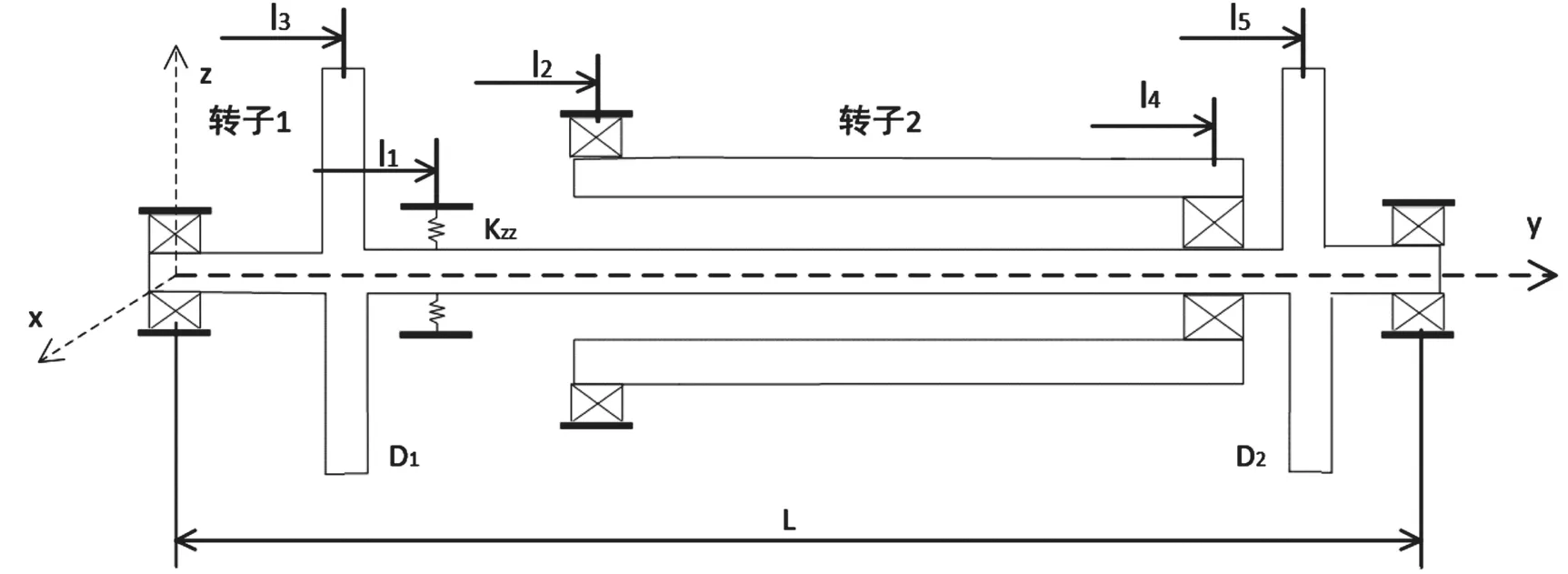
图1 双转子系统力学模型

转子1可以认为是两端简支的弯曲梁，设其中，u和w分别代表x和z方向的位移，对于该转子的求解如下：

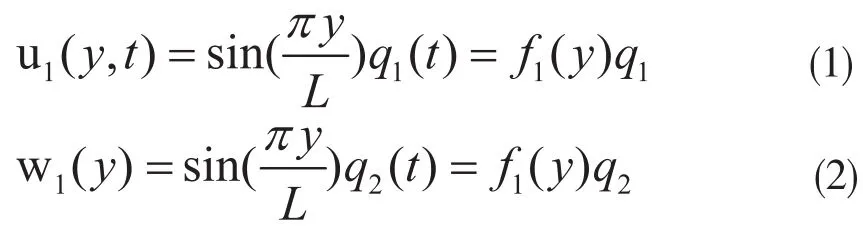
角位移如下：

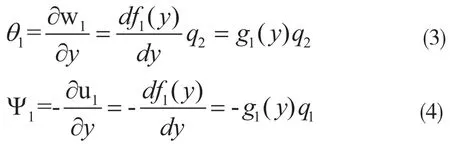
且有：

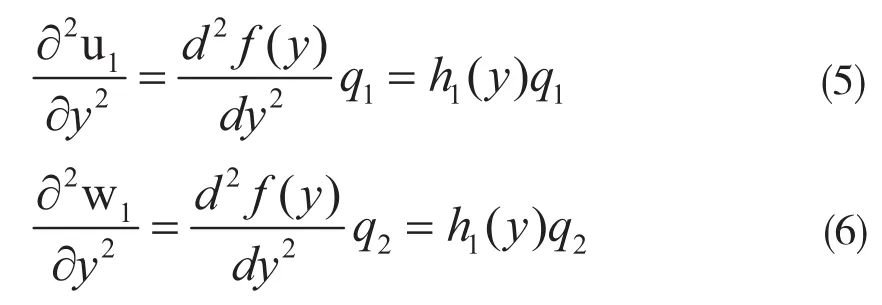
转子2假设为刚体，因此有：

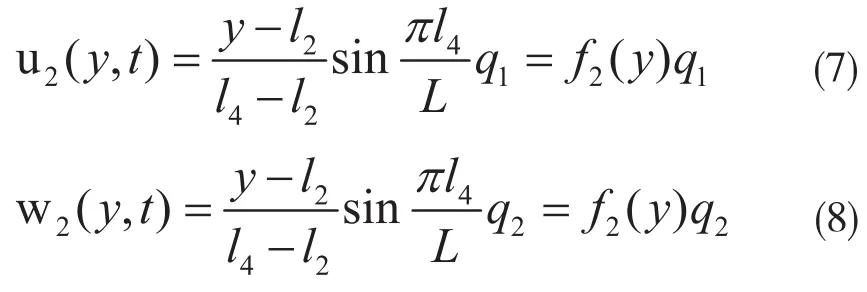
并且：

因为g2是常数，所以有：

对于盘和柔性轴动能的一般表达式为：

2 共振转速

从式（27）和（28）可以看出，共振转速除 了与广义质量m（即质量的分布形式），广义刚 度k(刚度的分布形式)有关，还与几何构形a有关。同时可以得到双转子航空发动机的共振转速随转速比n的变化规律，如图2所示。

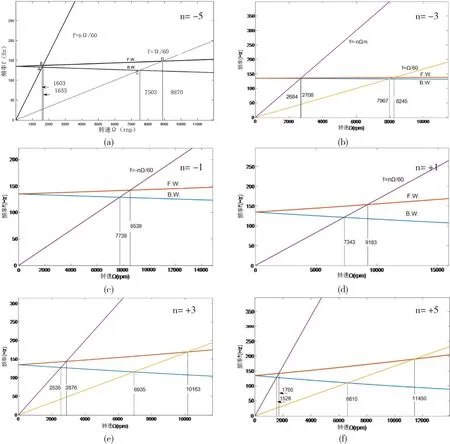
图2 坎贝尔图

对于C,D两点，有：

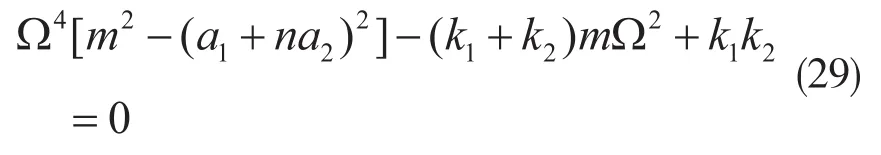
对于A,B两点，有：

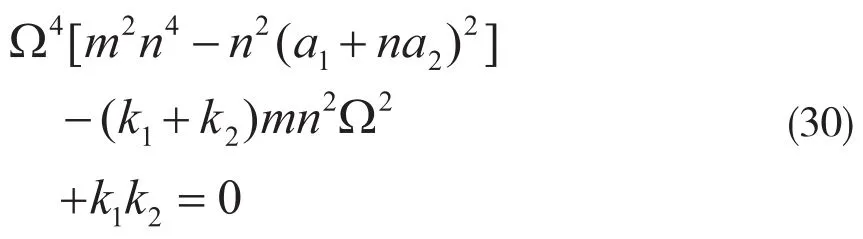
联立式（27）和式（28）可以求出相应的共振转速，已标于各图中。

观察图2可得，当两个转子反向旋转时，随着转速比增加，转子1和转子2所经过正进动和反进动的临界转速之间距离加大，且两个转子最外侧的临界转速出现两边靠拢的趋势，即转子2激起的反进动临界转速越来越小，转子1激起的正进动越来越大，而两个转子中间两个临界转速则向中间靠，即转子1激起的正进动临界转速变大，转子2激起的反进动临界转速变小。

通过比较同转速下的正转和反转可知，正转激起的正进动临界转速更大，一般不激起反进动，这是因为两个转子正转时，陀螺力矩的作用使转子刚性增加，所以增大了临界转速，这是符合实际的。

3 不平衡响应

将偏心不平衡分别加在转子1和转子2上。

3.1 转子1的不平衡响应

系统的振动微分方程如式(24)和(25)，不平衡力如式(20)和(21)。则方程解具有如下形式：

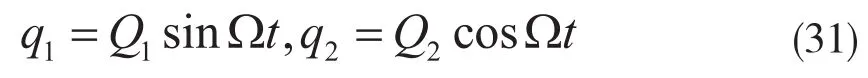
代入振动微分方程，可以解得：

式中：m1为不平衡质量。

相应的临界转速为：

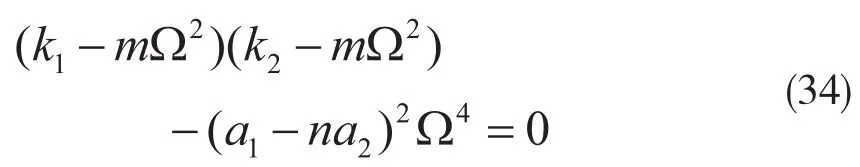
这与式(30)是相同的。

当高、低压转子的转速比n=-5，n=-1，n=+1，n=+5时，相应的不平衡响应如图3所示。

3.2 转子2的不平衡响应

系统的振动系统的振动微分方程如式(24)和(25)，不平衡力具有同式(20)和(21)相同的形式。方程解同样具有形如式(31)的形式，可以解得：

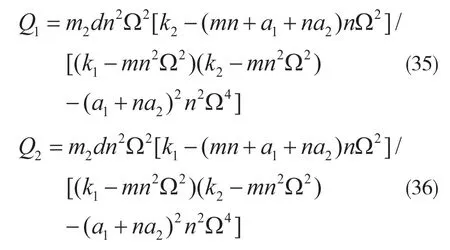
相应的临界转速为：

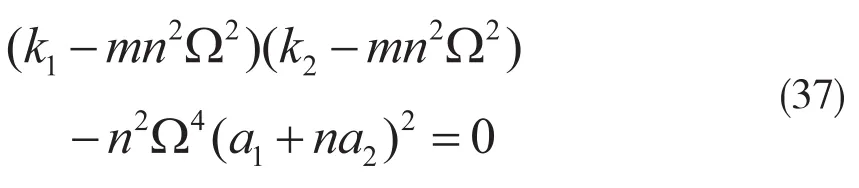
这与式(29)是相同的。

当高、低压转子的转速比n= -5，n= -1，n=+1，n= +5时，相应的不平衡响应如图4所示。

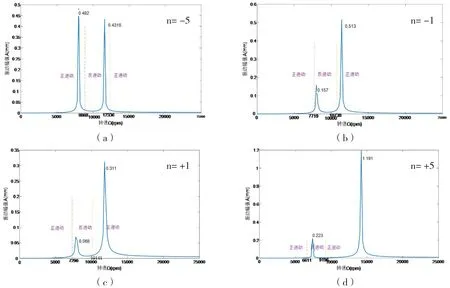
图3 转子1上的不平衡响应

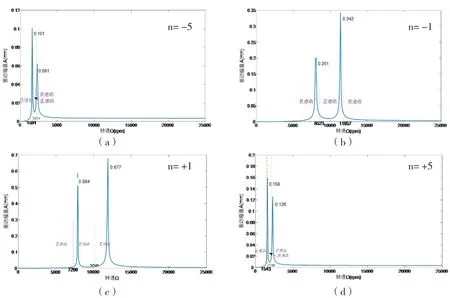
图4 转子2上的不平衡响应

以图4可以看出，当转子1（低压转子）上存在不平衡量：反向旋转时，随着转速比的提升，正反进动区域线（图中虚线）右移，进动方向由反进动变为正进动，且第一次共振峰值明显增加。正向旋转时，随着转速比的提升，正反进动区域线（图中虚线）左移，转子1的两阶共振峰值均明显增加。当转速方向由反向变为正向时，两个共振峰值之间的距离明显增加，且当两个转子正向旋转时，随着转速比的增加，共振峰值间的距离也明显增加，这对双转子系统来说是不利的。以上可以看出，正向旋转且转速比较小时，可有效减小转子1上的振动峰值。反向旋转且转速比较小时，可有效减小共振频率间距。

当转子2（高压转子）上存在不平衡量：反向旋转时，随着转速比的提升，正反进动区域线左移（图中虚线），共振频率和振动幅值明显降低，共振频率间距明显减小。正向旋转时，随着转速比的提升，正反进动区域线左移（图中虚线），共振频率和振动幅值明显降低，共振频率间距明显减小。兼顾转子2振动峰值和共振频率间距，应选择反向旋转且转速比较大好一些，当然这对转子1是不利的。因此，转速比的选取应同时兼顾转子1和转子1。

需要注意的是，实际航空发动机高低压转速之间的关系并非线性，因受气动条件的限制，高低压转子之间的转速关系十分复杂。

4 涡动轨迹

两个向量的叉积：

4.1 转子1上的不平衡量

当不平衡量在转子1上时，根据式(32)(33)和式(39)可得：

4.2 转子2上的不平衡量

图6 转子2存在不平衡质量时的涡动轨迹(a)n＜-a1/a2 (b)-a1/a2＜n＜0 (c)n＞0

表达式(56)和(58)相同，但是其涡动轨迹不同。当如图6所示。

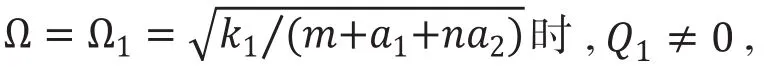
本小节给出了计算涡动轨迹的方法，由此可以预算转子在任意转速下的运动轨迹，可以通过调整转速使涡动幅值达到合理的设计值（当也可以通过简单的临界转速函数的零点估计涡动轨迹转型（由正进动变为反进动，或由反进动变为正进动）的位置，这些方法对实际航空发动机转子设计是有益的。

5 结论

本文首次搭建起基于假设的双转子系统理论解析力学模型，避开了数值仿真计算，可以比较清晰的解释双转子系统内部运动规律，对航空发动机双转子系统结构方案的初始布局设计具有较大的指导意义；转速比（包括转动方向）对航空发动机双转子系统的振动特性具有较大的影响，可以通过改变转速比，进而对共振频率，涡动轨迹进行调节，合理选取转速比可以有效地调节共振转速的配置，可以减小振动幅值。

根据本文所提出的双转子力学模型，可以进一步计算其应变能，探索转子结构的不同的质量、刚度分布对应变能分布形式的影响，这对转子的总体结构设计是有意义的。