分层结构颗粒堆积床内的流动阻力特性
2019-07-11李良星王凯琳谢伟张双宝
李良星,王凯琳,谢伟,张双宝
(西安交通大学动力工程多相流国家重点实验室,710049,西安)
多孔介质内的单相/两相流动常见于众多学科与领域中,涉及核反应堆工程、化工过程、油气田开发工程等[1-2]。在核反应堆发生堆芯熔融严重事故后,若堆芯熔融材料与堆内冷却水接触,就可能发生破碎,并形成具有多孔介质结构的颗粒碎片堆积床。自美国三哩岛严重事故发生后,国内外进行了大量实验来研究分析碎片床的冷却特性[1-6]。Ma等认为,颗粒堆积床内流动阻力对碎片床冷却性能有至关重要的影响[7]。然而,已有的研究多是基于均匀堆积结构的颗粒床进行实验,针对非均匀堆积颗粒床的研究还比较少,且多为研究颗粒堆积床内传热特性及其干涸热流密度[2-5],对分层结构颗粒堆积床内流动阻力的研究较少[6]。事实上,Karbojian等开展的燃料-冷却剂相互作用(FCI)实验研究结果[8-9]表明,颗粒床的分层堆积结构是常见的碎片床堆积方式之一,如图1所示。

图1 FCI实验中形成的分层颗粒床[8]
为了进一步深入探究具有分层结构的颗粒堆积床内的单相/两相流动特性,本文在前期研究[6]的基础上,使用4种尺寸的球形颗粒分别构建了3种堆积结构的颗粒床,开展了颗粒堆积床内的单相(水)和空气-水两相流动实验,对比分析了不同堆积结构颗粒床内的流动阻力特性,并基于实验数据,验证了常用的碎片床冷却性分析模型。
1 实验系统和方法
1.1 实验装置
为了研究堆积颗粒床内的流动特性,西安交通大学动力工程多相流国家重点实验室设计和搭建了碎片床冷却性实验系统(DEBECO),实验系统如图2所示,图3是实验测试段结构图。
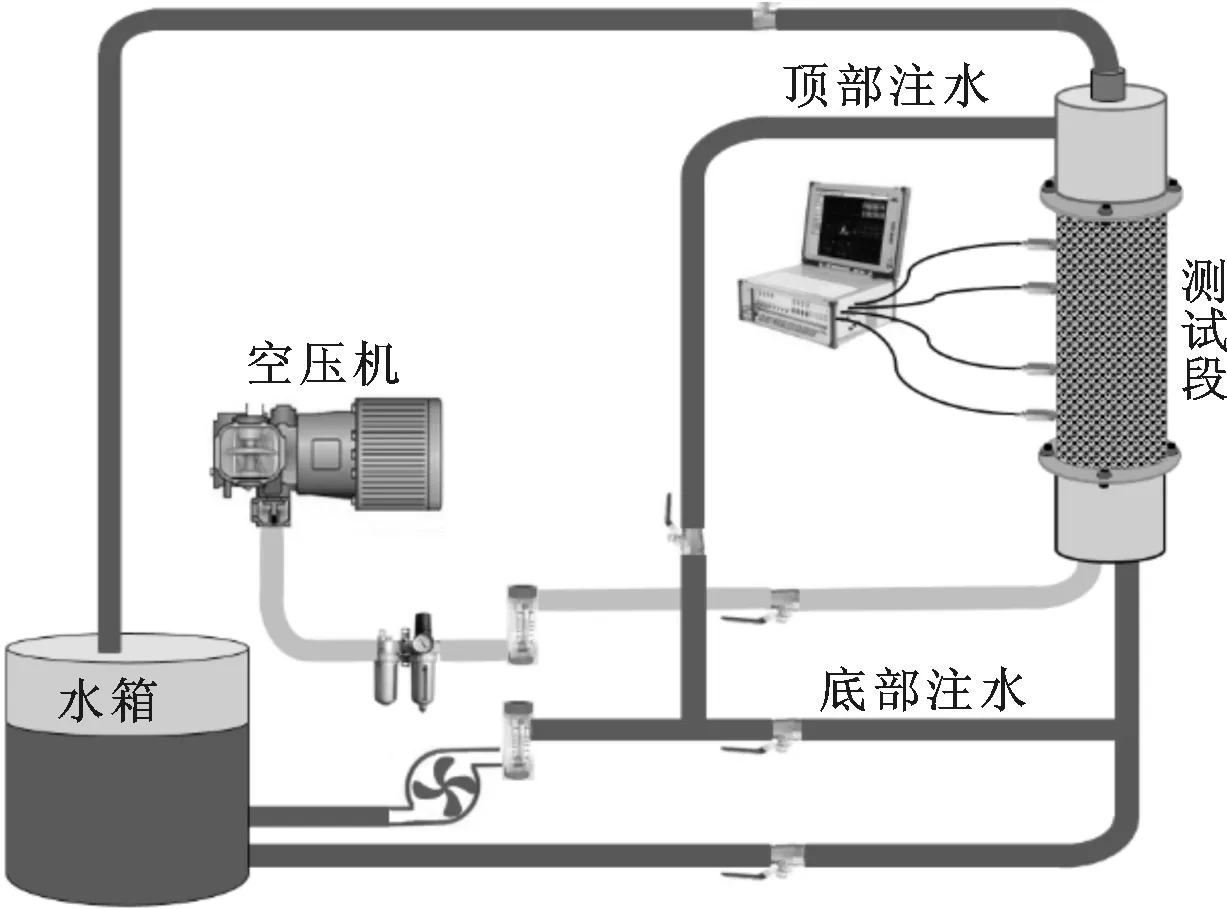
图2 DEBECO实验系统图

图3 实验测试段结构图
实验系统由集水箱、水泵、空压机、气水均匀混合段、实验测试段及数据采集系统构成。实验测试段为圆柱形有机玻璃管,内径120 mm、高度600 mm、外径130 mm。在实验测试段的顶部和底部的法兰连接处分别放置不锈钢网栅,用于固定颗粒堆积床。实验采用Omega高精度压力传感器测量记录实验段内不同位置测点的压力;采用不同量程范围的Rosemount3051压差变送器测量实验段不同高度下的流动压差动态信号,压力传感器和差压变送器的精度分别为0.25%和0.04%。使用不同量程的OMEGA流量计(FL-2000系列)测控空气和水的流量,测量精度为2%。通过K型热电偶测量水和空气的温度,用于计算流体的黏度和密度。实验均在大气压(约0.1 MPa)和室温(约20 ℃)条件下运行。实验过程中使用NI数据采集系统对温度、压力等信号进行采集整理。
1.2 实验颗粒床
本文使用4种尺寸的球形颗粒(下文分别用1.5 mm颗粒、2 mm颗粒、6 mm颗粒、8 mm颗粒表示)构建了9个颗粒堆积床,分别命名为Bed-1~Bed-9,具体信息如表1所示。实验段内颗粒堆积方式采用自由堆积,堆积颗粒通过锥形漏斗倒入实验测试段。锥形漏斗尾部连接软管,堆积颗粒由实验测试段底部逐渐堆积至顶部。Bed-1~Bed-4是由单一尺寸颗粒构建的颗粒均匀堆积床,Bed-5~Bed-9是由两种不同尺寸颗粒构建的水平分层堆积床,两种尺寸颗粒各占实验测试段体积的一半。其中,Bed-5~Bed-8是水平分层颗粒堆积床,Bed-9是竖直分层颗粒堆积床。图4为水平分层和竖直分层颗粒堆积床结构示意图。
孔隙率通过称量法获得,表达式如下
(1)
式中:V0是实验段总体积;ms是实验段内填充颗粒的质量;ρs是填充颗粒密度。实验中使用精度为0.1 g的称量计测量装入实验测试段的颗粒质量,进而获得堆积颗粒的体积。基于实验测试段的体积,获得颗粒堆积床的孔隙率。

表1 不同实验床的信息
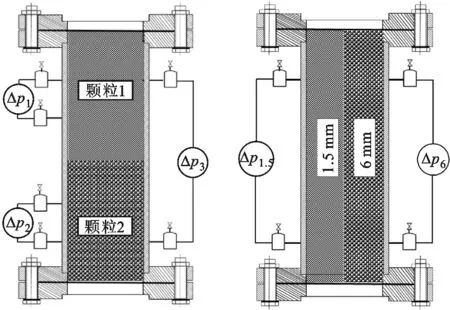
(a)水平分层堆积床 (b)竖直分层堆积床图4 颗粒堆积床示意图
2 颗粒床内流动阻力模型
基于大量实验研究,许多学者提出了不同的碎片床冷却性分析模型。对球形颗粒堆积床的单相流动,工程界普遍认为半经验公式Ergun方程[10]可以很好地预测其流动阻力压降,计算值与实验值的平均偏差低于10%[11-14]。Ergun方程表达式如下
(2)
式中:dp/dz是颗粒堆积床内沿高度方向的阻力压降;等号右侧第1项为黏滞力损失,第2项为惯性力损失;μ是流体动力黏度;ρ是流体密度;J是流体表观速度;K和η为渗透率和穿透率;150和1.75为Ergun常数;d是颗粒的直径;ε为多孔介质床的孔隙率。
基于Ergun方程,Lipinski等通过引入相对渗透率Kr、相对穿透率ηr和相间摩擦力Fi,提出了颗粒堆积床内的两相流动阻力模型[15]
(3a)
(3b)
式中:下标l和g分别代表液相和气相;α为截面含气率。表2总结了碎片床冷却性分析常用的两相流动阻力模型的基本参数。
表2中,Schulenberg-Müller模型的相间摩擦力表达式为[16]
(4)
Tung-Dhir模型则针对不同流型分别给出了相间摩擦力的表达式[17]
(5a)
(5b)

(5c)
注:s=1-α。
从表2可以看出,不同的模型对参数Kr、ηr和Fi选取了不同的表达式。总体上,Lipinski[15]、Reed[18]和Hu-Theofanous[19]模型未考虑相间摩擦力的影响(Fi=0),而Schulenberg-Müller[16]和Tung-Dhir[17]模型则特别考虑了相间摩擦力的影响,甚至基于不同的流型给出了不同的表达式,这给工程计算和应用带来极大的不确定性。因此,本文将基于均匀堆积床和竖直分层堆积床内两相流动阻力的实验结果,进一步验证常用的颗粒堆积床内两相流阻力模型。
3 实验结果及分析
3.1 颗粒均匀堆积床的单相流动实验
首先进行了颗粒均匀堆积床内的单相流动实验,图5给出了单相水竖直向上流过单尺寸颗粒堆积床Bed-1~Bed-4时测量的流动阻力压降,同时给出了Ergun方程的计算值。从图5可以看出:颗粒均匀堆积床内的单相流动阻力压降随着水的流速增加而逐渐增大,相同流速下,堆积颗粒尺寸越小(Bed-1),其单相流动阻力压降越高;总体上,Ergun方程的计算值与所有颗粒均匀堆积床Bed-1~Bed-4的实验测量阻力压降吻合较好,平均相对偏差均低于7%。
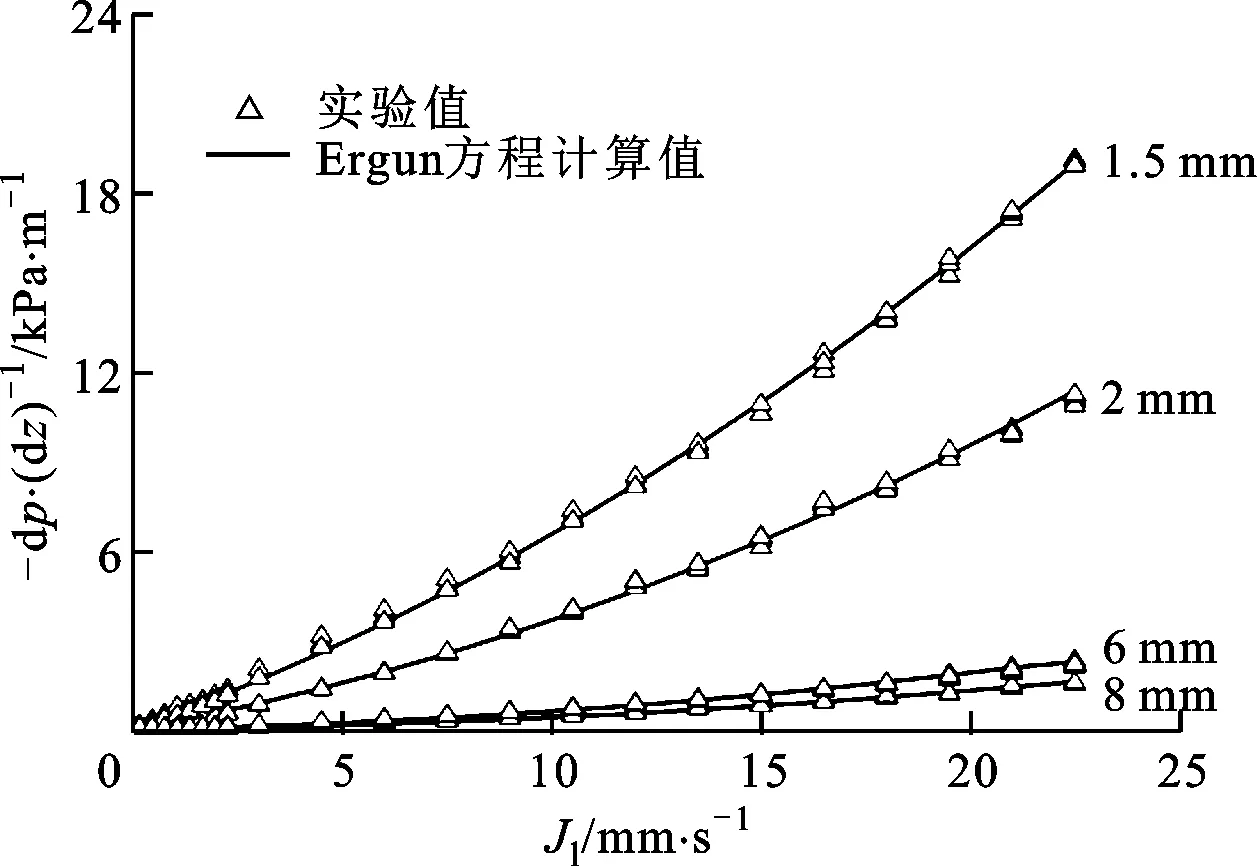
图5 颗粒均匀堆积床单相流动阻力压降
3.2 水平分层颗粒堆积床的单相流动实验
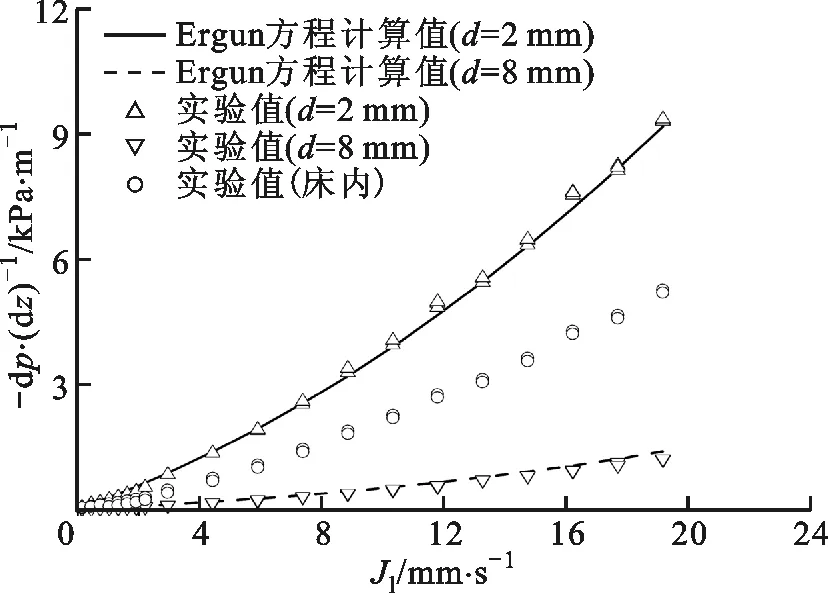
图6a~6d分别显示了具有水平分层结构的颗粒堆积床Bed-5~Bed-8的单相流动阻力压降测量值和Ergun方程计算值,其中,Bed-5和Bed-6由1.5 mm和6 mm两种颗粒组成,Bed-7和Bed-8由2 mm和8 mm颗粒组成。压降测量示意图如图4a所示,Δp1表示上半层测量得到的流动阻力压降,Δp2表示下半层的流动阻力压降,Δp3则表示分层颗粒堆积床的流动阻力压降。
图6a给出了1.5 mm颗粒堆积在下层、6 mm颗粒堆积在上层时水平分层颗粒堆积床Bed-5的单相流动阻力压降。如图中所示,实验段上层和下层的单相阻力压降均和Ergun方程的计算值吻合较好,说明大颗粒在上、小颗粒在下的分层结构对颗粒堆积床内各部分的单相流动阻力影响较小。图6c给出了2 mm颗粒堆积在下层、8 mm颗粒堆积在上层时的单相流动阻力压降及其与Ergun方程计算值的对比,显示了同样的结果。

(a)Bed-5
(b)Bed-6
(c)Bed-7

(d)Bed-8图6 水平分层颗粒堆积床的单相流动阻力压降
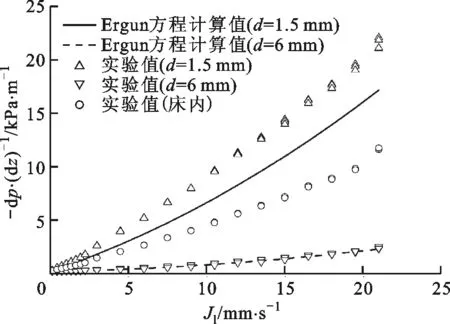
图6b给出了6 mm颗粒在下层、1.5 mm颗粒在上层时水平分层颗粒堆积床Bed-6的单相流动阻力压降。如图所示,下层大颗粒床内单相流动阻力压降与Ergun方程的计算值基本一致,平均相对偏差为3%。然而,上层小颗粒堆积床内的单相流动阻力压降明显高于Ergun方程计算值,平均相对偏差为27%。与相同工况下小颗粒均匀堆积床相比,这种水平分层结构显著提高了上层小颗粒堆积床的流动阻力压降,且随流速升高,阻力压降提高得越多,在最大的实验流速工况下,上层小颗粒堆积床的流动阻力压降约是小颗粒均匀堆积床流动阻力压降的1.25倍。同样地,图6d显示了8 mm颗粒在下、2 mm颗粒在上的分层堆积床Bed-8的实验结果,显然,上层小颗粒堆积床内的单相流动阻力压降高于Ergun方程计算值,平均相对偏差为23%,而下层大颗粒堆积层的单相流动阻力压降与Ergun方程计算值吻合较好。由此可以得出,大颗粒堆积在下层而小颗粒堆积在上层时,分层结构会显著提高上层小颗粒堆积床内的流动阻力压降。分析认为,当流体从大颗粒层进入小颗粒层时,由于下层大颗粒堆积床内的孔隙率较大而上层小颗粒堆积床的孔隙率较小,流道突缩现象可能会在分层界面处产生流动阻力,进而提高了上层小颗粒堆积床内的流动阻力压降。
已有的研究表明,碎片床中流动阻力升高会导致碎片床干涸热流密度下降,碎片床的可冷却性降低[20-21]。Konovalikhin和Thakre等在基于颗粒分层堆积床进行的传热实验中发现,对大颗粒在下层、小颗粒在上层的分层结构,小颗粒层的干涸热流密度明显低于相同尺寸小颗粒均匀堆积床的干涸热流密度[22-23],这进一步验证了本文的研究结论。
同时,从图6中可以看出,水平分层结构中,无论下层是由较大尺寸的颗粒组成还是由较小尺寸的颗粒堆积,下层颗粒床的单相流动阻力压降均与Ergun方程的计算结果有良好的一致性。由此可知,当流体竖直向上流过分层堆积颗粒床时,水平分层结构几乎不会对下层颗粒床的流动阻力压降产生影响。
3.3 竖直分层颗粒堆积床的单相流动实验
竖直分层颗粒堆积床Bed-9中,实验测试段左半部分由1.5 mm颗粒组成,其实验测量压降用Δp1.5表示,右半部分为6 mm颗粒,使用Δp6表示实验测量压降,左右两层界面处颗粒直接相互接触。图7绘制了单相水竖直向上通过竖直分层颗粒堆积床的单相流动阻力压降,为便于对比,同时给出了相同尺寸颗粒均匀堆积床Bed-1和Bed-3的实验测量单相阻力压降。
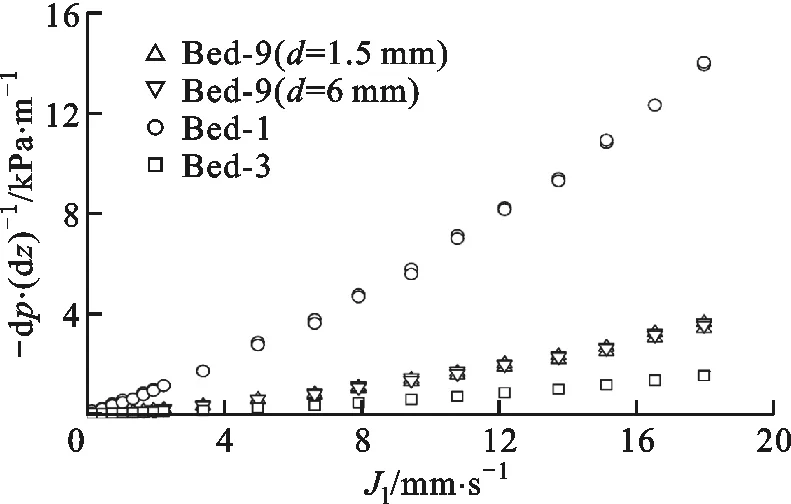
图7 Bed-9的单相流动阻力压降及其与Bed-1和Bed-3的对比
由图7可以看出,Bed-9中左半部分(1.5 mm颗粒层)的测量压降与右半部分(6 mm颗粒层)的测量压降相同。总体上,竖直分层床的单相阻力压降低于1.5 mm颗粒均匀堆积床Bed-1的流动阻力压降,但略高于6 mm颗粒堆积床的流动阻力压降。
分析认为,当流体自下而上经过竖直分层颗粒床时,由于小颗粒堆积层的孔隙率相对较小,一部分流体可能会由小颗粒层横向流向孔隙率较高的大颗粒堆积层,进而导致小颗粒堆积层内的总流量降低而大颗粒堆积层内的流量升高。换而言之,不同于颗粒均匀堆积床内的一维流动现象,竖直分层颗粒床内不仅存在竖直向上的流动,还可能存在水平方向的横流,多维流动现象导致竖直分层颗粒堆积床内的流动阻力压降明显不同于均匀颗粒堆积床。因此,竖直分层结构对颗粒堆积床内的流动阻力产生了重要影响,需要进一步深入研究。
3.4 竖直分层颗粒堆积床的两相流动实验
在Bed-9单相流动实验的基础上,进一步开展了空气-水两相竖直向上的两相流动实验。实验过程中,首先调整液速到设定工况下,然后保持液速不变,逐渐增加气体速度,并记录不同流速下的两相流动阻力压降。当一个实验工况结束时,调整液速,重复上述实验步骤,进行下一组实验。
图8显示了液速为0.3 mm/s时竖直分层颗粒堆积床内的两相流动阻力压降。为便于对比,图8中也给出了相同两相工况下颗粒均匀堆积床Bed-1和Bed-3的实验测量两相流动阻力压降。

图8 Bed-9的两相流动阻力压降及其与Bed-1和Bed-3的对比
如图8所示,当液速保持不变时,颗粒均匀堆积床Bed-1的两相流动阻力压降随流速升高而逐渐升高,而6 mm颗粒均匀堆积床Bed-3在实验工况范围内,其两相流动阻力压降随流速升高呈现出下降趋势。已有的研究表明,这主要是由于在较大尺寸颗粒堆积床(如Bed-3)内,相间摩擦力对两相流动阻力压降产生重要影响,导致其两相流动阻力压降降低,而在小尺寸颗粒堆积床(如Bed-1)内,相间摩擦力的影响可以忽略,其两相流动阻力压降随流速升高而逐渐升高[12]。
对竖直分层颗粒堆积床,在较低流速下,两相流动阻力压降随流速增加先降低后升高。总体上,竖直分层颗粒堆积床Bed-9的两相流动阻力压降低于小尺寸颗粒均匀堆积床Bed-1,但高于大尺寸颗粒均匀堆积床Bed-3。总体而言,气速越大竖直分层颗粒堆积床Bed-9的流动阻力压降与均匀堆积床Bed-1和Bed-3的流动阻力压降差值越大,在实验工况的最大流速时,竖直分层颗粒堆积床Bed-9的流动阻力压降约是小尺寸颗粒均匀堆积床Bed-1流动阻力压降的50.5%,是大尺寸颗粒均匀堆积床Bed-3流动阻力压降的3.2倍。基于竖直分层颗粒堆积床单相流动实验的分析结果,可以认为竖直分层颗粒床内存在水平和竖直两个方向的多维流动现象,且对颗粒堆积床内的两相流动阻力产生了重要影响,需要进一步深入研究。
为了验证颗粒堆积床两相流动阻力分析模型对竖直分层颗粒堆积床内两相流动阻力压降计算的准确性,图9和图10分别对比了表2中不同模型基于Bed-1和Bed-3的计算值和Bed-1、Bed-3及Bed-9的两相流动阻力压降实验值。总体上,表2中Lipinski[15]、Reed[18]和Hu-Theofanous[19]模型没有考虑相间摩擦力的影响,而Schulenberg-Müller[16]、Tung-Dhir[17]、Li等[12]的模型则特别给出了相间摩擦力的表达式。
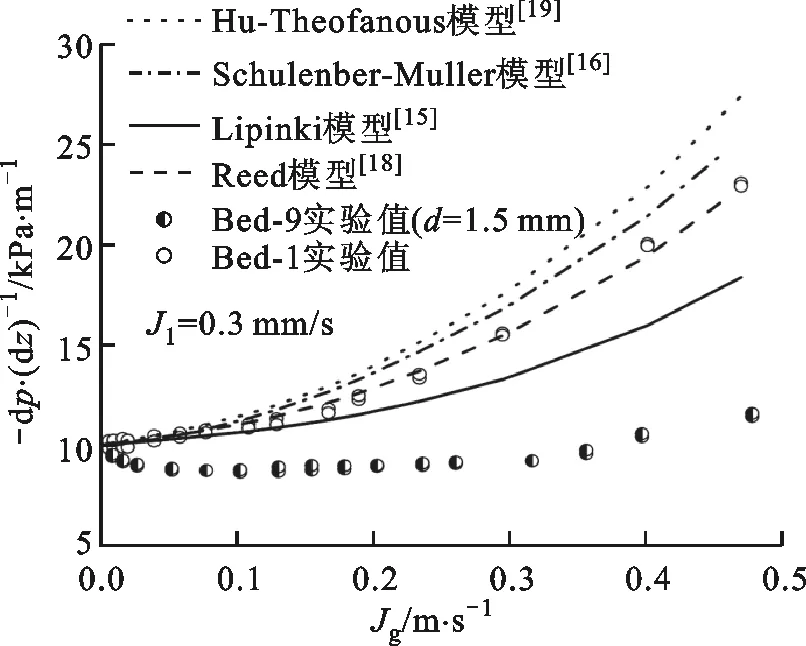
图9 两相流动阻力分析模型基于Bed-1的计算值与Bed-1和Bed-9的实验值对比
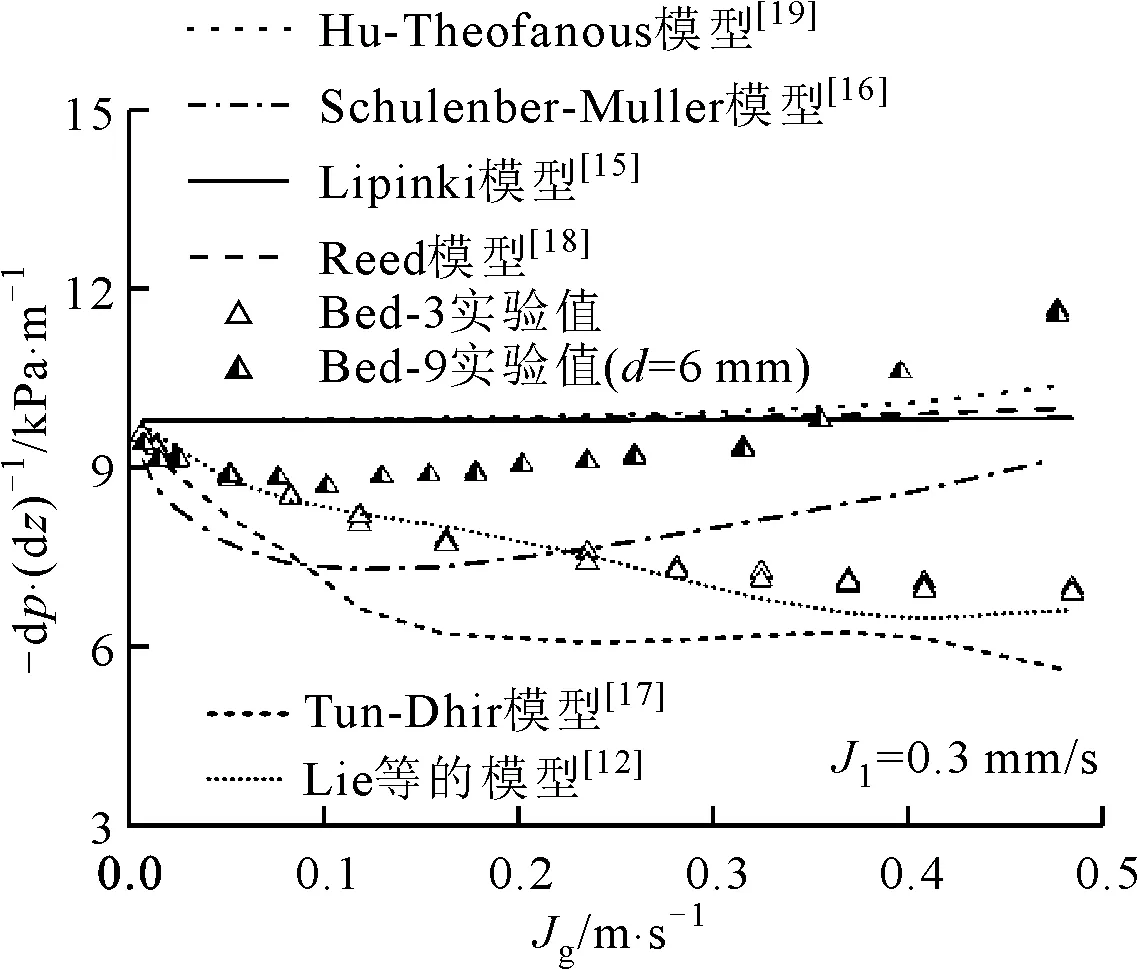
图10 两相流动阻力分析模型基于Bed-3的计算值与Bed-3和Bed-9的实验值对比
从图9中可以看出,对1.5 mm颗粒均匀堆积床,无论是否考虑相间摩擦力,所有模型的计算结果和实验数据均呈现相同的上升趋势,说明此时相间摩擦力的影响较小。其中,Hu-Theofanous[19]和Schulenberg-Müller[16]模型的计算值明显高于实验值,而Lipinski模型[15]的计算值低于实验值。总体上,Reed模型[18]的计算值与实验数据吻合较好。然而,所有模型的计算值明显高于竖直分层颗粒堆积床Bed-9的两相流动阻力压降实验值。
如图10所示,与实验测量的Bed-3两相流动阻力压降逐渐降低的变化趋势不同,忽略了相间摩擦力的模型如Lipinski[15]、Reed[18]和Hu-Theofanous[19]模型计算获得的两相流动阻力压降随流速升高而逐渐升高,而考虑了相间摩擦力的模型如Schulenberg-Müller[16]、Tung-Dhir[17]和Li等[12]的模型则预测出了与实验数据类似的阻力压降下降趋势。这说明此时相间摩擦力对两相流动阻力影响较大,较大尺寸颗粒堆积床的两相流动阻力模型须考虑相间摩擦力的影响。总体上,Schulenberg-Müller[16]和Tung-Dhir[17]模型的计算值与实验数据有显著偏差,Li等[12]的模型的计算结果与实验数据吻合较好。然而,上述所有模型均难以准确预测竖直分层颗粒堆积床Bed-9的两相流动阻力压降。特别是在较高流速下,竖直分层颗粒堆积床的两相流动阻力压降不仅远高于相同大尺寸颗粒的均匀堆积床,而且高于所有模型的计算值,因此迫切需要针对分层结构颗粒堆积床内的流动阻力特性开展进一步研究。
4 结 论
为了进一步研究具有分层结构的颗粒堆积床内的流动阻力特性,本文使用4种尺寸球形颗粒分别构建了颗粒均匀堆积床、水平分层颗粒堆积床和竖直分层颗粒堆积床,开展了单相/两相流动实验,并对比分析了不同堆积结构颗粒床内的流动阻力特性,研究结果如下。
(1)对水平分层颗粒堆积床,当小颗粒在下层、大颗粒在上层时,分层结构对颗粒床内各部分的流动阻力影响较小。对小颗粒在上层、大颗粒在下层的水平分层堆积结构,分层结构对下层流动压降的影响较小,但会显著增加上层小颗粒堆积床内的流动阻力。在最大的实验流速工况下,上层小颗粒堆积床的流动阻力是小颗粒均匀堆积床的1.25倍。
(2)分析认为竖直分层颗粒堆积床内存在水平和竖直两个方向的多维流动现象,导致竖直分层颗粒堆积床的两相流动阻力压降低于小尺寸颗粒均匀堆积床,但高于大尺寸颗粒均匀堆积床。
(3)目前已开发出的颗粒堆积床流动阻力预测模型均无法对分层堆积结构的流动阻力压降进行预测,需要开展进一步研究。
