四面体构架式可展天线型面划分与程序化建模

2019-07-11许允斗郭路瑶姚建涛赵永生

中国机械工程 2019年12期

韩博许允斗,2 郭路瑶张硕姚建涛,2 赵永生,2

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

0 引言

随着航天事业的不断发展，空间可展机构在深空探测、卫星通信以及军事侦查等领域得到了广泛应用[1]。空间可展机构在航天领域的一个重要应用是作为大口径空间可展天线的支撑机构。大口径空间可展天线多采用网状反射面与桁架式支撑背架相结合的形式，具有收拢率高、质量小的特点，目前在轨运行的空间可展天线主要有四面体构架式可展天线、周边桁架式可展天线，以及径向肋式可展天线等[2-6]。

四面体构架式可展天线由若干个相似的可展单元组成，具有较大的折叠比和较高的结构刚度，其型面精度也易于控制，已经在国内外获得了多次在轨应用，如中国的HJ-1-C卫星SAR天线和俄罗斯“联盟号”飞船、“和平号”空间站[7-9]。四面体构架式可展天线主要包括支撑桁架和金属反射网，金属网反射面固定于支撑机构上，通过支撑机构将其张成若干拼合的小平面[10]。小平面主要是三角形、四边形和六边形的，而3个节点可以确定一个平面单元，且三角形网格的结构具有较好的稳定性，可以提高结构刚度以及承受非对称载荷的能力，因此三角形网格在可展天线中应用较多[11]。

已有学者对天线的型面划分方式进行了深入研究，形成了不同的型面划分方法。AGRAWAL等[12]以平面单元逼近抛物面为目标，研究了天线反射面型面精度与平面单元尺寸之间的关系，给出了旋转抛物面天线型面精度与三角形平面单元边长之间的解析表达式。张京街等[13]将抛物面与三角形平面的关系转换为数学问题，通过牛顿迭代法求解方程组，最终得到三角形节点的空间位置。李团结等[14]针对环形桁架式索网天线的索网型面划分，提出了弧长划分和垂直投影划分相结合的方法。YANG等[15]根据穹顶结构中常用的三向网格法，提出了一种划分抛物面索网的改进三向网格方法，并给出了口径面上正三角形单元边长与实际反射面和期望反射面之间系统偏差的解析表达式。DENG等[16]则以环形桁架为依托，提出了一种适用于环形桁架可展天线的测地线网格的方法。田大可等[17]以六边形可展模块为分析对象，提出了将支撑桁架模块分为等尺寸、不等尺寸两种类型的六边形型面划分方法。以上方法均可实现抛物面天线型面的网格划分，但是划分过程均较为复杂。

在机构的程序化建模方面，陈雨等[18]研究了变速箱的参数化设计问题，基于VC编程语言对Pro/E 5.0软件进行了二次开发，开发了相应的工具包来方便快捷地设计出需要的变速箱；郭旭伟等[19]研究了虚拟环境下Stewart型并联机床的参数化建模问题，实现了工作空间计算的参数化和三维仿真；俞高红等[20]基于MATLAB和VB.NET混合编程技术，研究了齿轮分插机构的三维参数化设计问题；赵振宙等[21]、刘博林等[22]分别研究了风力涡流发生器和一种冲压驱动桥壳的参数化建模方法；葛晓波等[23]基于框架模型，提出了一种通过脚本对产品建模规则进行描述的语义模型，以及一种产品整机参数化建模的方法；关富玲等[24]研究了可展天线结构设计的程序实现问题；夏鸿建等[25]提出了一种工程约束推理求解和模型元素更新机制相结合的参数化方法。虽然科研人员对不同机构的程序化建模方法进行了探索，但是对大口径空间可展天线的程序化设计建模的研究较少。四面体构架式可展天线由多个四面体可展单元连接组成，不同尺寸的构件较多，手工建模较为复杂，亟需研究其程序化建模方法。

本文针对四面体构架式可展天线进行研究，分析了其机构构型及机构单元组网方式，提取出了基本组合单元机构，提出了一种较为简单的包含中心节点的六边形型面划分方法。基于MATLAB和SOLIDWORKS提出了一种程序化建模的方法，采用VBA编程语言对SOLIDWORKS进行二次开发，编制了插件，并通过两个实例验证了所提出的型面划分方法以及程序化建模方法的正确性。

1 四面体构架式可展天线机构构型

四面体构架式可展天线整体如图1所示，其支撑机构是由多个四面体可展机构单元，通过共用节点花盘或连杆组合而成的。支撑机构的型面包括反射面和支撑面。支撑面用来提升整体机构的刚度，整体天线依靠支撑机构反射面(多为抛物面)上铺设的金属反射网进行信号的接收与传递。

图1 四面体构架式可展天线Fig.1 Tetrahedral truss deployable antenna

根据抛物面位置的不同，四面体构架式可展天线可分为正馈式和偏馈式，如图2所示，其主要差别如下：正馈形式天线的圆柱切面的旋转轴线与抛物面的旋转轴线重合，偏馈形式天线的圆柱切面的旋转轴线与抛物面的旋转轴线有一定偏距。抛物面的外轮廓为椭球面，正馈式和偏馈式的四面体构架式可展天线在结构上并无较大不同，仅在天线型面形状上有所不同。

图2 四面体构架式可展天线分类Fig.2 Classification of tetrahedral truss deployable antennas

如图3所示，四面体可展机构单元包括节点O、A、B、C及连接节点的6根杆件，其中，底部节点间的连接杆件称为同步杆，底部节点与顶部节点之间的连接杆件称为腹杆。四面体可展机构单元通过节点间连接杆件的折叠运动实现机构的收展。

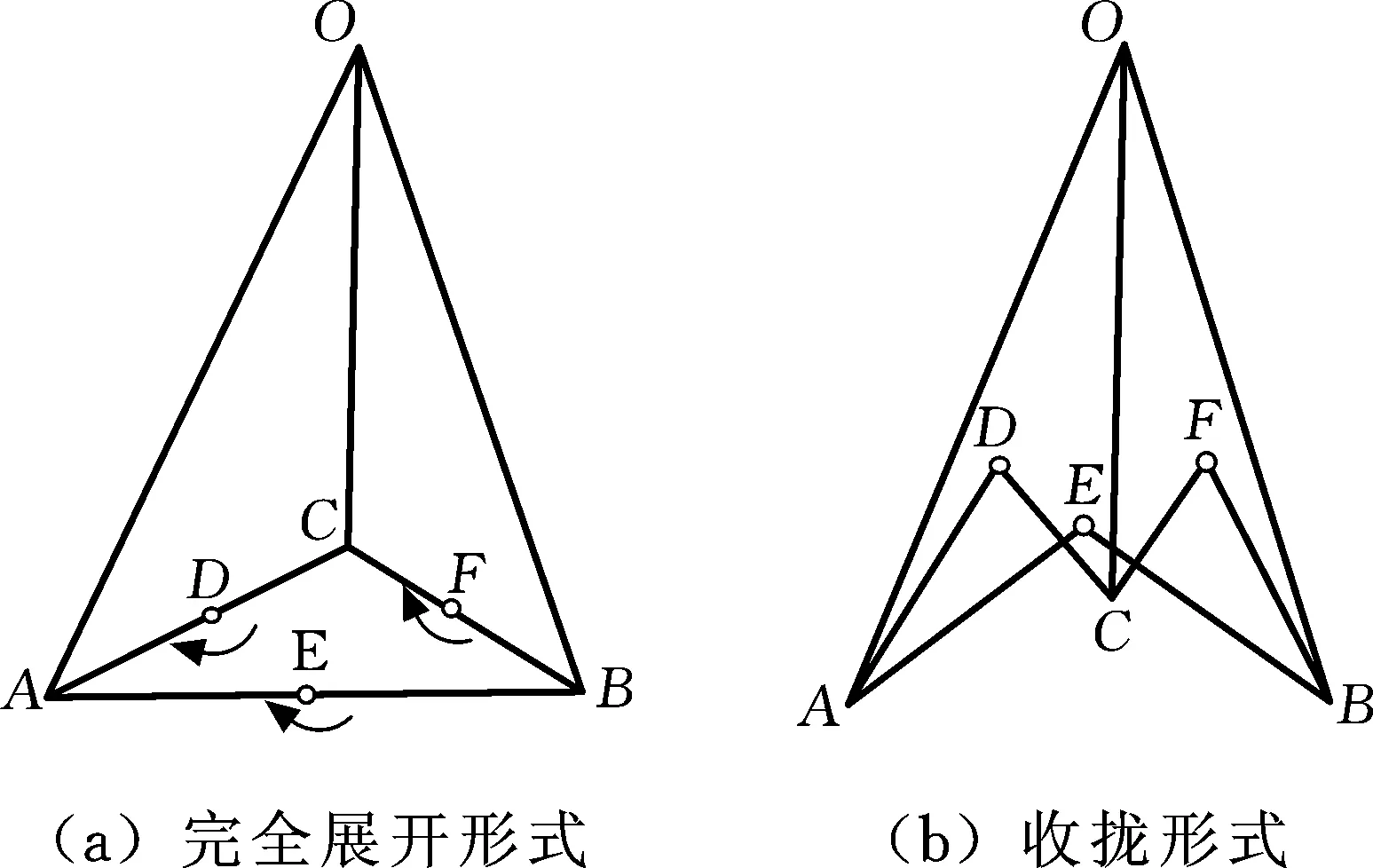
图3 四面体可展机构单元Fig.3 Tetrahedral deployable mechanism unit

四面体可展机构单元组网时，通过反射面节点花盘所在的三角形平面组合来逼近旋转抛物面，为减轻机构复杂程度，同时减小天线整体质量，四面体可展机构单元在可展天线抛物面上采用间隔式分布，如图4a所示。为了增加整体桁架机构的刚度，在四面体可展机构单元的顶部节点花盘之间需要添加相应的连接支链，如图4b所示。

图4 四面体可展机构单元组Fig.4 Group of tetrahedral deployable mechanisms units

由图4b可以发现，在四面体可展机构单元的顶部节点花盘之间添加相应的连接支链后，顶花盘连接支链也组合成了多个三角形网格单元，且顶部的3个顶花盘连接形成的三角形平面也为间隔式分布。对于有腹杆连接的单元，3个四面体可展机构单元的顶花盘(位于支撑面上)和3个单元共用的底花盘(位于反射面上)共同组成了一个倒置的四面体可展机构单元。对组网后的四面体构架式可展天线机构进行模块划分，可以得到其四面体可展机构的基本组合单元，如图5所示，整个天线机构由多个基本组合单元连接组成。

图5 基本组合单元机构Fig.5 Basic combination units mechanism

2 四面体构架式可展天线型面划分

通过天线反射面的型面划分可以确定实际反射面型面中各节点的合理位置，是索网天线结构设计的首要任务。现有的天线型面划分方法适用于包括四面体可展机构单元的各种型面的组网方式，但计算过程较为复杂。对于四面体构架式可展天线的三角形网格型面，由于位于型面中心位置处的基本组合单元机构具有旋转对称性，因此连接反射面上7个花盘的中心将形成正六棱锥，如图6所示，其中，QA=QB=QC=QD=QE=QF，对于天线型面上其他位置的基本组合单元，则具有棱边两两相等的特点。基于四面体构架式可展天线型面的中心六边形棱边均相等，其他位置六边形棱边两两相等这一特征，这里提出一种较为简单的包含中心节点的六边形型面划分方法。

图6 六棱锥示意图Fig.6 Schematic diagram of hexagonal pyramid

采用包含中心节点的六边形型面划分方法对四面体构架式可展天线机构进行型面划分时，首先得到抛物面上六边形模块的拓扑规律，在天线的口径面上划分出正六边形的组合，如图7所示；然后绘制出每个六边形单元的中心，各个六边形单元的中心相连后，呈现出三角形分布的规律，设定六边形边长为lA，三角形边长为lB。

图7 天线口径面上的六边形分布规律Fig.7 Hexagon distribution on antenna aperture surface

包含中心节点的六边形型面划分方法的具体步骤如下。

(1)给定型面误差δrms，按照下式[13]：

(1)

式中，f为天线型面焦距。

(2)依照口径面的直径D和三角形边长得到细分数N，N为大于D/lB的最小整数，进而通过N进一步获得圆整后的三角形边长l′B。

(3)将口径面的内接正六边形划分为多个边长为l′B的正三角形，三角形顶点的位置为对应的正六边形的中心位置，利用坐标变换得到各个正六边形的节点坐标。

(4)将口径面上的正六边形沿抛物面的旋转轴方向映射至旋转抛物面。

(5)根据抛物面上的六边形单元确定基本模块中心节点的位置，进而利用坐标变换得到所有节点的坐标，从而完成整个抛物面的型面划分。

对于正六边形，依据旋转变换矩阵很容易得到其中心节点和6个顶点之间的变换关系，如图8所示，设定六边形的边长为l′A，则依据坐标变换很容易得到节点P1～P6的坐标。

图8 六边形顶点的分布Fig.8 Distribution of hexagon vertices

依据几何关系首先得到点P1的坐标：

p1=(l′Acos30°,l′Asin30°,0)

(2)

依据坐标变换得到其余点的坐标：

pi+1=l′A(cos(φi+30°),sin(φi-30°),0)
φi=i×60°i=1,2,…,5

(3)

得到平面上六边形单元的分布规律之后，由于给定抛物面上的六边形是平面六边形单元沿旋转轴投影得到的，因而按照抛物面的方程可以容易得到抛物面上对应点的坐标，如图9所示。

图9 口径面网格单元向抛物面投影Fig.9 Projection of mesh units of aperture surface to paraboloid

平面上的任意一点K的坐标为(x,y,0)，假设抛物面方程为

x2+y2=nfz

(4)

式中，n为正整数。

点K向抛物面投影映射后，对应于抛物面上的点K1，其坐标为(x1,y1,z1)，两点的坐标满足如下关系：

(5)

天线口径面上的六边形中心点Q向抛物面映射后的坐标可通过如下方式获得。设Q在抛物面上对应节点Q1的坐标为(xQ1,yQ1,zQ1)，中心点Q1所在基本组合单元的顶点在抛物面上的投影点P1j的坐标为(xP1，j,yP1，j,zP1，j),j=1,2,…,6，则各坐标量满足如下的关系：

(6)

k=1,3,5

由于抛物面上的6个顶点P1j同属于一个基本组合单元，所以它们在天线口径面上的投影为正六边形，因而其坐标值均满足式(3)。

基于以上分析得到了满足映射规律的抛物面六边形划分方法，以六边形单元为基本组合单元，利用其中心点及各个顶点的分布规律进行坐标运算，得到各个节点坐标，连接各个节点可以得到三角形网格划分后的天线型面。这种天线网格划分方法过程简单直观，且是以中心对称六棱锥为基础进行网格划分的，划分后的三角形网格的杆件长度一致性较好，整体网格质量较高。

3 四面体构架式可展天线程序化建模

四面体构架式可展天线机构所含四面体单元较多，且各个四面体单元机构连接组合后需要使天线反射面为抛物面，这会导致不同四面体单元机构中的构件尺寸不同，设计者手工建模的工作量较大、设计周期较长、修改较为繁琐，应用程序化设计可以大大缩短设计者的建模时间，提升工作效率，同时模型易于修改，可有效提高设计质量。

3.1 传统手动建模关键步骤

四面体构架式可展天线机构设计步骤较为复杂，手动建模的关键步骤(图10)如下：

图10 建模关键步骤Fig.10 Key steps of modeling

(1)设定天线口径与抛物面型面曲率、焦距等关键参数，采用型面网格划分方法进行型面划分，得到天线反射面上各个节点的空间位置，在建模软件中输入坐标绘制反射面上的各个节点；

(2)设定四面体可展机构单元腹杆的杆长，利用反射面各三角形网格节点，计算得出各个支撑面节点的空间位置，在建模软件中输入坐标绘制支撑面上的各个节点；

(3)连接四面体构架式可展天线反射面及支撑面的各个节点，形成整体线框模型；

(5)在确定的位形下，对整体模型中的节点花盘、同步杆及腹杆进行结构设计。

在四面体构架式可展天线机构的设计阶段，需要对整体机构进行运动仿真，并对杆件及节点进行尺度优化，最后进行结构设计。运动仿真及尺度优化均通过天线的整体线框模型来实现，因此，这里主要研究四面体构架式可展天线机构整体线框模型的程序化建模。

3.2 程序化建模

程序化建模主要步骤与手动建模步骤相同，利用MATLAB的计算功能和SOLIDWORKS的绘图功能进行程序化建模，具体建模方法及过程如下。

3.2.1MATLAB软件计算与存储

设定四面体构架式可展天线口径与抛物面型面曲率、焦距等关键参数，采用包含中心节点的六边形型面划分方法，对四面体构架式可展天线进行型面划分，计算得到四面体构架式可展天线机构上各个节点坐标，用MATLAB编写的可视化操作界面如图11所示。

图11 可视化操作界面Fig.11 Visual operating interface

利用天线型面划分方法对天线型面进行划分，编制的MATLAB计算程序的主体程序代码较多，主要接口及赋值程序如下：

function pushbutton1_Callback (hObject,eventdata,handles)

说起酒，许多文人士大夫都和它结下了不解之缘。这其中就有浪漫主义诗人屈原“蕙肴烝兮兰藉，奠桂酒兮椒浆”，唐朝诗仙李白“人生得意须尽欢，莫使金樽空对月”，田园诗人陶渊明“欢言酌春酒，摘我园中疏”……但是，酒到了宋朝遇见苏东坡，擦出了不一样的火花。苏轼一生爱酒，但与许多文人不同，他爱酒却不溺酒。他虽一生仕途跌岩起伏，但不论顺境还是逆境，都淡泊从容。闲暇时亲自酿酒，率真豪放地约二三好友赴宴，饮酒赋诗。

shujudianlaiyuan(str2num(f),str2num(r1),str2num(N),str2num(L))

计算完成后，采用MATLAB中的xlswrite函数指令，将计算所得的各个节点坐标保存在Excel文件，供SOLIDWORKS调用，部分程序如下：

sheet=1;

xlswrite(filename,t,sheet);

采用以上命令即可将各个节点坐标存入到D盘目录下名为xkuang的Excel文件的表单1，其他数据文件亦可以按照此方法存入同一个Excel文件的不同表单。

3.2.2SOLIDWORKS软件程序化建模

在SOLIDWORKS中进行程序化建模时，需要针对SOLIDWORKS进行二次开发，通过SOLIDWORKS API接口，编制能够嵌入SOLIDWORKS的插件，通过调用插件进行程序化绘图。设计变量与编程结合的程序化建模方案如图12所示。

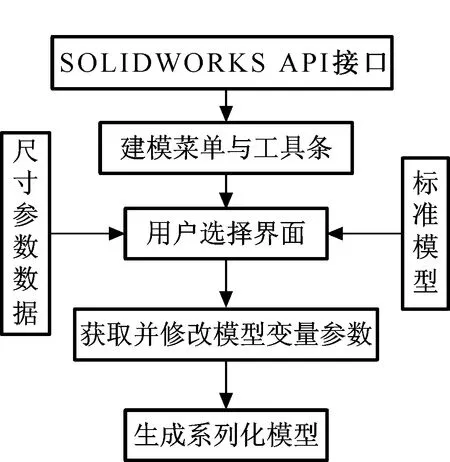
图12 程序化建模方案图Fig.12 Schematic diagram of programmatic modeling

具体开发步骤如下：

(1)通过SOLIDWORKS软件“工具”选项中“宏”模块中的“宏录制”命令，提取出手工绘图所用的操作指令的程序源代码，程序采用SOLIDWORKS自带的编程语言VBA(与语言VB兼容)；

(2)在SOLIDWORKS中，利用“新建宏”命令，建立能在SOLIDWORKS中打开的插件；

(3)在新建的插件中，采用VBA编程设计可视化界面；

(4)在新建的插件中，采用VBA调用MATLAB生成的数据文件表格，利用提取的绘图指令代码编写绘图程序；

(5)设定花盘尺寸，在新建的插件中，采用VBA通过每个四面体可展机构单元位于反射面上的3个节点建立基准面，并通过基准面的平移，建立支撑面花盘基准面；

(6)在新建的插件中，采用VBA在新建的基准面上编程绘制花盘和运动副的轴线，完成整体绘制。

典型指令操作程序VBA代码如下：

xlsApp.Workbooks.Open ("D: ianxian.xlsx")；

%导入Excel表格数据命令

xlsApp.Application.ActiveWorkbook.Sheets("Sheet1").Range("A" & CStr(i)).Value

%给点赋值命令

Part.SketchManager.CreatePoint(a,b,c)；

%生成坐标点命令

Part.SketchManager.CreateLine(Ax,Ay,Az,Bx,By,Bz)；

%利用两点绘制直线命令

SetmyRefPlane=Part.FeatureManager.InsertRefPlane(1,0,4,0,0,0)；

%建立基准面命令

4 型面划分与程序化建模验证

4.1 包含中心节点的六边形型面划分方法验证

采用包含中心节点的六边形型面划分方法对四面体构架式可展天线口径面进行网格划分，使用SOLIDWORKS绘制旋转抛物面，设定天线反射面截面抛物线的表达式为x2=8z，取天线口径面直径为4 m，六边形细分数N=4，按照步骤进行划分后，得到的结果如图13所示。使用包含中心节点的六边形划分方法对四面体构架式可展天线进行型面划分的过程较普通抛物面天线型面划分方法更为简洁直观，划分后的可展天线型面网格也较为均匀，天线反射面型面质量较好。