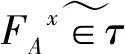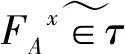软拓扑空间软连通分支的研究
2019-07-11马秋丽王小霞阮蒙蒙
马秋丽,王小霞,阮蒙蒙
(延安大学数学与计算机科学学院,陕西延安716000)
1999年Molodtsov D率先在文[1]中提出软集理论,从此,软集理论作为一个新兴的交叉研究方向,吸引了国际众多研究者的关注,文献[2-5]中引入软邻域、软闭包等等相关概念,文献[6]中定义了软子集,文献[7]中研究了软拓扑紧子空间的性质,文献[8]中研究了软拓扑空间中的分离性,给出了软T0,T1,T2,T3,T4空间定义及性质,文献[9]中给出了软T5空间,完善了软拓扑空间的分离性的研究,文献[10]中探究了软拓扑空间的连通性。本文在软拓扑空间的连通性的基础上,定义了软连通分支,给出了软拓扑空间(U,τ,E)中软连通分支的等价刻画,进一步研究了软连通分支的性质。
1 预备知识
定义1.1[1]如果F是从A→(U)的映射,则称(F,A)为论域U上的软集,论域U上的全体软集构成的集族,记作SSE(U)。
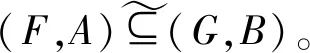
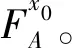
定义1.4[10]τ是论域U上带有固定参数集E的软集族,如果
(1)ØE,UE属于τ;
(2)在τ中的任意软集的并仍属于τ;
(3)在τ中有限软集的交仍属于τ。
则τ称为U上的软拓扑,记作(U,τ,E),(U,τ,E)中所有的元素都是软开集。

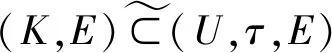
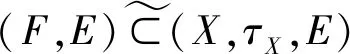
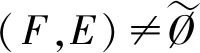
2 主要结果
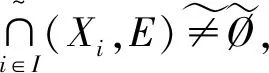
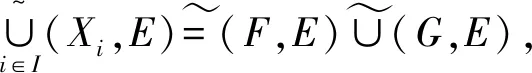

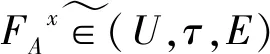
由以上定义可知,软点FAx,FAy和FAz同时在(X,τ,E)中,则有
(1)FAx和FAx软连通;
(2)如果FAx和FAy软连通,则FAy和FAx也是连软通的;
(3)如果FAx和FAy软连通,且FAz和FAx也是软连通的,则有FAx和FAz是软连通的。
由以上的定义可以得到,软点的软连通关系是等价关系。
定义2.2 将软拓扑空间(U,τ,E)中软点的软连通的等价类称为(U,τ,E)的软连通分支。
定理2.2 设(U,τ,E)是软拓扑空间,如果(X,τ,E)是(U,τ,E)上的软连通分支,则有

(2)(X,τ,E)是一个软连通子集;
(3)(X,τ,E)是一个软闭集。

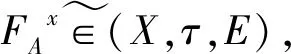
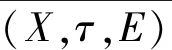


定理2.4 设(U,τ,E)是软拓扑空间,若(U,τ,E)中只存在有限个软连通分支,则(U,τ,E)中的任意的软连通分支都是软拓扑空间(U,τ,E)中的既软开又软闭的。