一种高动态低信噪比卫星导航信号捕获方法
2019-07-11王腾
王 腾
(北京自动化控制设备研究所,北京 100074)
0 引言
在室内、隧道、密林等具有遮挡的应用环境中,卫星导航信号的信号强度通常非常微弱[1]。为了在低信噪比的情况下捕获到卫星导航信号,接收机可以进行长时间的相干积分来提高信号处理增益及捕获概率,采用辅助全球卫星定位系统(Assisted Global Positioning System,AGPS)方案的接收机甚至能够消除数据比特跳变的影响而将相干积分时间延长至数百毫秒[2]。然而,在高动态、低信噪比的环境下,信号的多普勒频率变化率会导致本地样本信号与输入信号在长积分时间内出现较大的频率误差,相干积分处理增益受到大幅衰减[3]。非相干积累对频率偏差不敏感,但是累加过程中存在严重的平方损耗[4],增加非相干积分时间所获得的积分增益很有限。因此,传统的时、频域捕获算法的捕获灵敏度和动态性能通常是矛盾的。
与传统傅里叶变换相比,分数阶傅里叶变换(Fractional Fourier Transform, FrFT)增加了一个调频率参数,具有更高的自由度并且更适用于处理线性调频信号[7]。而带有多普勒频率变化率的卫星导航信号则是一种典型的线性调频信号,利用FrFT来处理高动态卫星导航信号有望解决捕获灵敏度和动态性能之间的矛盾。例如,Fan等利用了离散chirp傅立叶变换来估计接收信号的多普勒频率以及频率变化率,但是当频率变化率较大时估计误差很大[5]。Xia等则给出了一种FrFT的方法来处理高动态卫星导航信号,但并没有就微弱信号的捕获性能进行分析[6]。此外,FrFT还存在与快速傅里叶变换(Fast Fourier Transform,FFT)计算复杂度相近的离散计算方法,便于工程应用[8]。因此,有必要研究基于FrFT的高动态、低信噪比卫星导航信号捕获方法。
本文提出了一种基于FrFT和部分匹配滤波(Partial Matched Filter,PMF)的快速捕获算法。算法首先利用PMF对接收信号进行分段积分,随后借助FFT对分段积分结果做离散快速FrFT。由于具有多普勒频率变化率的卫星导航信号能够在分数域呈现能量聚焦,所提算法可以获得比传统PMF-FFT算法[8]更高的处理增益,因此捕获概率以及捕获灵敏度均能得到改善。最后,本文对所提算法的计算复杂度、捕获时间以及捕获概率进行了理论分析和仿真验证,并与传统的PMF-FFT方法进行了对比。
1 信号模型
以GPS L1频点的中频信号为例,考虑包含多普勒频率以及多普勒频率变化率的动态场景,那么接收机收到的中频复信号可以表示为
s(t)=D(t-τ)C(t-τ)ej2π(fi+f0)t+jπfat2+n(t)
(1)
其中,D(t-τ)为数据编码,C(t-τ)为扩频码,τ为传播时延,fi为中频频率,f0为多普勒起始频率,fa为多普勒频率变化率,也称调频率。对式(1)做分段相干积分后的复信号输出可以表示为
(2)
其中,R为码自相关函数,Δτ为码相位延迟误差,ts为采样时间间隔,Δf0为样本信号和接收信号间的初始频移误差,Nc为分段相干积分长度,N(n)为零均值复高斯白噪声,n表示第n段分段相干积分。
假设θ(t)2πΔf0t+πfat2,且多普勒频率变化率fa在整个积分区间0到Nctsn内保持不变,那么积分区间内的平均角速度可以表示为
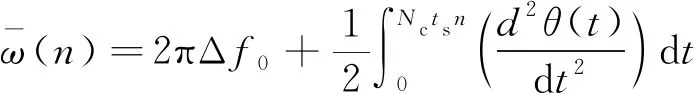
(3)
相应地,式(2)可以变为
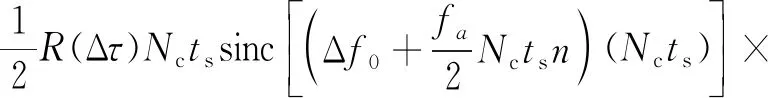
(4)
由式(4)可以看到,频率误差会导致积分输出带有衰减因子sinc[(Δf0+Nctsn/2)(Ncts)]。当接收信号存在多普勒频率变化率fa时,延长相干积分时间会导致频率误差Δf0不断增大,并使得积分增益不断降低。由文献[2]可知,当频偏超过0.44/Ncts时,功率衰减会超过3dB。
2 PMF-FrFT捕获算法及性能分析
2.1 PMF-FrFT捕获算法
由文献[7]可知,信号x(t)的FrFT可以表述为
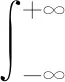
(5)
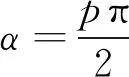
对调频率为fa的线性调频信号做角度为α=arccot(2πfa)的FrFT之后,原始的(t,ω)时频平面将转换至分数域平面(u,v),信号功率将会在该平面聚焦。通过检测聚焦峰值的位置,可以估计得到多普勒频率及多普勒频率变化率。
为了便于工程实现,文献[8]给出了一种分解型的FrFT快速计算方法并获得了广泛的应用,FrFT的离散形式可以表示为
(6)
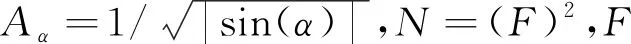
式(6)为信号的离散卷积形式,可以借助FFT来快速实现。但是由于F未必是整数,时域信号的2F倍内插在卫星定位接收机中难以实现。为此,本文采用2倍内插来代替2F倍内插。如图1所示,PMF-FrFT算法的具体实现方式如下。
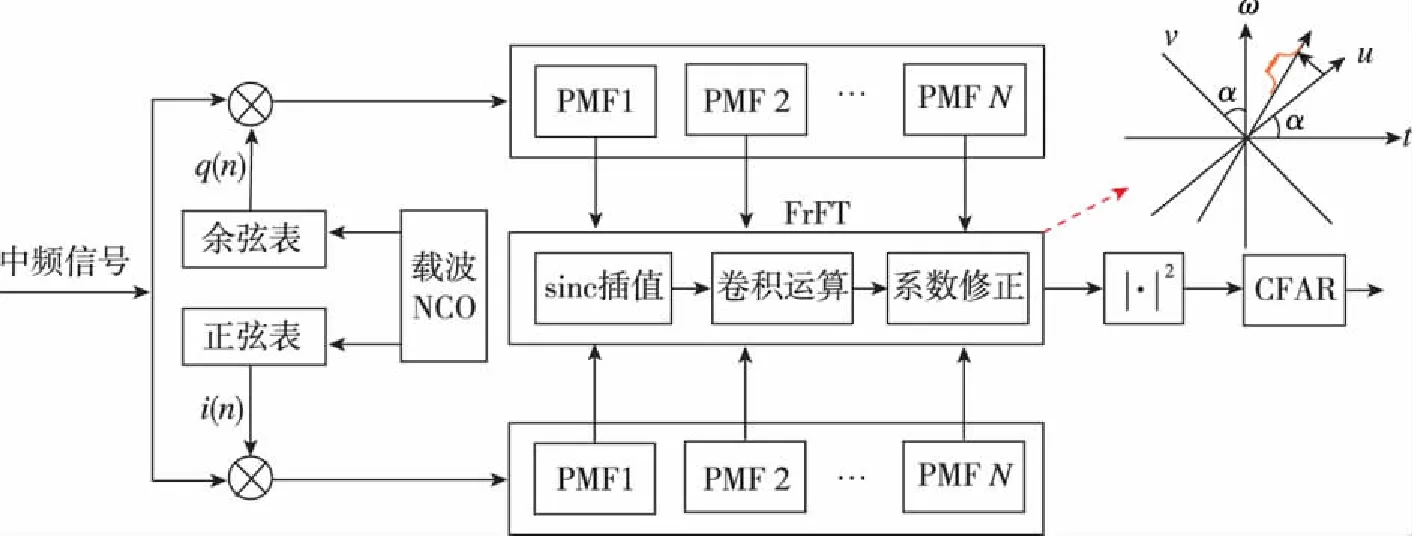
图1 所提PMF-FrFT算法流程图Fig.1 The diagram of the proposed PMF-FrFT algorithm
步骤1:采用PMF法对中频接收信号进行总长度为NNcts的相干积分,每段相干积分长度为Ncts,相干积分输出结果如式(4)所示;
步骤2:利用FFT对式(4)的结果S(n)做2倍sinc插值,具体操作如式(7)所示
(7)
其中,S(n/2)表示2倍sinc插值,S0(n/2)表示2倍补零内插,FFT(·)、IFFT(·)分别表示快速傅里叶变换以及逆快速傅里叶变换。
步骤3:利用FFT实现式(6)中的卷积运算
(8)
步骤4:修正系数,完成离散快速FrFT运算
(9)
步骤5:以Δfa为调频率搜索步长在区间[fl,fu]内重复步骤2~4,比较公式的输出峰值,根据输出最大峰值的位置以及相应的变换阶次得到多普勒频率变化率和多普勒频率偏差的估计值[9],完成信号的捕获。其中fu为阶次搜索范围的上界,fl则为下界
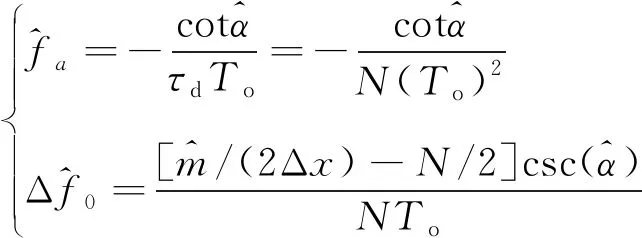
(10)
2.2 性能分析
2.2.1 计算复杂度
PMF-FrFT算法与传统PMF-FFT算法运算量的不同主要体现在FrFT运算上。由于2N点的FFT所需复乘次数为2Nlog2(2N)[11],而步骤2、3均通过3次2N点FFT运算来实现,那么步骤2~4共需复乘次数ο=6×(2N)log(2N)+8N。此外,PMF-FrFT算法需要在调频率区间[fl,fu]内进行搜索,除去运算量相同的PMF部分,PMF-FrFT算法的计算量是传统PMF-FFT的6|fu-fl|/Δfa以上,呈线性增长关系。在实际应用中,可以借助载体运动的先验信息或者诸如文献[10]和文献[15]中的搜索方法来缩小调频率搜索区间,减少所提算法的计算量。
2.2.2 虚警概率及检测概率
虚警概率是由进入检测模块中噪声的分布与其预置门限的关系决定的。当信号不存在时,送入恒虚警检测器的FrFT输出结果服从自由度为4的中心χ2分布[12],假设判决门限为η,那么将其中一点输出结果送入门限检测器中的虚警概率为
由于FrFT的输出结果具有相同的概率分布,当采用最大值判决的MAX准则时,虚警情形等于所有判决量均不虚警情形的补集[13],即总虚警概率为
(11)
而当信号存在时,观测量服从自由度为4的非中心χ2分布[12],将其中一点输出结果送入门限检测器中的捕获概率可表示为
(12)
其中,Q2(·,·)为广义Marcum Q函数,I1(·)为一阶修正贝塞尔函数。由于虚警概率较低,假设检测过程中不发生虚警,而任意点都有可能捕获到信号,因此最终的检测概率可以表示为
(13)
由式(11)可以看到,由于要在多个分数域进行搜索检测,因此在检测门限相同的情况下,搜索次数越多虚警概率则越大,在实际应用过程中应尽量缩小阶次搜索范围,同时适当提高检测门限;而从式(12)和式(13)可以看出,所提算法的检测概率仅和检测门限以及检测信噪比有关,这和传统PMF-FFT算法是一致的,即使检测门限因虚警概率而有所提高,所提算法仍然可以通过延长相干积分时间来提高检测信噪比,进而提高检测概率。
2.2.3 平均捕获时间
文献[14]给出了传统PMF-FFT的捕获时间,类似地,PMF-FrFT的平均捕获时间可以表示为
(14)
其中,PFA表示虚警概率,Kp为校验惩罚因子,q为码相位搜索单元,Pd,a为信号加速度为α时的检测概率,Tfrft为一次FrFT所需的时间。在工程应用中,采用现场可编程门阵列(Field Programmable Gate Array, FPGA)进行FFT运算所需的时间可低至微秒级[17],那么本文所提的FrFT快速实现算法所需的运算时间也能控制在微秒级。只要在合理的区间内进行调频率搜索,平均捕获时间并不会因此而大幅增加。相反,在低信噪比的环境下,由于通过长时间相干积分提高了捕获概率,平均捕获时间与无法采用长时间相干积分的PMF-FFT算法相比反而有可能会大幅度降低。
3 仿真分析
本节利用蒙特卡罗仿真对所提PMF-FrFT算法的捕获概率和捕获时间进行了验证分析。为了突出所提算法的优势,仿真以AGPS高精度接收机接收GPS L1频点信号为例,因此忽略了比特翻转对于相干积分时间的限制。初始频率偏差为0Hz,分段匹配滤波的长度为1ms,调频率搜索步长根据相干积分对于频率偏差的容忍度设为5Hz/s,动态性能考虑10g和25g两种情况。此外,仿真也给出了传统PMF-FFT算法的捕获性能用于对比分析。仿真参数设置如表1所示。
首先对所提算法的捕获性能进行仿真分析。图2给出了PMF-FrFT算法在不同虚警概率下的捕获概率仿真曲线和式(13)理论曲线的对比。从图2中可以看出,仿真曲线与理论曲线十分接近,因此可以证明式(13)的正确性。仿真曲线比理论曲线稍差是因为FrFT对多普勒频率变化率的估计精度是有限的,无法保证信号能量完全聚焦。
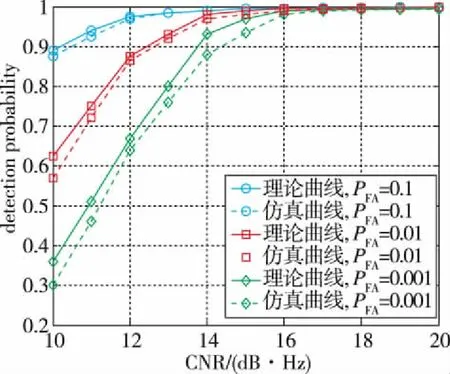
图2 不同虚警概率下PMF-FrFT的检测性能,加速度25gFig.2 Detection probability curves of the PMF-FrFT for different false alarm probabilities, with the acceleration of 25g
图3分别给出了不同动态、不同相干积分时间条件下PMF-FrFT与PMF-FFT算法的捕获概率曲线。由文献[2]可知,当加速度为10g时,PMF-FFT算法的最优相干积分时间为26ms,25g时则缩短至16ms。如图3所示,由于频率变化率的存在,频率偏差随着相干积分时间的增加而不断增大,在超过最优相干积分时间之后继续延长相干积分时间反而会降低捕获概率。当加速度为10g、相干积分延长至60ms时,PMF-FFT将难以获得积分增益,捕获概率趋近于0;同样地,当加速度为25g、相干积分延长至40ms时,捕获概率将趋近于0。相反,由于不受频率变化率的影响,所提PMF-FrFT算法能够在相同载噪比和积分时间的条件下获得比PMF-FFT更高的捕获概率,并且可以通过不断延长相干积分时间来改善捕获灵敏度。如图3所示,当加速度为10g时,PMF-FrFT通过将积分时间延长至512ms来将捕获灵敏度从PMF-FFT的28dB·Hz降低至16dB·Hz;而当加速度为25g时,PMF-FrFT仍可采用512ms的相干积分将捕获灵敏度从PMF-FFT的30dB·Hz降低至16dB·Hz。
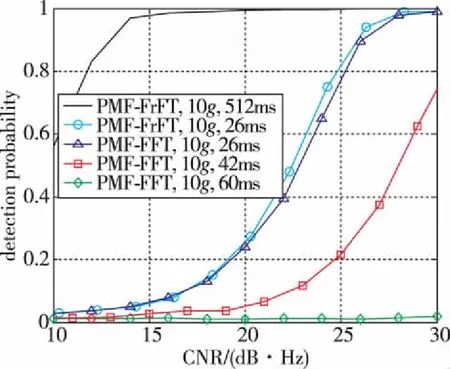
(a)加速度10g
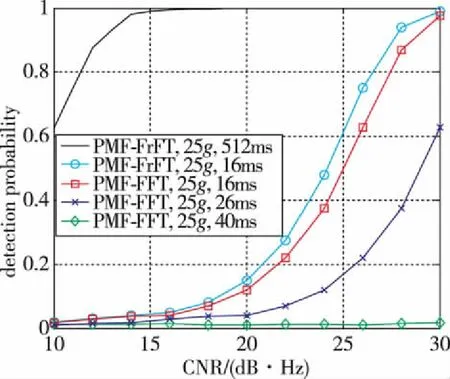
(b)加速度25g图3 PMF-FrFT与PMF-FFT的捕获概率对比, 虚警概率为0.01Fig.3 Detection probability comparions between PMF-FrFT and PMF-FFT, with the false alarm probability of 0.01
最后,对PMF-FrFT的捕获时间进行仿真分析。假设虚警概率为0.01,载体加速度为25g,码搜索单元为2046个,频率搜索区间为1个,调频率搜索区间为10g~25g,图4给出了所提算法与传统PMF-FFT算法的捕获时间仿真曲线,其中FrFT的运算时间采用文献[17]给出的880μs统计。如图4所示,尽管PMF-FrFT的相干积分时间为512ms,并且还需要进行调频率搜索,而PMF-FFT的相干积分时间不超过26ms,且仅需一次FFT。当载噪比低于21dB·Hz时,PMF-FrFT的捕获时间仍然低于PMF-FFT;当载噪比低于15dB·Hz时更是比PMF-FFT少了10倍以上。不过,随着载噪比的提升,PMF-FFT的平均捕获时间不断下降,但所提PMF-FrFT算法由于相干积分时间较长的原因,捕获时间并未随着载噪比的提升而下降。
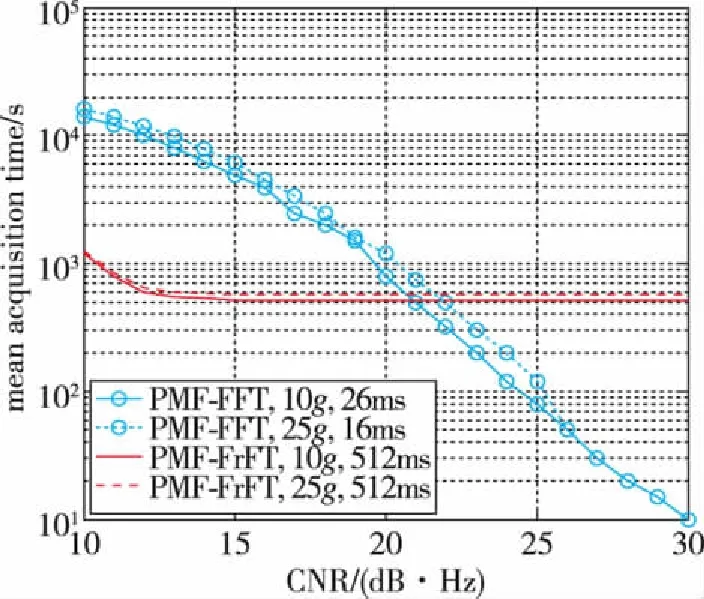
图4 PMF-FrFT与PMF-FFT的平均捕获 时间对比,虚警概率为0.01Fig.4 Mean acquisition time comparions between PMF-FrFT and PMF-FFT, false alarm probability is 0.01
4 结论
本文提出了一种基于PMF-FrFT的捕获算法,用于提升高动态、低信噪比环境下卫星导航信号的捕获性能。本文所做工作及所得结论如下:
1)建立了高动态卫星导航信号的数学模型,在此基础上提出了基于PMF-FrFT的捕获算法,算法可借助FFT来快速实现,具有工程应用价值。
2)对PMF-FrFT算法的捕获概率、捕获时间以及计算复杂度等性能指标进行了理论分析。分析表明,在高动态、低信噪比环境下PMF-FrFT算法能够通过延长相干积分时间的方法来提高捕获概率,降低平均捕获时间,算法计算量与传统PMF-FFT算法相比仅随调频率搜索空间的增加而线性增加。
3)利用蒙特卡罗仿真对所提算法的捕获性能进行了仿真验证,并和传统PMF-FFT算法进行了对比分析。仿真表明,所提PMF-FrFT算法在加速度为25g时,可以利用512ms的长时间相干积分将接收机捕获灵敏度由传统PMF-FFT的30dB·Hz降低至16dB·Hz,且捕获时间减少8倍以上。
