大型全悬挂舵几何要素值的选取

管庆祥，王海波，张 黎

（大连船舶重工集团设计研究院船研所，辽宁 大连 116005）

0 引 言

随着船舶逐渐朝高性能化方向发展，全悬挂舵的应用越来越广泛。船级社的规范和规则虽然对全悬挂舵的设计有一些指导和要求，但还需设计人员对其进行深入研究。全悬挂舵设计的难题之一是合理设计舵杆和舵套筒结构[1]，舵杆直径过大会导致舵叶厚度比过大，进而导致舵叶受到的阻力增大，使船舶的推进能效降低。对于大型全悬挂舵而言，为减小舵杆直径，仅依靠高强度锻钢材料是不够的，还必须把舵杆和舵套筒插入舵叶内部，减小舵杆在下舵套处承受的弯矩。对于主尺度确定的船舶而言，当船东对其操纵性的要求未超出国际海事组织（International Maritime Organization, IMO）标准的要求时，其所需的舵叶面积基本上是确定的。在固定舵叶面积的基础上需选取合适的几何要素，从而使全悬挂舵既满足高性能要求，又具有适宜的舵杆和舵套筒直径，进而降低船舶的运营成本。

1 几何要素定义

舵套筒插入舵叶内部的全悬挂舵结构简图见图1。由于在进行舵系受力分析时均可采用平均舵叶宽度的方法将梯形舵叶简化为矩形舵叶，因此本文直接采用矩形舵叶进行公式推导，从而降低计算的复杂度。全悬挂舵主要几何要素和力学参数分别见表1和表2。

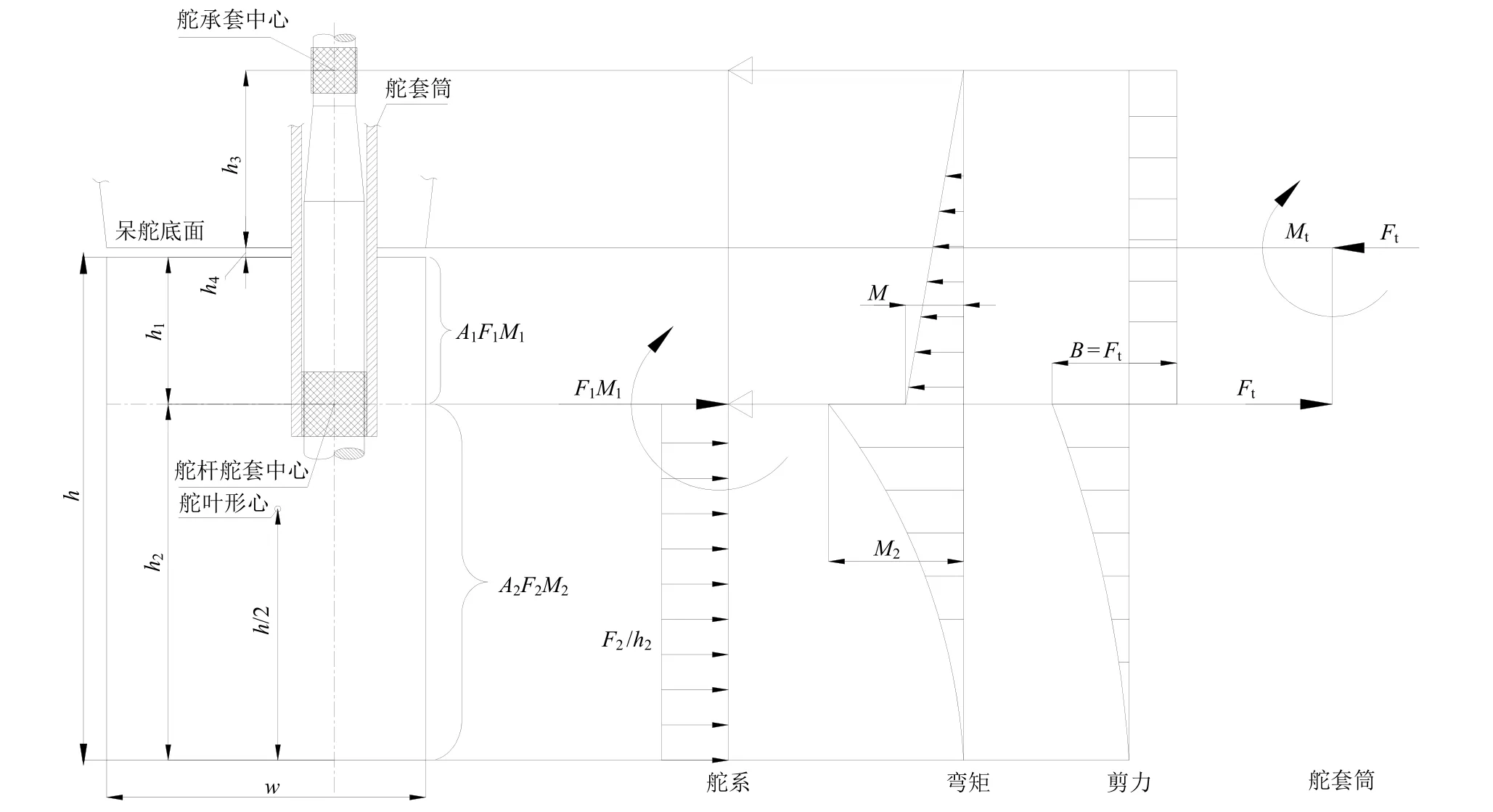
图1 舵套筒插入舵叶内部的全悬挂舵结构简图

表1 主要几何要素

表2 主要力学参数

受各种实船条件的限制，舵套筒插入深度比i的极限范围通常为0～0.5，展弦比λ的极限范围通常为1～2[2]。本文以该范围为例进行分析。

2 舵系力学分析

在各船级社规范中，普遍采用以下计算式进行舵系设计[3]。

1) 舵力F的计算式为

式(1)和式(2)中：λ为展弦比；k1为依据展弦比λ而定的系数；k2为舵叶剖面型线形状系数；k3为依据舵桨布置和舵叶处于螺旋桨尾流位置而选取的系数；A为舵叶面积；v为船舶最大服务航速。

2) 舵扭矩的计算式为

式(3)中：Q为舵扭矩；w为舵叶宽度。适用于平衡比为0.23～0.43的最大正车状态。考虑舵叶型线、舵叶结构设计和舵机规格等设计限制条件，大型全悬挂舵平衡比一般为0.3～0.4。

3) 下舵套处舵杆直径Dc的计算式为

式(3)中：k为材料系数；M为舵杆在下舵套中心处承受的弯矩。

对图1进行力学分析，以舵杆下舵套中点水平线为界，将舵叶分为上下2部分，各自的舵力和弯矩的计算式为

舵杆在下舵套中心处承受的弯矩为

舵套筒根部（即舵套筒与船体外板连接处）承受的剪切力和弯矩分别为

式(5)～式(11)中：F1为下舵套中心点以上的舵力；F2为下舵套中心点以下的舵力；h为舵叶高度；h1为下舵套中心点以上的舵叶高度；h2为下舵套中心点以下的舵叶高度；h3为上舵承套中心至呆舵底面的距离；h4为舵叶顶面至呆舵底面的距离；Ft为舵套筒与船体外板连接处承受的剪切力；M1为下舵套中心点以上的舵叶弯矩；M2为下舵套中心点以下的舵叶弯矩；Mt为舵套筒与船体外板连接处承受的弯矩。以上各参数可参见图1。

3 舵套筒插入舵叶深度比的关联影响

由舵力F和舵扭矩Q的计算式可知，当航速v、舵叶面积A、舵剖面型线形状系数k2和总体布置相关系数k3确定时，式中仅展弦比λ为变量，且其与舵套筒插入深度比i没有关联。

将式(5)～式(8)代入式(9)之后，舵杆弯矩计算式转换为

由式(12)可知，舵杆在下舵套中心处承受的弯矩为舵力乘以下舵套中心与舵叶中心的高度差。当舵叶主尺度确定之后，下舵套中心越接近舵叶中心，舵杆承受的弯矩越小。

引入舵套筒插入深度比i，舵杆承受的弯矩M的计算式转变为

由式(13)可知，舵杆承受的弯矩与舵套筒插入深度比呈线性单调递减关系。由式(4)可知，舵杆直径与舵杆弯矩呈单调递增关系，与舵套筒插入深度比呈单调递减关系。

通过引入展弦比λ计算i=0和i=0.5的舵杆直径比，得到

若展弦比λ的取值范围为 1～2，且该比值与展弦比λ呈单调递增关系，则该比值的取值范围为1.803～2.263，可见插入深度比和展弦比对舵杆直径的影响非常大。若几何要素选取不当，例如舵套筒插入深度不足、展弦比过大，会导致舵杆直径成倍增大。

舵套筒所承受的舵系剪切力和弯矩需满足剪切应力许可值、正应力许可值和综合应力许可值的要求。根据应力值反推舵套筒内外径与舵套筒插入深度比之间的函数关系比较复杂，可通过选定的舵系模型进行数值计算来推断二者之间的关系。

以一个矩形舵叶为例，固定舵套筒的外径为定值1000mm，内径为舵杆直径公式计算值加上100，通过使插入深度比i从0变化到0.5，计算出舵套筒的各应力值，绘制舵套筒应力与插入深度比的关系曲线和舵杆/舵套筒尺寸与插入深度比的关系曲线分别见图2和图3。

由图2和图3可知：当i＜0.2时，由于舵套筒壁厚的增加弱于舵套筒根部弯矩的增大，正应力变化剧烈；由于该范围内舵套筒的壁厚较薄，很难达到舵套安装所需的壁厚；由于舵杆直径很大，该舵叶厚度下的舵杆毂壁厚很薄，难以满足舵杆与舵杆毂过盈压装的要求。当i在0.2～0.4范围内时，应力值变化很小。反过来可理解为，当选取确定的应力值为设计点，舵套筒插入舵叶的位置在 0.2～0.4范围内变动时，舵套筒的内径随舵杆直径变化，舵套筒的外径可维持不变，进一步可理解为舵叶厚度比不用改变。当i＞0.4时，舵套筒插入深度较大，会对舵叶结构设计造成影响，且会导致舵杆毂和舵杆液压螺母均处于舵球的包络范围内，难以满足舵叶修理维护的要求。

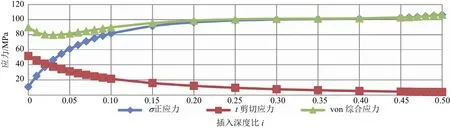
图2 舵套筒应力与插入深度比的关系曲线

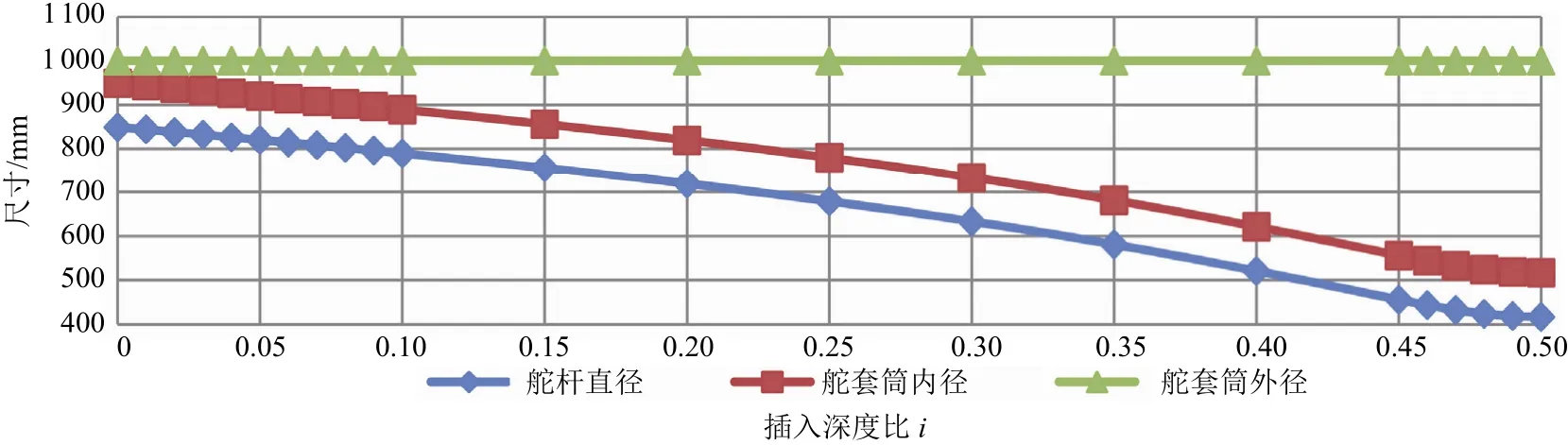
图3 舵杆/舵套筒尺寸与插入深度比的关系曲线

综上，推荐选择舵套筒插入深度比为0.30±0.05，这样既能得到合适的舵杆直径、舵套筒壁厚和舵杆毂壁厚，又能得到较小的舵叶厚度比，即较小的舵叶阻力。

4 展弦比的关联影响

以展弦比λ为变量，分别将其代入舵力、舵矩和舵杆直径计算式，得到

朱自清用多情的笔，生动地描绘了他的瑰丽人生。他生命虽然短暂，然而却留给人们一个缤纷而深邃的文学世界。品味他的散文，读者可以深切地领略他丰富微妙的情感生活，感悟他那温厚朴实又真挚无私的爱。他爱自然，爱家庭，爱朋友，爱祖国，在他的博爱天地中，一次次被其散文中优雅别致的情致美所折服和感动，这使得朱自清散文拥有了独特的情感魅力。

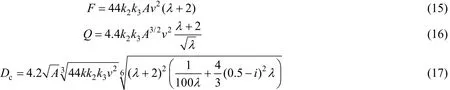
1) 当λ在1～2范围内时，舵力为展弦比的单调递增函数，F(2)/F(1)= 1.33。

2) 当λ在1～2范围内时，舵矩为展弦比的单调递减函数，Q(1)/Q(2)= 1.06，可见舵矩的变化范围较小，对与舵扭矩关系密切的舵系尺寸（如舵杆毂尺寸）设计的影响可忽略不计。

3) 当λ在1～2范围内时，由式(17)得出舵杆直径与展弦比的函数关系还与舵套筒插入深度比i有关，其函数性质完全由式(7)后半部分的六次根函数决定。该六次根函数可记为Dc-λi，相当于舵杆直径的舵叶几何要素系数。对Dc-λi进行函数分析，得到以下结论：

(1) 当i在0～0.461范围内时，舵杆直径为展弦比的单调递增函数；

(2) 当i在0.462～0.498范围内时，舵杆直径随展弦比先减小后增大；在i= 0.482时近似为对称函数；

Dc-λi舵杆直径系数关于展弦比λ的主要函数性质曲线见图4。根据插入深度比的论述，仅舵套筒插入深度比选择在0.2～0.4范围内时有实际设计意义，在该范围内舵杆直径与展弦比为单调递增关系，λ=2时的舵杆直径与λ=1时的舵杆直径的比值为

式(18)在i为0.2～0.4时为单调递减函数，直径比范围为1.223～1.158。可见，当舵套筒插入深度比相同时，瘦高的长方形舵叶相比正方形舵叶需配置更粗的舵杆。

综上可知，当推荐选取的舵套筒插入深度比在0.3±0.05范围内时，选择展弦比小的舵叶或直接选择正方形的舵叶可使舵杆直径更小，从而使舵叶总厚度较小。

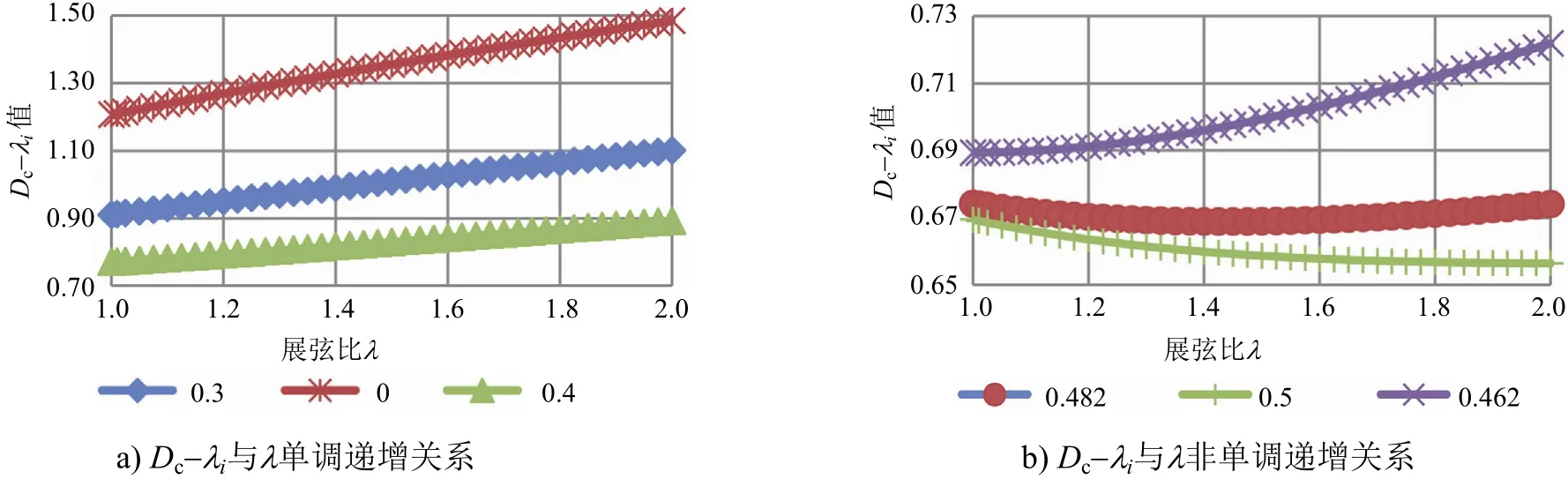
图4 Dc-λi舵杆直径系数关于展弦比λ的函数性质

5 结 语

大型高性能船舶的航速高，使用的全悬挂舵面积大，需选取最佳的舵叶几何要素，得到合适的舵杆和舵套筒尺寸以降低成本，得到较小的舵叶厚度比以降低舵叶阻力，从而提高船舶的推进效率。通过推导舵杆直径与舵套筒插入深度比和展弦比的数学表达式，结合舵套筒根部强度等设计要求，在同等舵系设计输入条件下，推荐选取舵套筒插入深度比为0.3±0.05，同时使展弦比接近于1，可得到较优的大型全悬挂舵系设计。

一般情况下，面积相同但展弦比小的舵叶舵效相对较小，因此建议采取改善舵叶剖面形状和加装制流板等措施对舵效进行弥补[4]。