基于理想变传动比的主动前轮转向滑模控制＊

李旭 史晓华 李瑞川 王建春 马勇,2

（1.山东科技大学，青岛 266590；2.山东海卓电液控制工程技术研究院，日照 276800）

主题词：主动前轮转向 理想变传动比 附加转角 滑模控制 转向性能

1 前言

主动前轮转向系统是介于电动助力转向和线控转向之间的转向系统[1]，可在一定范围内实现变传动比控制，对于提高车辆的操纵性、稳定性和轨迹保持能力具有重要的意义[2-3]。

目前，针对主动前轮转向的研究主要集中在可变传动比设计和车辆稳定性控制方面。针对可变传动比：Tajima J首先提出车辆的理想变传动比与稳态横摆角速度增益有关，为保证车辆具有良好的转向性能，稳态横摆角速度增益应该是不随车速变化的定值[4]；商高高设计了基于稳态横摆角速度增益的理想变传动比曲线[5]；周兵通过对比分析5种拟合变传动比曲线，证明改进型S函数与理想变传动比曲线具有最高的接近程度[6]。以上研究仅探究了主动前轮转向系统的传动比应遵循的规律，尚未提出具体的控制策略。

针对车辆稳定性控制，Nam K、桑楠等根据驾驶人驾驶意图和车辆的行驶状态分别利用H∞鲁棒控制、自抗扰控制等求解了主动前轮转向系统的附加转角[7-13]。这些研究通常假定主动前轮转向系统能够理想地产生所需要的附加转角，缺乏对该附加转角应遵循的理想传动比规律的研究[14-16]。

然而，基于理想变传动比的附加转角控制是决定主动前轮转向系统性能优劣的关键因素。王春燕提出一种理想传动比规律下的主动前轮附加转角闭环控制策略，但所采用的PID控制对于车辆行驶过程这一复杂时变、强非线性对象控制不佳。滑模控制响应迅速、鲁棒性好、物理实现简单，对非线性系统具有良好的控制效果，在响应速度、控制精度上均优于传统的PID控制。

基于此，本文提出一种基于理想变传动比规律的主动前轮转向滑模控制策略。以主动前轮转向系统为研究对象，建立七自由度车辆模型、Dugoff非线性轮胎模型；确定了固定横摆角速度增益下的理想变传动比规律。在此基础上，提出主动前轮转向附加转角的滑模控制策略，并在阶跃、蛇行转向工况下对其控制效果进行了仿真分析。

2 动力学模型

2.1 车辆动力学模型

考虑车辆纵向、侧向、横摆运动以及4个车轮的旋转运动，建立非线性七自由度整车模型如图1所示。

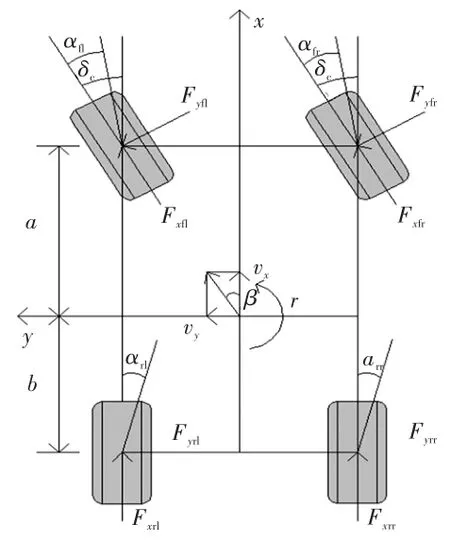
图1 七自由度整车模型

结合整车受力情况，根据牛顿第二定律可得车辆非线性动力学方程为：

式中，m为整车质量；vx、vy分别为纵向、横向车速；r为横摆角速度；Fxi、Fyi分别为轮胎纵向力、侧向力，i=fl,fr,rl,rr分别表示左前轮、右前轮、左后轮、右后轮；δc为前轮转角；Iz为整车绕z轴的转动惯量；a、b分别为前、后轴到质心的距离；tw1、tw2分别为前、后轴轮距；Itw为车轮的转动惯量；ωi为各车轮的角速度；R为车轮半径；Tbi为各车轮驱动力矩；Tdi为各车轮制动力矩。

2.2 轮胎模型

与魔术公式模型相比，Dugoff非线性模型允许各轮胎有独立的侧向刚度和纵向刚度，所需轮胎模型参数较少，可以较精确地拟合轮胎的稳态运动过程[17-19]，因此本文选用Dugoff轮胎模型。

设4个轮胎具有相同的纵向刚度，同轴的左、右侧轮胎具有相同的侧偏刚度，纵向力、侧向力计算公式为：

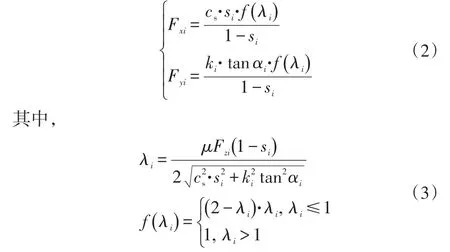
式中，cs为轮胎的纵向刚度；si为各轮胎的滑移率；ki为各轮胎的侧偏刚度；αi为各轮胎的侧偏角；Fzi为各轮胎的垂向载荷；μ为路面附着系数；λi为轮胎动态参数。

各轮胎垂向载荷、滑移率、侧偏角的计算公式，可由七自由度整车模型求得。

3 理想变传动比曲线的设计

3.1 稳态横摆角速度增益

线性二自由度汽车微分方程能够反映汽车曲线运动的最基本特征。等速行驶时，前轮角阶跃输入即可使车辆达到稳态即等速圆周行驶。此时=0，m=0，rm为稳态横摆角速度。线性二自由度微分方程为：

式中，k1、k2分别为前、后轮轮胎的侧偏刚度。

稳态横摆角速度增益为：

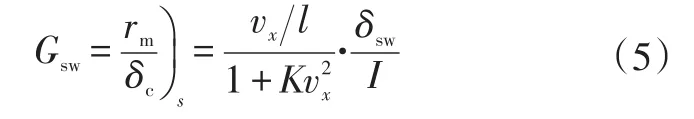
Tajima J提出，为保证转向盘转角和汽车航向角之间呈现出与车速无关的固定比例关系，稳态横摆角速度增益应为不随车速变化的定值，将基于固定横摆角速度增益确定的变传动比称为车辆的理想变传动比[4]。

德国汽车研究所通过试验得出[20]，轿车的稳态横摆角速度增益范围为0.16～0.33 s-1，本文选取Gsw=0.275 s-1。

3.2 理想变传动比规律

固定稳态横摆角速度增益下，传动比为：

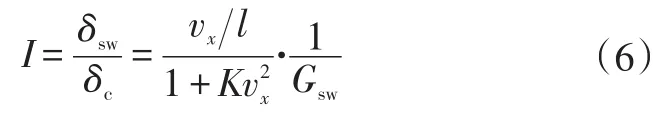
转向传动比过小，转向会过于灵敏，驾驶员微小的误操作会导致较大的车辆响应；反之则过于迟缓，不利于车辆的换道、避障。因此，变传动比曲线应有上、下界，下限Imin=fI(vx1)，上限Imax=fI(vx2)，其中vx1为下临界车速，vx2为上临界车速。

根据车辆仿真模型的基本参数（见表1），可确定理想变传动比曲线如图2所示，其规律为：

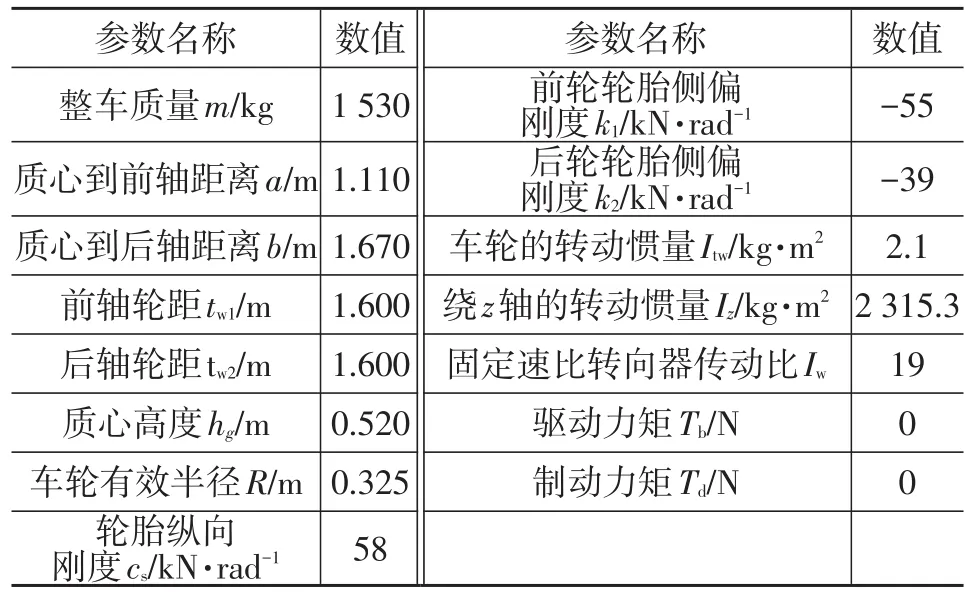
表1 主要仿真参数

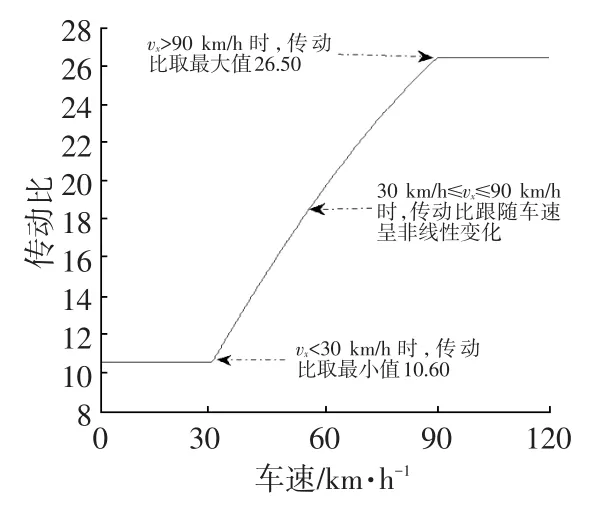
图2 理想变传动比曲线

4 基于理想变传动比的滑模控制策略

4.1 滑模控制策略

滑模控制策略通过将实际横摆角速度r与其理想值rd作对比，构建滑模面迫使实际横摆角速度跟随理想值的变化而变化。控制器的设计基于线性二自由度模型，理想传动比规律下，线性二自由度模型可用矩阵表示为：

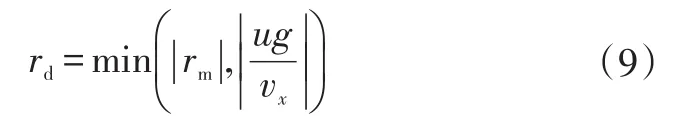
式中，g为重力加速度。

以七自由度整车模型的横摆角速度作为车辆的实际横摆角速度，二自由度汽车模型的横摆角速度作为理想横摆角速度，将两者之差作为控制误差，并以此构建滑模面s：

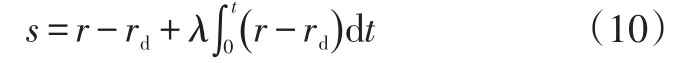
式中，λ为正加权系数。

令=0，可得前轮转角的等效输入量δfeq：

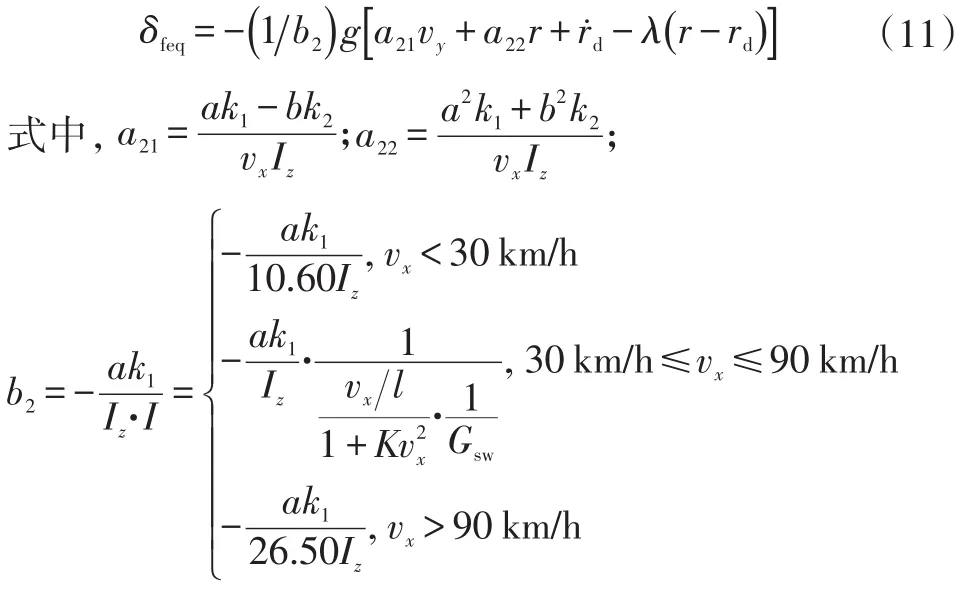
分别为线性二自由度模型的矩阵元素。

主动前轮转向的滑模控制律由两部分组成。一部分为等效控制律，确保系统能够到达滑模面。另一部分确保系统在有扰动的情况下，仍能收敛于滑模面，滑模控制结构为：

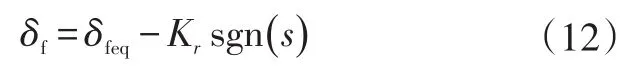
式中，δf为总输入转角；sgn为符号函数；Kr为滑模切换增益。

为了保证系统闭环稳定，Kr的选择应满足李雅普诺夫函数必要条件[21]：

符号函数sgn在零点附近不连续，导致估计值在滑模面两侧的高速切换中产生高频抖振。为消除抖振，用饱和函数代替符号函数：

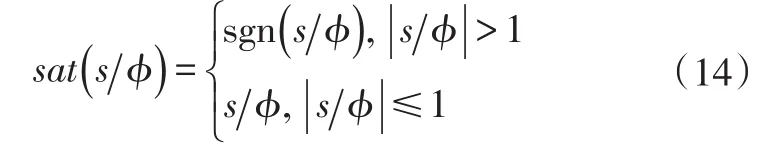
式中，φ为边界层厚度。

滑模面附近边界层如图3所示。由图3可以看出，φ越小，系统的状态误差越小，本文取φ=0.05。

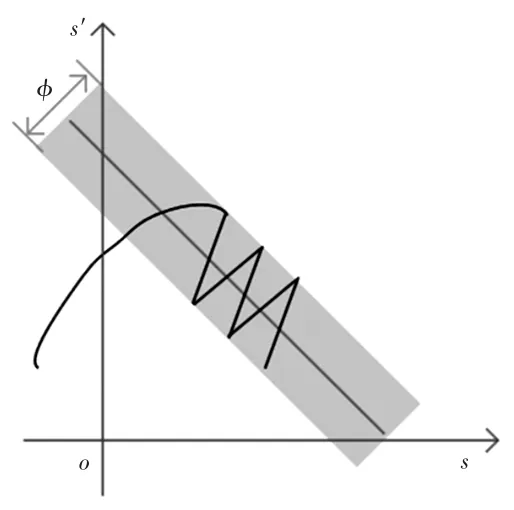
图3 滑模面附近边界层

滑模控制律为：

式中，δAFS为主动前轮转向机构提供的附加转角。

4.2 仿真分析

目前的主动前轮转向滑模控制策略是先将传动比I视为一固定值，代入二自由度车辆模型求出稳态横摆角速度，与车辆的实际横摆角速度进行比较，求出需要提供的附加转角，从而达到改变传动比的目的[22-23]。本文将这种变传动比方式称为普通变传动比，用于对本文所提出的基于理想变传动比规律的主动前轮转向滑模控制策略进行仿真对比及分析。

在MATLAB/Simulink中搭建七自由度整车、Dugoff轮胎、固定速比转向器、滑模控制器等系统模型进行仿真，主要仿真参数见表1。

滑模控制结构如图4所示，首先设计滑模控制策略进行理想横摆角速度跟踪，得到附加转角，将叠加后的输入转角输入固定速比转向器转化为对应的车轮转角，将其输入到整车模型，实现基于理想变传动比的主动前轮转向滑模控制，Simulink控制框图如图5所示，其中vx0为初始车速。

图4 主动前轮转向滑模控制结构

在转向盘转角幅值为30°，车速分别为20 km/h、80 km/h和120 km/h条件下，利用正弦输入模拟车辆行驶过程中的换道操作，角阶跃输入模拟紧急转向操作，进行仿真分析，仿真结果如图6、图7所示。

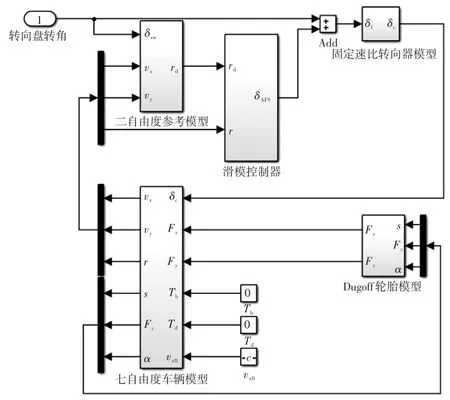
图5 Simulink仿真控制框图

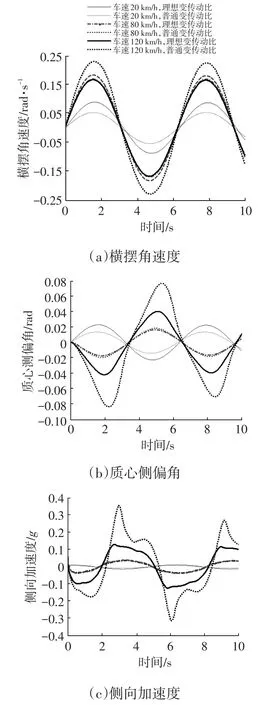
图6 不同车速下车辆的正弦输入响应

由图6、图7可以看出：车速为20 km/h时，理想变传动比车辆的横摆角速度、质心侧偏角、侧向加速度与普通变传动比车辆相比，响应幅值均明显增大，表明此时车辆转向更为轻便；当车速增加至80 km/h和120 km/h时，与普通变传动比车辆相比，理想变传动比车辆的质心侧偏角、横摆角速度、侧向加速度的响应幅值均变小，表明此时车辆具有更好的转向稳定性能，驾驶员的路感更强。

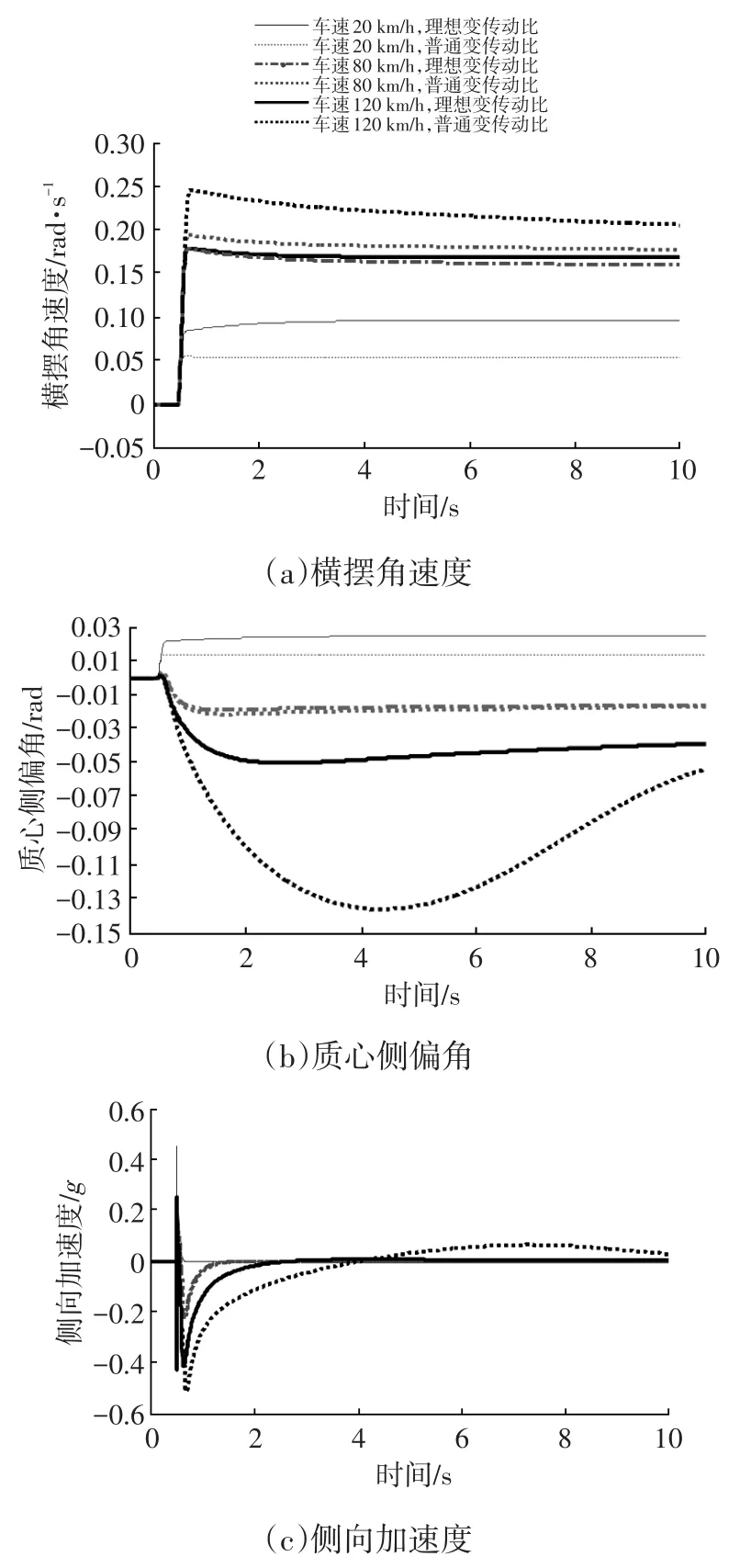
图7 不同车速下车辆的角阶跃输入响应

在较高车速（120 km/h）下进行转向操作时：普通变传动比车辆的质心侧偏角、侧向加速度响应幅值出现较大的波动，车辆转向稳定性明显变差；基于理想变传动比控制的车辆能够更快地达到稳定状态，且大幅度减小响应幅值。可见理想变传动比控制对于提高高速行驶车辆的转向稳定性具有重要意义。

5 结束语

本文利用七自由度车辆模型、Dugoff非线性轮胎模型、固定速比转向器模型建立了用于主动前轮转向分析的系统模型，确定了固定横摆角速度增益下的理想变传动比规律，并提出基于该理想变传动比的主动前轮转向附加转角的滑模控制策略。研究结果表明，与普通变传动比控制相比，基于理想变传动比规律的主动前轮转向滑模控制策略可有效保证在低速时转向车辆具有更好的转向灵敏度，转向更为轻便省力，高速时大幅度减小转向车辆的响应幅值，具有更好的操纵稳定性。基于理想变传动比规律的车辆具有更为理想的转向性能。

进一步研究方向：针对高速行驶的车辆在低附着路面上转弯时极易发生侧滑的情况，研究如何利用模型预测控制理论补偿预测力与参考值之间的差值实现跟踪控制，进一步提高车辆高速转弯工况下的稳定性。