基于遗传算法优化的支持向量机在岩性识别中的应用
2019-07-09张昭杰方石
张昭杰,方石
吉林大学 地球科学学院,长春 130061
0 引言
乌夏地区侏罗系地层沉积环境和地质条件较为复杂,该地区岩性呈现出纵横向变化大、成分成熟度低以及非均质性强等特点,使得各种岩性与其测井响应特征多数为非线性关系。且该地区地层普遍含泥、含砾,属于复杂岩性地层,对岩性识别工作产生了许多不利影响。同时,考虑到成本因素导致岩芯资料缺乏,而岩屑录井采样间隔较大,人为干扰因素过多,因此无法完整准确地恢复整套地层的真实岩性[1]。目前,常规的测井岩性识别手段包括交会图法[2]、聚类方法[3]及人工神经网络[4]、主成分分析[5,6]等数理统计方法。两参数的交会图一般只能对测井特征明显的岩性进行有效识别,很难做到全井段或解释井段的岩性识别[7];聚类分析方法在对岩性进行识别时,选择不同数量的聚类中心对识别精度影响较大;人工神经网络方法因其网络拓扑结构难以确定,易陷入局部最小值等问题,导致岩性识别效果不佳[8];主成分分析法虽然可以有效降低测井数据维度从而提高识别精度,却容易忽略数值较小但对岩性判定影响较大的测井属性[9]。
支持向量机(Support Vector Machine,SVM)是Vapnik于1995年基于结构风险最小化原则提出的一种新型机器学习分类方法[10]。本文在支持向量机方法的基础上,利用遗传算法对其核函数和惩罚因子进行寻优,在岩芯资料有限的情况下,利用测井数据对乌夏地区复杂砂砾岩岩体进行岩性识别,并对BP神经网络预测结果和利用遗传算法优化的支持向量机预测结果进行了比较,论证了使用支持向量机模型对岩性进行识别的高效性与可行性。
1 算法理论
1.1 支持向量机
支持向量机是一种二类分类模型,是在特征空间上的间隔最大的线性分类器,并且能寻找到全局最优解[11]。支持向量机的基本思想是求解一个能够正确划分数据集的分离超平面,并且保证这个超平面的几何间距最大化,对于线性可分的数据集,其最大几何间隔的超平面是唯一的。其基本结构如图1所示。

图1 支持向量机示意图Fig.1 Support Vector Machine
一般来讲,对于一个给定的训练数据集D={(x1,y1),(x2,y2),…,(xn,yn)},其中,实例xi属于输入空间,xi∈X=Rn,yi∈Y={+1,-1},i=1,2,…,N。对于线性可分数据集,通过间隔最大化得到的分离超平面可表示为:
ω·x+b=0
(1)
式(1)中,ω为法向量,决定超平面的方向;b为位移项,决定超平面和原点之间的距离,可用(ω,b)来表示。其将特征空间划分为两部分,法向量指向的一侧为正类,另一侧为负类。对于(xi,yi)∈D,若yi=+1,则有ω·x+b>0;若yi=-1,则有ω·x+b<0。令
(2)
为了让训练数据集的正例和负例距离这个超平面尽量远,使得分类间隔最大,即满足:
(3)
对于非线性分类问题,对原始样本进行划分是无法通过建立最优超平面来完成的。对于这样的问题,可以在支持向量机中加入一个松弛变量放宽约束并添加一个惩罚因子来进行解决,同时对式(3)使用拉格朗日乘子法,在式中添加拉格朗日乘子对其进行约束,将大间隔划分超平面问题转化为对偶问题:
(4)
即:
(5)
0≤αi≤C
求解上述方程后得到:
(6)
式(6)中,αi为拉格朗日乘子,xi为第i个特征向量,yi为xi的类标记,k是支持向量机数目,b是分类阈值。
非线性分类问题无法用直线(线性模型)把正负类数据分开,笔者通过引入“核函数”(kernel function)的方式,将原特征空间数据集通过非线性转换映射到高维特征空间,利用线性分类方法在高维空间中求解最优超平面[12]。最常用的核函数有径向基核(RBF),多项式核和Sigmoid核,本文拟选择采用径向基核(RBF)作为支持向量机分类模型的核函数[13]。
(7)
1.2 遗传算法
遗传算法(Genetic Algorithm,简称GA)是基于遗传学机理和模拟自然界生物进化过程而形成的一种过程搜索最优解的算法,是一种自组织、自适应的人工智能技术[14],15]。支持向量机模型的建立本质上就是寻求其两个关键参数:核函数参数σ和惩罚因子C[16]。这两个参数的确定对模型的精度和泛化能力具有很大影响[17]。用遗传算法搜寻支持向量机岩性识别最佳参数的流程为:
① 将标准化后的岩性样本测井数据输入到支持向量机模型中作为训练样本。
② 随机产生一组核函数参数和惩罚因子,使用二进制编码方案对其进行编码,随机生成初始群体。
③ 计算初始群体的误差函数,从而确定群体适应度。误差函数值越小,则表明适应度越大。
④ 执行交叉和变异算子,按最优保留,取代最差为原则对上一代群体进行处理。
⑤ 判断是否满足条件,否则返回步骤②,直到得到最优参数组合为止。
2 岩性识别实例
乌夏地区地处准噶尔盆地西北缘,又被称为乌夏断裂带(图2),其侏罗系地层总体上呈北高南低,并向盆地内变厚的楔状展布特点[18]。其中下侏罗统齐谷组地层以辫状河三角洲沉积为主,发育了泥岩、泥质粉砂岩、中细砂岩和砂砾岩等多种岩性[19,20]。本文以侏罗系地层为例,结合录井岩性和测井资料,总结层内不同岩性对应的测井响应特征,提取对岩性敏感的测井响应参数,建立GA-SVM岩性识别模型。

图2 准噶尔盆地乌夏地区位置图[20]Fig.2 Location map of study area
由于研究区岩性较为复杂,因此基于现有资料将研究区划分出泥岩、细砂岩、中砂岩及砂砾岩四种主要岩性。本文在乌夏地区有准确岩芯定名资料的20余口井中,选择了620个具有代表性的岩芯数据,其中泥岩150个,泥质粉砂岩115个,中细砂岩165个,砂砾岩190个,提取这4种岩性所代表的测井曲线中的声波时差(AC)、中子孔隙度(CNL)、密度(DEN)、自然伽马(GR)地层电阻率(RXO)数据建立了5维4类的样本空间,表1总结出了乌夏地区4种岩性的测井响应特征。从表1中可以看出,每种岩性对应的测井响应特征差异比较明显,这就意味着可以利用支持向量机在非线性数据集上的分类优势对岩性进行分类。同时本文对所有样本的测井数据进行归一化处理,统一纳入到(0,1)的范围内,以消除因特征量纲不同所带来的影响。
3 岩性识别结果对比
支持向量机分类模型准确度的高低很大程度上取决于对该模型核函数参数σ和惩罚因子C的选择,参数选取不合理会直接影响预测精度。因此本文选择径向基核函数作为支持向量机的核函数,通过遗传算法计算出其最佳参数值为(19.346,6.1539)。
在获得最佳的核函数参数σ和惩罚因子C后,将500个岩性样本作为学习集(表2)进行训练,得到相应的支持向量机模型,120个岩性样本作为验证集用以检验该模型在研究区的岩性识别能力,并与BP神经网络的预测结果进行比对。表3列出了部分测试样品输入的测井参数及识别结果,表4列出了所有测试样品的分类情况。

表1 乌夏地区岩性平均测井响应范围及响应特征

表2 部分训练样品的测井参数值及岩性标识
注:1.泥岩;2.细砂岩;3.中砂岩;4.砂砾岩.
从表3、表4列出的结果可以看出GA-SVM模型在岩性识别方面具备较大的优势,对比用相同的样本进行训练得到的BP神经网络模型,GA-SVM模型的识别准确率明显更高。其中,GA-SVM模型对泥岩和中砂岩的识别准确度最高,分别达到88.6%和88.3%,其次是砂砾岩,准确度为78.6%,最差的是细砂岩,为74.1%。通过对比和分析发现,识别错误的样本主要是将细砂岩误判为中砂岩和泥岩,由于这两种岩性物性相似,导致其测井响应特征差异不大。另外,井壁坍塌、裂缝以及岩芯编录过程中的人工识别误差也是产生误判的原因。总体而言,在120个验证样品中,GA-SVM方法识别正确的样品数为98个,准确率为81.6%, BP神经网络的识别准确率仅为65%。
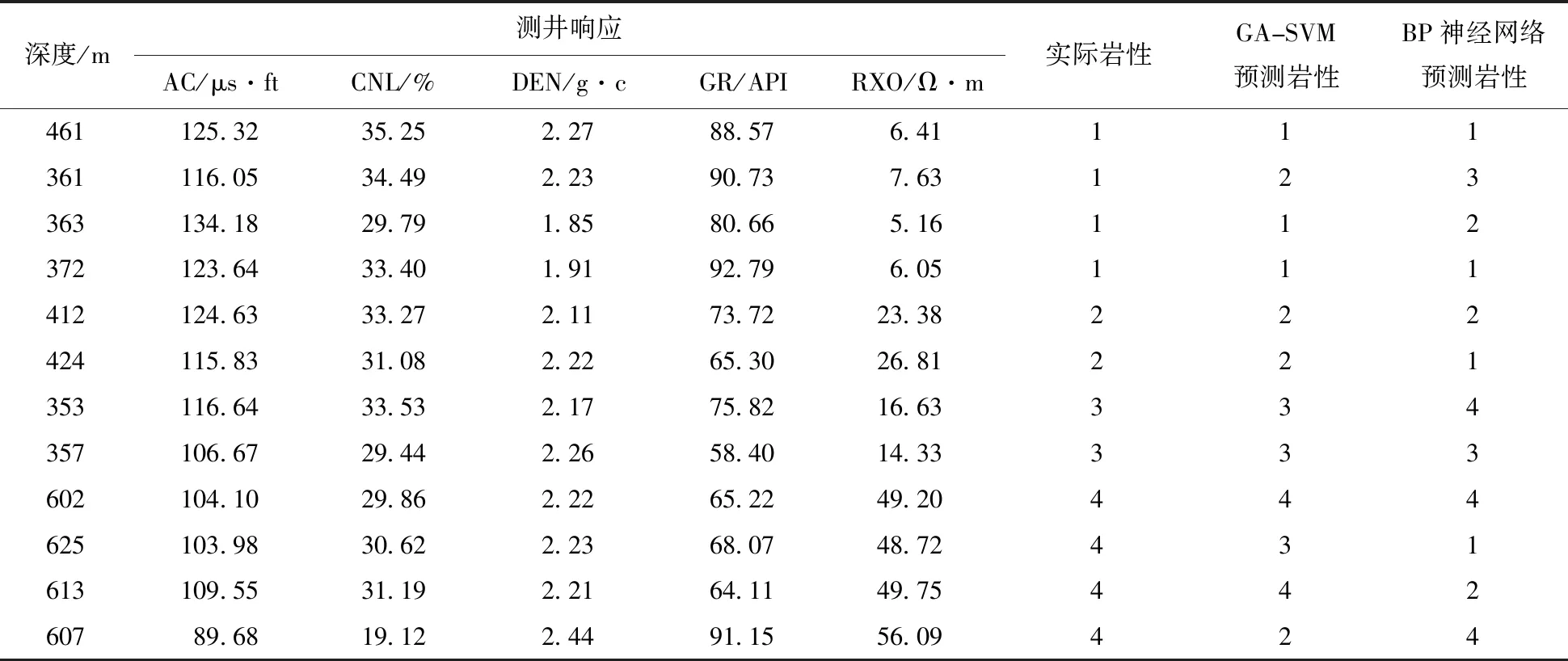
表3 部分测试样品的测井参数值及识别结果

表4 岩性识别统计结果
4 结论
(1)通过建立测井数据和岩性的对应关系,利用支持向量机在非线性问题和小样本情况下的分类优势,对砂砾岩岩性进行划分。
(2)砂砾岩形成环境复杂,非均质性强是造成砂砾岩岩性判别的难点。
(3)遗传算法的全局搜索策略能够寻找到最优的支持向量机参数,利用遗传算法对支持向量机岩性识别模型进行优化调整,实际数据预测得到的总体准确率为81.6%,优于BP神经网络。
