油页岩原位加热温度场测温误差的评价

2019-07-09刘泽宇刘小杨牛明璇马建雄薛林福

世界地质 2019年2期

刘泽宇，刘小杨，牛明璇，马建雄，薛林福

1.吉林大学地球科学学院，长春 130061；2. 中国国土资源航空物探遥感中心，北京 100083

0 引言

原位开采技术是一种高产出比、可持续发展的环境友好型开采方式，也是中国页岩气工业能否大规模产业化的关键所在[1-3]。由于中国油页岩资源普遍品位低，埋藏深[4]，国外的一些成熟技术(ICP、ElectrofracTM、EGL等)不能直接应用[5]，因而研发适应中国油页岩的原位开采工艺是当前亟待解决的问题之一。有别于常规开采方式，原位开采需要借助一定的载体(高温蒸汽、电热器、射频等)向油页岩层输入热量，使之在地下热解生烃，继而回收页岩油气。因此，了解油页岩层温度场的分布情况对于设计开采方案、确定热解进度、调节开采计划至关重要。

前人对该问题多有研究：Fan et al.[6]针对ICP技术利用非破碎高渗透性油藏模型对采暖井的井型、温度和井距进行了分析；施卫平等[7]、薛晋霞等[8]探讨了电加热法油页岩的升温过程；高孝巧等[9]探讨了原位加热过程中的热应力变化规律。但这些研究更多是从整体上预测讨论油页岩层的热史分析，很少关注地下温度监测这一过程。由于原位开采过程具有不透明性，油页岩温度场只能通过设置于地下特定位置的温度传感器来获取。而受当前钻井技术水平和施工工艺的限制，测温传感器无法直接接触地下油页岩层，不能保证测温的准确性。本文针对注气加热原位开采技术开展数值模拟试验，系统分析评价了测温误差的影响程度，对优化开采工艺有良好的借鉴作用。

1 常规测温过程的局限性

原位开采技术目前在中国仍处于探索阶段[10]，已提出的技术大多停留于理论，其中，原位压裂化学干馏技术(简称IFCD)[11]是当前为数不多的进行了实验研究的地下干馏技术。该技术配套的测温系统是常规的“监测井测温法”，即在钻采区设置温度监测井，以水泥等材料将热电偶传感器封装于铁质套管中，再将套管埋入地下以测量不同深度的温度值。在注气速率接近恒定的时段内，监测井记录下的温度数值如图1所示。但由于温度传感器与地下油页岩层并没有直接接触，其测量值实际上是该深度下固井水泥的温度，而非岩层真实的温度。

常规测温过程的局限性主要体现在两个方面：

1)测温点密度有限，图1仅有两个测温点(热源间距0.5 m、2 m)位于油页岩层中，其他测温点均处于盖层之中，导致横向对比的样本数量不足，难以归纳变化规律。

2)封装材料、监测井的铁质套管和油页岩间存在截然的物性差异，势必会导致测量误差，如若不厘清误差影响规律就加以忽略，极可能造成结论性错误。

2 测温过程的数值模拟

本文参考IFCD技术设计了数值模拟实验方案，用以验证测温误差的存在并加以量化。考虑到实际开采过程尚存在一些不确定的影响因素，在IFCD技术的基础上适当简化和调整，减少了井和压裂隙的数量，以排除布井方式、压裂隙分布密度等变量对温度场的影响。假定原位注蒸汽过程中流体黏性力做功为0，紊流粘性各向同性，且不考虑油页岩内部的水分蒸发与化学反应，本文基于三维有限体积方法对该过程进行了数值模拟。

出于计算效率和稳定性方面的考量[12]，本文采用时均N-S方程组(能量方程、动量方程和质量方程)求解流固耦合问题，并同时启用湍流模型(K-epsilon两方程模型)来确定高温流体的三维非定常流动。

2.1 计算模型与边界条件

为保证模拟结果的可参照性，本文使用的计算模型基本还原了扶余试验田的IFCD原位开采方案，采用相同的开采参数与布井方式(图2)：

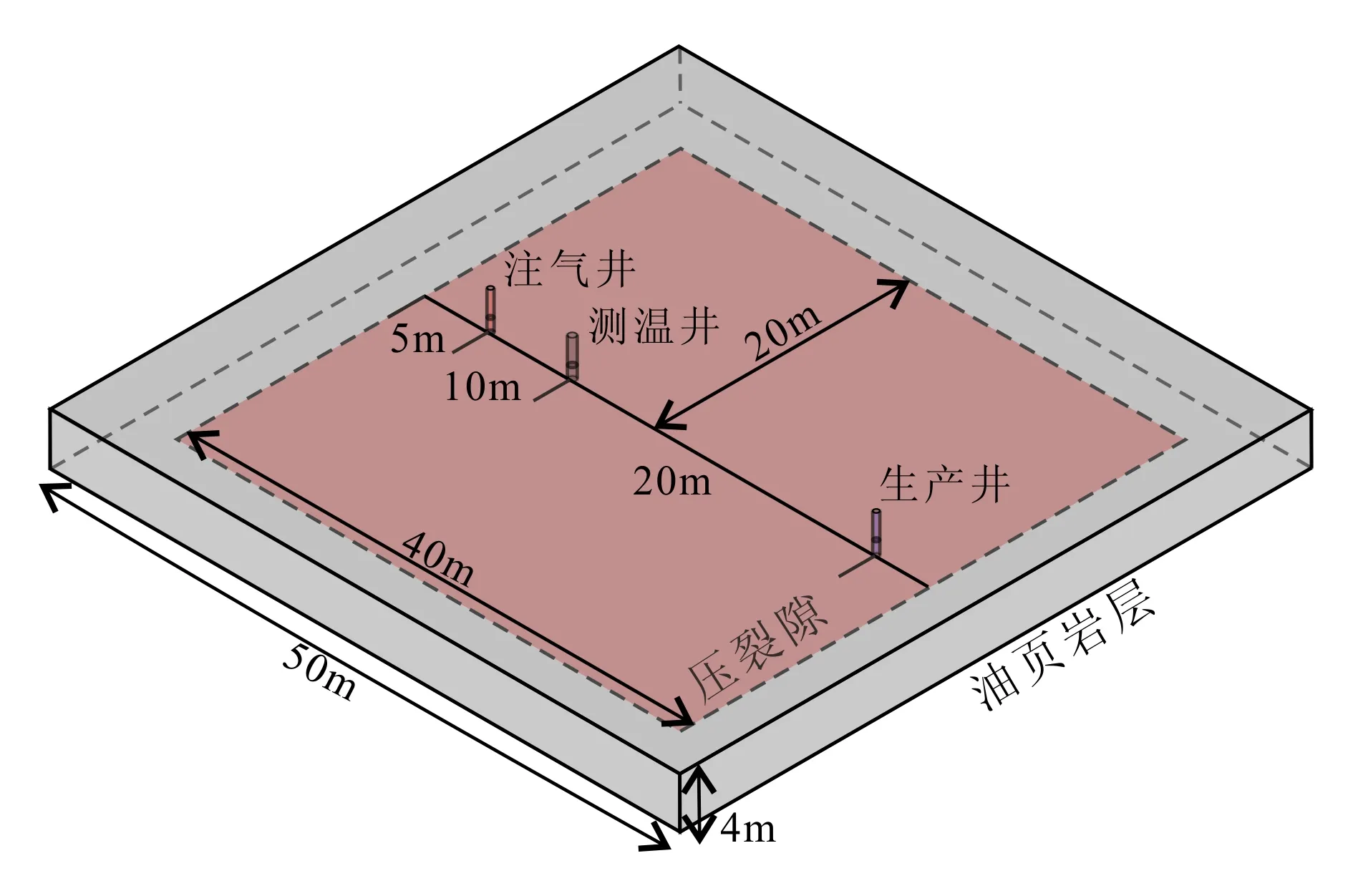
图2 计算模型示意图Fig.2 Diagram of calculation model

本文截取开采试验区的重要区域进行模拟，设置油页岩层为50 m×50 m×4 m的长方体，产状水平。将压裂隙抽象为一个40×40的长方体，厚2 mm，置于油页岩层中央(距岩层上表面2 m)，使得整个流体部分相互连通且形成对流加热体系。注气井与生产井之间的距离为30 m，并于距离注气井10 m处设置监测井，3口钻井均直接贯穿油页岩层，内径15 cm。监测井由外侧铁质套管和内部充填的水泥组成，套管厚10 mm。油页岩层原始温度设置为300 K，向注气井内以5 m/s的速率注入900 K的高温蒸汽，设置油页岩层外壁温度为300 K。

本文使用的物性参数来自扶余试验田钻孔取得的油页岩岩芯，属上白垩统青山口组(K2qn)，埋深150 m。基于Gustafsson的瞬变平面热源法[13]，利用Hot Disk 热常数分析仪能够精确测量油页岩的热导率和比热容，并通过对离散样品求取均值进行确定。实验获得的油页岩物性参数如表1所示。

2.2 测温误差的验证

热史模拟结果显示：加热约800 d时监测井平均温度达到稳态(823 K)，约900 d时油页岩平均温度不再变化(527 K)。油页岩的升温过程明显滞后于监测井，加热360 d时，监测井的温度就达到了775.6 K，此时已经完成了整个升温过程的90%。而油页岩层的升温进程耗时更长，直到630 d时(此时平均温度为503.6 K)才接近总进程的90%。由于二者升温速率的不同，油页岩层和监测井之间的温度差也随加热时间而变化，在420 d时达到峰值，平均温差最大值为326.6 K，最终平均温差约296.2 K。

显然，热物理性质和体积的差异决定了油页岩层和监测井不可能同步升温，相较于油页岩这一热的不良导体而言，金属材质的监测井显然能够更快地完成纵向上的热传导，从而导致监测井附近出现温度异常。

本文同时模拟了“无监测井”的情况作为对照，两种模拟情况的数学模型、边界条件及参数设置完全相同。以加热稳态时刻为例(图3)，地下温度场理论上应当以充满热流体的压裂隙为中心纵向上向两侧递减，但监测井的存在却对局部温度场产生了影响。监测井附近区域的油页岩温度小幅升高，而监测井内部纵向上温度分布却趋于均一化，部分消除了由热源间距增大所引起的温度衰减现象。内置于监测井中的温度传感器必然也无法规避和排除监测井的影响，从而产生测量误差。

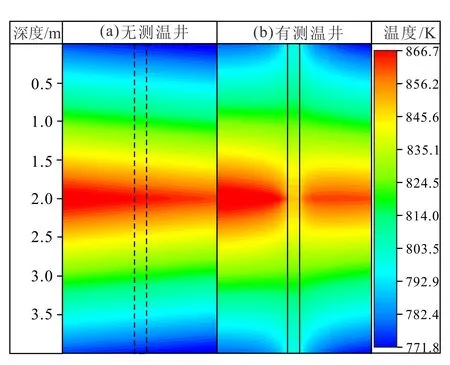
图3 加热稳态时监测井位置的局部温度云图Fig.3 Contours of local temperature near monitoring well in steady state

测温误差有三个主要来源：1)热传递过程中的热损耗；2)与环境热交换过程中的热耗散；3)不同材料之间的导热性能差异。其中，前二者不取决于监测井，而第三个误差来源才是决定测温误差大小的根本性因素，可称之为“差异性热传导效应”。由于热物性差异，监测井的实际热传导效率、升温速率均明显高于油页岩层，甚至还会改变局部温度分布状态。在没有其他措施辅助测量的情况下，仅通过常规测温井很难达到实时监测地下温度场的目的。

3 测温误差的评价

3.1 测温误差评价方法和指标

由于三维非稳态温度场分布是空间与时间的函数[14]，相应地，测量误差也与加热时间和位置有关。

为定量评价测温误差的大小，通过对比两种模拟情况，能够直观地衡量监测井对温度场的扰动作用，从而对测温误差加以量化和评估。

分别提取监测井中心位置的温度值组成两组时间序列数据，取无监测井时的温度值减去有监测井时的温度值作为测温误差。常用且有效的误差评价指标包括绝对误差、平均误差、平均绝对误差、平均相对误差及均方根误差等，各指标的计算公式如表2所示。其中，绝对误差与平均误差的绝对值大小反映测量值相对于真值的偏离程度，正负符号仅表示偏离方向，不能用于比较。本文探讨的“测温误差”主要由以上6个指标体现。

表2 误差评价指标及计算公式

注：式中x为真值(无监测井时温度值),x′为测量值(有监测井时温度值)，n表示统计样本数量.

3.2 加热时间对测温误差的影响

模拟结果表明(图4a)，随着加热时间的增加，测温误差将呈现出先升高后降低的趋势。监测井和岩层的升温及传热过程存在时差，致使加热前期测温误差持续扩大，约65 d时将达到峰值，此时eME、eMAE和eRMSE将分别达到34.9 K、-20.8 K和32.14 K。加热65 d后，监测井温度场已经接近稳态，而岩层加热程度却仍在增加，差异性热传导逐渐被消除，误差降低就是这一过程的具体体现。加热600 d时各误差评价指标均开始收敛，此后的变化已经微乎其微，加热稳态时的eME、eMAE、eRMSE分别将降低到9 K、-5.2 K和10 K。

eMRE曲线显示(图4b)，在加热前期，测温误差最大能够达到实际温度值的8.5%，平均为3.15%，除前10 d的“预热期”外，eMRE在加热前120 d内都保持在5%之上。在整个模拟过程中，所能观测到的et的极值为76.5 K和-52.7 K，这意味着在某特定时间和位置，测量值和真值之间出现超过50 K、乃至70 K以上的偏差，其相对误差已逾15%。

3.3 热源间距对测温误差的影响

除受加热时间的影响外，空间位置也是测温误差的决定性因素，二者共同控制了每一个位置的测温误差大小。从时间-误差分析可知，加热65 d是一个关键时间点，此前平均测温误差不断增加，至此达到峰值，而后持续降低直至收敛于稳态。

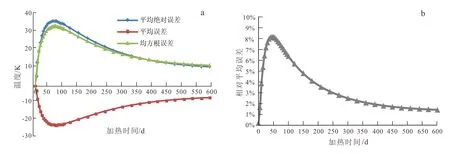
图4 测温误差随加热时间的变化曲线Fig.4 Variation curve of measurement errors with time

不同深度下的绝对误差的变化如图5所示，2.0 m深度是热源(压裂隙)的所在位置，测温误差在其两侧对称分布，并由临近区域内的正值逐渐变为负值。加热65 d时绝对误差介于-50.19 K到69.86 K之间，测温误差最大值出现在最靠近热源处；而至加热稳态时，绝对误差介于-24.83 K到12.98 K之间,测温误差最大位置则变为了热源的远端。从加热全过程测温误差的变化可知：随着热源间距的增加，测温误差先减后增，且测量值由“低于真值”逐渐变为“高于真值”，绝对误差与热源距离之间符合指数变化函数分布。

图5 测温误差随深度变化曲线Fig.5 Variation curve of measurement errors with depth

与温度场的分布类似，测温误差也具有空间对称性，控制时间因素时，相同热源间距下测温误差基本一致。相较于加热时间，热源间距对于测温误差的影响程度更显著，当热源间距为0.5 m时测量误差最小，但当热源间距过小或过大都会使得测量值严重偏离真值。若将测温点设置在热源间距0.05 m处，测量值最多可以比真值低75.86 K，全过程平均低46.87 K；若将测温点设置于热源间距2 m处，测量值最多可比真值高52.71 K，全过程平均高34.88 K(图6)。

图6 不同热源间距下测温误差变化曲线Fig.6 Variation curve of measurement errors in different heat source separation distance

在本文模拟的情况中，直接与热源接触的部位每提升1 K平均需要约19 h，整个油页岩层日均升温仅0.33 K±，85.4%的区域月均升温不到10 K。然而全程测温平均偏差达到了19.35 K，监测井仅有15.5%的区域(热源间距介于0.31～0.62 m之间)测量值与真值相差<10 K，由此可见其测温可信度有待商榷，测温误差的严重性应予重视。

基于上述分析，在当前的技术下的一个可行方案是：增设一个井深较浅(不贯穿压裂隙)的温度监测井，使之与油页岩层处于类似的升温环境中，该井所获得的测温数据能够同原有数据进行差分，以期消除差异性热传导的影响。考虑到误差成因，测温系统的最佳改进方向应当是通过特定技术(如射孔)令温度传感器直接接触页岩层，从而彻底消除系统误差。