地表水环境数学模型研究进展

李一平，施媛媛，姜 龙，朱向宇，龚 然

(1.河海大学环境学院，江苏 南京 210098； 2.清水源(上海)环保科技有限公司，上海 201107；3.南京工程学院环境工程学院，江苏 南京 211167)

水环境保护是国家水安全保障的重中之重，掌握新形势下水环境演变过程是开展水环境保护工作的关键[1]。研究水环境问题的手段主要包括野外观测、室内试验和数值模拟，其中水环境数学模型扮演着越来越重要的角色。地表水环境数学模型(surface water environment numerical models，SWENM)主要分为水动力学模型、水质模型和水生态模型，基本原理是将气象条件、水动力条件、边界条件等因素进行定量化约束，通过求解方程组，获得污染物的时空分布特征及迁移转化规律，分析和判别各环境因子间的相互关系，实现模拟与预测等功能。

目前，已研发的地表水环境数学模型有数百种，算法及应用的差异给水环境决策带来了一定的困难。现有综述论文对3类模型的介绍不够全面，水文领域更关注水动力模型，环境领域又更注重水质模型，水生态模型因其复杂性及涵盖面广难以进行整合归纳。此外，关于模型模拟精度影响因素的综合探讨比较欠缺。因此，归纳比较各种模型的适用范围、强化模型敏感性和不确定分析、辨析模型精度的影响因素等均有利于地表水环境数学模型的精准优化发展。鉴于传统模型应用的时空局限性，“3S”、云计算、人工智能等新技术的引入以及模型综合化和法规化，将成为水环境模拟与预测领域未来的研究热点。

1 地表水环境数学模型的研究现状

1.1 水动力学模型

近代水动力学起步于Navier-Stokes方程(简称N-S方程)，随后，Saint-Venant于1871年首次提出了计算一维河道及河网水流的一维水流运动基本方程——Saint-Venant方程。由此，水动力学模型逐步应用于河流、河网；20世纪60—70年代，随着Saint-Venant方程的广泛应用，各种求解方法的数值稳定性和精度问题得到深入研究。平原地区河道交错，流向流速易受潮汐、水利调度等影响而催生了涉及面更广的河网模型[2]。在湖库方面，Hesen于1956年最早提出浅水平面二维水动力学模型。之后的模型侧重于水流运动，包括风生环流[3-4]和吞吐流，以及在深水湖库还因温度分层而存在垂向密度流[5-6]。

随着计算机技术引入水动力学，计算水动力学在计算方法、网络技术、紊流模型、大涡模拟等方面的新理论和新方法也为水动力学模型领域提供了有效借鉴[7]。直接数值模拟(direct numerical simulation,DNS)、Reynolds平均模型(Reynolds average Navier-Stokes,RANS)和大涡模拟(large eddy simulation，LES)等方法得以应用，进一步修正了N-S方程，典型的紊流模型有k-ε模型和v2f模型等[8-9]。此外，水动力学模型在洋流领域的应用研究推动了紊流机理的深入探索，洋流模型由最初的普林斯顿海洋模型(Princeton ocean model，POM)发展至浅海三维水动力模型(3D estuarine coastaland ocean model，ECOM)，直至如今更为完善的有限体积海岸海洋模型(finite volume coastal ocean model，FVCOM)。在河口海岸区域，水动力学模型解决了潮汐作用下的紊流混合[10]、因盐度差而形成的密度流以及因径流和盐度密度流产生的入海口滞留问题[11]。

当前，水动力学模型与其他模型(流域水文模型、波浪模型和泥沙模型等)的耦合应用实现了空间多维度的模拟。例如，外夹河流域的耦合模型以水文模型计算的流量作为水动力学模型的边界条件，成功实现了丘陵、平原混合地区的洪水预报[12]；太湖透明度模型[13]基于浅水波浪数值模型(simulating waves nearshore，SWAN)，耦合了波浪模块和湖流三维模型，动态模拟了太湖波浪和湖流的生消过程；三维水动力模型也常常应用于探究泥沙输移规律[14]及鱼道模拟[15]。

1.2 水质模型

自1925年Streeter和Phelps建立了BOD-DO耦合模型(S-P模型)以来，水质模型已经发展了90多年。水质模型基于水动力学模型，根据物质守恒原理概化污染物在水中发生的物理、化学、生物化学变化过程。主要分为4个发展阶段[16]：

第一阶段(1925—1965年)：简单的氧平衡模型阶段。集中研究氧平衡，部分涉及非耗氧物质，不断修正S-P模型。

第二阶段(1966—1985年)：水质模型迅速发展阶段。考虑污染物不同形态的影响机制，20世纪70年代初，美国的研发机构开始推出QUAL-Ⅰ、WASP(water quality analysis simulation program modeling system)等综合水质模型软件，后续列入其他污染源、底泥、边界的作用，研发的QUAL系列模型应用于河流综合水质规划管理[17]。

第三阶段(1986—1998年)：水质模型深入研究、广泛应用阶段。更多复杂的水质过程被纳入模型系统，例如，考虑沉积物“土-水”界面动态过程的沉积成岩模型[18]；模拟对象涵盖河流、湖泊(水库)、河口、海岸带等。

第四阶段(1999年至今)：水质模型集成化、设计人性化阶段。MIKE、EFDC(environmental fluid dynamics code)、DELFT-3D等模型集成水动力学、水质、泥沙、生态等模块，并提供网格生成和前后处理工具。新兴技术也逐步被引入水质模型，人工智能提高了水质模型的预测水平[19]，遗传算法、模拟退火算法强化了参数识别[20]，神经网络明晰了河网物理结构[21]。

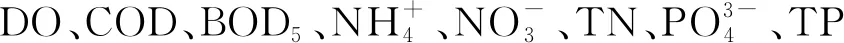
1.3 水生态模型

水生态模型是描述水生生态系统中生物个体或种群间的内在变化机制，及构建水文、水质、气象等因素连接的复杂模型，主要用于研究水体富营养化、生物富集及水域系统食物网[25]。

20世纪70年代初期诞生的简单总磷模型成为水生态模型的基石；20世纪80年代，美国和日本开发了第一批三维生态数学模型[25]。现代水生态模型考虑了自然界中多因素相互作用及时空变化。例如，Delft3D BLOOM/GEM模型能成功模拟4种不同海域的水生系统[26]；三维ERSEM(european regional seas ecosystem model)能够用于研究红海的水动力和生化动力[27]。

近年来，水生植物、鱼类迁移及生物栖息地等模块得到不断开发。江志超等[28]建立了硅藻中肋骨条藻与氮、磷关系的非线性动力学模型，发现光衰变率和营养盐是影响中肋骨条藻赤潮生消过程的关键因子。RIVER2D模型已被用于识别在研究范围内最小水深和宽度处成年大鳞大马哈鱼[29]。基于HABITAT模型建立的生物栖息地评价模型，能够反映泸沽湖水质变化对宁蒗裂腹鱼的影响[30]。此外“水生态足迹”概念的提出衍生出了水生态足迹计算模型、水生态承载力计算模型和水生态赤字或盈余计算模型[31]。

当前国内水环境模型研究主要关注水动力-水质-水生态耦合模型的应用。例如，太湖富营养化机理模型耦合了太湖三维风生湖流模型、垂向平均的二维水质模型和富营养化模型，考虑了水温、总氮、总磷和太阳辐射等因子对藻类生长的影响，模拟了藻类生消过程以及其随风生流迁移的规律[32-33]；王生愿等[34]以湖泊水动力水质响应机制为研究背景，构建了水-生态-底泥耦合的湖泊水动力水生态模型。

2 常用地表水环境数学模型

近30年来，先后涌现出许多高品质的地表水环境数学模型，例如WASP模型素有“万能水质模型”之称；还有近年应用广泛的EFDC(environmental fluid dynamics code)模型[35]，集成了水动力、水质、风浪、泥沙、重金属及有毒物质、沉积成岩和水生植物等模块。近些年国内也开发出了诸如CJK3D、IWIND等商用软件。表1列出了国内外常用的18个地表水环境数学模型。

3 地表水环境数学模型的不确定性和敏感性

模型不确定性和敏感性分析是数值建模研究的热点。不确定性分析是将模型输出中的不确定性进行量化评定[36]，而敏感性分析是研究模型输入因素和输出变化的响应关系。

水质模型不确定性的研究始于20世纪70年代，O’Neill等[37]指出单纯寻找模型最优化参数没有意义，需要确定参数的分布；之后，水质模型的不确定性得到了系统性归纳[38]，采用不同的判定标准能够确定水质模型不确定性来源及分类[39]；生态模型和统计模型开启了水环境数学模型不确定性分析的时代[40]；各种不确定性分析方法基本原理的提出，为模型参数排序及决策评估提供了有效依据[36]。

模拟结果的不确定性主要来自参数、输入数据和模型结构不确定性3个方面，其中参数不确定性指参数估计存在误差，输入数据不确定性指模型边界条件和初始条件的不确定性，而模型结构不确定性是由于人类对复杂环境系统认识的局限性，在系统建模过程中常常对一些现象和变化过程进行抽象和概化。

常用的不确定性分析的数学表达方法主要有区间数学法、模糊理论法以及概率分析法。区间数学法用于计算测量和参数估值误差引起的不确定性；模糊理论法解决具有模糊性的系统不确定问题，但难以实现定量评估；概率分析法常用于描述物理系统的不确定性，根据模型输入的概率分布来确定模型输出的概率分布，最终以概率分布的形式来表达不确定性，如蒙特卡罗(Monte Carlo)法[41]、拉丁超立方抽样法(Latin hypercube sampling，LHS)[42]、普适似然不确定估计方法(generalized likelihood uncertainty estimation，GLUE)[43]以及单纯多边形进化算法(shuffled complex evolution algorithm，SCE-UA)[44]等。

表1 常用地表水环境数学模型

敏感性分析方法主要分为局部分析方法和全局分析方法。常采用的局部分析方法是检验单个参数的变化对模型结果的影响程度(one factor at a time，OAT)。局部分析方法简单、易于实施，但响应结果较片面，无法解决“异参同效”问题。全局分析方法克服了局部分析方法的缺点，能够反映整体参数组合对结果输出不确定性的影响。全局敏感性分析方法有很多[45]：①基于回归或相关分析技术的方法，如多元回归法、响应曲面方法(response surface methodology，RSM)；②全局筛选法，如LH-OAT方法、Morris方法；③基于方差理论的方法，如傅里叶振幅敏感性检验法(Fourier amplitude sensitivity test，FAST)、Sobol方法和扩展傅里叶振幅敏感性检验法(extend FAST)；④因子设计实验[46]；⑤摩尔斯分析法[47]；⑥取样分析法[48]等。

敏感性分析常用的蒙特卡罗法属于取样分析法，能简单有效地评价多个参数对模型输出结果不确定性的贡献。LHS克服了蒙特卡罗法计算成本高的缺点，抽取的样本能更精确地反映输入概率函数的分布，不仅高度控制抽样值，又为它们留有变化的余地。基于LHS的思想，运行模拟的次数由输入变量数决定，最少可为随机变量数的1.5倍，一般为几百次[49]。

当前国内外已有对模型敏感性和不确定性研究的成功案例。李一平等[50-51]利用EFDC模型和LHS抽样方法分析了水动力模块中的5个重要参数以及4个重要的外部输入条件对太湖水位和流场分布的敏感性和不确定性，并借助原位观测简化了模型参数的率定验证；Gong等[52]基于SWAT(soil and water assessment tool)模型采用GLUE不确定性分析方法分析模型参数对模型不确定性的影响，其中针对不同的研究目标需要选取不同的似然函数[53]；Reder等[54]采用LHS和全局敏感性分析法(global sensitivity analysis，GSA)在42个参数中筛选出4个最敏感的参数以提高模型性能。

除了传统分析方法以外，基于熵的不确定性敏感性分析方法也被提出[55]，并用以识别不确定变量对随机变量和模糊变量组合系统的影响[56]。全局灵敏度测算方法(sobol)是一种两阶段不确定性量化方法，简化了不确定度量化计算过程[57]。风场、边界及底部地形的空间变化导致研究区域内的参数分布也有所差异，因此结合GIS-Lab衍生的参数空间不确定分析将成为新的研究方向。

参数不确定性和敏感性分析已成为模型构建的必要工作，通过分析可表征输出结果的不确定性对输入参数不确定性的依赖程度。对于特定的模拟目标，筛选出敏感参数、参数合理分布范围以及各个参数对模型结果不确定性的贡献率，可大幅度减少模型后续率定验证工作，同时可指导关键参数的监测工作。

4 地表水环境数学模型模拟精度关键影响因素

除由参数不确定性引起的模拟误差外，影响模型模拟精度的因素还包括模型类型及选择、网格种类、垂向坐标系统、方程离散方法、初始条件及边界条件等。

4.1 模型类型及选择

选择合适的模型是建模前应明确的重要环节，需要参考模拟对象的特性、精度要求和计算效率等。当模拟对象具有干湿交替或洪泛区特性时，应选用较为精细的水动力模型[58]；若模拟深水湖库水质，需要选用垂向二维或三维模型，考察垂向温度和水质变化[59]；若模拟重金属或有毒物质迁移转换过程，关键是构建并校验泥沙模块，其余影响因素和模块可进行一定程度的概化处理[60]。由于复杂的物理、化学、生物过程无法在模型中详述，所以模型选择不恰当可能会浪费计算时间，且不一定能达到预期目标。因此，模型的选择并非越复杂越好，在明确模拟目标后，选择合适的模型即可，这个环节需要一定的实践经验。

4.2 网格种类及垂向坐标系统

网格种类及坐标系统选择也直接影响模拟精度。常见的平面网格有矩形网格、正交曲线网格、三角形网格及四叉树网格。矩形网格基于直角坐标系便于组织数据结构，计算效率高，但不适合处理复杂的边界且不易调控网格密度。正交曲线网格是一种基于曲线坐标系统的有结构网格，可以适应不规则边界，但处理过于复杂的边界时效果不佳。三角形网格利于研究复杂地形和边界问题，易于控制网格密度，但计算效率较低。具有树状结构的四叉树网格能高度拟合复杂的自然水体，易实现水动力及物质输运数值模拟[61]。在边界和地形较复杂的位置宜采用三角形网格，在计算域内部和地形变化不大的地方宜采用矩形网格或者正交曲线网格。

垂向坐标系统一般分为平面(z)坐标、等密度(ρ)坐标和地形拟合(σ)坐标，分别对应不同的网格。z坐标模式方程简单，易于数值离散，适用于具有准水平运动特点的水体，但不易处理底部边界，在浅水区域难以满足必要的垂直分辨率。ρ坐标模式常用于密度流模拟，但在混合层、非层化水体内和底部边界层的分辨率较低。σ坐标模式实现了垂直相对分层，能够有效拟合底部地形，但斜压梯度力会有较大截断误差。对于地形复杂的水域可采用混合坐标模式，例如σ-z坐标系统适用于局部陡峭深水区，能够降低水平压力梯度误差的影响。在实际应用中，应根据岸线形状、水下地形数据和模拟精度的要求选择合适的网格及垂向坐标系统。

精细的分辨率能降低模拟误差，但会增加不必要的模拟成本。若部分区域的模拟精度要求较高，可进行局部网格加密处理，既保证拟合计算的合理性，又提高运行效率。

4.3 方程离散方法

为确保计算的稳定性和收敛性，时间步长应该足够小，通常须将时间步长减小到几分或几秒，与水动力过程模拟所需的时间步长差不多，可重现泥沙输送等水质动力学过程。目前基于有限差分法、有限体积法和有限单元法的高效数值离散计算方法、并行计算方法、集群计算方法等同时满足了精度和效度的要求[62]。有限差分法根据时间和空间步长对定解区域进行网格划分，用差商代替导数，求解方法简单但不易处理复杂边界问题。有限体积法可以根据实际问题的物理特点对任意形状网格体进行积分，且不会影响计算精度和守恒性，但是对于质量差的网格，离散的过程会产生更大的误差。有限单元法根据实际问题的物理特点对求解区域进行单元剖分，能够满足一定的精度要求，但对于二维和三维问题需要建立许多人为的节点，且求解精度过于依赖网格划分，适合分析连续变形问题。

4.4 初始条件及边界条件

初始条件包括初始水位、流速、温度等，初始条件设置是否准确，对不同的水体影响不同。模拟湖库水质时，若只依赖边界条件驱动，运行至合理的初始状态需要一定的时间且对模拟的结果影响较大。因此，模拟湖库水质时，如没有准确的实测值作为初始条件，则通常将模型运行一段时间后的结果作为初始态，称为“预热”。对于河流、河口等水动力过程较剧烈的水体，边界条件的驱动将很快覆盖初始条件，初始条件的影响很小。

边界条件包括大气边界、出入流边界、开边界的作用力、水工建筑物、取水退水边界，其中水质模块的边界条件还需考虑各种出入水体边界的水质变量、大气干湿沉降、农田面源污染、地表径流、内源释放、地下水等。在确定污染源的过程中，大气干湿沉降对水域整体的贡献不可忽略，随降雨进入水体的污染物质往往是水质恶化的关键因素[63]。边界条件还可分为垂向和水平边界条件，比如气温和风速作为模型垂向边界条件，虽然不参与直接计算模拟，但它们影响了潮流、混合和热传输等水动力过程。合适的边界条件可以有效避免模拟误差。

5 地表水环境数学模型发展趋势

目前，地表水环境数学模型正朝着系统化、综合化、法规化方向发展，模型涉及的要素越来越复杂，与许多新兴技术的结合，使得地表水环境数学模型的发展充满了机遇与挑战。

a. 模型系统的系统化、综合化和平台化。水环境模型逐步涉及水文、水动力、生物、地理等多领域，以单独模块的形式集成一体。模拟元素和模拟情景的增加拓展了模型的研究领域，比如药品及个人护理用品(PPCPs)、微塑料等新型污染物将成为新的模拟对象，藻类竞争、热量平衡等过程也逐步引入水生态模型。适用于大型流域的三维水生态模型开发，以及利用统一平台构建促使数值模拟成为流域控制与规划决策的支撑技术，将成为未来重要的发展趋势。这些将会是今后地表水环境数学模型研究的热点。

b. 与新兴技术的结合。大数据平台的参与能够有效解决边界条件、初始条件输入缺失难题；超算、云计算以及人工智能算法的应用将会大幅度提升地表水环境数学模型的计算效率和精度，比如遗传算法、模拟退火算法能够强化参数识别；VR技术丰富了模型结果的输出展现方式，实现了人性化的设计理念。在与物联网、“互联网+”、云技术的碰撞下，“3S”技术与水环境模拟集成模块的开发促进了环境因素之间的相互作用和动态变化的确定性分析，基于遥感技术的水质反演模型促进了“天地一体化”水环境监测系统的建立，能够实现数字预警、识别黑臭水体、考察海域污染，体现实时性、大尺度、高速度、动态性等优势。在GIS-Lab技术的引入结合下，风场、地形、床层等空间因素的考虑会更加全面，不确定性分析正从全局概化向区域性精细化发展，模拟过程更加真实，结果更加可靠。

c. 法规化趋势。基于GIS技术，模型库管理系统的建立促使水环境模型走上法规化管理道路。目前，美国国家环境保护局(EPA)已将97种地表水环境数学模型列入模型信息库，澳大利亚政府也针对模型选择、参数率定、敏感性分析等给出了系统推荐，我国生态环境部也正式发布了HJ2.3—2018《环境影响评价技术导则 地表水环境》，并推荐了适用于河流、湖泊、河口和海洋的数值模型。今后的发展将基于已有的模型信息库进行拓展丰富，有望实现模型运用流程的规范化操作、指导、监督。