太湖流域平原河网分流比影响因素

2019-07-09王子悦李一平董志强翁晟琳张靖林

水资源保护 2019年4期

王子悦，李一平，董志强，庄巍，翁晟琳，张靖林

(1.河海大学环境学院，江苏南京 210098； 2.宁阳县环境保护局，山东泰安 271400; 3.生态环境部南京环境科学研究所，江苏南京 210042)

分汊河道是天然河流中一种常见的河型[1]，大致可以分为单汊、群汊、分汊再汇合3种形式。作为单汊型分汊河道的基础形式和典型代表的Y型分汊河道，是分汊河道中最为普遍的一种分汊形式。分汊河道的分流特性习惯上用分流比表示，其大小和变化会影响分汊河道各支汊的兴衰, 并改变航道、决定防洪布局[3]。平原河网地区受城市化影响，逐渐暴露出水系结构破坏、河流连通受阻、河网水系自然调蓄能力明显下降等问题，而分汊河道作为平原河网的咽喉要道[4]，其分流比对平原河网的基本格局和河流主干规模有着直接影响[5]。一般来说，水深、流量、过水面积、水面宽度、流速、分流角、流向、汊道糙率、汊道比降等因素均与分流比有关[6-7]。目前国内外对分流比的研究主要从室内试验、野外观测、公式推导3个方面展开[8-10]。在室内试验方面，顾莉等[11]通过等宽直角分汊水槽试验，发现分流比的大小取决于分汊口水动力条件和支汊的回流特性；Ramamurthy等[12]指出直角明渠分流比与干流弗劳德数以及上下游纵向水深比有关，并推导出三者之间的理论关系式。在野外观测方面，唐立模等[7]分析了多次实测的赣江东西河分流比资料，认为东西河分流比主要受到流量、水位、两汊道过水条件、汊道比降4个因素的影响；胡春宏等[13]运用多元回归分析法建立了分流比的多因素综合关系式，依据滩槽过水宽度比、过水深度比、过水面积比、糙率比、流速比和主槽宽深比6个因素对黄河下游复式河道滩槽分流比进行预测。已有研究侧重于理想条件下室内平底水槽实验，难以模拟现实复杂情形。也有研究针对黄河、赣江等地形起伏较大的流域，其分流比很大程度上受到水力冲刷引起的河道演变的影响。但对于地势低平、水流滞缓、以人工河道为主的平原河网地区，如太湖地区，以上研究结论并不适用。

近年来随着城市化进程的推进，平原河网地区城市水文特性发生巨大变化，在防洪、航运、调水引流等方面受到严峻挑战[14]。分汊河道作为平原河网的咽喉要道，其分流比直接关系到这些问题的解决。本研究以典型太湖流域平原河网分汊河道——位于张家港市谷渎港的Y型分汊口为例，采用EFDC软件建立二维水动力模型，运用单因素Logistic回归和多元回归探究分流比与糙率、分汊角度、过水宽度比、干流流量、水位差的相关关系，在此基础上运用岭回归(ridge regression)建立平原河网分流比预测方程，旨在为平原河网水资源调度[15]、生态引流等提供参考。

1 研究区概况与研究方法

1.1 研究区域概况

张家港市位于太湖流域，全境地势平坦，河港纵横，河网密布，河道比降平缓，水流方向往复不定，有大小河道6 033条，总长4 477.3 km，是典型的平原河网地区。本文研究对象谷渎港入口为Y型分汊河道，研究它对研究平原河网分汊河道分流特性具有较好的参考价值。

1.2 模型介绍

EFDC(environmental fluid dynamics code)是当前广泛使用的水环境生态模型，适用范围十分广泛，可用于河流、湖库、近岸海域、河口等地表水域，从一维到三维流场模拟、物质运输(包括温度、盐度和泥沙的运输)、污染物迁移转化等过程的模拟[16]。EFDC采用σ坐标下的水动力方程，其动量方程见文献[17]。

1.3 模拟情景设计

影响分流比的影响因素有干流流量Q、糙率n、分汊角度θ、支汊过水宽度与主汊过水宽度比B和主汊水位与支汊水位差Δz。本研究采取控制变量法，分别控制其他参数不变，探究单一参数对分流比ξ的影响。分流比的计算公式见文献[18]。重复参数初始值为：Q=15 m3/s，n=0.05，θ=70°，B=0.63，Δz=0.1 m。各参数工况设置见表1。

表1 参数工况

1.4 数据分析方法

采用单因素logistic回归和多元回归进行相关性分析，显著性水平设定为α=0.05,并运用岭回归方法来克服多重共线性。为统一量纲，将各参数进行标准化处理。数据处理及分析采用的软件为IBM SPSS Statistics 23和Excel 2016，作图软件为MATLAB和AutoCAD 2017。

2 结果与讨论

2.1 模型构建及率定

2.1.1野外观测结果

河道共设3个监测点位：滋生桥、松坟桥和慕嘏桥[19]。野外采样在2018年10月26—27日进行，监测频率为每30 min一次，监测时间共8 h。各断面流量数据来源于3个监测点的手持式ADV实测数据。使用ADCP(acoustic doppler current profilers)多普勒流速剖面仪测量河道各监测点断面形态。河道分汊角度从水系图上测得为70°。部分野外观测数据见图1。

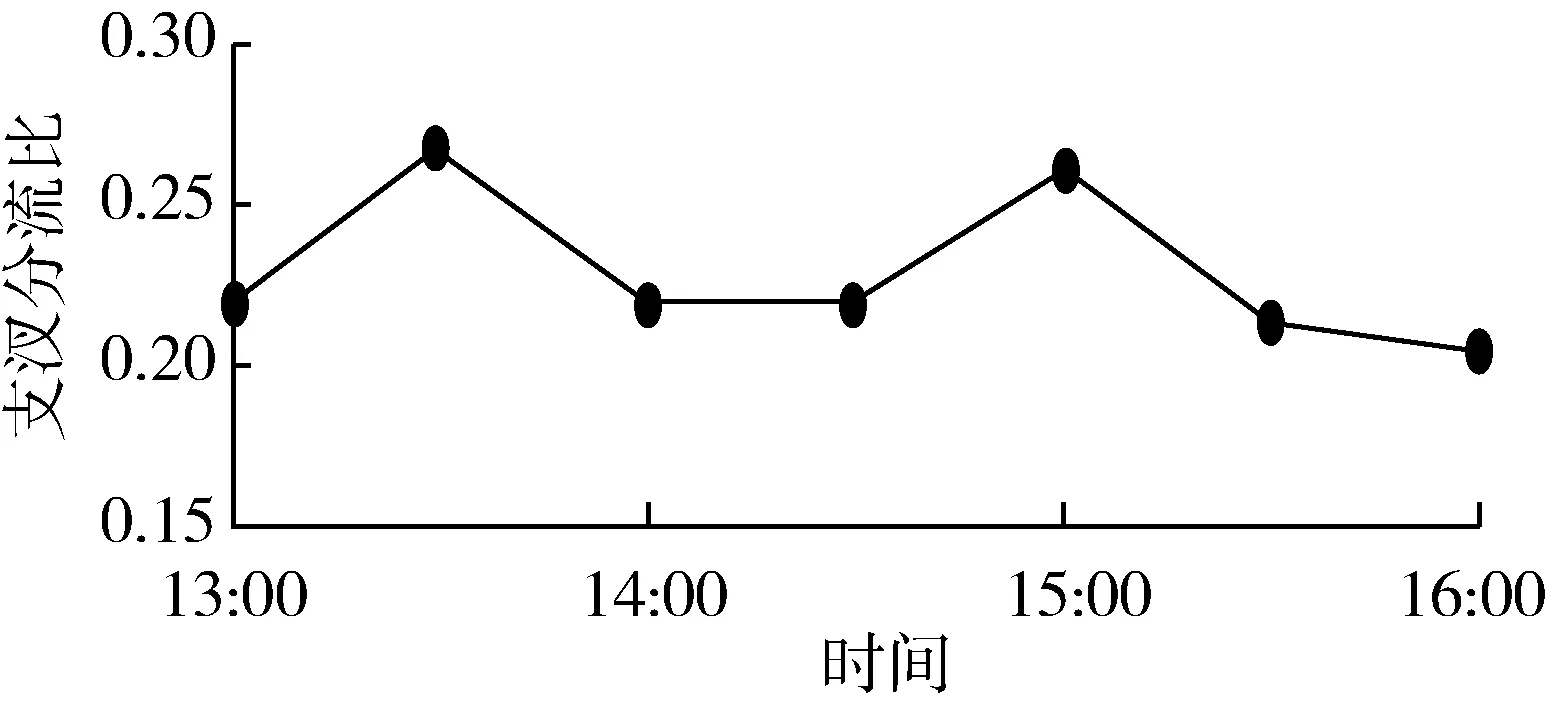
图1 部分野外观测数据

2.1.2模型构建

截取东横河长度2 442.00 m、支汊谷渎港长度917.00 m作为模型的水域边界。采用笛卡尔直角坐标划分网格，共划分22 143个网格，每个网格边长为2 m。大多数模型的断面使用梯形概化[20]，本研究根据实际监测断面点位的监测数据，建立模型底部高程文件，将实测地形资料导入后插值获得模型底高程，以求对河道断面进行最近似的模拟。将分汊河道上游入流口、支流出流口以及主汊下游出流口设置为计算边界。入流口采用流量为边界条件，两个出流口采用水位为边界条件。流量数据、水位数据由野外观测获得。模拟时间设置为10 d，时间步长0.4 s。

2.1.3模型率定

模型率定是建立水动力模型的重要步骤。利用纳什效率系数公式对流量拟合效果进行评估[21]：

(1)

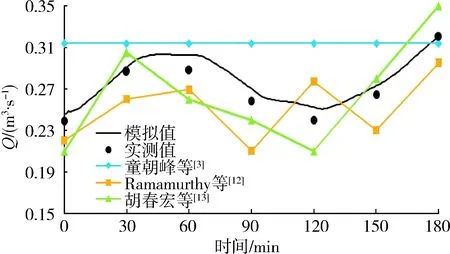
图2 分汊河道模型率定结果

2.2 河道的水体结构性连通参数对分流比的影响

2.2.1糙率的影响

图3为谷渎港入口分流比ξ与河道糙率n关系图。运用回归分析的方法建立了ξ与n的相关关系式：

ξ=0.019lnn+0.31 (R2=0.991,P<0.001)

(2)

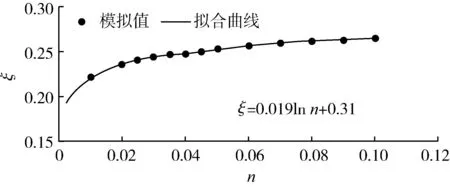
图3 支汊分流比与河道糙率关系

模拟时糙率取值范围为0.01～0.10，分流比变化范围为0.224～0.265。糙率在0.010～0.025期间时，分流比增长速率最快，从0.224增长到0.238，涨幅为1.4%；糙率在0.07～0.10期间时，分流比增长速率最慢，从0.261增长到0.265，涨幅为0.4%。糙率在0.025～0.070期间时，即平原河网糙率实际取值区间，分流比范围为0.238～0.261。总体而言，分流比随着糙率的增大而增大，增长速度逐渐变缓，但是总体变化范围不大，仅为4.1%。

平原河网糙率范围约为0.025～0.070[24]。在天然河道，河槽清洁、顺直、平滑、无沙滩、无滩的情形下，糙率取到最小值0.025。随着河槽植物、滩坑、石头的增多，糙率逐渐增大，在多滞流间段、多丛、有滩坑的情形下，平原河网糙率取到最大值0.070。在平原河网糙率取值范围内，分流比仅变化2.3%，可见糙率对分流比的影响很小。糙率对分流比的影响，主要是通过对水流不同程度的阻碍作用使过流流量发生变化来实现的。在河道断面形态及面积一定的条件下，糙率增大时水流流速明显降低，水流克服自身惯性转向所需离心力将相应减小，水流更易进入支汊，从而使分流比增大。陈界仁等[25]对赣江尾闾进行研究，发现植被较多、糙率较大的区域，支汊分流比有微弱增大的现象。但水中植物对糙率的影响程度小于0.05[26]，对分流比的影响小于1%，可以忽略不计。在平原河网整治工程中，常采用生态工程来净化水质[27]。由于糙率对分流比影响较小，在预测平原河网分流比或建立平原河网模型时，建议对分流量较大的主要支流的糙率进行测量，而对一些分流量较小的支流糙率可根据经验公式法推求或参考往年数据即可。

2.2.2分汊角度的影响

图4为谷渎港入口分流比ξ与分汊角度θ关系图。运用回归分析法建立了ξ与θ的相关关系式：

ξ=-0.090 57|sin(4θ)|+0.298 6 (R2=0.787)

(3)

图4 支汊分流比与分汊角度关系

分汊角度取值范围为10°～90°，分流比与分汊角度是复杂的三角函数关系。总体而言，θ在22.5°和67.5°时，分流比取极小值0.2；θ在45°时，分流比取极大值0.3。

目前对支汊分流比和分汊角度的关系尚无定论，如Grace等[28]在室内水槽试验中发现分汊角度在70°左右时，支汊分流比取最小值；童朝峰[4]计算了30°、60°、90°时的分汊流运动结构，得出分流比先减小后增大，在60°时分流比最小的结论。但是大多数研究者认为分汊角度增大时，河道水流系统为达到平衡状态会不断调整河道分流形势使支汊分流比减小[3,29-31]。本文采用小角度间隔10°进行研究，以更加全面地模拟分汊角度变化对分流比的影响，结果发现分流比和分汊角度的关系十分复杂：①分汊角度与分流比的关系不呈明显的正相关或负相关，而是复杂的三角函数关系；②分汊角度每变化10°，对分流比的影响在0.005～0.07之间，河道分汊角度测量误差约±3°，对分流比影响小于2%，可以忽略不计。就平原河网而言，不同角度所导致的变化可以归纳为：分汊角度在22.5°和67.5°时，支汊分流比最小；45°时，支汊分流比最大。因此，洪水期平原河网分汊河道行洪的过程中，要想提高主汊过洪能力，使相同洪水流量下，增大主汊承担的过洪量，降低支汊分流比，可在平原河网整治工程中设计分汊角度为60°～70°，使支汊分流比取最小值。在现实情况中，分流比和分汊角度的响应关系更为复杂，分汊角度变化会造成泥沙堆积并对地形等方面产生影响。分流比与分汊角度复杂的相关关系，可能是受到上层水体流向和底层流流向不一致的影响[4]，即底层流流向的偏转比表层流大，这在二维模型中被忽略了。

2.2.3支汊过水宽度比的影响

图5为谷渎港入口分流比ξ与支汊过水宽度比B关系图。运用回归分析法建立了ξ与B的相关关系式：

ξ=0.372B-0.017 (R2=0.998,P<0.001)

(4)

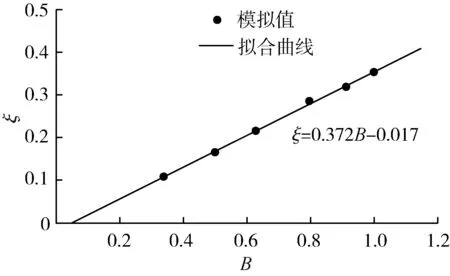
图5 支汊分流比与支汊过水宽度比关系

图5表明，在主汊宽度不变的情况下，支汊分流比与支汊过水宽度比呈良好的线性关系。支汊过水宽度比在0.34～0.63时,分流比由0.122增长至0.219。支汊过水宽度比在0.63～0.91时，分流比由0.219增长至0.321支汊过水宽度比在0.19～1时，分流比由0.321增长至0.35。总体而言，支汊过水宽度比对分流比影响较大，在支汊过水宽度比从0.34增长至1时，分流比由0.122增长至0.35。

随着支汊过水宽度比的增大，支汊过水宽度增大，支汊过水面积增大，从而过水能力提高，其分流比显著增大。在平原河网地区，地形冲淤引起的深度变化较小，过水断面的变化主要来自宽度的改变。相关研究[32-33]与本文的结论一致。Ramamurthy等[34]在室内直角明渠水槽试验中，保持其他条件不变，设置0.22、0.77、1这3种不同的过水宽度比，发现支汊过水宽度比为1时支汊分流比最大。可见，支汊过水宽度比越大，过水能力越强，支汊分流比越大。实际工程中，拓宽、填埋河道导致河道宽度的变化而直接影响了分流比。在对平原河网进行治理时，可考虑拓宽支汊河道，从而增大分流量，加快水体流动速度，起到改善内河水动力条件的效果。

2.3 河道的水体功能性连通参数对分流比的影响

2.3.1干流流量的影响

图6为谷渎港入口分汊河道分流比ξ与干流流量Q关系图。运用回归分析方法建立了ξ与Q的相关关系式：

ξ=0.452Q-0.252(R2=0.916,P<0.001)

(5)

图6 支汊分流比与干流流量关系

图6表明，随着干流流量的不断增加，支汊分流比逐渐减小，干流流量在8～20 m3/s时，分流比由0.28减小到0.2。在干流流量达到临界流量20 m3/s之后(20～30 m3/s时)，流量的增加对分流比几乎没有影响。

本文依据2018年10月26—27日实测流量，将研究的Y型河道流量变量参数值确定为8～30 m3/s。流量变化会引起分流段水深、流速、分水断面宽度以及过水断面面积等多个水力条件的改变，进而对支汊分流特性产生影响。在其他条件不变的情况下，干流流量增加，流速增大，水流克服自身惯性转向所需离心力相应增大，水流进入支汊变得困难，从而使分流比减小。不同区域河道乃至不同河段的分流比对流量变化敏感性都不同，甚至有不止一个临界流量产生[35-37]。总体来说，干流流量小于临界流量时，支汊分流比随着流量增大而减小；在干流流量达到临界流量后，流量增加对分流比几乎没有影响。在调水引流工程中，常常通过增大引水量提升整个河网的水动力条件。但需要指出的是，增大干流引水量会导致支汊分流比减小，可能对支汊水动力起到相反的效果。

2.3.2水位差的影响

图7为谷渎港入口分流比ξ与水位差(支汊与主汊水位之差)Δz关系图。运用回归分析法建立了分汊口分流比与水位差关系式：

ξ=0.718Δz+0.146 (R2=0.997,P<0.001)

(6)

图7 支汊分流比与水位差关系

图7表明，分流比与水位差呈良好的线性关系。水位差由0增大到0.45 m时，分流比由0.136增长到0.46。随着支汊水位降低，水位差增大，分流比也相应增大。

在主汊水位不变的情况下，水位差增大，支汊水位降低。受重力作用，水流有向水位较低的方向即支汊方向流动的趋势，导致分流比增大。分流比与水位差的线性关系在其他平原河网地区如长江江都段[38]、鄱阳湖[39]也得到了验证。在调水引流工程中，主支汊水位差是影响水量分配的重要因素。水位差越大，支汊流量越大，流速越快，支汊水体流动性越强。但是过大的水位差可能会导致开闸时支汊分流量突然增大，水位快速上涨而影响河道生态。因此，应充分考虑水位差对于分汊河道分流比的影响，采取闸坝联合调度、生态补水等措施，合理安排闸坝下泄水量。

2.4 多因素平原河网分流比综合预测方程

2.4.1预测方程

运用单因素logistic回归和多元回归并结合岭回归，得到多参数的平原河网分流比预测方程。过程如下：①选择ξ作为因变量，Q、n、θ、B、Δz作为自变量，在单因素回归的基础上，对各自变量进行如下变换，得到：x1=Q-0.252，x2=lnn，x3=|sin(4θ)|，x4=B，x5=Δz。以使得ξ对x1、x2、x3、x4、x5均为线性关系，这样可以使ξ对x1、x2、x3、x4、x5作多元回归。②随机选取80%的模拟后的数据进行多元回归。进行多元回归后，变换后的x1、x2、x3、x4、x5之间可能具有多重共线性，这样造成糙率n的P值为0.501，无法通过检验。③其余自变量均为P值极小、R2较大的情况下，选择岭回归并结合岭迹图，取岭参数k=0.6，进行岭回归，由此得到岭回归方程(式(7))。④将剩余20%数据代入式(7)进行验证，得到计算值与模拟值的比较结果。如图8所示。图8中计算值与模拟值接近，表明式(7)回归效果良好。该方程既克服了多重共线性，同时拟合效果良好，可用来预测平原河网分汊河道分流比。

(7)

图8 分流比实测值与计算值比较

2.4.2贡献模型

为进一步探究干流流量Q、糙率n、分汊角度θ、支汊过水宽度比B、水位差Δz对分流比ξ的贡献，首先以均值对各自变量进行标准化处理，然后按照上述过程进行岭回归，得到回归方程：

ξ=0.133Q-0.252-0.035lnn-0.0316|sin(4θ)|+0.14B+0.054Δz+0.255

(8)

变量标准化后，其自变量系数反映了它们对于分流比的贡献大小，与上文中定性讨论结果一致。式(8)中流量与支汊过水宽度比的系数分别为0.133和0.14，显著大于糙率、分汊角度、水位差的系数，表明支汊过水宽度比和干流流量是影响分流比的主要因素，各因素对于分流比的影响程度从大到小排序如下：支汊过水宽度比、干流流量、水位差、糙率、分汊角度。分析其原因，河道流量的大小很大程度上取决于河道过水面积和水流流速，而过水面积和水流流速与过水宽度比和干流流量直接相关。因此，在生态引流、改善内河水动力条件和防洪布局时，应主要注意支汊过水宽度比和干流流量的影响。