变截面旋转裂纹梁横向振动特性的研究
2019-07-09韩伟毛崎波田文昊
韩伟,毛崎波,田文昊
(南昌航空大学 飞行器工程学院,南昌 330063)
0 引 言
在航空工程中,有很多梁结构处于旋转运动状态,如螺旋桨、涡轮叶片等。这些结构在复杂恶劣的自然环境中长期处于高强度、高负荷运行状态,容易出现裂纹损伤。因此,对这些结构进行健康监测十分必要,以振动测试技术为代表的无损检测技术具有实时、高效、环境适应性强等优点,逐渐引起了国内外众多学者的广泛关注[1-4]。而对损伤结构进行动力特性分析是进行无损检测的重要基础。目前大部分研究主要集中在非旋转损伤梁结构的动力特性的研究,如大跨度桥梁、桥式起重机等,而对于螺旋桨、涡轮叶片等旋转梁的裂纹损伤动力特性的研究,至今只有少量文献涉及。
Liu C等[5]提出了一种裂纹六面体有限元法,用于裂纹叶片的动态分析,解决转子系统叶片裂纹建模精度与效率之间的矛盾。乔社宁等[6]通过搭建风机在自由悬挂状态下的试验模态分析平台,分别在无裂纹和不同裂纹深度等8种情况下对叶片振动特性进行了试验研究。研究结果表明:离心式风机叶轮结构固有频率随裂纹深度的增加而单调下降,裂纹越深,固有频率下降越快。范博楠等[7]研究了叶盘叶片进气及出气边产生的横向贯穿型裂纹的分布位置及深度变化对叶片一阶弯曲振动特性的影响,结果发现:当叶片进气或出气边位置阈值内出现裂纹及扩展时,一阶弯曲振动频率会小于正常值,此时叶片的一阶弯曲共振区域会增大。蒋宪宏等[8]对具有刚柔耦合效应的带裂纹旋转柔性梁进行建模和动力学特性分析研究,结果发现:裂纹梁的固有频率与裂纹处的弯矩正相关。J.W.Lee等[9]基于局部柔度模型模拟裂纹效应,用幂级数法结合传递矩阵法求解了含裂纹旋转梁振动特性,并讨论了转速与损伤程度对梁结构振动特性的联合影响机理。但是上述方法主要是针对等截面梁,且过程较为繁琐,计算程序复杂。
本文采用Frobenius方法将文献[9]等截面梁模型推广到高度和宽度均可按任意比例线型变化的梁体,提出一种求解变截面旋转裂纹梁横向振动特性的新方法,并通过数值算例验证该方法的有效性以及文献[9]中的结论,此外还研究裂纹位置和深度对振动特性的影响。
1 含裂纹梁局部柔度模型
以旋转悬臂梁为基础建立裂纹梁局部柔度模型,如图1所示。梁上含有n个开口裂纹,第i个裂纹距梁固定端的距离为xi,深度为hi,由文献[10]可知,裂纹可用无质量扭转弹簧模拟。
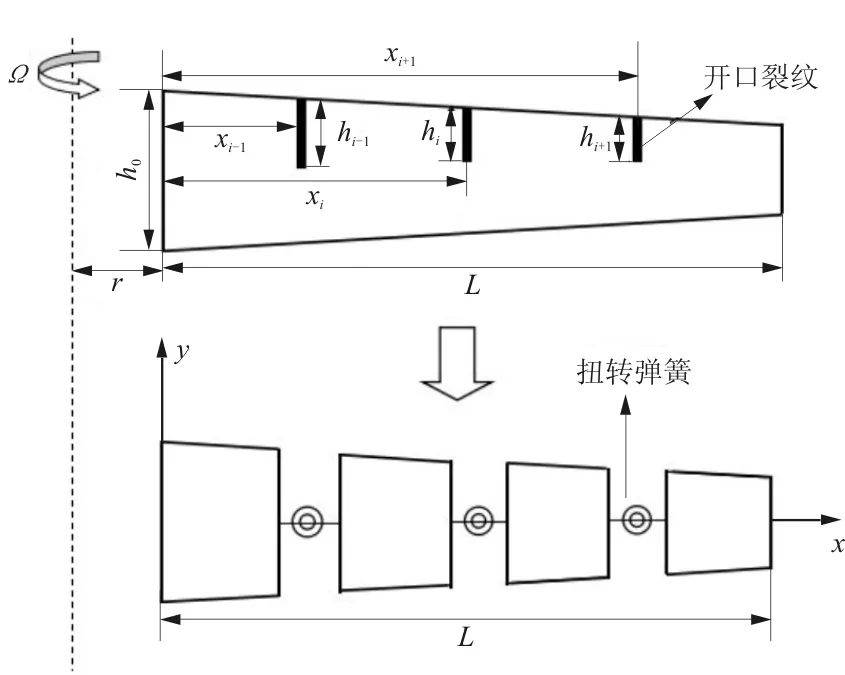
图1 含裂纹旋转梁局部柔度模型
梁的长度为L,梁的密度和弹性模量分别为ρ、E,转轴半径为r,转速为Ω,梁截面为矩形,其高度h(x)和宽度b(x)沿x轴方向减小,可以表示为
(1)
(2)
式中:h0和b0分别为梁固定端截面的高度和宽度;ch和cb分别为高度和宽度的渐变系数;当cb,ch均为0时,为均匀梁。
基于欧拉-伯努利梁理论,第i段完整梁的横向自由振动微分方程[11]为
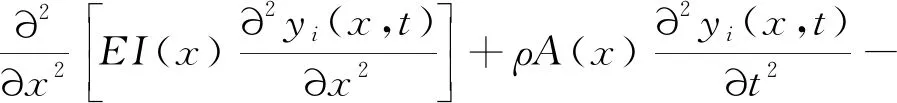
(3)
x∈[xi-1,xi],A(x)和I(x)分别是横截面积和惯性矩,T(x)是旋转梁所受离心力,可表示为
A(x)=b(x)h(x)
(4)
(5)

(6)
2 梁振动方程的Frobenius方法解
根据振动分析理论可知,梁的横向位移函数可分离为空间函数和时间函数,即方程(3)的解具有如下形式:
w(x,t)=φ(x)eiωt
(7)
将式(7)代入式(3)进行变量分离并将变量无量纲化,可得

(8)

根据Frobenius方法[12],第i段完整梁的自由振动位移可以表示为
Φi(X)=N1iF1(X)+N2iF2(X)+N3iF3(X)+
N4iF4(X)
(9)
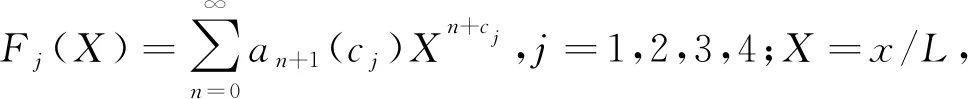
裂纹梁边界条件为
(10)
(11)
由文献[10]可知,在第i条裂纹处连续性条件为
(12)
式中:Xi为裂纹相对位置,Xi=xi/L。θi为梁的第i条裂纹引起的无量纲柔度[13]。
θi=5.346h0·J(si)
(13)
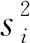
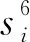

(14)
式中:si为相对裂纹深度,si=hi/h0。
由于式(13)中的无量纲柔度θi为J(si)和固定端截面高度h0的函数,因此必须给定梁的固定端截面高度h0才能得到无量纲柔度θi。
联合边界条件、裂纹处连续性条件、质量块处连续性条件可以得到由4(n+1)个方程组成的齐次线型方程组:
K(λ)N=0
(15)
式中:
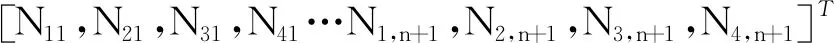
|K(λ)|=0
(16)
由式(16)可解出无量纲固有频率λ。
3 数值模拟
3.1 方法有效性验证
为了验证本文方法的有效性,以图1所示的旋转裂纹梁为研究对象,设置其弹性模量E=200 GPa,密度ρ=7 850 kg/m3,转轴半径r=0 mm,梁长L=800 mm,转速Ω=300 rad/s,固定端截面宽度b0=30 mm,高度h0=10 mm,相对裂纹深度s=0.5,宽度渐变系数cb=0,高度渐变系数cb=0~0.8,采用本文方法计算得到裂纹位于Xc=0.2,0.4,0.8三种工况下的前四阶固有频率,并将结果与文献[9]进行比对。文献[9]仅给出了等截面梁的结果,包含在本文的结果中。因之前在Frobenius方法的计算推导过程中对振动控制方程进行了无量纲化处理,使得关于旋转梁的各参数(转速Ω、转轴半径等r)无量纲化,而文献[9]中的各参数均是有量纲的,故需先对文献[9]中的各参数(转速Ω、转轴半径r)进行无量纲化处理得到无量纲化的各参数(转速U、转轴半径R),再运用本文方法计算得到无量纲化的固有频率λ,然后将无量纲固有频率有量纲化。
裂纹位于Xc=0.2,0.4,0.8三种工况下的前四阶固有频率如表1~表3所示,可以看出:采用本文方法计算得到的前四阶固有频率与文献[9]中的结果匹配良好;随着高度渐变系数的增加,一阶固有频率呈现递增趋势,而其他三阶频率均呈现下降趋势。这是因为影响变截面梁基频的主要因素为其根部的质量比重,而影响较高阶频率的主要因素为梁的平均柔度。

表1 含裂纹旋转梁前四阶固有频率(Xc=0.2,x=0.5)

表2 含裂纹旋转梁前四阶固有频率(Xc=0.4,x=0.5)
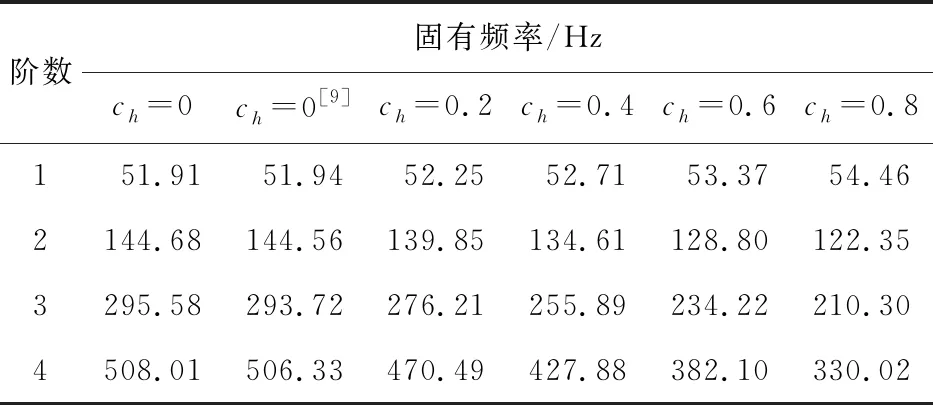
表3 含裂纹旋转梁前四阶固有频率(Xc=0.8,x=0.5)
3.2 裂纹位置和深度对梁振动频率的影响分析
为了进一步研究开口裂纹损伤对变截面旋转梁振动频率的影响,设置无量纲转速U=3,无量纲转轴半径R=1,厚度h0=0.02 m,宽度渐变系数cb=0.3,高度渐变系数ch=0.5,裂纹相对位置Xc在固定端和自由端之间移动,相对裂纹深度s=0,0.1,0.2,0.4,前三阶无量纲固有频率随裂纹位置和深度的变化情况如图2~图4所示。
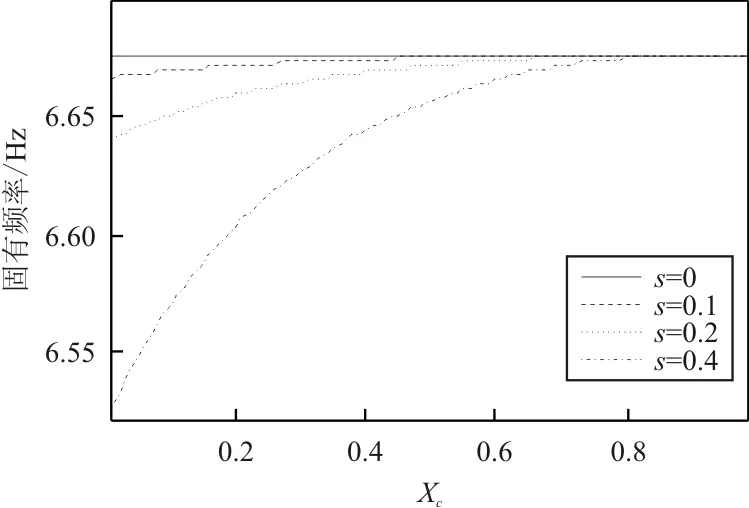
图2 一阶固有频率变化

图3 二阶固有频率变化
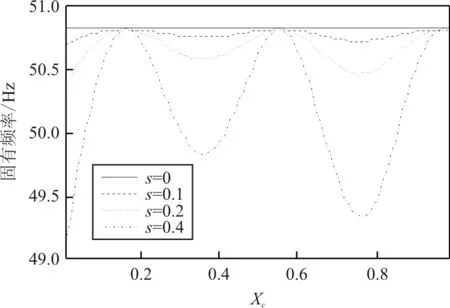
图4 三阶固有频率变化
从图2~图4可以看出:随着裂纹深度的增加,梁的前三阶固有频率均有逐渐减小的趋势,当裂纹位于固定端附近时,对固有频率的影响最大,对于第一阶固有频率,当裂纹向自由端移动时,裂纹损伤对其影响逐渐减弱,当裂纹移动至接近Xc=0.8时,梁的固有频率几乎不再变化;对于第二阶固有频率,当裂纹位于Xc=0.25,0.95附近时,无论裂纹深度如何变化,均不会对其造成影响,即为无效损伤位置;对于第三阶频率,当裂纹位于Xc=0.15,0.55,0.95附近时,为无效损伤位置。
3.3 损伤程度和转速对梁振动频率的联合影响分析
下面讨论损伤程度和转速同时变化时前两阶固有频率的变化情况。以钢制矩形变截面单裂纹悬臂梁为算例,设定弹性模量E=200 GPa,密度ρ=785 0 kg/m3,梁长L=1 m,固定端截面宽度b0=0.1 m,高度h0=0.1 m,转轴半径r=0.5 m,宽度渐变系数cb=0.1,高度渐变系数ch=0.3,梁的转速n在0~10 000 rpm之间渐变,相对裂纹深度s在0~0.5之间渐变。由前述分析可知,当裂纹位于固定端附近时,前两阶固有频率均出现最大衰减,为了体现裂纹损伤的影响,在数值计算中,设置裂纹相对位置为Xc=0.05。计算得到转速和相对裂纹深度连续变化时梁的前两阶固有频率,结果分别如图5~图6所示,可以看出:随着裂纹加深,前两阶固有频率均出现相应的衰减,但是随着转速增加,裂纹损伤所导致的频率衰减程度有逐渐减小的趋势;转速的增加使得梁的前两阶固有频率增大,并且随着裂纹加深,这种由转速提升引起的固有频率提升有逐渐增大的趋势。由此可见,损伤程度和转速对梁的前两阶固有频率具有明显的叠加作用效果。

图5 一阶固有频率变化
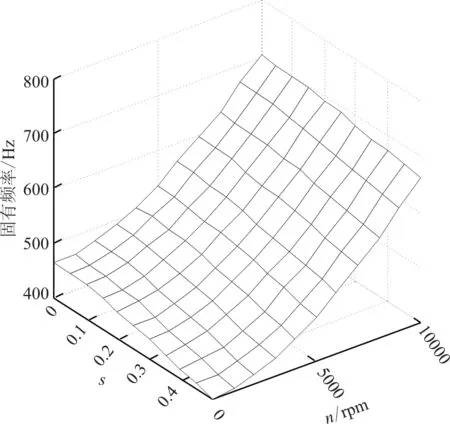
图6 二阶固有频率变化
为了进一步量化这种叠加作用效果,设不同裂纹深度所对应的前两阶固有频率分别为f1s和f2s,不同旋转速度所对应的前两阶固有频率分别为f1n和f2n,计算不同裂纹深度下转速变化引起的前两阶固有频率比f1n/f1和f2n/f2以及不同转速下裂纹深度变化引起的前两阶固有频率比f1s/f1和f2s/f2,结果如表4~表5所示。

表4 转速变化引起的一阶和二阶固有频率比值

表5 裂纹深度变化引起的一阶和二阶固有频率比值
从表4可以看出:随着转速的逐渐提升,一阶固有频率比值逐渐增大;但是当梁发生裂纹损伤后,这种由旋转效应引起的固有频率提升随相对裂纹深度的增加而变得更加显著。当相对裂纹深度s=0时,f1n/f1由转速n=2 000 rpm时的113.99%提升为转速n=10 000 rpm时的286.31%,当相对裂纹深度s=0.5时,f1n/f1由转速n=2 000 rpm时的122.48%提升为转速n=10 000 rpm时的365.71%。
从表5可以看出:随着相对裂纹深度逐渐加深,一阶频率衰减量逐渐增大;但是当梁旋转后,这种由裂纹损伤引起的频率衰减幅度随转速的提升有逐渐减小的趋势。当转速n=0时,f1s/f1由裂纹深度s=0.1时的98.75%下降至裂纹深度s=0.5时的74.52%,当转速n=10 000 rpm时,f1s/f1由裂纹深度s=0.1时的99.65%下降至裂纹深度s=0.5时的95.19%。
通过观察表4和表5的二阶固有频率比值发现转速和损伤程度与前两阶固有频率比值均有同样的耦合作用效应。但相比之下,这种耦合作用效应对一阶固有频率比值的影响更为显著。
上述分析所得出的结论和文献[9]中的结论一致,从而进一步验证了文献[9]中的结论,并将该结论的适用范围从均匀梁拓展到了变截面梁。
4 结 论
(1) 对于变截面梁,随着高度渐变系数的增加,一阶固有频率呈现递增趋势,而其他三阶频率均呈现下降趋势。
(2) 当裂纹位于梁的固定端附近时,对固有频率的影响最大,前三阶固有频率分别包含一、二、三个无效损伤位置。
(3) 转速和损伤程度对前两阶固有频率比值均有耦合作用效应,相比之下这种耦合作用效应对一阶固有频率影响更为明显。该结论不仅适用于均匀梁,对变截面梁也同样适用。
