某型倾转旋翼机的旋翼桨叶气动优化设计
2019-07-09孙凯军张练付义伟于悦洋
孙凯军,张练,付义伟,于悦洋
(中国航天空气动力技术研究院 彩虹无人机科技有限公司,北京 100074)
0 引 言
倾转旋翼机的概念早在20世纪40年代初由贝尔公司提出,自20世纪50年代开始,美国先后研制了XV-3,XV-15等[1]具有技术验证性质的倾转旋翼机。XV-15的飞行试验取得了较好效果,引起美国军方的关注。贝尔公司在XV-15的基础上,联合波音公司成功研制了V-22倾转旋翼机[2-3]。V-22被美国军方大量采购,并投入实战,实现了倾转旋翼飞行器的实际应用。20世纪80年代末,美国开始无人倾转旋翼的研制,贝尔公司在1988年研制了“瞄准手”无人倾转旋翼机并进行首飞,之后在其基础上研制了“鹰眼”无人倾转旋翼机。“鹰眼”在1998年3月正式试飞,并于2003年被美国海岸警卫队选用。
倾转旋翼飞行器通过转换旋翼功能实现高速飞行,即利用倾转机构实现其主要气动部件在旋翼与螺旋桨之间转换,实现垂直飞行时以直升机模式飞行,高速时以螺旋桨飞机模式前飞,从而兼顾低速与高速飞行性能。由此可见,倾转旋翼桨叶的气动设计要综合考虑直升机旋翼和固定翼的不同工作模式对其的不同要求,也就是直升机旋翼和固定翼螺旋桨两种气动外形的折中。
在常规旋翼气动特性分析和桨叶外形优化设计方面,早期的数值分析方法[4-5]主要采用动量叶素理论或涡尾迹方法。近期,H.Yeo等[6]基于均匀入流假设,采用升力线理论结合多学科优化方法开展倾转旋翼优化设计。C.W.Stahlhut等[7]在对倾转旋翼进行参数化分析及优化设计研究过程中,采用动量叶素理论分析了不同桨叶构型对倾转旋翼性能的影响。这些方法虽然可以高效地计算旋翼的气动性能,但是不能满足外形较复杂、精度要求较高的旋翼气动设计要求。
随着近些年计算机发展水平的不断提高,CFD方法已经引入到旋翼的气动外形设计之中。国外A.LePape等[8]通过耦合CFD方法和梯度方法的优化策略,开展悬停状态下旋翼平面外形优化设计。M.A.Potsdam等[9]基于嵌套网格和RANS方程,较好地预测了悬停状态下倾转旋翼的气动性能,但未能开展优化设计研究。李鹏等[10-11]采用CFD方法对倾转旋翼/机翼气动干扰进行数值模拟,但未进一步开展旋翼桨叶优化设计。
综合国内外研究现状发现,已经开展的工作主要针对常规直升机旋翼平面形状、翼型等展开分析研究,但是对倾转旋翼桨叶平面形状的优化设计相对较少,同时CFD和风洞试验在该方面的应用也相对较少。
本文采用基于Kriging模型的优化方法,结合动量理论[12]进行倾转旋翼机的旋翼桨叶多目标气动优化设计。对优化设计结果进行非定常数值模拟验证,并且开展缩比旋翼风洞试验,进一步验证优化设计和数值模拟方法。
1 气动特性数值预测方法
1.1 控制方程和数值方法
积分形式的三维雷诺平均N-S方程可以写成如下守恒形式:
(1)
式中:Q=(ρ,ρu,ρv,ρw,ρe)T为守恒变量;∂V为某一固定区域V的边界;n为边界的外法向矢量;Fc为对流矢通量;Fν为粘性矢通量。
采用有限体积法求解上述控制方程,时间推进采用LU-SGS 隐式格式。采用全湍流假设,湍流模型采用S-A方程模型。物面边界条件采用无滑移绝热壁面条件。
1.2 嵌套网格技术
网格技术是计算流体力学的基础,本文对旋翼桨叶粘性绕流的数值模拟采用嵌套网格技术。嵌套网格自J.A.Benek等[13]于1985年提出以来,得到广泛应用并快速发展。它有效地解决了模拟复杂外形或复杂流动中单块结构化网格生成困难和质量差的问题。国内外研究人员将嵌套网格技术运用于二维翼型、三维带副翼、襟翼的机翼以及全机等复杂外形的流动数值模拟,极大地推动了嵌套网格技术的发展和应用。在处理具有相对运动的物体时,利用运动嵌套网格技术,使嵌套网格在模拟复杂非定常流动中具有更加明显的优势。例如二维翼型的震荡运动、三维导弹投放以及旋翼的数值模拟等。
2 基于Kriging的多目标遗传算法
近年来,基于代理模型的优化技术(简称代理优化技术)由于其高效、实用的特点受到了越来越多的关注。代理优化技术是一种能够通过采用相对较少计算量的数学模型来描述和代替复杂,计算花费较大的试验或数值模拟。它的最大优点是通过建立近似模型来降低调用流场分析程序的次数,从而减少优化设计过程的计算时间。目前比较常用的近似模型主要有响应面模型,Kriging模型,径向基函数模型等,国内外科研人员在这些模型上均已开展了相应研究。Kriging代理模型[14-16]对高度非线性、多峰值函数具有很强的拟合能力,而大多数气动优化问题本身具有高度非线性特性,因此Kriging模型成为很好的选择。在利用优化算法进行寻优时,利用Kriging模型代替比较耗时的流场分析,可极大减少优化设计过程的时间,提高优化效率。
遗传算法不仅具有全局性优化的特点,而且鲁棒性、可靠性和可移植性好,所以遗传算法在工程优化中得到广泛应用。因此,本文采用此算法优化求解EI[17]最大值和Kriging模型的最小值,其中试验样本点由拉丁超立方抽样试验[18]得到。基于Kriging代理模型的优化设计流程如图1所示。
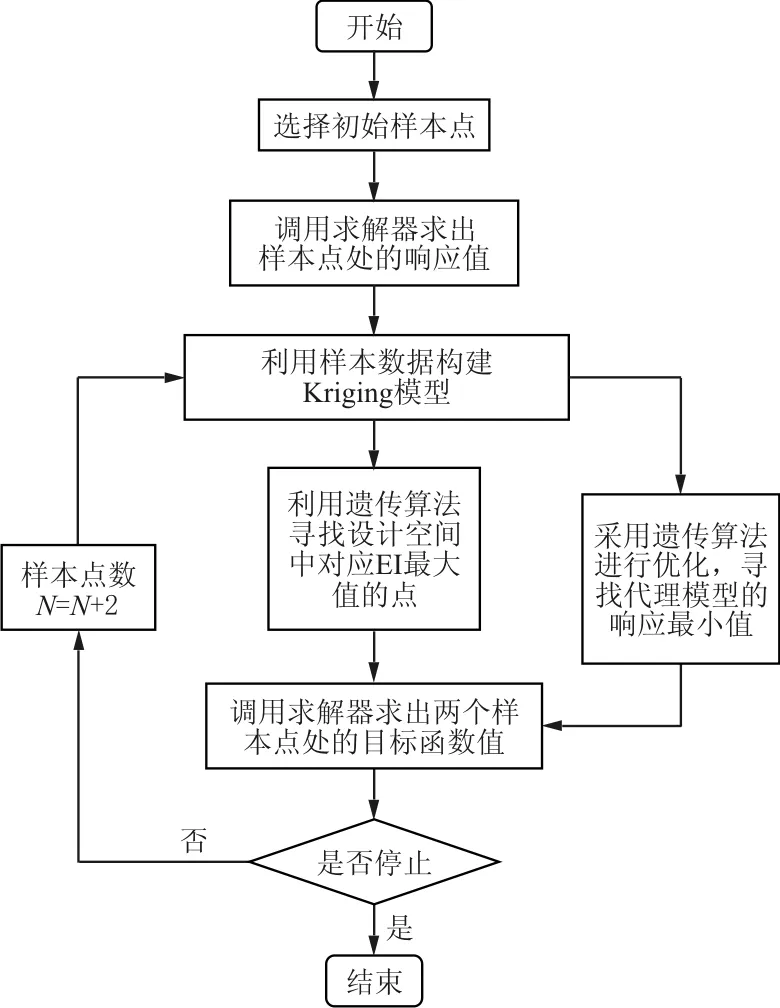
图1 优化设计流程图
3 旋翼桨叶优化设计
3.1 翼型选型
通过翼型选型对比以及优化设计,桨叶(沿径向0.2R~1.0R)主要采用两个翼型:xx1和xx1-mod,相对厚度分别为9.4%和12%。桨根位置采用翼型xx1-mod,桨尖位置采用翼型xx1,桨叶中间位置进行适当过渡,翼型如图2所示。
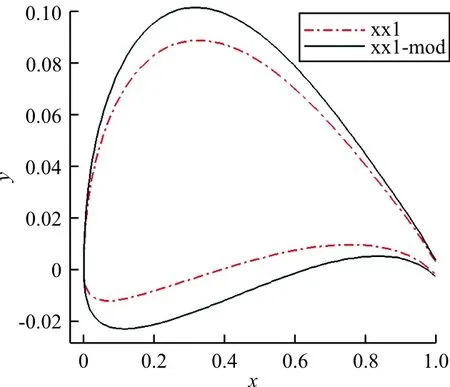
图2 旋翼桨叶翼型
3.2 旋翼平面形状优化设计
倾转旋翼两个主要状态是垂直起降和巡航前飞,垂直起降状态旋翼拉力承担整个倾转旋翼机的重量,而巡航前飞旋翼拉力只需克服倾转旋翼机的阻力,所以垂直起降状态的拉力是巡航前飞旋翼拉力的十几倍,造成两个状态下的旋翼性能差距过大,进而设计过程中要兼顾两者性能问题。
本文旋翼设计指标:
(1) 桨叶直径:3.2 m
(2) 桨叶数:2
(3) 垂直起降阶段
飞行高度: 0 km
飞行速度: 0 m/s
拉力: ≥ 2 352 N
功率: ≤ 37.7 kW
(4) 巡航前飞阶段
飞行高度: 2 km
飞行速度: 41.7 m/s
拉力: ≥147 N
效率: ≥60.0%
兼顾翼型最优性能和桨尖马赫数,此次优化设计中限制垂直起降状态转速1 000 rpm。本文采用CST[19-21]方法对旋翼桨叶的弦长C和扭角Beta进行参数化,同时将巡航前飞状态的转速Nc和总距角Theta作为设计变量引入到整个优化设计过程中。
本文采用基于Kriging的多目标遗传算法,结合动量理论(评估桨叶性能)进行倾转旋翼气动外形设计。
本文的优化问题可以表述为:
(1) 优化目标
垂直起降状态:旋翼桨叶拉力最大;
巡航前飞状态:旋翼桨叶效率最高。
(2) 设计变量
通过CST参数化方法,得到表征旋翼桨叶弦长C和扭角Beta的变量各7个,加上巡航前飞状态的转速Nc和总距角Theta,总共16个设计变量。
(3) 约束条件
垂直起降状态:旋翼桨叶功率≤37.7 kW;
巡航前飞状态:旋翼桨叶拉力≥147 N。
(4) 优化中止条件
遗传算法最大迭代次数≤500。
经过重复迭代设计,旋翼设计结果如表1~表4所示。表1为旋翼桨叶几何参数,表2为旋翼桨叶飞行状态参数,表3为旋翼桨叶0.2R~1.0R弦长和扭角分布,表4为旋翼气动性能动量理论评估结果。旋翼三维外形示意图如图3所示。
从表4的动量理论估算结果可以看出,悬停状态功率37.75 kW,拉力2 589.2 N,效率78.6%;巡航状态拉力219.3 kg,效率70.7%。设计结果满足要求,下一步需要进行CFD验证。

表1 旋翼桨叶几何参数

表2 旋翼飞行状态参数

表3 桨叶弦长扭角分布(悬停状态)
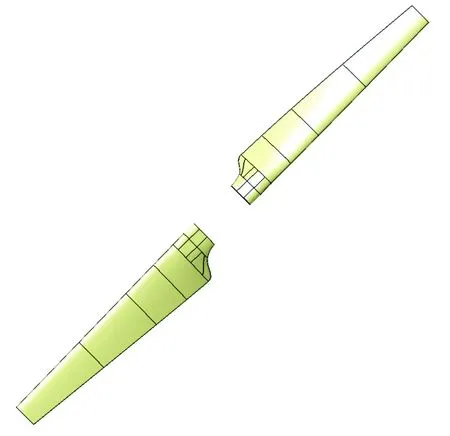
图3 旋翼设计结果
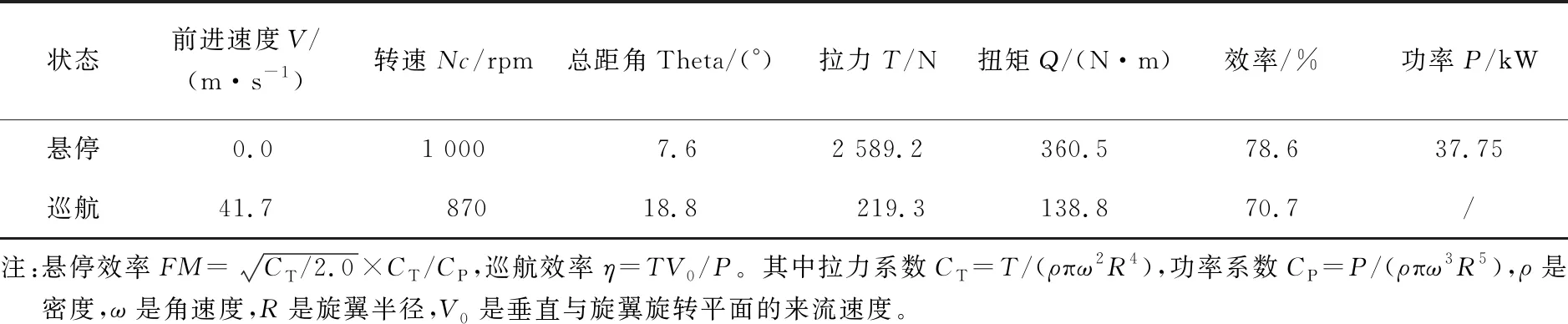
表4 桨叶性能结果(动量理论)
3.3 旋翼设计结果CFD验证
动量理论计算方法作为快速气动预测的手段,在旋翼气动设计过程中发挥重要作用。但是工程方法计算精度较低,不能满足外形复杂、精度要求较高的旋翼气动设计要求,所以需要对上述设计结果进行CFD校验。本文采用嵌套网格非定常方法对旋翼性能进行校核。
网格示意图如图4所示。
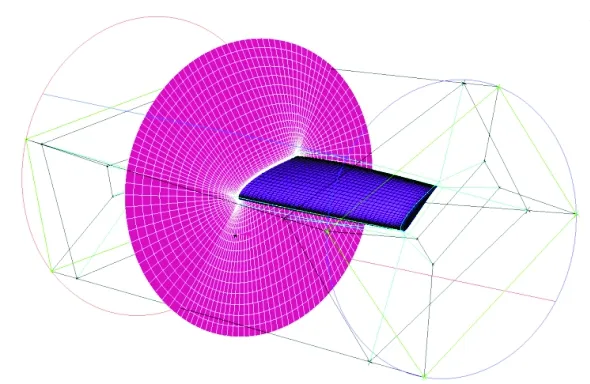
(a) 悬停状态

(b) 巡航状态
CFD流场图如图5所示,旋翼设计CFD校核结果如表5所示。

(b) 巡航状态涡量图

表5 旋翼设计CFD结果
从表5的数值模拟结果可以看出:悬停状态功率37.6 kW,拉力2 413.04 N,效率71.0%;巡航状态拉力233.23 N,效率63.1%。非定常数值模拟结果和动量理论估算的结果基本一致,旋翼设计结果满足设计指标,下一步进行风洞试验验证。
4 风洞试验验证
为了验证本文优化设计方法以及数值模拟的可靠性,进行缩比旋翼风洞试验。综合考虑试验环境和试验设备,本次试验模型为1∶2.5缩比模型(如图6所示),吹风试验风洞采用串置开口回流风洞(如图7所示)。旋翼试验台(如图7所示)净高3.1 m,可以俯仰偏转±10°,内部装有50 kW的直流电机,可无级变频调速,测力天平安装于顶部。
全尺寸旋翼设计点桨尖马赫数为0.5,雷诺数为1.8×106。马赫数大于0.4,需要考虑压缩性影响,在保证马赫数相似的条件下,缩比旋翼设计点转速为2 500 rpm,雷诺数为0.72×106,还不到低雷诺数范围。本次试验主要目的是验证数值模拟方法的可靠性,因此1∶2.5缩比模型可以满足本次风洞试验的需求。

图6 缩比旋翼

(a) 风洞模型

(b) 旋翼试验台
总距角5.6°,风速0 m/s悬停状态风洞试验与CFD结果对比如图8所示,总距角7.6°,风速0 m/s悬停状态风洞试验与CFD结果对比如图9所示。
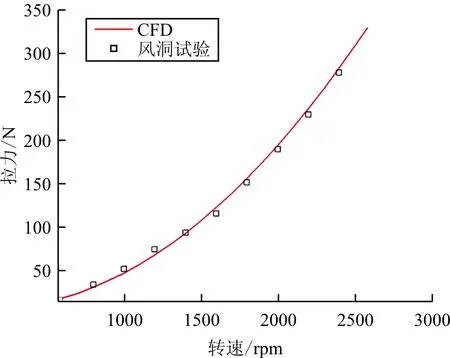
(a) 拉力随转速变化关系曲线
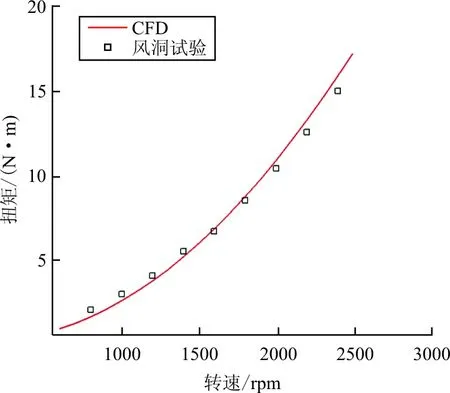
(b) 扭矩随转速变化关系曲线
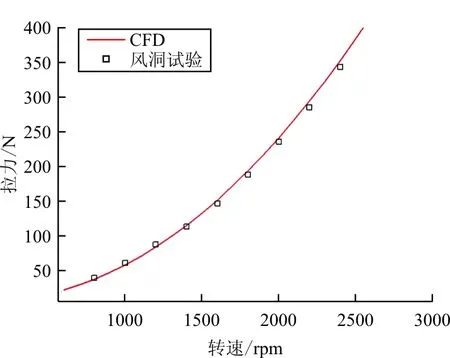
(a) 拉力随转速变化关系曲线
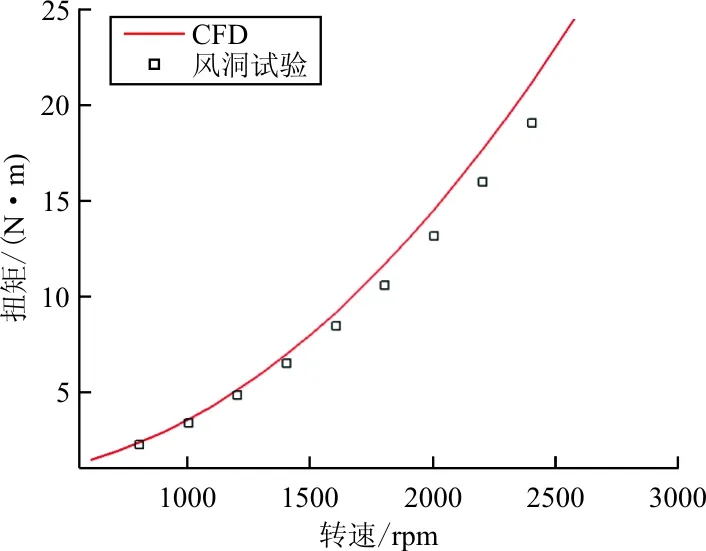
(b) 扭矩随转速变化关系曲线
从图8~图9对比可以看出:两者的拉力结果吻合的非常好。CFD扭矩结果略微偏大,这是因为CFD采用全湍计算,阻力预测偏保守,而旋翼翼型属于层流翼型,所以风洞试验中旋翼扭矩小于CFD结果。
旋翼倾转前飞状态风洞试验与CFD对比如图10所示,旋翼总距角7.6°,风速9 m/s,转速2 100 rpm。
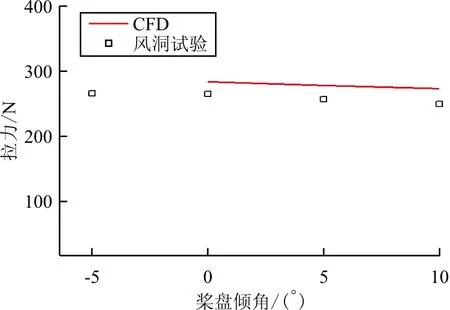
(a) 拉力随桨盘倾角变化关系曲线
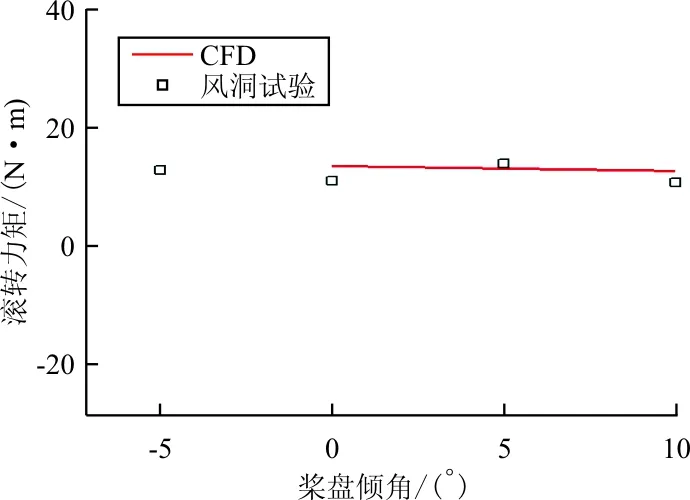
(b) 滚转力矩随桨盘倾角变化关系曲线
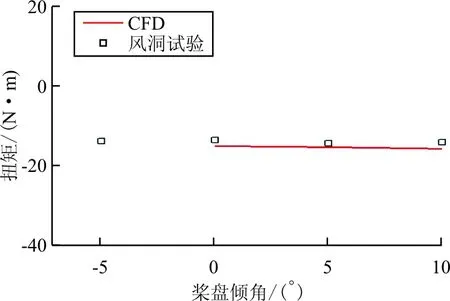
(c) 扭矩随桨盘倾角变化关系曲线
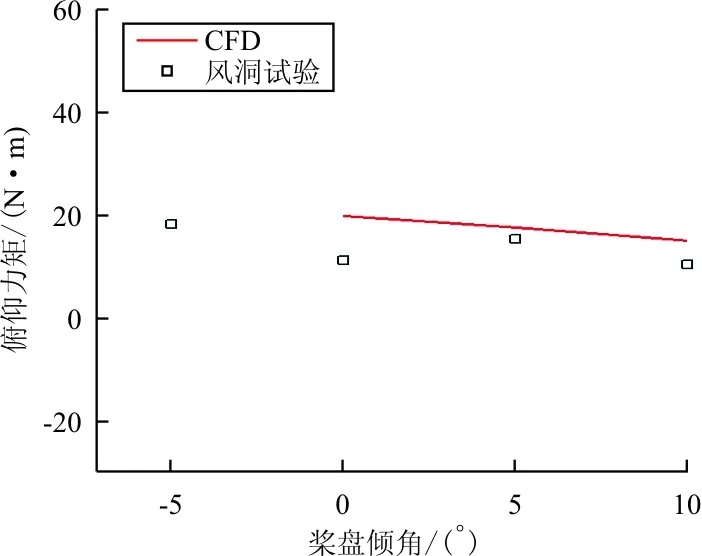
(d) 俯仰力矩随桨盘倾角变化关系曲线
从图10对比结果可以看出:拉力、滚转力矩、扭矩、俯仰力矩和CFD结果偏差都在5%以内,两者结果基本一致。
5 结 论
(1) 本文采用基于Kriging模型的多目标遗传算法,结合动量理论,开展倾转旋翼桨叶平面形状优化设计,非定常数值模拟结果和动量理论估算结果基本一致,旋翼设计结果满足设计要求。
(2) 倾转旋翼桨叶设计结果进行缩比旋翼试验,结果表明:拉力、滚转力矩、扭矩、俯仰力矩和CFD结果偏差都在5%以内。
