基于接触应力的高参数汽轮机叶片枞树形叶根型线优化

倪长辉 周显丁

摘要：为提高汽轮机叶片叶根型线的设计效率和产品质量，基于接触应力约束下的枞树形叶片叶根型线设计，将传统的基于经验的设计与经典优化理论相结合，推导适合叶根型线的设计方法。采用移动渐近线法（method of moving asymptotes， MMA）进行结构拓扑优化，以某低压末级动叶片设计为例，优化前、后叶根和轮槽的VON Mises应力对比表明，所推导的方法能够快速得到所需的型线设计。该设计使得叶根与轮槽间的接触应力降低，叶片的使用寿命提高。

关键词：汽轮机;叶根;型线;优化;接触应力

中图分类号：TK263.3

文献标志码：B

文章编号：1006-0871（2019）02-0047-05

0 引 言

汽轮机叶片是汽轮机的重要组成部件，是将热能转化为机械能的核心部件，可以说是汽轮机的心脏部件。为顺利、高效地将蒸汽能量转化为机械能，汽轮机叶片不仅需要有良好的气动性能和热动力性能，而且要具有足够的安全性。大功率汽轮机动叶片通常工作在高温高压的蒸汽或者湿蒸汽中，不仅受离心力、蒸汽弯力和蒸汽激振引起的交变力作用，还受到湿蒸汽腐蚀和水滴冲蚀作用等。随着汽轮机运行时间的增长，叶片可能出现蠕变、裂纹甚至断裂，带来毁灭性的后果。因此，汽轮机叶片的安全性能设计尤为重要。

汽轮机叶片由型线部分（工作部分）、叶根部分、叶顶部分和连接部分组成。型线部分的设计主要考虑气动特性（即经济性）和安全性要求，叶根部分主要考虑结构的安全性。叶根类型主要有倒T形（外包倒T形）、双倒T形（外包双倒T形）、叉形、枞树形和菌形等。枞树形叶根的承载能力大，常用于大功率汽轮机的低压末级和次末级动叶片中。枞树形叶根与轮槽连接在一起，其接触应力越小，结构的性能越好，所以好的叶根型线设计非常必要。通常，叶根型线设计先由经验丰富的设计师设计，然后进行数值仿真分析，对不满意的型线按仿真结果修改后重新分析，直到满意为止。这样的设计流程耗时耗力，且需要一定的经验，设计效率低下。

强度是结构设计中首先要考虑的问题。如果结构强度不能保证，那么关于结构的其他所有要求也就无须考虑。衡量強度最简单的方法是计算结构中的应力。过高的应力可能导致结构出现断裂、疲劳等破坏，因此考虑结构应力非常重要。BENDSE等[1]就应力优化问题的重要性进行详细的解释说明。历史上出现的几次大事故，如1954年英国客机坠毁事件、1979年美国DC-10飞机失事事故[2]、1988年波音737客机失事事故[3]和1980年挪威基亚兰德号海洋平台倾斜倾覆事故[4]等，都是由于结构的局部应力过大造成疲劳断裂失稳，从而导致整个结构破坏的。因此，越来越多的研究者研究应力优化问题。

考虑应力的优化设计已经趋于完善。STOLPE等[5]采用线性混合整数规划法求解应力约束下的轻量化拓扑优化。SVANBERG等[6]采用整数规划法进行应力约束问题求解，但是整数规划法解决大规模设计问题会因计算量庞大而效率低下。在国内，隋允康等[7]研究拓扑设计变量的独立连续映射关系，求解应力和位移作为约束的连续体结构拓扑优化。隋允康等[8]还采用ICM方法将应力约束转换为应变能约束，并且将大规模的应力约束进行凝聚。荣见华等[9]将独立连续映射方法与渐进化方法相结合，在每步迭代计算中不断更新位移和应力约束，提出一种新的应力优化方法。STEVEN等[10]采用渐进优化方法对柔度和应力的多目标优化问题进行研究。LI等[11]采用渐进优化方法增加和删除有限元单元，求解最小化最大应力问题。需要特别说明一点的是，在考虑应力的拓扑优化中存在应力的奇异性现象，目前公认的处理这类奇异性最有效的方法是GUO等[12]和CHENG等[13]提出的放松法。将应力的优化应用到汽轮机叶片叶根型线的设计中，能缩短设计时间，提高设计质量。

本文基于接触应力约束下的枞树形叶片叶根型线设计，将传统的基于经验的设计与经典优化理论相结合，推导适合叶根型线的设计方法，在提高设计效率的同时提高产品质量。

1 优化分析

1.1 叶根模型和优化方程

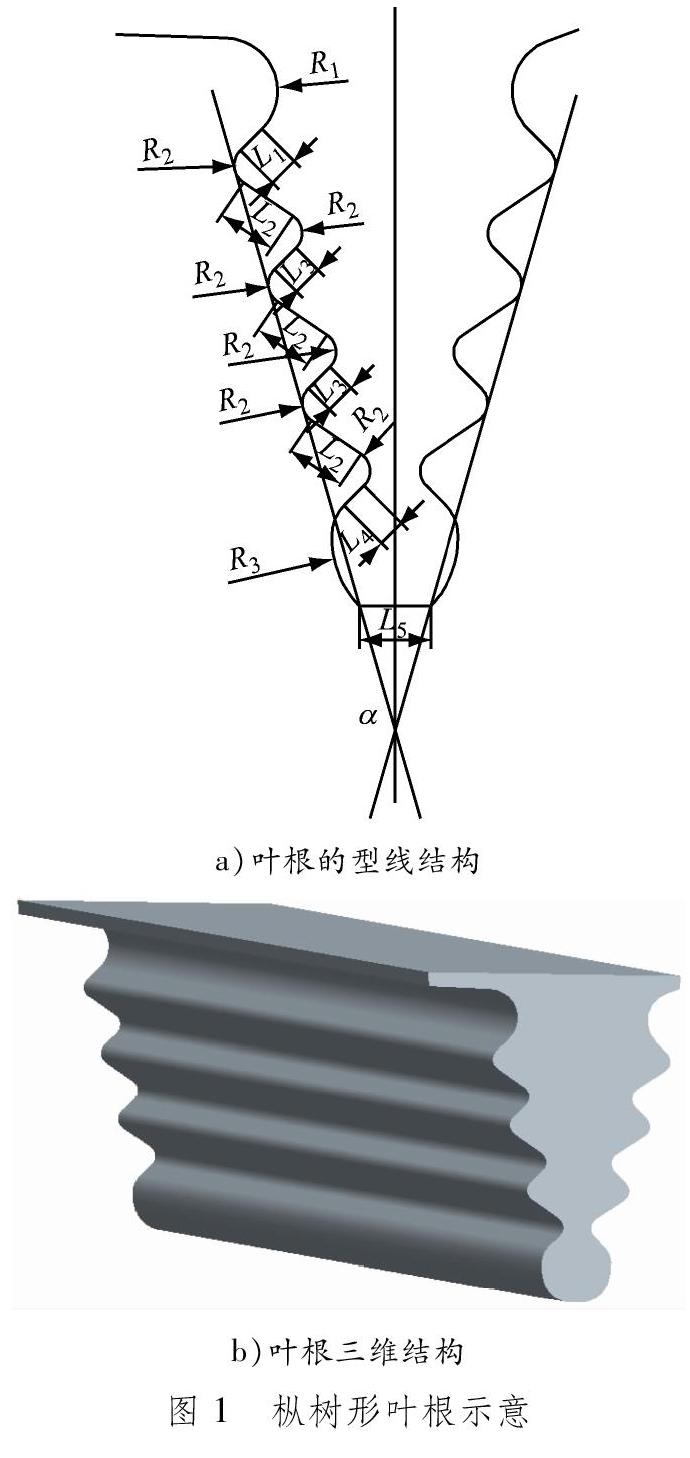
多齿枞树形叶根型线及其三维结构见图1。

在不同的设计中，叶根齿数稍有不同，图1为4齿枞树叶根。过渡圆角R1～R3、接触面宽度L1～L4和开口角度α为叶根的可设计参数，调节不同的参数可以得到满足设计要求的叶根型线。由于叶片工作时主要受离心力作用，已有的设计经验表明，R2、L1、L3和L4的影响最明显。

通常，多齿枞树形叶根有直齿叶根（沿轴线垂直装入）、斜齿叶根（沿与轴线成β角度方向装入）和圆弧齿叶根（沿圆弧方向和轴向装入）3种。选择直齿（即β=0）和斜齿叶根（即β>0）为研究对象，圆弧齿叶根修改设计参数后，本文方法同样适用。将叶根参数R1～R3、L1～L4、α和β总共9个参数作为设计变量，其优化函数为

1.2 优化模型的边界条件

由于叶轮结构具有高度的对称性，为减少计算量，分析单个叶片的旋转对称模型，见图2。叶根与轮槽的工作面通过离心力作用相互接触。整个模型采用三维8节点六面体单元进行计算，其网格模型见图3。分析模型由136 805个节点和211 901个单元组成。

叶根和轮槽材料参数见表1。叶根与轮槽的工作面采用面-面接触关系，在叶轮旋转对称面上施加对称边界条件，叶片转速设为3 000 r/min。

1.3 优化算法

由于结构拓扑优化的设计变量和约束较多，优化问题的计算规模很大，简单的求解方法不能满足需求。目前，结构拓扑优化求解方法有准则法（optimality criterion， OC）、数学规划法（mathematical programming， MP）和仿生类算法（遗传算法、神经网络算法、模拟退化算法和蚁群算法）等。本文采用移动渐近线法（method of moving asymptotes， MMA）[14]，其算法原理如下。

对于上述优化问题，采用MMA计算时，先引入人工变量改变每个子优化问题的形态，从而形成一系列凸子优化问题。子优化问题的数学表达式为

1.4 优化过程

结构分析采用MSC Marc，参数化优化模型采用Pro/Engineer建立，网格由ANSA定义生成，优化算法采用MMA，优化流程见图4。

2 优化结果

以某低压末级动叶片设计为例，使用上述方法进行优化，叶根与叶轮的应力降低50 MPa。优化结果对比见表2，其中初始结构是仅依据工程设计经验得到最佳结果。优化前、后叶根和轮槽的应力云图分别见图5和6。

由此可以看出，优化前、后的应力云图基本相同，最大应力区域在优化前、后未发生改变。仅依靠工程师经验降低叶根与轮槽间的应力耗时耗力，本文方法能够快速地降低叶根与轮槽间的接触应力，提高叶片的使用寿命，对产品的质量提高具有重要的作用。该叶根型线已成功应用到部分火电厂及核电厂百万机组的末级动叶片中。

3 结束语

对枞树形叶根型线进行三维优化设计，以叶根型线的几何尺寸和安装角度为设计变量，以轮槽接触面上的最大VON Mises应力作为目标函数，以结构柔度（其倒数即为结构的刚度）和叶根接触面上的最大VON Mises应力作为约束函数，通过优化降低初始结构叶根与轮槽的接触应力，使结构的性能得到提高。本文设计的叶根型线已应用到部分火电厂及核电厂百万机组的末级动叶片中，效果良好。

将设计域变为其他类型的叶根型线，在目标函数与约束函数相同的情况下，本文方法仍然适用。特别需要说明的是，采用本文方法进行优化设计时，由于约束函数中有接触应力存在，而接触应力对网格的质量要求很高，所以如果设计变量变化很大，相应的网格变化可能会带来接触应力的奇异现象。这种现象与普通的应力约束奇异现象[12-13]可能不同，需要进行更加深入的研究。

参考文献：

[1] BENDSE M P， SIGMUND O. Topology optimization：Theory， methods and applications[M]. Heidelberg：Springer-Verlag， 2004：1-20.

[2] WITHEY P A. Fatigue failure of DE Havilland comet I[J]. Engineering Failure Analysis， 1997， 4（2）：147-154. DOI：10.1016/S1350-6307（97）00005-8.

[3] SCHIJVE J. Fatigue of aircraft materials and structures[J]. International Journal of Fatigue， 1994， 16（1）：21-32. DOI：10.1016/0142-1123（94）90442-1.

[4] 王國周， 瞿履谦. 钢结构原理与设计[M]. 北京：清华大学出版社， 1993：1-20.

[5] STOLPE M， SVANBERG K. Modelling topology optimization problems as linear mixed 0-1 programs[J]. International Journal for Numerical Methods in Engineering， 2003， 57（5）：723-739.DOI：10.1002/nme.700.

[6] SVANBERG K， WERME M. Sequential integer programming methods for stress constrained topology optimization[J]. Structural and Multidisciplinary Optimization， 2007， 34（4）：277-299.DOI：10.1007/s00158-007-0118-2.

[7] 隋允康， 杨德庆， 王备. 多工况应力和位移约束下连续体结构拓扑优化[J]. 力学学报， 2000， 32（2）：171-179.

[8] 隋允康， 叶红玲， 彭细荣， 等. 连续体结构拓扑优化应力约束凝聚化的ICM方法[J]. 力学学报， 2007， 39（4）：554-563.

[9] 荣见华， 葛森， 邓果， 等. 基于位移和应力灵敏度的结构拓扑优化设计[J]. 力学学报， 2009， 41（4）：518-529.

[10] STEVEN G P， LI Q， XIE Y M. Multicriteria optimization that minimizes maximum stress and maximizes stiffness[J]. Computers & Structures， 2002， 80（27-30）：2433-2448.DOI：10.1016/s0045-7949（02）00235-3.

[11] LI Q， STEVEN G P， XIE Y M. Evolutionary structural optimization for stress minimization problems by discrete thickness design[J]. Computers & Structures， 2000， 78（6）：769-780. DOI：10.1016/S0045-7949（00）00057-2.

[12] GUO X， CHENG G D. A new approach for solution of singular optimum in structural topology optimization[J]. Acta Mechanica Sinica， 1997， 13（2）：171-178. DOI：10.1007/s00158-001-0156-0.

[13] CHENG G D， GUO X. ε-relaxed approach in structural topology optimization[J]. Structural and Multidisciplinary Optimization， 1997， 13（4）：258-266. DOI：10.1007/BF01197454.

[14] SVANBERG K. Method of moving asymptotes：A new method for structural optimization[J]. International Journal for Numerical Methods in Engineering， 1987， 24（2）：359-373. DOI：10.1002/nme.1620240207.

（编辑 武晓英）