基于有限元的太阳翼驱动机构结构强度分析验证

朱兴高 栾家辉 代永德

摘要：为研究空间驱动机构在力学和热学环境下的结构强度，提出一种强度分析验证方法。以太阳翼驱动机构为例，在随机振动载荷和热载荷作用下，研究机构强度设计是否满足要求。利用HyperWorks和Abaqus构建有限元模型，借助振动扫频试验数据完成模型的有效性验证，开展随机振动分析和热学分析，并对分析结果进行合理性判断。结果表明：应力强度最大值均在安全设计裕度内，太阳翼驱动机构结构强度满足设计要求。该验证方法可有效指导产品设计、降低研制费用和缩短研制周期。

关键词：太阳翼驱动机构;结构强度;模型验证;随机振动;热真空;热循环;有限元

中图分类号：V414.1

文献标志码：B

文章编号：1006-0871（2019）02-0011-04

0 引 言

航天器在发射和在轨运行过程中经历剧烈的振动环境和热学环境。随机振动激励来自于发动机的不稳定燃烧引起的推力脉动和相关设备的不平衡旋转导致的结构振动等。[1-2]热环境应力来自于空间外部热流和航天器自带的电机、导电环和其他带热源的部组件。随机振动环境和热学环境因素是航天产品设计开发过程中必须考虑的重要因素。在设计初期采用仿真方法开展结构强度分析验证，找到产品结构的薄弱环节，有利于结构的改进和优化，缩短产品研发周期和降低生产成本。[3-4]

1 有限元模型構建与验证

1.1 模型验证流程

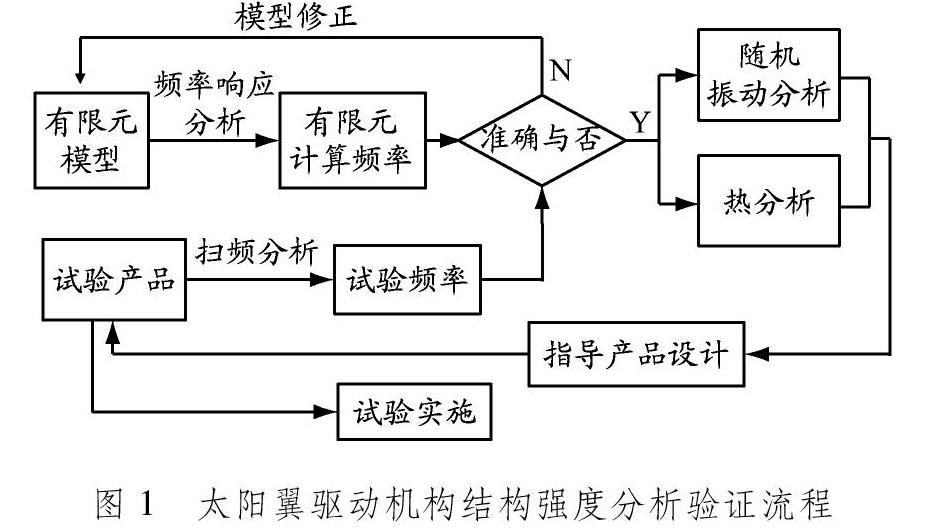
太阳翼驱动机构为典型空间机电结构，存在多处螺栓连接，各个零部件使用特殊的航天材料，这些结构特征导致分析模型的结构阻尼和材料阻尼具有不确定性，在设计阶段难以提供准确的模态阻尼参数。[5-7]因此，可以用模态阻尼参数验证有限元模型的准确性。太阳翼驱动机构结构强度分析验证流程见图1。在验证模型正确的基础上，开展随机振动分析和热分析。仿真结果可以验证结构强度设计的合理性，同时可以指导测试的实施。

1.2 有限元模型

1.2.1 模型离散

太阳翼驱动机构由主轴、前轴承组件（轴承和前轴承座）、后轴承组件（轴承和后轴承座）、电机组件（电机定子和电机转子）、旋变组件（旋转定子和旋转转子）、功率导电环组件（盘环体和上刷架盘）、信号导电环和结构件（主壳体、后壳体、下刷架盘和后盖）等组成。太阳翼驱动机构的零部件结构特征复杂，在HyperWorks中选取六面体单元将其离散为一系列单元，各单元在节点处相关联。相邻单元之间通过TIE连接方式模拟零部件之间的螺栓连接，传递力和力矩。太阳翼驱动机构有2个连接法兰：一个在产品的壳体上，与星体上的支架连接;另一个在太阳翼驱动机构输出轴端面上，与太阳翼根部铰链连接。太阳翼驱动机构会带动太阳翼一同转动，因此对太阳翼驱动机构主壳体的12个螺栓孔进行全约束，添加材料特性参数，得到太阳翼驱动机构的有限元模型，见图2。

1.2.2 模型修正

对太阳翼驱动机构进行特征级正弦扫频试验。以y方向为例，设定加速度为0.500g（g取9.8 m/s2），频率范围为10～2 000 Hz，得到太阳翼驱动机构结构y方向的基频为318.6 Hz，对应的加速度响应为14.962g，放大因子Q=14.926g/0.500g=29.924。模态阻尼比与动态放大因子互为倒数，因此得到系统的模态阻尼比为0.033。

有限元模型需要根据试验数据进行修正。对有限元模型进行y方向的正弦振动仿真分析，设定加速度为0.500g，频率范围为10～2 000 Hz，模态阻尼比为0.033，仿真计算得到太阳翼驱动机构结构y方向的基频为310.0 Hz，加速度响应为14.592g。计算频率响应点的误差为2.70%，响应值的误差为2.47%，都小于5.00%，在工程误差允许范围之内，验证构建的有限元模型合理有效，可以开展后续的仿真计算。[8]

2 数字化仿真

2.1 随机振动仿真分析

在太阳翼驱动机构结构设计过程中进行随机振动仿真分析，能有效预测结构关键部位在力学环境下的响应，为机构顺利通过力学环境试验提供参考。[9-12]太阳翼驱动机构随机振动激励载荷由力学环境试验条件确定。随机振动仿真分析条件见图3。

太阳翼驱动机构整体结构关于xOy平面对称，所以可以只研究结构在x和y方向上的响应。太阳翼驱动机构随机振动仿真分析结果见表1，应力云图和加速度响应曲线分别见图4～7。

由以上分析可以看出：结构最大应力出现在x方向，最大应力为59.43 MPa，小于材料的许用应力400 MPa，若取安全因数为6.73，则不会在峰值应力下发生破坏，满足结构强度要求。x方向为结构加速度响应最大值的方向，加速度均方根为796.94 m/s2，加速度均方根放大倍率为6.35，小于10，在安全裕度范围内，说明结构具有足够高的刚度和强度，安全性好，在力学环境下结构设计合理。

2.2 热学仿真分析

热学仿真分析主要针对太阳翼驱动机构产品在热循环和热真空条件下的温度分布情况进行分析。根据产品的鉴定级试验条件，确定热循环和热真空下的温度场曲线，分别见图8和9。

热循环下的热分布和热应力云图分别见图10和11。

由此可知：在施加热循环条件下，太阳翼驱动机构的最高温度出现在盘环体上，最高温度为245.6 ℃，最低温度为148.5 ℃;高温下的最大热应力出现在旋变组件位置，大小为402.6 MPa，低温下的最大热应力出现在轴承座上，大小为372.5 MPa，均小于材料的许用应力，说明在热循环下结构设计合理。

热真空下的热分布和热应力云图分别见图12和13。

在热真空条件下，太阳翼驱动机构的最高温度和最大热应力均出现在盘环体上：在70 ℃温度场，机构的最高温度为268 ℃，最大热应力为363.0 MPa;在-35 ℃温度场，机构的最高温度为183 ℃，最大热应力为262.1 MPa。热真空条件下的最大热应力均小于材料的许用应力，说明结构设计合理。

3 结束语

提出一种结构强度分析验证方法，建立太阳翼驱动机构的有限元模型，并通过试验验证其有效性。利用HyperWorks和Abaqus计算太阳翼驱动机构在随机振动环境和热环境下的结构强度，结果认为盘环体为强度薄弱环节，太阳翼驱动机构结构设计合理。该方法在产品设计前期节约时间和成本，为类似产品设计提供参考。建模精度在很大程度上取决于计算机性能和设计师的专业水平，有关模型更精确的验证还需要更多的试验数据支撑。

参考文献：

[1] 杨宝宁. 随机振动条件下设计载荷的确定方法[J]. 航天器工程， 2006， 15（3）：33-37.

[2] 舒盛荣. 应用有限元法的小型控制力矩陀螺结构可靠性分析[D]. 哈尔滨：哈尔滨工业大学， 2009：17-30.

[3] 董得义， 辛宏伟， 杨利伟， 等. 大孔径反射镜组件随机振动响应分析与试验[J]. 振动与冲击， 2011， 30（11）：74-78.

[4] 马兴瑞， 于登云， 孙京， 等. 空間飞行器展开与驱动机构研究进展[J]. 宇航学报， 2006， 27（6）：1124-1126. DOI：10.3321/j.issn.1000-1328.2006.06.001.

[5] 朱兴高， 卿寿松， 陈凤熹， 等. 随机振动环境下太阳翼驱动机构强度安全性设计分析研究[J]. 航天制造技术， 2017（3）：1-3. DOI：10.3969/j.issn.1674-5108.2017.03.001.

[6] 朱兴高， 陈凤熹， 张宁， 等. 基于HyperWorks的太阳翼驱动机构谐响应仿真分析[J]. 煤矿机械， 2017， 38（3）：56-58. DOI：10.13436/j.mkjx.201703022.

[7] OANA C， BENOIT R B. New three-dimensional plastic potentials for porous solids with a VON Mises matrix[J]. Comptes Rendus Mecanique， 2015， 343（2）：77-94. DOI：10.1016/j.crme.2014.12.001.

[8] VASSILIOU M F， MACKIE K R， STOJADINOVIC B. A finite element model for seismic response analysis of deformable rocking frames[J]. Earthquake Engineering & Structural Dynamic， 2017， 46（3）：447-466. DOI：10.1002/eqe.2799.

[9] LAN C B， QIN W Y. Enhancing ability of harvesting energy from random vibration by decreasing potential barrier of bitable harvester[J]. Mechanical Systems & Signal Processing， 2017， 85：71-81. DOI：10.1016/j.ymssp.2016.07.047.

[10] FANG K， WANG Z W. Statistical characteristics of maxima of contact force in stacked packaging units under random vibration[J]. Packaging Technology & Science， 2018， 31（5）：261-276. DOI：10.1002/pts.2313.

[11] ZHU X G， REN L M， CHEN F X. Safety verification of solar array drive assembly strength design based on mission profile[C]// Proceedings of 9th Conference of International Association for Advancement of Space Safety. Toulouse：IAASS， 2017.

[12] WIJKER J J. Random vibrations in spacecraft structures design：Theory and applications[M]. Heidelberg：Springer-Verlag， 2009：162-163.

（编辑 武晓英）