应用地理探测器改进地面沉降危险性评估模型的研究
2019-07-08石鹏远王彦兵
石鹏远,余 洁,朱 琳,王彦兵
(1.首都师范大学城市环境过程与数字模拟国家重点实验室培育基地,北京 100048;2.首都师范大学资源环境与旅游学院, 北京 100048;3.首都师范大学三维信息获取与应用教育部重点实验室,北京 100048)
0 引言
地面沉降作为一种在自然因素和人为因素下形成的地表垂直下降现象[1],能够对城市基础设施和建筑物(如农田、住宅、道路和输电线路等)造成破坏,使政府的财政和社会成本增加[2-3]。进行地面沉降危险性评估可以为城市规划、防灾减灾以及地质环境的恢复治理提供基础资料和科学依据,以避免或减轻地面沉降造成的损失[4]。
对地面沉降危险性进行评估的模型有多种。一些学者[5-8]采用土水模型法,从水位模型和土体力学模型着手,对地面沉降危险性进行评估,土水模型法的优点是能够基于精确的水文、土壤数据和地面沉降成因机理模拟预测地面沉降,但该方法需要大量的实地勘测数据以使土水模型的模拟条件与实际的水文、土壤状态吻合。另一些学者采用加权综合评价法[9-12],综合考虑各因子对地面沉降的影响程度,把各指标的优劣综合起来,用一个无量纲的评估分值加以集中,以表示地面沉降危险性,其中部分学者[13-16]采用因子叠加模型将与地面沉降相关的因子进行指标打分并进行多个栅格数据层的数学运算,按照人工赋予的叠加函数计算得到评估结果;另一部分学者[17-21]采用模糊层次分析模型,建立模糊评价矩阵为各项评估指标赋予不同的权重,计算各指标的评分加权总和并进行评估。加权综合评价法的优点在于灵活性和综合性强,能够根据评价目标有目的地调整参与评估的因子组,适合于对技术、决策或方案进行综合分析评价和优选,是一种较为常用的方法[22-24],然而在因子选取和指标权重确定的过程中,人为因素的判断会影响评估结果。在一些研究中,指标的权重由特尔斐法或学者直接确定[25-27];而采用模糊层次分析模型计算权重时,因子之间的重要性比较也常依靠特尔斐法或学者的专业判断[28-29]。这使因子的指标项权重的确定受到较强的人工干预,具有不确定性,进而影响评估模型的准确性。
为了减少指标权重确定过程中人工干预导致的不确定性,本文将地理探测器方法应用于加权综合评价法构建的地面沉降危险性评估模型中,以因子叠加模型和模糊层次分析模型为例进行改进。改进后的模型将根据各评估因子在地理位置上的分布与地面沉降分布的关联程度,从统计学的角度出发,定量地确定各项评估指标的权重,以期提高评估模型的准确性。
1 地面沉降危险性评估模型及因子指标
1.1 评估模型
本文共选取三种较常被使用的、便于操作的评估模型,考虑到因子叠加模型有多种运算函数,选择了较为常见的最大值因子叠加模型和加权因子叠加模型。第三种模型是模糊层次分析模型。对三种模型分别应用地理探测器进行评估指标权重确定环节的改进。
(1)最大值因子叠加模型
最大值因子叠加模型(Maximum Value Factor Overlapping, MVFO)在进行地面沉降危险性评估时,仅使用沉降特征因子指标(如沉降速率,累计沉降量)。对沉降特征因子进行危险性指标打分,并按栅格进行叠加运算,栅格中危险性分值最高的因子指标分值视为最终的沉降危险性估值。这一模型的优势在于参与评估因子的数量少,因子数据易于收集,评估过程简单快捷,基于沉降特征的评估较为符合地区近期的沉降状态,对高危险性估值的地区漏检率低;不足之处在于该模型不考虑推动沉降发展的诱发因子,缺少对沉降未来的发展趋势的估计,且对于沉降危险性较低的地区容易产生误判。危险性评估值计算公式为:
H危险性=max{N1,N2,…,Nn}(1)
式中:H危险性——沉降危险性最终估值;
Nn——第n项因子的指标评分;
n——因子总数。
(2)加权因子叠加模型
加权因子叠加模型(Weighted Factor Overlapping, WFO)在评估中既考虑沉降特征因子对沉降状态的表达刻画,又考虑沉降诱发因子对沉降发展趋势的预示作用。由于不同的地区沉降诱发因子不同,且诱发因子打分的指标也不同,因此该模型不取指标评分最大值为沉降危险性的最终估值,而是将每一个指标都视为具有单独的权重,在简化计算的前提下,各指标被认为权重相等。各因子进行指标打分并单独成图,按照栅格进行叠加运算,栅格的危险性最终估值为所有指标的平均分值。该评估模型的优势在于即包含能反映沉降状态的沉降特征因子又包含能揭示沉降未来趋势的沉降诱发因子,且操作简单便捷;不足之处在于模型忽视了不同因子与沉降关联的差异性,在评估中将各因子视为同等重要,对评估精度产生影响。危险性评估值计算公式为:
(2)
式中:H危险性——沉降危险性最终估值;
Ni——第i项因子的指标评分;
n——因子总数。
(3)模糊层次分析模型
模糊层次分析模型(Fuzzy Analytic Hierarchy Process, FAHP)是根据模糊数学方法与层次分析法建立的评估模型。考虑到不同因子与地面沉降的关联性具有差异,该模型通过不同因子之间的两两比较构建各因子对评估对象的隶属度函数,量化确定评估中各因子的指标分值所占权重。FAHP模型既解决了判断矩阵的一致性问题,也解决了解的收敛速度和精度问题,最终求得与实际相符的指标权重排序向量[18]。该模型的优势在于半定量地体现了不同因子作用的差异性,使评估结果更加合理有效;不足之处在于,在确定指标权重的过程中,对各因子进行的人工比较存在着不确定性,对评估精度产生影响。
该方法的模型建立过程如下[30]:
a.通过对因子的两两比较,建立优先关系矩阵F。矩阵标度取值范围为0.1~0.9。
(3)
式中:fij——矩阵F中因子i与因子j重要性判断标度;
s(i)——因子i的重要程度;
s(j)——因子j的重要程度。
fij值越高,说明因子i在与因子j的对比中显得更为重要。fij为0.5时,两个比较的因子同等重要。矩阵F是一个模糊互补矩阵,即fij=1-fji。
b.计算模糊一致性判断矩阵R。

c.通过和行归一法计算排序向量W0。
W0=(w1,w2,…,wn)T=

式中:W0——计算得到的排序向量;
wn——向量W0在第n行的值;
n——因子总数;
rij——矩阵R在i行j列的值。
e.以排序向量W0作为迭代初值V0,进一步求解精度较高的排序向量Vk。
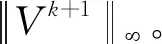
(5)
式中:Vk+1,n——特征向量Vk+1的第n行值。所得向量Wk=Vk+1,即为排序向量,迭代结束。
f.结合加权综合评价法模型计算最终的评估结果:
(6)
式中:H——最终评估指数;
Wi——计算出的第i项指标权重;
Ni——第i项因子的指标评分;
n——因子总数。
1.2 地理探测器对模型的改进
1.2.1地理探测器
地理探测器(Geographical Detector, GD)是由王劲峰等[31]所开发的一种新的统计学方法,该方法能够探测某一地理属性的空间分异性,并揭示其背后的驱动因子,例如探测某一地理属性Y和其解释因子X之间的关系。其核心思想基于的假设是:若某个因变量受到某一自变量的重要影响,那么因变量和自变量的空间分布应该具有相似性[32]。该方法的优势在于没有过多的假设条件与约束,能有效地克服传统统计分析方法处理类别变量时的局限性[33]。
地理探测器由四个探测器组成:因子探测器、交互作用探测器、风险区探测器、生态探测器,分别用于探测因子X对地理属性Y分布的影响程度、两个不同的因子X1和X2共同作用下对Y分布的影响、因子X的两个子区域属性值均值差异是否显著、X1和X2对Y的空间分布影响的差异是否显著。
本文使用因子探测器参与评估模型中因子指标的权重确定。因子探测器计算结果在本文中称为“因子驱动力”,其得到的计算结果用q值度量,q值越高,说明自变量X对因变量Y的影响越强;反之,则说明自变量X对因变量Y的影响较弱。q值的计算公式为:
(7)
式中:h=1,2,…,L——因变量Y或自变量X内部的分类或分区;
Nh和N——分别为层h和全区的单元数;
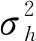
SSW和SST——分别为层内方差和与全区总方差;
q——值域为[0,1]。
1.2.2模型的改进
(1)地理探测器——最大值因子叠加模型
地理探测器——最大值因子叠加模型(Geographical Detector-Maximum Value Factor Overlapping, GD-MVFO)对MVFO模型沉降特征因子的指标分值比较过程进行了修改。根据地理探测器探测得到的各因子q值计算得到因子的指标权重。在选取危险性最高的指标时,各因子的比较分值等于因子的指标分值与指标权重的乘积。比较分值最高的因子,其指标分值将作为沉降危险性最终估值。
与MVFO模型相比,改进后的GD-MVFO模型在评估中不仅考虑沉降特征因子的指标分值大小,还考虑不同因子的影响差异,而不是将各因子视为同等重要。GD-MVFO模型危险性评估值计算公式为:
(8)
Cm=max{N1w1,N2w2,…,Nnwn}(9)
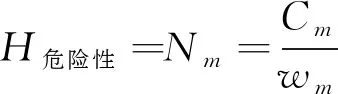
式中:wi——第i项因子的指标权重;
qi——第i项因子的因子驱动力;
n——因子总数;
Nn——第n项因子的指标分值;
Cm——因子m的比较分值;
wm——因子m的指标权重;
H危险性——沉降危险性最终估值。
(2)地理探测器——加权因子叠加模型
地理探测器——加权因子叠加模型(Geographical Detector-Weighted Factor Overlapping, GD-WFO)使用探测到的q值计算得到各因子的指标权重。与WFO模型相比,改进后的GD-WFO模型不仅综合了各因子的指标打分值,还考虑了不同因子的影响能力差异,不再将各因子视为同等重要。沉降危险性最终估值等于各因子对应的指标分值与指标权重的乘积之和。GD-WFO模型的公式如下:
(11)
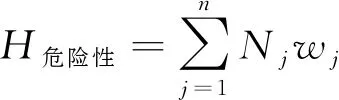
式中:wi——第i项因子的指标权重;
qi——第i项因子的因子驱动力;
n——因子总数;
Nj——因子j的指标分值;
wj——因子j的指标权重;
H危险性——沉降危险性最终估值。
(3)地理探测器——模糊层次分析模型
地理探测器——模糊层次分析模型(Geographical Detector-Fuzzy Analytic Hierarchy Process,GD-FAHP)在原有的FAHP模型的基础上,对生成因子优先关系矩阵的环节进行改进。根据对因子驱动力的探测结果而不是对因子的人工对比估值计算产生优先关系矩阵F。
GD-FAHP模型的建立过程如下:
a.首先根据探测出的q值计算生成因子驱动力比较矩阵Q,公式如下:
(13)
式中:Qij——因子i与因子j的因子驱动力比较值;
q——因子驱动力。
b.根据因子力比较矩阵Q计算生成优先关系矩阵F:
(14)
式中:Fij——因子i与因子j重要性判断标度;
Qij——因子i与因子j的因子驱动力比较值;
Qji——因子j与因子i的因子驱动力比较值。
c.将矩阵F带入模糊层次模型中,求得权重向量Wk。
1.3 因子指标
1.3.1评估因子选取
根据北京市地面沉降发生机理[34-35],综合考虑地面沉降灾害对社会经济可持续发展带来的严重影响,依照少而精、实用易操作、数据易获取等原则,参照地质灾害评估的行业规范、沉降因素研究文献和以往的地面沉降危险性评估文献,本文在进行地面沉降危险性评估时将地面沉降特征因子、地面沉降诱发因子作为评估因子。
(1)沉降特征因子
参照中华人民共和国国土资源部发布的《地质灾害危险性评估规范》[36]对地面沉降调查的内容规定及地面沉降发育程度分级表,本文选择地面沉降速率和地面累计沉降量两个因子作为沉降特征因子参与地面沉降危险性评估。
本文的地面沉降速率,采用基于永久散射体合成孔径雷达干涉测量技术和TerraSAR-X的微波遥感影像计算得到研究区2010年年均地面沉降速率。地面累计沉降量的选取,则根据其它文献中[37]已发布的北京市历史累计沉降量数据,采用1955~2010年的沉降值。沉降速率及累计沉降量分布见图1(a)和(b)。
(2)沉降诱发因子
有学者[38]的研究显示,北京市地下水开采对地面沉降影响最大,沉降中心与地下水位降落漏斗区高度吻合,是地面沉降的主要贡献因素。
北京地区的地面沉降分层沉降量被认为与对应层位上的黏性土占比呈正比例关系,其空间分布特征及变化趋势与平原区的地层结构及可压缩黏性土层厚度具有很好的一致性,整体由北西向的单一结构区向南东方向的多层结构区扩张。沉降速率大于50 mm/a的沉降区大多分布在黏性土层厚度大于100 m的地区,几大沉降中心与黏性土层厚度较大地区吻合较好。
还有学者[39]认为降水会通过对地下水补给和土壤含水量的变化间接影响到地面沉降发育状态。
根据以上原因,本文选取地下水水位变化速率、地下水水位标高、可压缩层厚度和年均降水量四个因子作为沉降诱发因子参与评估,见图1(c)~(f)。
1.3.2指标评分准则
目前在地面沉降危险性评估工作中,不同地区对各因子的指标评分标准存在差异。本文参照国家发布的地质灾害危险性评估规范文件[36]、危险性评估指导专著[1]及北京地区地面沉降危险性评估文献[4,15,18,21],结合研究区各因子的分布情况,制定指标评分准则(表1)。根据准则对各评估因子赋予危险性指标分值,并参与后续计算。
2 实验及验证
2.1 实验区概况
实验区位于北京市平原地区,地处东经116度20分至116度40分,北纬39度45分至40度5分之间(图2)。实验区面积约为385.51 km2,覆盖北京市东城区大部、朝阳区南部,并与西城区、丰台区、大兴区和通州区有少许交叠。实验区西侧的西城区和东城区地面沉降发育程度较低,西单到东单地区被认为是北京市最早发现沉降的地区[37](20世纪30年代中期)。东侧涵盖了朝阳来广营—金盏和东八里庄—通州城区—黑庄户两个沉降带的一部分,其中东郊八里庄大郊亭和来广营两个地区的沉降产生于20世纪70年代初到80年代初期工业发展需求导致的对地下水的大量开采;通州沉降区形成于80年代初至20世纪末,并在21世纪初迈入快速发展阶段[40]。到目前为止,实验区东侧部分地区平均年沉降速率超过50 mm/year,局部地区沉降速率超过100 mm/year。

表1 指标评分表
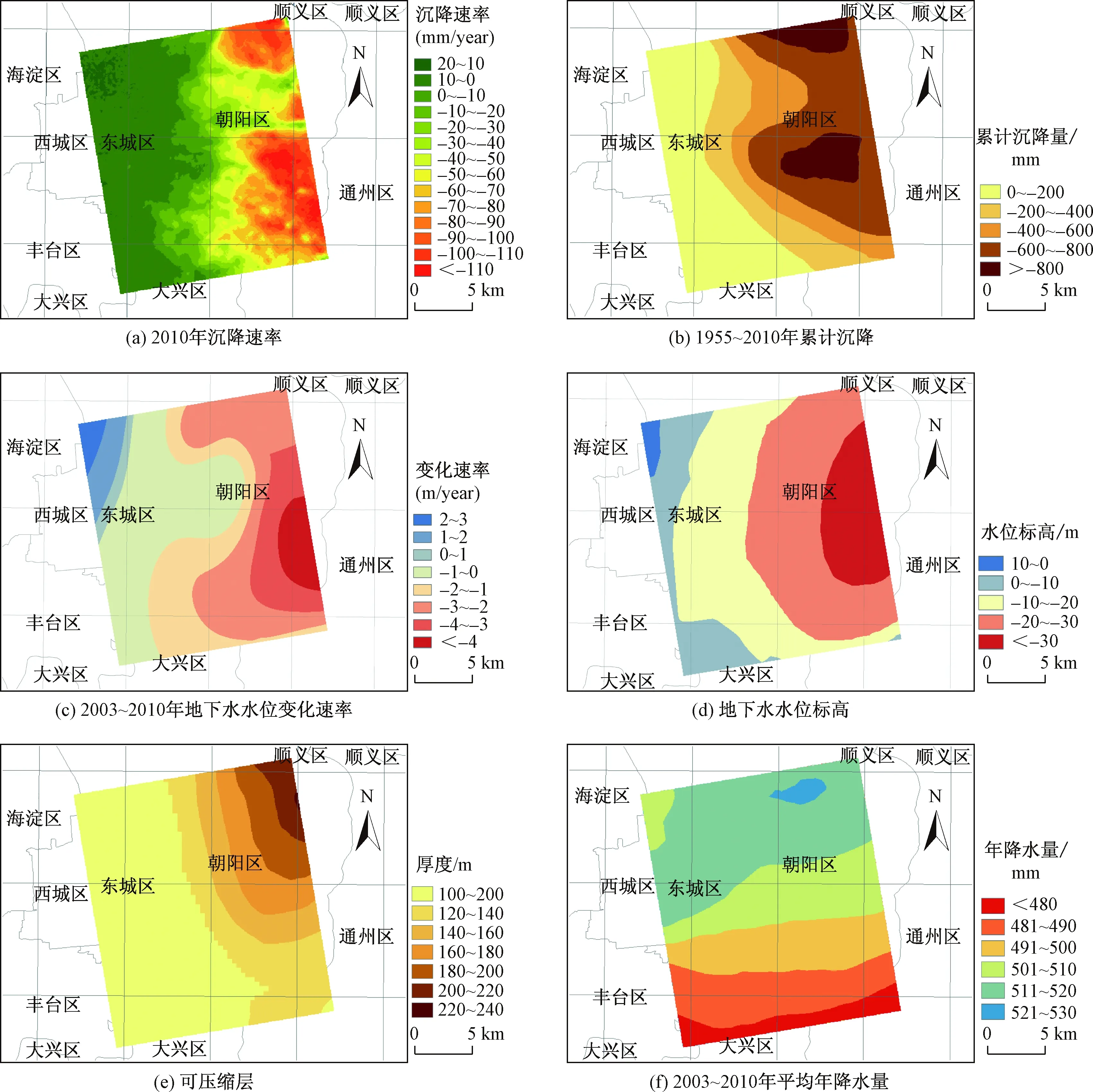
图1 因子分布图Fig.1 Distribution of factors
2.2 评估实验
2.2.1因子驱动力探测
在研究区中以500 m为间距生成1 545个采样点(图3),提取各因子位于采样点的值。评估实验的假设条件是基于2010年以前的因子分布数据对研究区2010年至2015年沉降发展做出估计。从评估者的角度出发,2010年以前的因子分布数据为已知量,可以作为自变量参与探测计算;2010至2015年的沉降量为未知量,不能作为因变量进行探测。根据沉降速率在时间上的连续性,将2010年沉降速率作为替代的因变量Y,所有因子作为自变量X进行因子驱动力(q值)计算(表2)。表中的p值为显著性检验值。
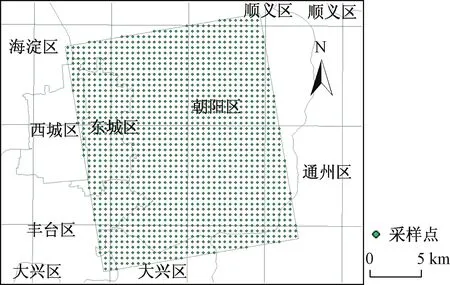
图3 采样点分布Fig.3 Distribution of sampling points
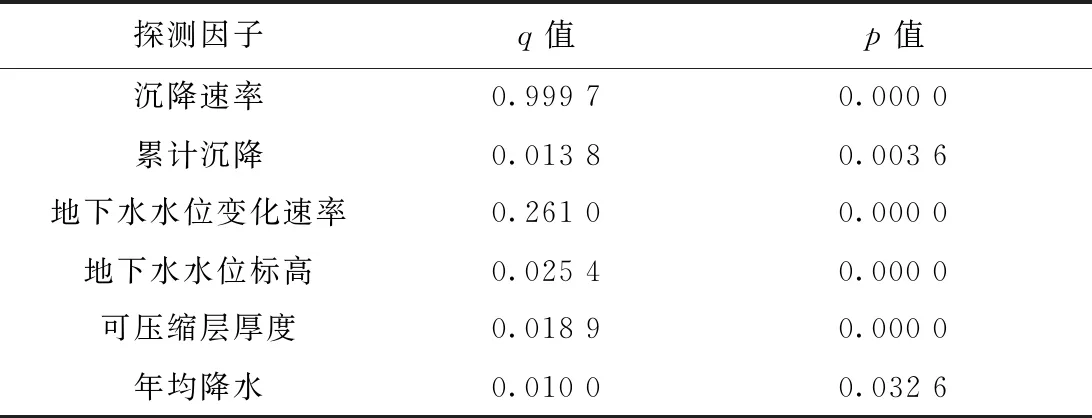
探测因子q值p值沉降速率0.999 70.000 0累计沉降0.013 80.003 6地下水水位变化速率0.261 00.000 0地下水水位标高0.025 40.000 0可压缩层厚度0.018 90.000 0年均降水0.010 00.032 6
2.2.2实验结果
(1)未改进的评估模型
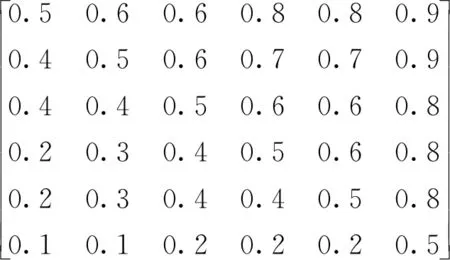
根据模型公式和指标评分表,MVFO、WFO、FAHP模型的评估结果见图4地面沉降危险性评估结果(a)~(c)。其中,FAHP模型的计算矩阵和最终权重如下所示:
a.优先关系矩阵F:
b.模糊一致性矩阵R:
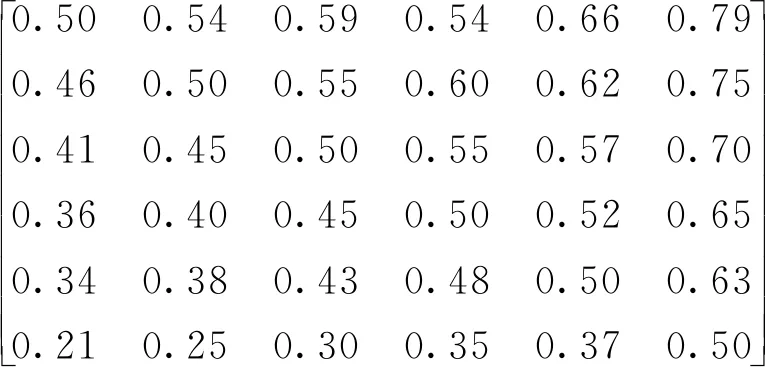
c.排序向量W0:
d.互反型判断矩阵E:
e. 权重向量Wk:
(2)改进后的模型
根据模型公式和指标评分表,GD-MVFO、GD-WFO、GD-FAHP模型的评估结果见图4地面沉降危险性评估结果(d)~(e)。
GD-MVFO模型中评估因子的指标权重为:
[0.986 4 0.013 6]T
GD-WFO模型中评估因子的指标权重为:
GD-FAHP模型计算矩阵和最终权重如下所示:
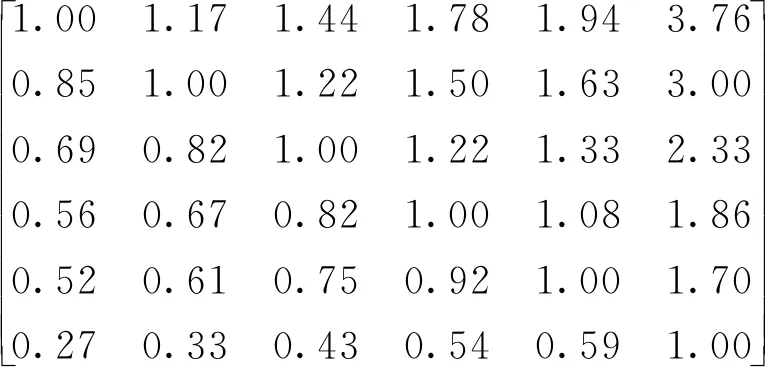
a.因子驱动力比较矩阵Q:

b.优先关系矩阵F:

c.将矩阵F带入模糊层次模型后,求得最终权重向量Wk:
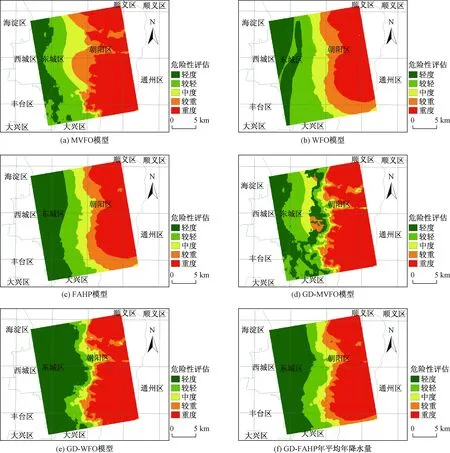
图4 地面沉降危险性评估结果Fig.4 Assessment results of land subsidence hazard
2.3 结果验证
2.3.1InSAR监测的沉降危险性

图5 InSAR监测沉降速率及沉降危险性分布Fig.5 Actual subsidence rate and subsidence hazard distribution
根据InSAR监测的2010年至2015年沉降值计算得到年均沉降(图5(a)),并参照危险性的指标评分表中对沉降速率的危险性评语,得到作为验证标准的沉降危险性分布(图5(b)),该图将作为衡量各评估模型利用2010年因子数据对2011~2015年(相对于因子数据的未来五年)的沉降危险性进行评估的结果准确性参照标准。
以250 m为间距获取验证结果的采样,根据验证采样点提取模型评估结果和作为对照的沉降危险性。
2.3.2模型评估结果与目标评语的匹配系数
根据验证采样点提取到的评估数据计算得到模型评估结果与目标评语的匹配准确度,验证结果如表3所示,在未改进的模型中,MVFO模型从“轻度”到“重度”五项评语准确度及总体准确度分别为30.15%、40.37%、44.31%、78.67%、100%和60.51%;WFO模型为40.25%、40.91%、44.31%、50.95%、74.26%和53.73%;FAHP模型为63.36%、43.85%、50.00%、49.05%、75.81%和65.05%。在应用地理探测器改进的模型中,GD-MVFO模型从“轻度”到“重度”五项评估准确度及总体准确度分别为49.48%、93.32%、89.82%、83.89%、100.00%和75.23%;GD-WFO为91.67%、63.37%、68.56%、70.85%、97.88%和89.56%;GD-FAHP模型为72.95%、54.28%、69.46、53.79%、89.45%和76.38%。

表3 模型评估结果准确度
2.3.3Kappa系数
在通常情况下,总体准确度能很好地表示评估结果与目标评语的匹配准确度,但是当某一类目标评估的验证采样点占据多数时,总体准确度受到该类别评估的影响较大,可能出现评估模型的偶然性高准确度。为进一步验证各模型的评估效果,使用Kappa系数进行分析。Kappa系数计算结果通常在0到1之间,系数越大表示一致性越高。
计算结果表明,MVFO模型、WFO模型、FAHP模型的Kappa系数分别为0.485 1、0.405 2、0.525 5。GD-MVFO模型、GD-WFO模型、GD-FAHP模型的Kappa系数分别为0.663 7、0.842 9、0.665 1。
2.3.4F1-measure函数
匹配准确度从验证采样点目标真实评估值的角度出发验证模型评估效果,此外还可以从评估结果的角度出发验证评估模型的某一类危险性评语对目标真实评语值的估计能力。为兼顾两种验证角度,进一步验证各模型的评估效果,使用F1-measure函数进行计算,F1-measure值越高说明评估模型越有效。
计算结果表明,MVFO模型、WFO模型、FAHP模型的F1-measure平均值分别为55.58%、49.43%、53.82%。GD-MVFO模型、GD-WFO模型、GD-FAHP模型的Kappa系数分别为75.39%、76.27%、63.74%。
3 结论
本文应用地理探测器,分别对MVFO模型、WFO模型和FAHP模型进行了改进,将改进模型的地面沉降危险性评估与三种未改进的评估模型进行了结果验证和对比分析,得到如下结论:
(1)改进后的评估模型在评估因子的指标权重确定环节中使用地理探测器进行因子驱动力的探测,根据因子与未来发育的地面沉降在空间分布上的相似关系,定量地计算并确定各项因子指标的权重值,替代了人工打分在指标权重确定环节中的作用,减少了评估工作因人工干预作用的差异而产生不同结果的可能性。
(2)与三种未改进的评估模型相比,应用地理探测器方法改进的GD-MVFO模型、GD-WFO模型、GD-FAHP模型与用作验证的地面沉降分布拟合度更好,表明将地理探测器应用于地面沉降的危险性评估是一种可行的方法,提升了评估模型的性能。
