含水量对黄土边坡稳定性的影响
2019-07-08袁中夏赵未超叶帅华朱彦鹏
袁中夏,赵未超,叶帅华,沙 浩,朱彦鹏
(1.兰州理工大学土木工程学院, 甘肃 兰州 730050;2.兰州理工大学西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050)
0 引言
黄土滑坡是我国黄土地区的主要地质灾害类型,它发育广泛,具有多发性和群集性的特点,并对当地生命和财产安全造成巨大威胁。如1983年发生在甘肃东乡县的洒勒山滑坡造成了震惊全国的人员伤亡[1];而长10 km、高120 m左右的甘肃永靖黑方台地区,自20世纪60年代以来先后发生过140余次大小滑坡[2]。文献[1]和[2]及其他文献[3-5],均认为降雨和灌溉引起土体含水量增高使得土体强度降低是诱发黄土滑坡的重要原因。
本文利用兰州七里河区兰工坪附近黄土边坡,通过原状黄土增湿后强度试验,获得不同增湿条件下黄土抗剪强度的变化规律。然后分析了黄土边坡稳定性随含水量的变化规律,可作为判定黄土含水量变化对边坡的稳定性影响的依据。
1 黄土试样及试验方法
1.1 黄土的物理性质
试验土样取自兰州七里河区兰工坪附近黄土边坡。原状马兰黄土土样的基本物性指标见表1,它的粒度组成见表2,微结构电镜图像见图1。

表1 原状黄土的物理性质指标

表2 原状黄土的粒度组成
从图1可以看出,该原状黄土以粉粒为主,颗粒之间形成了较大的孔隙,黏粒相互吸附形成黏粒团或者附着在大颗粒周围,黄土结构的胶结性较弱。

图1 原状黄土的SEM微结构图像(×450)Fig.1 SEM microstructure of undisturbed loess
1.2 试样制备
为了研究含水量对原状黄土抗剪强度的影响,试样采用天然状态和增湿后的原状黄土试样进行研究。制备增湿试样时,通过向环刀中土样上缓慢滴水增湿,达到所需配置的含水量为止。然后将增湿后的原状试样用塑料膜包裹并密封闷置48 h,以使试样内部含水量分布均匀。研究配制的含水量分别为5%、9%、13%、18%、22%,每个含水量下配置至少4个平行试样,加上原状土样,准备六组至少24个试样。各组试样的物性指标参数见表3。

表3 各组黄土试样的物性指标参数
1.3 试验方案
本试验利用直剪仪进行固结快剪试验。在应变控制式直剪仪(四联仪)上对试样分别施加100 kPa、200 kPa、300 kPa、400 kPa的竖向压力,待固结稳定后快速施加水平剪力(剪切速率为0.8 mm/min),将试样在3~5 min内快速剪断。本次试验共6个试样组,每组试验记录的结果取其峰值抗剪强度;对于无明显峰值的,取应力应变硬化曲线上变形量为4 mm时对应的强度作为试验结果。
2 含水量变化对黄土抗剪强度的影响
通过直剪试验得到不同含水量下黄土的抗剪强度线(图2)。从图2可以看出,随着含水量的增加,同一竖向压力下,黄土的抗剪强度减小。就强度线而言,含水量增加时,黄土的强度线下移。
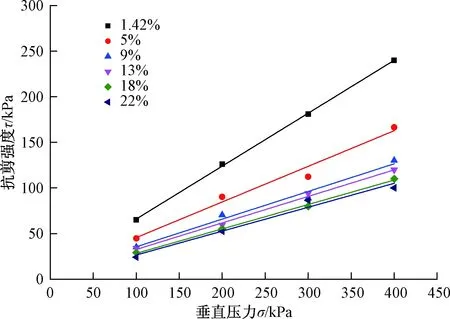
图2 不同含水量下黄土的抗剪强度线Fig.2 Shear strength lines of loess under different watercontent
表4是图2中不同含水量下抗剪强度线拟合得到的抗剪强度参数。
2.1 不同含水量下原状黄土的抗剪强度
将前面的试验结果,按照含水量的不同进行处理,可以得到不同竖向压力下抗剪强度随含水量的变化见图3。
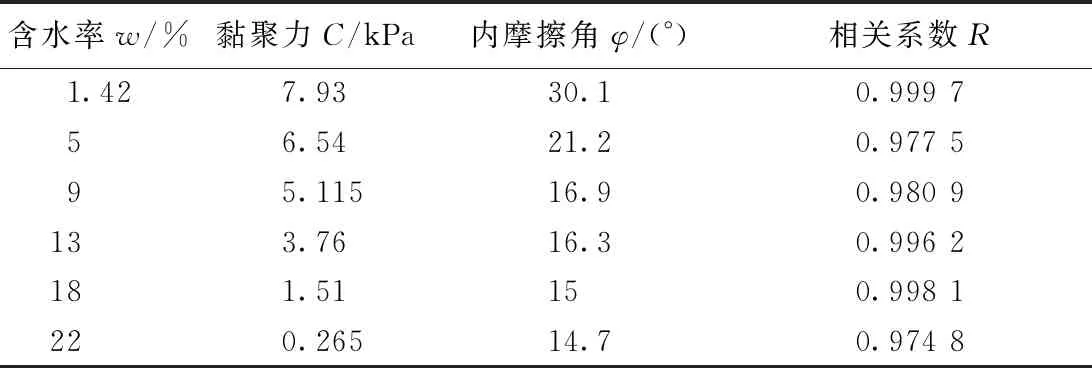
表4 不同含水量下黄土的抗剪强度参数

图3 原状黄土的抗剪强度随含水量的变化曲线Fig.3 Change of shear strength of the loesssamples with water content
从图3可以看出,相同含水量下,抗剪强度随竖向压力的增大而增大,这与土的抗剪强度公式一致; 在相同的竖向压力的作用下,抗剪强度的变化趋势是随着含水量的增大而减小。具体分析抗剪强度随含水量的变化,可以将其分为2个阶段: ①在含水量达到10%之前,抗剪强度随含水量的增加衰减很快; ②当含水量大于10%以后,抗剪强度随含水量的减小变缓。因此,存在某一界限含水量,当土体中含水量低于界限含水量时,原状黄土的抗剪强度受含水量影响显著;当含水量高于界限含水量时,原状黄土的抗剪强度随含水量变化减缓,这既反映了黄土的抗剪强度具有水敏感性的特征[6],也反映了基质吸力对黄土抗剪强度的贡献。袁中夏对兰州黄土土水特征曲线的研究表明在体积含水量高于15%,即质量含水量11%左右时,基质吸力迅速减小[7]。因此,当含水量高于10%时,黄土中基质吸力大大减小,其抗剪强度与低含水时相比也有较大的降低。
图3中原状黄土的抗剪强度随含水量的变化可以用公式(1)所表示的幂函数来描述。
τf=AwB(1)
式中:τf——抗剪强度;
w——含水量;
A、B——该函数的拟合参数。
表5给出了不同抗剪强度下公式(1)的拟合参数及拟合优度。表5表明,不同围压下公式(1)的拟合优度都大于0.9,因此,该幂函数可以较好地描述原状黄土增湿后抗剪强度随含水量的变化规律。
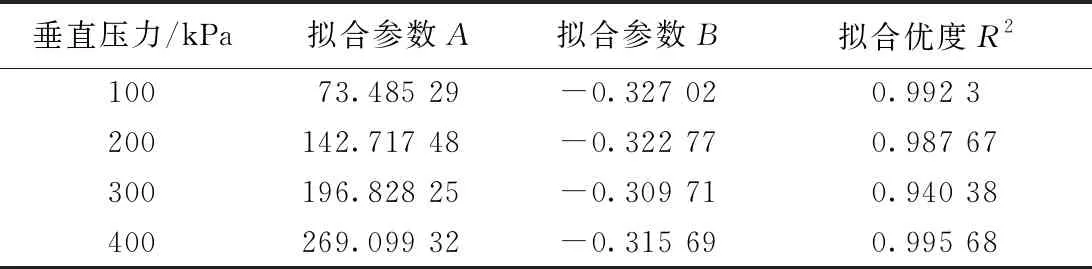
表5 黄土抗剪强度随含水量变化的幂函数拟合参数
2.2 黏聚力随含水量变化
为了进一步确定含水量对黄土抗剪强度影响的规律,对不同含水量下的抗剪强度指标——黏聚力和内摩擦角随含水量进行了分析。
图4是不同含水量下,黏聚力随含水量的变化。可以看出,黏聚力随含水量的增加大体线性减小,但是当含水量增加到18%以上时,随着含水量的进一步增加黏聚力变化很小。从微结构角度进行分析,当含水量增加时,使土颗粒间的结合水膜变厚,进而降低土颗粒间吸附作用,导致黏聚力降低[8]。但是黄土是一种弱黏性土,其黏聚力比较小,在本次试验中即便含水量很低时,也仅仅为8 kPa,因此,虽然黏聚力随着含水量的变化逐渐减小,但是除非上覆土压力很小,黏聚力对抗剪强度的影响相对较小。

图4 黄土的黏聚力随含水量变化Fig.4 Change of cohesion of loess with water content
2.3 内摩擦角随含水量变化
同样地,可以利用表4的数据,得到如图5所示的内摩擦角随含水量变化的关系曲线,由图5可以看到,随着含水量增大,内摩擦角逐渐减小,最后渐趋稳定至15°左右。

图5 黄土的内摩擦角随含水量的变化曲线Fig.5 The change ofinternal friction angle with water content of loess
为便于分析,可以将tanφ作为变量,考虑其随含水量的变化规律,这与直接分析内摩擦角的变化实际上是一致的。tanφ随含水量变化可以用幂函数拟合如公式(2):
tanφ=kwd(2)
式中:k、d——该函数的拟合参数。本试验数据得到的k为0.635 93,d为-0.309 66;拟合优度为0.979 58。
前面的数据表明黏聚力很小,随含水量变化总体不大,因此,当上覆土压力较大时,可以忽略黏聚力影响,不同湿度下黄土的抗剪强度可以将公式(2)代入到抗剪强度公式,并忽略黏聚力C得到简化的考虑含水量影响的抗剪强度公式:
τf=kσwd(3)
式中:σ——法向压力;
k,d——均为拟合参数。
实际上对(3)乘以一个系数δ(取值1.1~1.04),所得的抗剪强度就与试验数据相似,且这个系数是随着上覆土压力的增大而减小(随着上覆土压力增加,黏聚力在总强度中的贡献越来越小),随着含水量的增大而减小(高含水量时,黏聚力降低)。当压力较大或者含水量较高时,δ就无限接近于1。即在黄土高边坡和含水量高的黄土边坡,可以不考虑黏聚力的影响。(3)式可改成:
τf=δkσwd(4)
式中各参数含义同前文。
3 含水量对黄土边坡稳定性的影响
3.1 数值计算模型
黄土中含水量对其抗剪强度有显著影响,也必然影响到黄土边坡的稳定性。为了进一步研究含水量对黄土边坡稳定性的影响规律,利用Geostudio软件代入试验数据(含水量分别为天然状态、5%、9%、13%、18%和22%这六种情况下的强度指标),并采用两种典型的滑坡计算方法:比较实用的简化的Bishop法和理论上更为完善的Morgensten-Price法[9]进行滑坡稳定性计算。
计算的模型采用图6所示的均质黄土边坡。模型的底部固定,两侧土层受水平约束作用,计算不考虑地下水,除了考虑土的含水量变化引起的强度变化外,模型坡高(H)和坡比(1∶m)也分别变化。
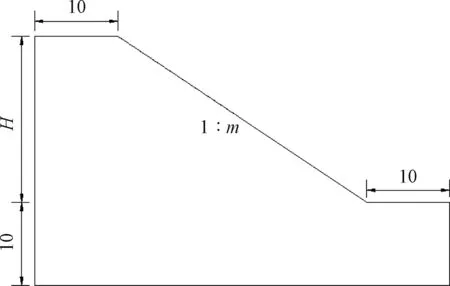
图6 黄土边坡数值计算模型Fig.6 Numerical model adopted for loess slope stability calculation
3.2 计算结果分析
改变图6模型中边坡的几何参数,得到4个均质黄土边坡模型。1号模型的坡高20 m、坡比1∶1.5,2号模型的坡高30 m、坡比1∶1.5,3号模型的坡高50 m、坡比1∶1.5,4号模型的坡高20 m、坡比1∶1。将不同含水量下黄土的强度参数代入计算,进行以上均质黄土边坡模型稳定性分析,其中1号和4号模型黄土边坡的最危险滑移面随不同含水量的变化分别见图7和图8。可以看出,随着含水量增加,最危险滑动面的位置向边坡坡面侧移。

图7 不同含水量下1号模型的最危险滑移面Fig.7 The least stable slide surface of model 1 under different water content
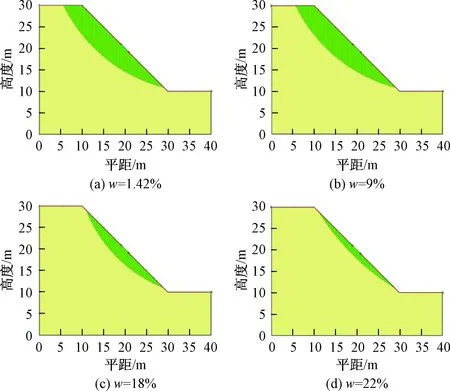
图8 不同含水量下4号模型的最危险滑移面Fig.8 The least stable slide surface position of model 4 under different water content
四个模型下,计算得到不同含水量时黄土边坡的稳定性系数见表6。
从表6中可以看出:不同情况下,利用两种方法计算所得边坡稳定系数基本一致;随着含水量的增加,黄土土坡的稳定性系数逐渐减小,以Bishop方法得到的稳定性系数考虑,1号模型最大减小到天然含水量下的33%,2号最大减小到天然含水量下的35%,3号模型最大减小到原来的38%,4号模型最大减小到原来的30%。据此可以总结出,相同坡比下,坡高越高,稳定性系数减小越多;相同高度下,坡比越大,稳定性系数减小越多。

表6 不同含水量下黄土边坡的稳定性系数
将表6中简化的Bishop方法计算所得稳定性系数与含水量作图,得到不同边坡模型下稳定性系数随含水量变化的曲线。
图9表明,随着含水量逐渐增大,黄土边坡的稳定性系数下降的速率由快变慢,且该稳定性系数随含水量变化规律也可以用公式(5)表示的幂函数来描述,不同边坡下拟合优度都超过0.95。
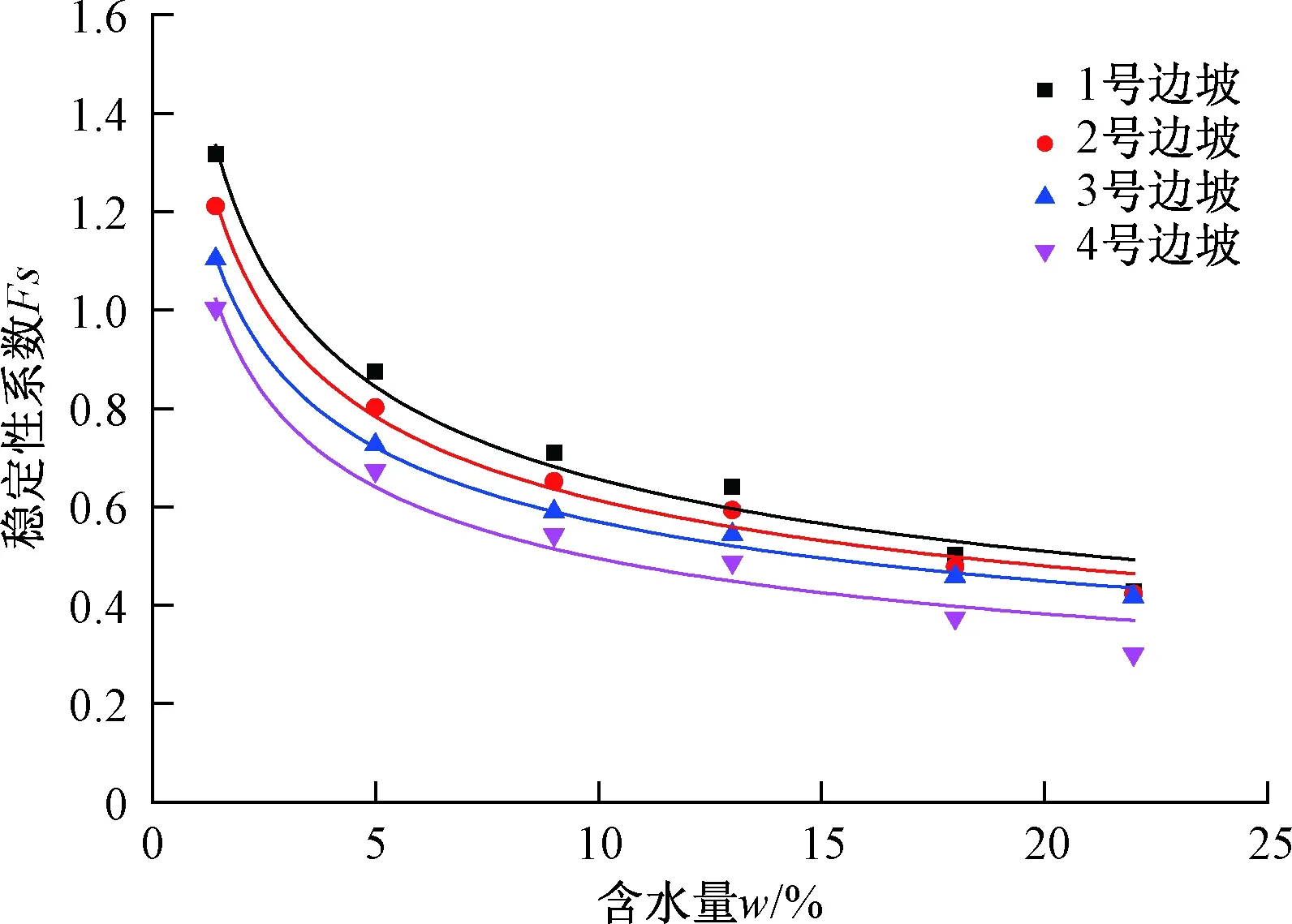
图9 Bishop法黄土边坡稳定性系数随含水量变化Fig.9 Factor of slope stability of loess slope under different water content calculated with Bishop method
式中:Fs——稳定性系数;
w——含水量;
Y、T——该幂函数的拟合参数。
进一步分析黄土边坡的稳定性系数与边坡高度的关系,得到如图9所示的结果。显然,同一含水量下,边坡稳定性系数随着边坡高度增加线性降低。
如果将边坡高度的影响也考虑进来,那么可以用公式(6)来表示含水量和坡高对边坡稳定性系数的影响:
Fs=Y×wT-m×H(6)
式中:m——拟合参数;
H——坡高。
利用表6的数据,得到拟合参数Y为1.533 81,T为-0.333 15,m为0.003 32,拟合优度为0.996。拟合参数Y远大于m,而坡高和以百分比表达的含水量相比,最大只有35倍,因此,拟合结果表明,相对于含水量,坡高对稳定性系数的影响要小很多。从图10也可以看出,当含水量达到9%以上时,一定含水量下,边坡稳定性系数随边坡高度的变化幅度很小。当含水量分别为9%、13%、18%和22%时,边坡稳定性系数因坡高不同而变化的幅度对应以上含水量值,分别仅为0.12,0.1,0.04和0.01。因此,当含水量不太低时,高度对边坡稳定性系数的影响基本可以忽略。

图10 Bishop法计算得到不同坡高黄土边坡稳定性系数变化Fig.10 Change of factor of slope stability of loess slope with different slope height calculated with Bishop method
利用坡高相同,坡比不同的1号和4模型比较不同坡比时不同含水量下黄土边坡的稳定系数变化,结果见图11。
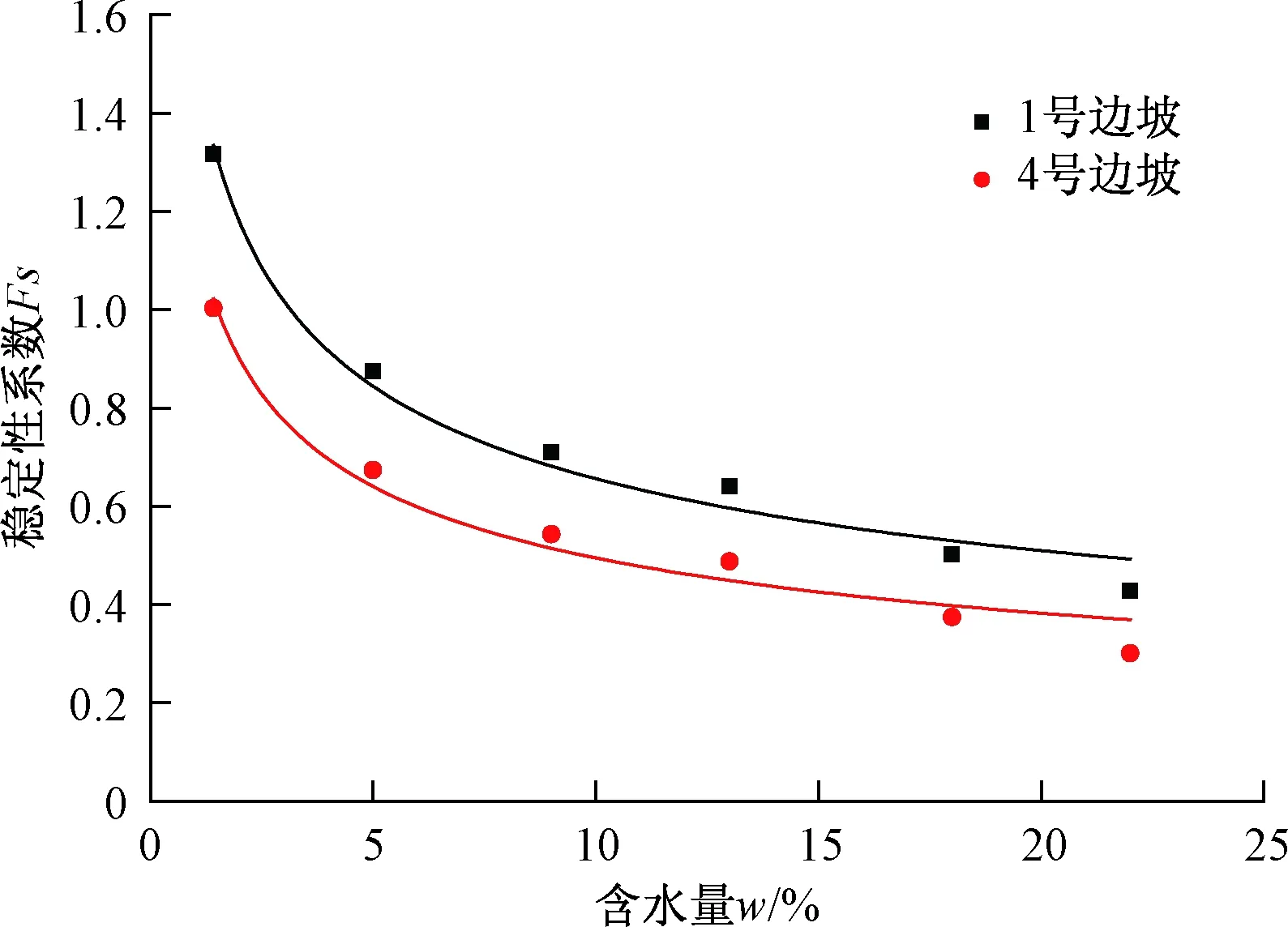
图11 不同坡比下含水量对黄土边坡稳定性系数的影响Fig.11 Influence of water content on of factor of slope stability of loess slope with different slope ratios
从图11可以看出,不同坡度下,均质黄土边坡的稳定性系数随含水量变化的趋势是一致的,都是低含水量下稳定性系数减小较快,而当含水量达到18%以上时,减小变得缓慢。
4 结论
本文基于室内原状黄土和增湿黄土的抗剪强度试验,分析了含水量对黄土抗剪强度的影响,并进一步利用抗剪强度数据进行了不同含水量下的边坡稳定性分析,得到含水量对黄土边坡稳定性的影响的规律,研究的主要结论如下:
(1)黄土抗剪强度随着含水量的增大而以幂函数形式减小,并且存在某一界限含水量,当土体中含水量低于界限含水量时,抗剪强度受含水量影响显著;当含水量高于界限含水量时,抗剪强度变化趋缓。
(2)黄土含水量较低时,抗剪强度指标黏聚力和内摩擦角均较高,而含水量增加时,二者均降低。但是由于黄土的黏聚力比较小,所以相对于内摩擦角,其变化对抗剪强度的影响较小,当上覆土层较厚时,黏聚力的变化可以忽略。
(3)随着含水量的增加,黄土边坡的稳定性系数逐渐降低且下降的速率由快变慢;稳定性系数随含水量变化规律也可以用幂函数来描述。当选取不同的坡度进行计算分析时,均质黄土边坡的稳定性系数随含水量的变化规律仍然一致。
(4)当坡度一定时,坡高对黄土边坡的稳定性系数也存在一定影响,但这个影响相对于含水量的影响较小。特别当含水量不太低时坡高的影响可以忽略。
(5)综合以上认识,可以认为含水量导致的黄土抗剪强度降低,对黄土边坡的安全性有很大影响。黄土边坡的治理中采取适当的排水和防渗措施往往十分必要。
(6)本研究中采用了简化的均质黄土边坡模型,有利于剔除其他因素的影响,得到含水量变化对黄土边坡稳定性影响的规律。该结果适用于未发生滑坡的原状黄土边坡。
