“三杆+轨”问题的试题编制与分析策略
2019-07-08福建
福建
“三杆+轨”问题是中学“杆+轨”模型在单杆和双杆题型基础上衍生的一种新的物理模型。作为中学物理考查动生类电磁感应问题的重要载体,三杆与导轨的结合不仅使试题延续了传统“杆+轨”问题中的研究对象多、综合知识点多、分析情境复杂、知识和能力综合性强等特点,而且还增强了对学生物理思维、科学探究等核心素养的考查。不论对教师命题还是学生解题都是一个新的研究课题,因此积极探索三杆问题的命题情境和分析策略,编制契合高考考纲要求的试题体系,对增强学生物理建模的能力,培育学生处理问题的能力,提升学生物理思维都具有积极的意义。
【方向1】三杆均置于磁场内,杆1切割,束缚杆2、3均处于静止。
【设计思路】设计三根导体杆放置于同一磁场或不同磁场内(如图1),其中杆1切割磁感线,而杆2和杆3均于磁场中处于静止状态。

图1
【分析策略】杆2和杆3在磁场中相当于电阻,模型的本质仍是单杆问题,解题时可分别对动杆和束缚杆进行受力分析,动杆按单杆模型动态分析,综合法拉第电磁感应定律、欧姆定律、牛顿运动定律、动能定理求解,受外力约束而静止的束缚杆应用平衡条件处理,然后以电流强度作为桥梁联立分析即可,在分析时要注意电源的位置及三杆的连接方式。
【例1】如图2所示,间距为L、电阻不计的平行金属导轨OPQ和LMN分别固定在两个竖直面内,在水平面PQMN区域内有方向竖直向上、大小为B1的匀强磁场,倾角为θ的斜面OPML区域内有方向垂直于斜面向上、大小为B2的匀强磁场。将质量为m、电阻为R、长为L的三根导体棒放置在导轨上,其中棒2的两端分别固定在P、M点,表面粗糙的棒3放置在倾斜导轨上,刚好不下滑,光滑的棒1在水平外力作用下由静止开始以恒定的加速度a沿水平导轨向右运动,棒1始终与导轨垂直且两端与导轨保持良好接触,滑动过程中始终处于竖直磁场中,重力加速度为g。求:
(1)棒3刚要向上滑动瞬间,棒3中电流I的大小和方向;
(2)棒3刚要向上滑动瞬间,水平外力的功率P。
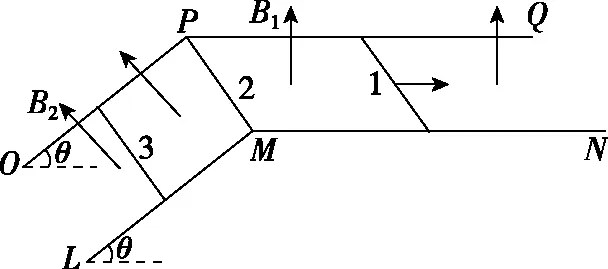
图2
【解析】(1)开始时,棒3刚好不下滑,根据平衡条件
mgsinθ=Ff
棒3刚要上滑的瞬间,根据平衡条件
B2IL=mgsinθ+Ff
通过棒3的电流方向沿棒垂直纸面向里。
(2)将棒2、棒3看成定值电阻,根据串并联关系得
I总=2I
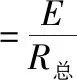
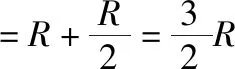
以棒1为研究对象,根据法拉第电磁感应定律得
E=B1Lv
根据牛顿第二定律F-B1I总L=ma
棒3刚要上滑的瞬间,拉力的功率P=Fv
【点评】棒2和棒3受约束处于静止状态,在电路中可看成定值电阻,棒1在磁场中做切割磁感线运动产生感应电动势,根据回路的串并联关系可得出棒1和棒3电流的关系,对棒3受力分析,由平衡条件可求出通过棒3的电流大小及方向,结合感应电动势、闭合电路欧姆定律、牛顿运动定律和功率公式即可联立求解。
【方向2】三杆均置于磁场内,杆1切割,杆2处于静止,杆3沿磁场方向共线运动(v3∥B)。
【设计思路】设计三根导体杆放置于同一磁场或不同磁场内(如图3),其中杆1运动切割磁感线,而杆2约束处于静止状态,杆3(共线杆)于磁场中沿磁场方向运动。
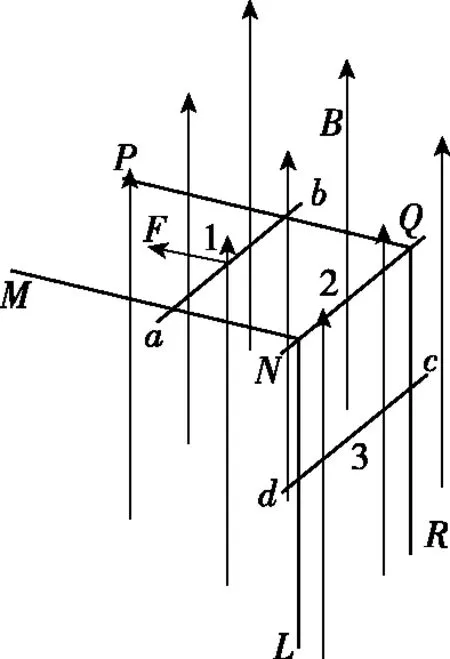
图3
【分析策略】杆2受约束处于静止状态,相当于定值电阻,共线杆由于速度方向平行于磁场方向没有产生感应电动势,模型的本质仍是单杆问题,题型分析策略是切割杆按单杆模型进行分析和处理,受外力束缚而静止的束缚杆根据平衡条件处理,共线杆则进行动态分析,寻找最终稳态的动力学关系,以电流为桥梁联立三杆方程进行求解。
【例2】相距L=1 m的足够长金属导轨竖直放置,质量为m1=1 kg的金属棒ab和质量为m2=0.27 kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上,金属棒ef固定于金属导轨上,如图4所示,虚线上方磁场方向垂直纸面向里,虚线下方磁场方向竖直向下,两处磁场磁感应强度大小相同。ab棒光滑,cd棒与导轨间动摩擦因数为μ=0.75,三棒的电阻均为R=0.3 Ω,导轨电阻不计。t=0时刻起,ab棒在方向竖直向上、大小按图5所示规律变化的外力F作用下,由静止沿导轨向上匀加速运动,同时由静止释放cd棒。(g取10 m/s2)
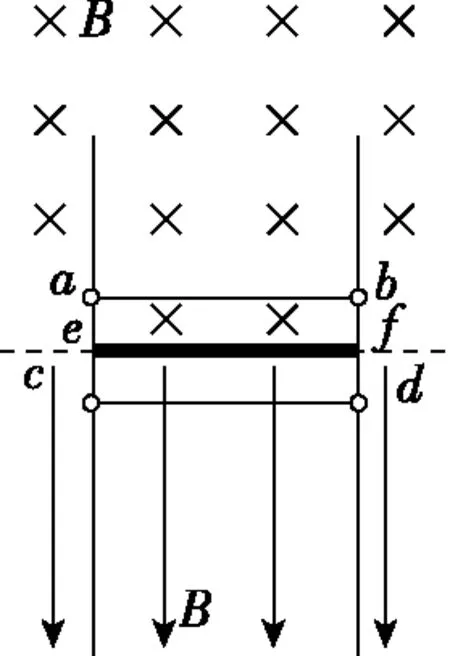
图4
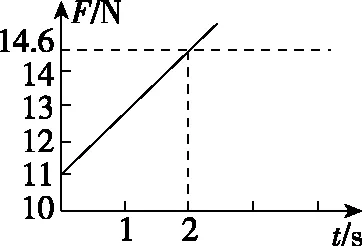
图5
(1)求磁感应强度B的大小和ab棒加速度大小;
(2)已知在2 s内外力F做功40 J,求这一过程中金属棒cd产生的焦耳热;
(3)求出cd棒达到最大速度所对应的时刻t1。
【解析】(1)导体棒ab在匀加速运动的过程中,ef棒始终处于静止,cd棒运动方向与磁场方向平行没有产生感应电动势,闭合回路仍为单电源问题。
设经过时间t,金属棒ab的速率v=at
回路中的感应电流为
对金属棒ab,由牛顿第二定律得
F-m1g-BIL=m1a
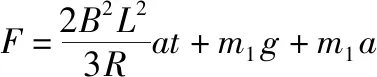
由图5可知
t1=0时,F1=11 N
t2=2 s时,F2=14.6 N
代入解得a=1 m/s2,B=0.9 T
(2)在2 s末金属棒ab的速率vt=at=2 m/s
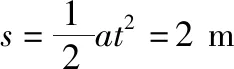
电路中产生的总热量Q=6Qcd
联立以上方程解得Qcd=3 J
(3)由题意可知,cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大;然后做加速度逐渐增大的减速运动,最后停止运动。
当cd棒速度达到最大时,有m2g=μBIcdL
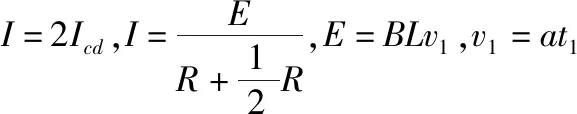
整理得t1=4 s
【点评】棒ef受约束处于静止状态,在电路中可看成定值电阻,棒ab运动产生感应电动势,棒cd共线杆没有感应电动势,本题仍为单电源问题,结合单杆问题的分析思路和数学知识(斜率和截距),即可求磁感应强度B的大小和ab棒加速度大小;动态分析cd棒的运动情况,得出当cd棒所受重力与滑动摩擦力相等时,速度达到最大,由平衡条件可求出电路中的电流,再由E=BLv、欧姆定律和运动学公式结合求解时间t1。
【方向3】两杆发生完全非弹性碰撞,碰撞后与杆3在磁场中同时切割磁感线。
【设计思路】设计三根导体杆放置于同一磁场、不同磁场或磁场内外(如图6),其中杆2运动与杆3发生完全非弹性碰撞,碰后三杆于磁场中切割磁感线。
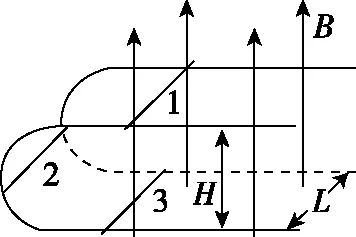
图6
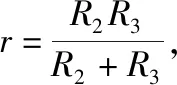
【例3】如图7所示,一上、下两层均与水平面平行的U形光滑金属导轨放置于磁感应强度大小为B、方向竖直向上的匀强磁场中,两导轨面高度差为H,导轨宽为L,导轨足够长且电阻不计,在导轨面上各放一根质量均为m、阻值均为R的匀质金属杆2和3。开始时两根金属杆位于同一竖直面内,杆与轨道垂直且处于锁定状态,现有一质量为m、阻值为R的金属杆1于金属杆2的左侧相距L处以水平速度v0向右运动,与金属杆2相碰(作用时间极短)并粘连一起,碰撞前瞬间同时解除杆2和杆3的锁定使两杆能沿导轨自由滑动,求:
(1)杆1向右运动L过程中通过杆1的电量q;
(2)杆1和杆2碰撞后瞬间的速度大小;
(3)整个运动过程中回路的感应电流产生的总焦耳热。
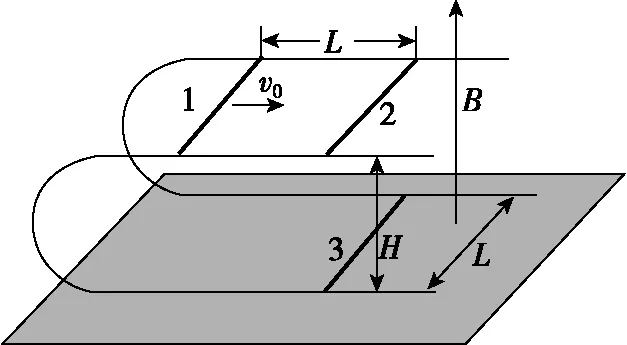
图7
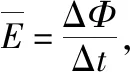
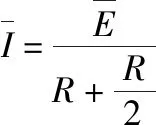
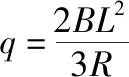
(2)对杆1任一极短时间Δt内应用动量定理得
-BIL·Δt=mΔv,即-BL·Δq=mΔv
由于在极短时间内上式均成立,故在杆1运动至碰撞前过程中也成立,则有
-BLq=mv1-mv0
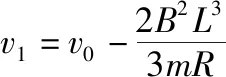
杆1和杆2碰撞瞬间,取杆1和杆2为系统,由动量守恒定律得mv1=2mv2
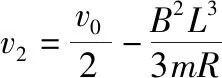
(3)杆1碰撞前在安培力作用下做减速运动,安培力做负功将棒的动能转化为电能,再通过电流做功将电能转化为内能,故焦耳热等于杆1的动能减少量,由动能定理得
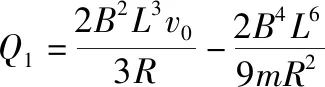
杆1和杆2碰撞之后在安培力的作用下,两杆做减速运动,杆3在安培力作用下做加速运动,当三杆速度大小相等时,回路内感应电流为0,之后三杆做匀速直线运动,根据动量守恒定律得
2mv2=3mv3
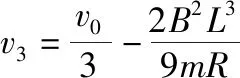
根据系统的能量守恒定律得
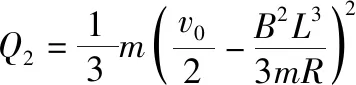
故整个过程回路产生的总焦耳热为
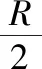
【方向4】三杆均放置于磁场内,同时切割磁感线。
【设计思路】设计三根导体杆放置于同一磁场或不同磁场内(如图8),赋予相同或不同的速度同时切割磁感线产生感应电动势。
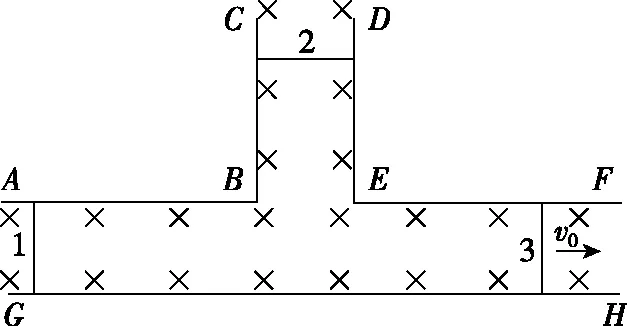
图8
【分析策略】三杆在磁场中同时切割磁感线时,产生三个感应电动势,模型会涉及三个电源的连接方式和三杆的动态分析问题,基于《考试大纲》的要求,试题的编制仍限定于电源串联方式的讨论。与双杆同时切割模型类似,在涉及动态分析时,要注意杆系统有外力作用和无外力作用的最终稳态问题。
【例4】如图9所示,三根光滑金属导轨ABC、DEF和GH水平固定,AB、EF平行于GH,BC平行于DE,导轨间距均为L,电阻不计,且整个导轨平面均处于竖直向下的匀强磁场中,磁感应强度为B。三根金属棒a、b、c垂直放置在导轨上,与导轨接触良好,其中a、b两金属棒质量均为m,电阻均为R,c金属棒质量为2m,电阻为2R,开始时金属棒a、b处于静止状态,给c棒初速度v0向右运动,假设轨道足够长,棒a只在轨道AB与GH上运动,棒b只在轨道BC与DE上运动。求:
(1)金属棒a、b、c最终稳定的速度分别为多少;
(2)金属棒a从开始运动到最终稳定所产生的热量;
(3)在三根金属棒的整个运动过程中金属棒a、b、c与水平导轨围成面积的变化量。
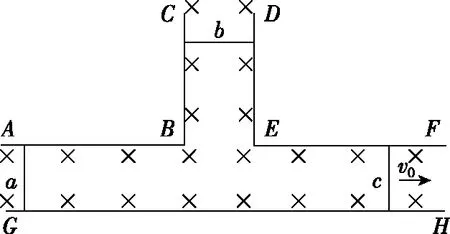
图9
【解析】(1)导轨光滑,所以在运动过程中a、b、c不受摩擦力作用,在水平方向只受安培力,棒c以初速度v0向右运动,则回路产生逆时针方向电流,c受向左的安培力,a受向右的安培力,b受安培力方向沿CB方向,所以a、b均开始做加速运动,c做减速运动,a、b产生的感应电动势与c方向相反,当三者产生的感应电动势互相抵消时,回路电流为零,达到稳定平衡状态,三棒同时开始做匀速运动,故最终稳定时Ec=Ea+Eb,即BLvc=BLva+BLvb①
对金属棒a,根据动量定理得BLqa=mva-0 ②
对金属棒b,同理得BLqb=mvb-0 ③
对金属棒c,同理得-BLqc=2mvc-2mv0④
由于a、b、c始终串联,故qa=qb=qc
联立②③得vb=va⑤
(2)取金属棒a、b、c为系统,根据系统的动能定理得
由于通过金属棒的电流相同,故产生的热量与电阻成正比,得
(3)取金属棒a,由动量定理得BLq=mva,得
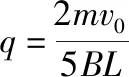
【点评】多轨多杆问题的分析重点在于注意金属棒的动态运动过程,明确在自由滑动的条件下金属棒都匀速运动时回路中总电动势为零,要了解多个电源在电路中的连接特征,知道运用动量定理是求电磁感应中电量、动能定理是求热量的常用思路。

