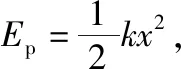聚焦高考动量与能量疑难问题
2019-07-08浙江
浙江
高考中与动量、能量相关联的综合计算题,涉及动量定理、动量守恒定律、能量守恒定律、动能定理等主干规律,是高考的热点课题、备考的难点板块,具有模型多重、情景多变、过程多样、知识考点综合性强、思维能力要求高、易错区分度高等特点,突出对物理建模能力、过程分析能力、规律应用能力、归纳推理能力及数学运算能力的考核。现选取三类与动量、能量相关联的典型试题,进行探析与解剖。
一、以反冲运动为模型的动量与能量问题
反冲运动是动量守恒的一个特例,是原来静止的一个物体在内力作用下分裂为沿反向运动的两个物体。发射火箭、人船运动是最为基础、典型的一维直线反冲案例,较为复杂的是二维平面内类反冲运动问题。
【例1】如图1所示,质量M=3 kg的滑块套在水平固定着的轨道上并可以在轨道上无摩擦滑动,质量m=2 kg的小球通过长L=0.75 m的轻杆与滑块上的光滑轴O连接。开始时滑块静止,轻杆处于水平状态,现给小球一个v0=3 m/s的竖直向下的初速度,不计空气阻力的影响,小球与滑块均可视为质点,g取10 m/s2,求:
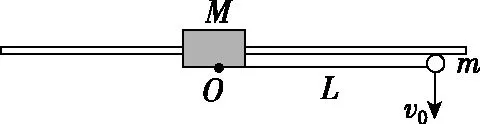
图1
(1)小球第一次运动到最低点时,滑块沿轨道向右移动的距离;
(2)小球第一次运动到最低点时,轻杆对小球的作用力的大小;
(3)小球相对于初始位置而言,可以上升的最大高度。
【解析】(1)小球从初始位置下摆到最低点的过程,球与滑块组成的系统水平方向所受合力为0,在水平方向由平均动量守恒得
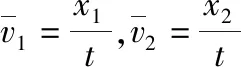
整理得mx1-Mx2=0
其中小球与滑块相对地面的水平位移大小之和等于它们水平方向上的相对位移,即有x1+x2=L
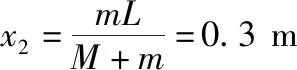
即滑块沿轨道向右移动的距离为0.3 m
(2)小球第一次摆到最低点时,设其速度大小为v1,滑块速度大小为v2,在最低点由系统水平动量守恒得
mv1-Mv2=0
小球下摆过程系统由机械能守恒定律得
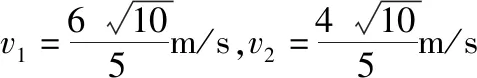
小球在最低点,由牛顿第二定律及向心力公式得
(3)设小球相对初始位置可上升的最大高度为h,此时小球在竖直方向的速度vy=0,根据系统水平动量守恒得
(M+m)vx=0
得此时小球与滑块在水平方向的速度均为vx=0
解得h=0.45 m
【疑难点】本题属于轻杆连接体系统的类反冲运动,深度融合了动量与能量、牛顿第二定律与圆周运动的考核。教与学中的疑难点主要有:
(1)不知晓系统仅在水平方向所受合力为0,仅在水平方向动量守恒,不能列出水平平均速度与水平位移的关系式;不知道两物体相对地面的水平位移大小之和等于它们水平方向上的相对位移;
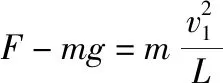
(3)不能推解系统中小球与滑块的末速度、末动量为0,不能正确列出系统在初、末状态能量守恒的关系式。
【规律点】求解二维平面内类反冲运动物体的速度、位移、受力、功能等问题,须领悟以下几个基本规律点:
(1)熟悉并理解类反冲运动在水平方向上动量守恒,根据动量守恒定律推得水平速度与水平位移大小的关系式mv1=Mv2,mx1=Mx2,其中x1+x2=L相对;
(2)针对类反冲运动的不同过程,能灵活应用动量守恒定律、机械能守恒定律或能量守恒定律、动能定理列方程组,求解相关结果;
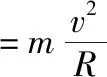
二、以弹性碰撞为模型的动量与能量问题
如果碰撞过程中机械能守恒,这样的碰撞称为弹性碰撞。钢球、玻璃球之间的碰撞,能量损失都很小,可视为弹性碰撞。
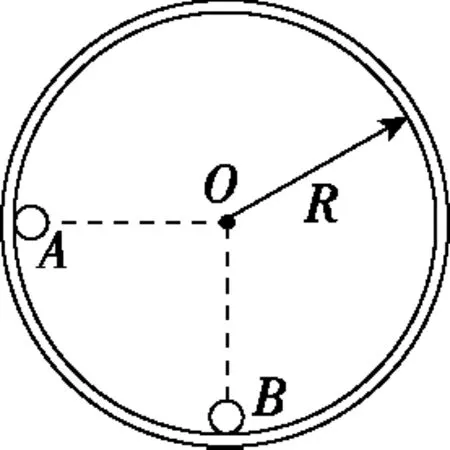
图2
【例2】如图2所示,半径为R=0.8 m的内壁光滑圆形轨道固定在竖直平面内。小球A从左侧与圆心等高处由静止释放,并与静止于轨道最低点的小球B发生第一次碰撞,这次碰撞及以后的所有碰撞过程中均无机械能损失。小球A、B均可视为质点,质量分别为mA=1 kg、mB=3 kg,重力加速度g取10 m/s2。求:
(1)第一次碰撞刚结束时小球A、B各自的速度;
(2)第一次碰撞过程A球对B球的冲量及所做的功;
(3)试讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度。
【解析】(1)小球A下滑过程,由机械能守恒定律得
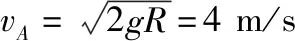
设A、B第一次碰撞后的速度大小分别为vA′、vB′,并以水平向右为正方向,由动量守恒定律得
mAvA=mAvA′+mBvB′
两球发生弹性碰撞,由机械能守恒定律得
代入数据,解得
vA′=-2 m/s,方向水平向左
vB′=2 m/s,方向水平向右
(2)第一次碰撞过程,设A球对B球的冲量为I,所做的功为W,对B球由动量定理得I=mBvB′-0
解得I=6 N·s,方向水平向右
解得W=8 J
(3)以水平向右为正方向,根据机械能守恒可知,小球A、B在轨道最低处第二次碰撞前的速度为
vA′=2 m/s(方向水平向右)
vB′=-2 m/s(方向水平向左)
设它们第二次碰后的速度分别为vA″、vB″,由动量守恒定律得
mA(vA′)+mB(vB′)=mAvA″+mBvB″
由机械能守恒定律得
代入数据,解得
vA″=-4 m/s,vB″=0
(另一组解,不合题意,已舍去)
即小球A、B在轨道最低处第二次碰撞刚结束时,小球A的速度大小为4 m/s,方向水平向左,小球B静止。
由此可知,第3次碰撞前的情形,与第1次碰撞前的情形相同,由此归纳可得:
当n为奇数时,小球A、B在第n次碰撞刚结束时的速度,分别与其第一次碰撞刚结束时相同,即vA′=-2 m/s,方向水平向左;vB′=2 m/s,方向水平向右。
当n为偶数时,小球A、B在第n次碰撞刚结束时的速度,分别与其第二次碰撞刚结束时相同,即vA″=-4 m/s,方向水平向左;vB″=0,球B静止。
【疑难点】本题属于多过程“一动一静”型与“对向互动”型弹性碰撞,深度融合了动量守恒与能量守恒的考核。教与学中的疑难点主要有:
(1)物理素养不扎实。如不能列出弹性碰撞的动量守恒与机械能守恒的关系式,不能理清第二次碰撞前动量与速度的方向,缺乏速度与冲量方向的说明;
(2)数学基础不牢固。不能快速、顺利求解动量守恒与机械能守恒的方程组;
(3)归纳能力较欠缺。不能按n为奇数或偶数进行分类讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度。
【规律点】有关同一直线的弹性正碰,把握并领会以下几个基本规律点,有助于快速列式与求解:
(1)明晰两大守恒。两物体间的弹性碰撞过程,动量与机械能(动能)同时守恒;
(2)洞悉经典模型。运动的A球与静止的B球发生弹性碰撞的关系式:
mAvA=mAvA′+mBvB′
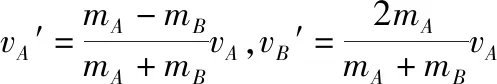
(3)知晓一个特例。质量相等的A与B发生弹性碰撞,速度相互交换,即vA′=vB,vB′=vA。
【例3】如图3所示,一长L=10 cm的轻质细绳一端系一质量为m=50 g的小球A,另一端固定在光滑水平轴O上,小球跟水平面接触但无相互作用,在球的两侧等距离处分别固定一个光滑的斜面和一个挡板,斜面底端与挡板间的距离s=2 m,水平面的动摩擦因数为μ=0.25。现有质量也为m=50 g的滑块B,从斜面上高度h=5 m处静止滑下,与小球发生弹性正碰。不计滑块与小球、挡板碰撞时机械能的损失,忽略空气阻力的作用,滑块和小球均可视为质点,重力加速度g取10 m/s2。

图3
(1)求滑块与小球第一次碰前的速度以及碰后的速度;
(2)求滑块与小球第一次碰后瞬间绳子对小球的拉力大小;
(3)滑块与小球碰撞后,小球在竖直平面内做圆周运动,求小球做完整圆周运动的次数。
【解析】(1)设滑块与小球碰撞前后的速度分别为v1、v1′,小球碰撞后的速度为v2′,对滑块应用动能定理得
B与A发生弹性碰撞,由动量守恒定律得
mv1=mv1′+mv2′
碰撞过程由机械能守恒定律得
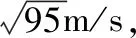
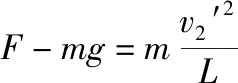
代入数据,得绳子拉力F=48 N
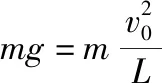
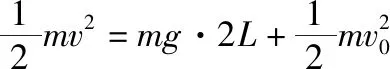
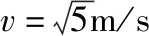
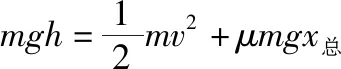
代入数据,解得x总=19 m
此过程中滑块与小球碰撞的次数为
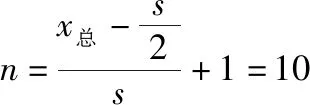
即小球做完整圆周运动的次数为10次。
【疑难点】本题属于等质量的滑块与小球多次弹性碰撞、速度多次相互交换的典型试题。教与学中的疑难点主要有:
(1)不知晓质量相等的物体发生弹性正碰时,具有速度相互交换的特点;
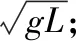
(3)不能发现滑块与小球的碰撞次数n与滑块运动的总路程x总、s之间的关系;
(4)不能发现滑块与小球弹性碰撞的次数就是小球做完整圆周运动次数的隐含关系。
三、以完全非弹性碰撞为模型的动量与能量问题
如果碰撞过程中机械能(动能)不守恒,这样的碰撞称为非弹性碰撞。木制滑块、橡皮泥球之间的碰撞,形变不能完全恢复,可视为非弹性碰撞。两个物体碰撞后以相同的速度运动或具有相同的速度,这样的碰撞称为完全非弹性碰撞。
【例4】如图4所示,水平光滑的地面上有一辆质量为M=3 kg的平板小车,质量为m=1 kg的小木块放置在平板小车的左端,它们一起以大小为v0=4 m/s的速度向右做匀速直线运动,小车与竖直墙碰后反弹,碰撞过程无机械能损失,木块最终没有从平板小车上滑落。木块与小车上表面之间的动摩擦因数为μ=0.5,重力加速度g=10 m/s2,不计空气阻力的影响,木块可视为质点。求:
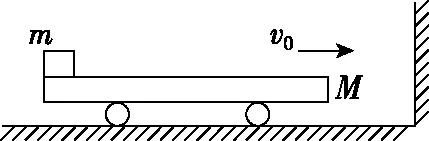
图4
(1)平板小车最终的速度;
(2)木块在小车上滑行的时间;
(3)平板小车至少多长?
【解析】(1)小车与墙壁碰撞后立即以速度v0向左运动,此时木块速度仍为v0向右,在碰撞后的运动过程中,小车与木块组成的系统动量守恒。以水平向左为正方向,则有
Mv0-mv0=(M+m)v
代入数据,解得v=2 m/s
则小车最后速度为2 m/s,方向水平向左。
(2)木块在摩擦力作用下相对于小车的滑动过程,同样以水平向左为正方向,根据动量定理有
μmgt=mv-m(-v0)
代入数据,解得t=1.2 s
(3)对小车和木块组成的系统,减少的总动能转化为内能,应用能量守恒定律及摩擦生热公式得
代入数据,解得L=4.8 m
即小车至少长4.8 m。
【疑难点】本题属于以木块与小车为背景,与动量规律和能量规律结合考核的典型试题。教与学中存在的疑难点如下:
(1)忽视矢量性,导致列式错误。如动量守恒Mv0+mv0=(M+m)v,动量定理μmgt=mv-mv0,都是不注意动量方向造成的错误式子;
(2)缺乏分析力,导致应用力弱。不清楚碰撞后小车和木块初态时的动量,也不清楚它们末态相对静止具有相同的速度,不清楚滑块受到摩擦力的方向,不具备综合运用动量守恒、动量定理与能量守恒三大规律求解问题的能力。
【规律点】完全非弹性碰撞模型的解读:
(1)速度特征。两个物体碰撞后以相同的速度运动或具有相同的速度,即m1v1+m2v2=(m1+m2)v;
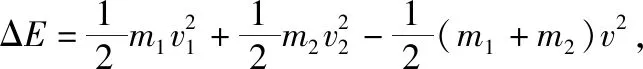
【例5】如图5所示,在水平面上依次放置小物块A和C以及曲面劈B,其中A与C的质量相等均为m,曲面劈B的质量M=3m,劈B的曲面下端与水平面相切,且劈B足够高,各接触面均光滑。现让小物块C以水平速度v0向右运动,与A发生碰撞,碰撞后两个小物块粘在一起又滑上劈B。物块A和C可视为质点,不计空气阻力,重力加速度为g,求:
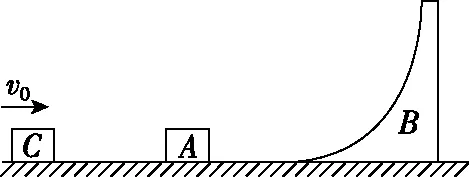
图5
(1)物块C与A碰撞过程中系统损失的机械能;
(2)粘合体AC在曲面劈B上能达到的最大高度;
(3)粘合体AC与曲面劈B的最终速度。
【解析】(1)物块C与A发生碰撞粘在一起,取水平向右为正方向,由动量守恒定律得mv0=2mv
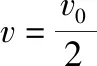
该碰撞过程系统损失的机械能为
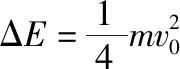
(2)碰撞后粘合体AC在曲面劈B上达到最大高度时三者速度相同,设为v′,最大高度为h,取水平向右为正方向,由水平方向动量守恒得
2mv=(2m+M)v′
此过程由系统机械能守恒得
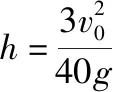
(3)设粘合体AC与曲面劈B的最终速度分别为v1、v2,由系统动量守恒与机械能守恒得
2mv=2mv1+Mv2
联解方程组得
【易错点】本题属于完全非弹性碰撞与弹性碰撞的深度考核,教与学中的疑难点在于碰撞建模能力的领悟:
(1)不能发掘粘合体AC在曲面劈B上达到最大高度时所隐含的速度相同的关系,即粘合体AC在曲面劈B上滑过程可视为类完全非弹性碰撞;
(2)不能洞悉粘合体AC与曲面劈B之间的作用过程,可视为类弹性碰撞,是最典型的一动一静弹性碰撞模型。
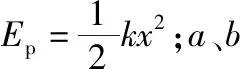
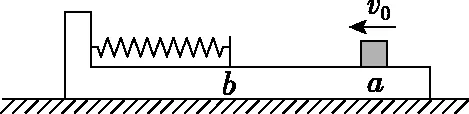
图6
(1)求弹簧被压缩最短时小物块的动量大小;
(2)求小物块与长木板上表面间的动摩擦因数;
(3)试通过计算说明小物块最终停在长木板上的位置。
【解析】(1)当弹簧被压缩最短时,小物块与长木板达到共同速度v,选取向左为正方向,根据动量守恒定律有
mv0=(M+m)v
解得v=1.0 m/s
此时小物块动量大小p=mv=1.0 kg· m/s
(2)物块由a向b运动并压缩弹簧的过程,根据能量守恒定律可知,系统减少的动能转化为弹簧的弹性势能和系统的内能,则有
解得μ=0.50
(3)当小物块在长木板上停止相对滑动时,与长木板有相同速度,由动量守恒定律可得其共同速度仍为
v=1.0 m/s。
设小物块在长木板上向右相对滑行的距离为s右,在整个相对运动过程中,系统由能量守恒定律可得
解得s右=0.60 m
因s右=d+xm,故小物块最终停在木板上a点。
【疑难点】本题涉及弹性势能的定量计算是其最大亮点,教与学中的主要疑难点有:
(1)不知隐含状态中的速度关系。不能挖掘出弹簧弹性势能最大及末态时均隐含物块与木板速度相同的关系;
(2)不能明确块板作用中的等效模型。块板系统从初态到弹簧弹性势能最大时的状态及末态,均可等效视为完全非弹性碰撞;
(3)不能应用题意给定公式求解。对于题中给定的弹性势能公式,不能熟练应用于列式求解。
【规律点】含弹簧系统的动量与能量问题解读:
(1)多样性。一般涉及多个研究对象、多个物理过程及多种碰撞模型,可灵活选用动量定理、动量守恒定律、能量守恒定律、动能定理列式求解;
(2)守恒性。若系统所受合外力为0,则弹簧压缩到弹性势能最大时,系统内的物体具有相同的速度,并满足动量守恒与能量守恒;