基于MATLAB单摆运动的数值分析

马 堃

(黄山学院信息工程学院，安徽黄山245041)

单摆作为简谐振动的一种物理模型，几乎在每一本大学物理教材中都会介绍[1-2]。但由于其动力学方程的非线性特点，在教学过程中往往只研究其小摆角的情况，此时动力学方程简化为线性方程，其解为一余弦函数。而对于大摆角单摆的运动状态随时间的演化规律，如何在大学本科阶段讨论单摆振动时的物理规律是大学物理力学部分一个教学难点。早在1984年，赵炳林先生就对单摆振动的严格周期进行了分析，将积分方程中的被积函数进行级数展开，从而得到精确的级数解[3]；随后，人们探索了多种近似算法，如线性插值[4]、格林函数[5]、冲击波解[6]等。随着计算机的普及以及数学计算软件的发展，人们在教学过程中逐渐探索利用数学计算软件辅助复杂公式和方程的求解[7-8]。然而，这些研究主要集中在单摆的周期计算上，对非线性单摆的摆动和能量转化等情况讨论的较少。本文利用MATLAB软件对单摆非线性运动进行研究，通过线性近似处理，讨论非线性单摆与线性单摆运动状态、能量以及周期随时间演化的特点。

1 理论模型

设一单摆的摆长为l，摆球质量为m，阻尼系数为γ，则其满足的动力学微分方程可以写成为

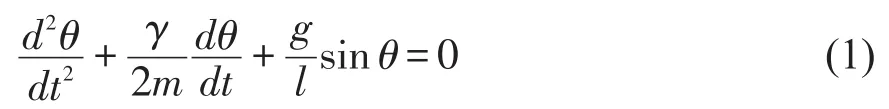
其中θ是单摆偏离平衡位置的角位移，上式是一个非线性微分方程，该方程无严格的解析解。当单摆做小角度摆动时，有sinθ≈θ关系，从而方程(1)可以简化为一个线性微分方程，即

当γ=0时，即无阻尼振动，(1)式进一步退化为

上式即为线性单摆所满足的动力学方程，该方程及其解在一般的教科书上都有。由于微分方程(1)式中非线性项sinθ的存在，无法给出其解析解。为此，本文采用数值求解方法中的四阶龙格-库塔法[9]对方程进行求解。首先对二阶微分方程作降阶处理，令̇，则(1)式可以降阶为一阶微分方程组，即

对于上式，在给定初始条件y1(t=0)=θ0，y2(t=0)=0的情况下，可以按照四阶龙格-库塔法的计算方法，读者可以自行编写计算程序，也可以直接调用现有的程序包进行计算，本文以MATLAB软件为例，调用“ode45”命令进行求解，具体编写程序如下：

F=@(t，y)[y(2);-g/L*y(1)-gamma/2/m*y(2)]%定义方程组(4)式

[t，y]=ode45(F，[0：0.001：20]，[theta0，v0]);%利用四阶龙格-库塔法求解，解赋值给[t，y]

本文将利用上面的MATLAB程序分别对线性摆和非线性摆进行数值计算，并对计算结果进行分析。方便起见，在计算中取m=1，l=1，g=9.8，均为国际单位。

2 线性近似下的单摆振动

2.1 运动学方程

在线性近似下，只需要将一阶微分方程组(4)中的siny1用y1代替即可。初始角位移和初始角速度分别取θ0=π/36和ω0=0，利用四阶龙格-库塔法可以得到单摆线性振动时的数值解，分别是角位移y1=θ和角速度。图1给出了阻尼系数在0～1范围内单摆角位移随时间的演化规律。从图中可以看出：无阻尼时，单摆的作等振幅振动；有阻尼时，振幅随着时间的推移逐渐衰减，且随着阻尼系数的增加，衰减的越来越快。同时，我们发现虽然在有阻尼下单摆的振幅逐渐减小，但其摆动的周期仍然为一定值。

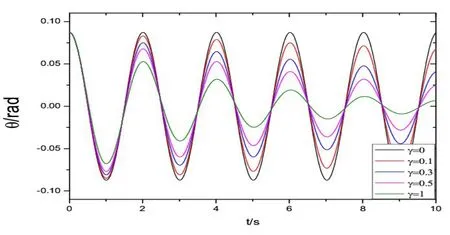
图1 线性近似下单摆作摆动的角位移

2.2 机械能

根据角位移y1=θ和角速度y2=θ̇，可以进一步得出单摆摆动过程中能量随时间的演化情况。取单摆摆动最低点时为势能零点，初始动能为Ek0=0 ，则初始时刻势能为Ep0=mgl(1-cosθ0)，初始时刻总机械能为E0=Ek0+Ep0=mgl(1-cosθ0)，在单摆摆动过程中任意时刻的势能为

图2分别给出了线性单摆动能、势能和总机械能随时间演化情况，其中图2(a)是无阻尼情况，图2(b)是阻尼γ=0.5时的情况。可以看出动能、势能和机械能均在周期性变化，动能增加，势能减小，两者相互转化，周期值始终保持不变。仔细分析图2(a)可以发现，系统的总机械能会随着时间演化而稍有波动，且随着摆角的增加波动的越大。总机械能的波动意味着机械能不再“守恒”。当然，这并不是真的机械能不守恒，而是由于对微分方程(1)作了线性近似导致的。

图2 线性近似下单摆的机械能

3 非线性单摆的振动

3.1 运动学方程

下面我们将采用严格的数值求解，给出非线性微分方程(1)式的解，并讨论非线性单摆运动过程中角位移和机械能等物理量的演化规律。

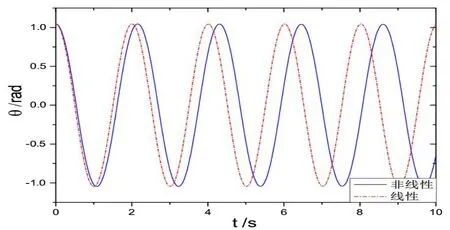
图3 线性近似和非线性摆动时角位移对比

图3给出了初始角位移θ0=π/3无阻尼单摆振动的角位移随时间的变化关系，其中实线是非线性求解的结果，点划线是线性近似下的结果。可以看出，无阻尼时，无论是线性单摆，还是非线性单摆均做等振幅摆动，非线性摆动周期比线性摆动的周期大，即非线性摆随着时间的推移摆动越来越慢。

图4 非线性单摆的角位移

图4给出了不同初始角位移下非线性单摆的角位移随时间演化情况，其中图4(a)是无阻尼摆动，图4(b)是阻尼摆动，其阻尼系数γ=0.5。从图中可以看出，振动周期随着初始角位移的增加而增大，周期随着时间推移逐渐减小，且在相同初始角位移情况下，无阻尼振动的周期大于有阻尼振动的周期。这是由于系统受到外界阻尼的影响，能量逐渐耗散，单摆摆动的振幅也越来越小，阻尼系数越大，振幅衰减的越快。

3.2 机械能

图5给出非线性单摆动能、势能和机械能随时间演化的情况，其中图5(a)是无阻尼摆动，图5(b)是阻尼摆动。无阻尼时，动能和势能相互转化，此消彼长，但系统的总机械能保持不变，等于系统初始的机械能，满足能量守恒定律，这一点与线性摆不同。有阻尼时，动能和势能与会随着时间相互转换，但由于阻尼的存在，在转换的过程中，总机械能随着时间推移而逐渐较小。

图5 非线性单摆的机械能

3.3 周期

可以看出，线性单摆的周期只与摆长有关，与初始角位移无关，而非线性单摆的周期不仅与摆长有关，还与初始的角位移有关。表1给出了不同初始角位移下非线性单摆的周期，其中T表示本文数值计算得到的结果，T0表示线性摆周期，Ref[T/T0]表示(8)式计算的结果。从该表中可以看出，随着初始角位移的增大，单摆的周期增大，且阻尼振动的周期小于无阻尼时的周期。通过与严格的积分形式解(8)式的结果比较可见，本文数值计算的结果与(8)式结果的误差均在0.3%之内。

表1 不同初始角位移下非线性摆的周期

图6给出了单摆的摆动周期与初始角位移之间的关系，其中虚线表示线性近似下的结果。在线性近似下，单摆的周期与初始角位移无关，是一个定值。图中可以看出非线性摆的周期与不仅与初始角位移有关，而且与阻尼有关。初始角位移越大，周期越大，阻尼越大，周期越小。

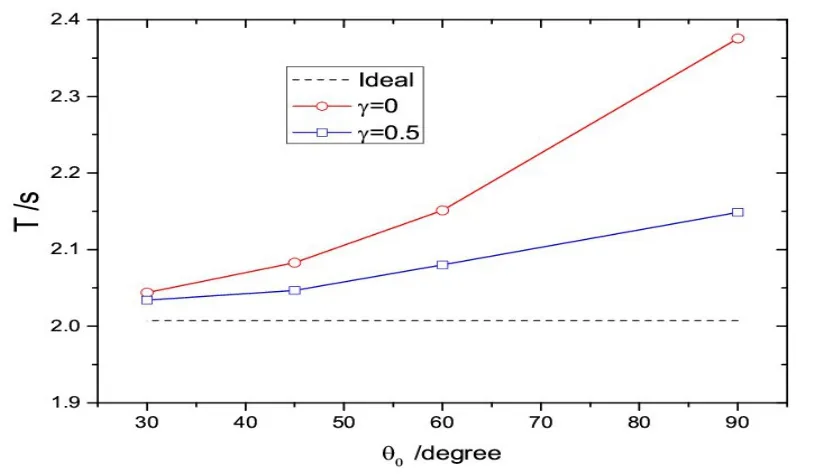
图6 单摆周期与初始角位移的关系

4 总结

本文利用四阶龙格-库塔法严格求解单摆的非线性动力学微分方程，讨论了非线性单摆的角位移、能量和周期随时间的演化规律。在非线性解下，单摆的机械能不再随着时间发生变化。虽然本文的分析是基于数值求解方法，但是随着计算机的普及以及数学计算软件的发展，我们认为有必要、也有条件在大学本科阶段普及数值计算方法，以帮助加深对物理概念的理解，拓展学生运用所学知识解决实际问题的能力。