一种高效的无角度约束移动机器人路径规划方法
2019-07-05杨建禹白国振
杨建禹,白国振
(上海理工大学机械工程学院,上海200093)
移动机器人路径规划问题是指在有障碍物存在的地理环境中,如何寻找一条从给定起点到终点的路径,使机器人沿该路径移动的过程中不与障碍物发生碰撞且路程最短或移动代价最小。国内外学者在该问题上做了大量的研究,在众多的路径规划算法中采用栅格化地图的方法,由于其模型简单且方便建立,从而得到广泛的应用和发展,同时栅格化的地图经常作为即时定位与地图构建(SLAM)算法的结果输出形式[1]。在栅格化地图的应用方面,中国目前有曲道奎提出的将A*与人工势场相融合的方法[2]、杨晶东等提出的移动机器人行为融合的避障方法[3]、叶炜垚提出的基于虚拟障碍物与实际障碍物融合的方法[4],均取得了一定的效果。
国外基于栅格化地图移动机器人路径规划方面有Dijkstra[5]和A*[6]等适合处理静态地理环境的方法;同时还有D*[7],Focused D*[8],D* Lite[9]等适合应对动态地理环境或未知地理环境的方法,但是上述这些算法所获得的路径在真实的连续环境中却不是最优的路径。大多数情况下,这些算法所得路径上某两点间的路径还可以用两点间的直线来代替,这是因为这些算法均采用了固定角度步长(π/4)的方式向其相邻节点传递固定的路径里程信息,导致其获得的路径中转向点处路径转过的角度一定是π/4的整数倍,从而约束了最优路径的选择。为解决该问题,国际上又出现了一类无角度约束路径规划(any-angle path planning)算法,典型的有Field D*[10],Theta*[11],Block A*,Cwave[1]等。但是,这些算法中,有的运算速度慢,有的需要前期预处理,有的又过于复杂。为解决该问题,本文提出了一种易于实现且运算高效的路径规划方法WG(wave gate)。
1 基本符号和定义
1.1 符号约定
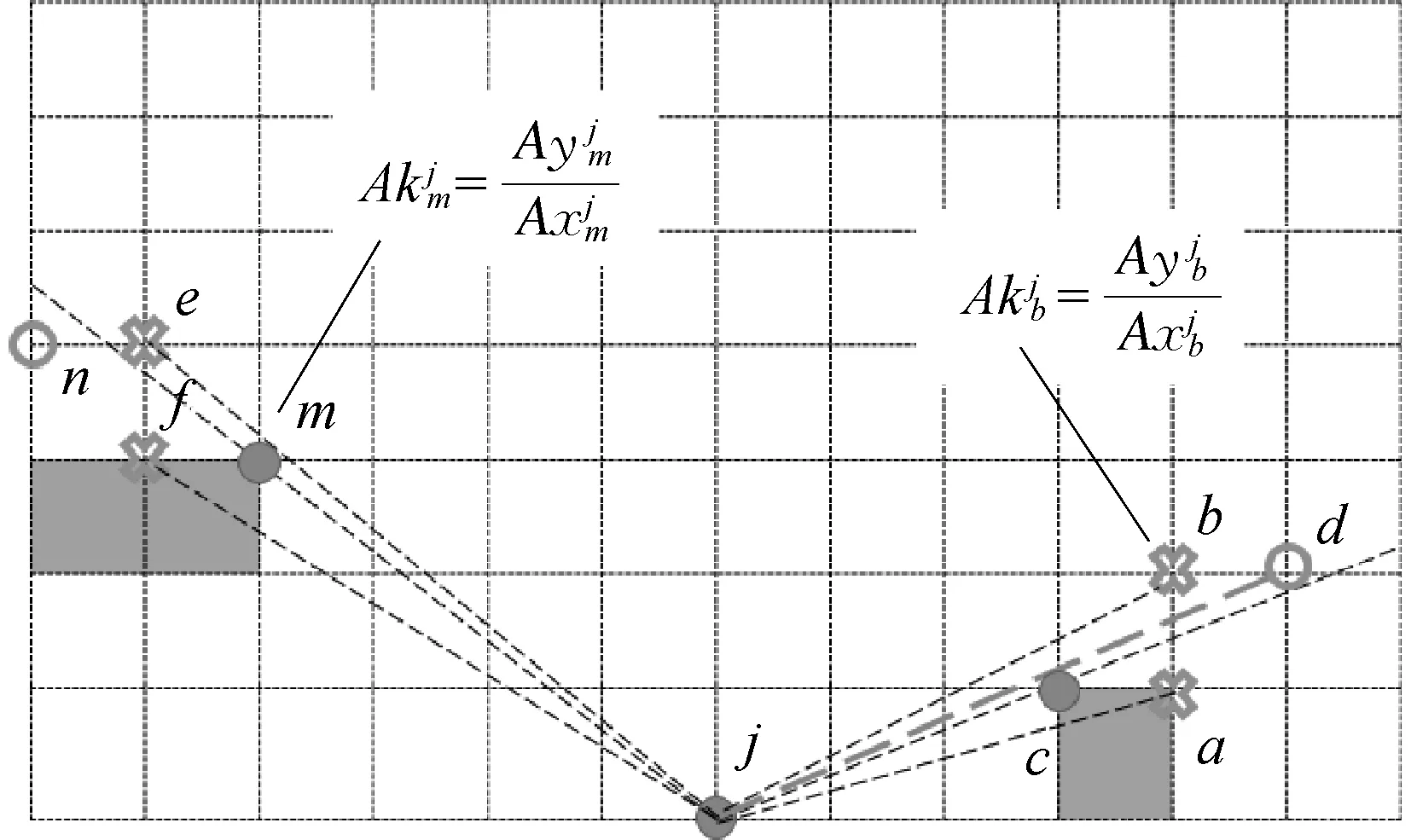
栅格地图M中所有栅格上的点组成1个集合,记为set-m(map)。定义由起始节点向终点不断搜索的过程中,某时刻已经被算法遍历的节点所组成的集合,记为set-c(close);而地图上未被遍历的节点集合,记为set-v。由set-c中全部节点构成的区域称作已遍历区域,用area-set-c表示;由set-v中全部节点构成的块区域,称作待遍历区域,用area-set-v表示。set-c中位于area-set-c与area-set-v交界线上的所有节点所组成的集合,记为set-f(fringe),其中元素称作前缘节点。栅格化地图前缘节点示意如图1所示,area-set-v与area-set-c的交界线上所有的节点都以“X”形符号标出,它们即为此时的前缘点,节点a,t,m均属于set-f(灰色区域表示为障碍物区)。
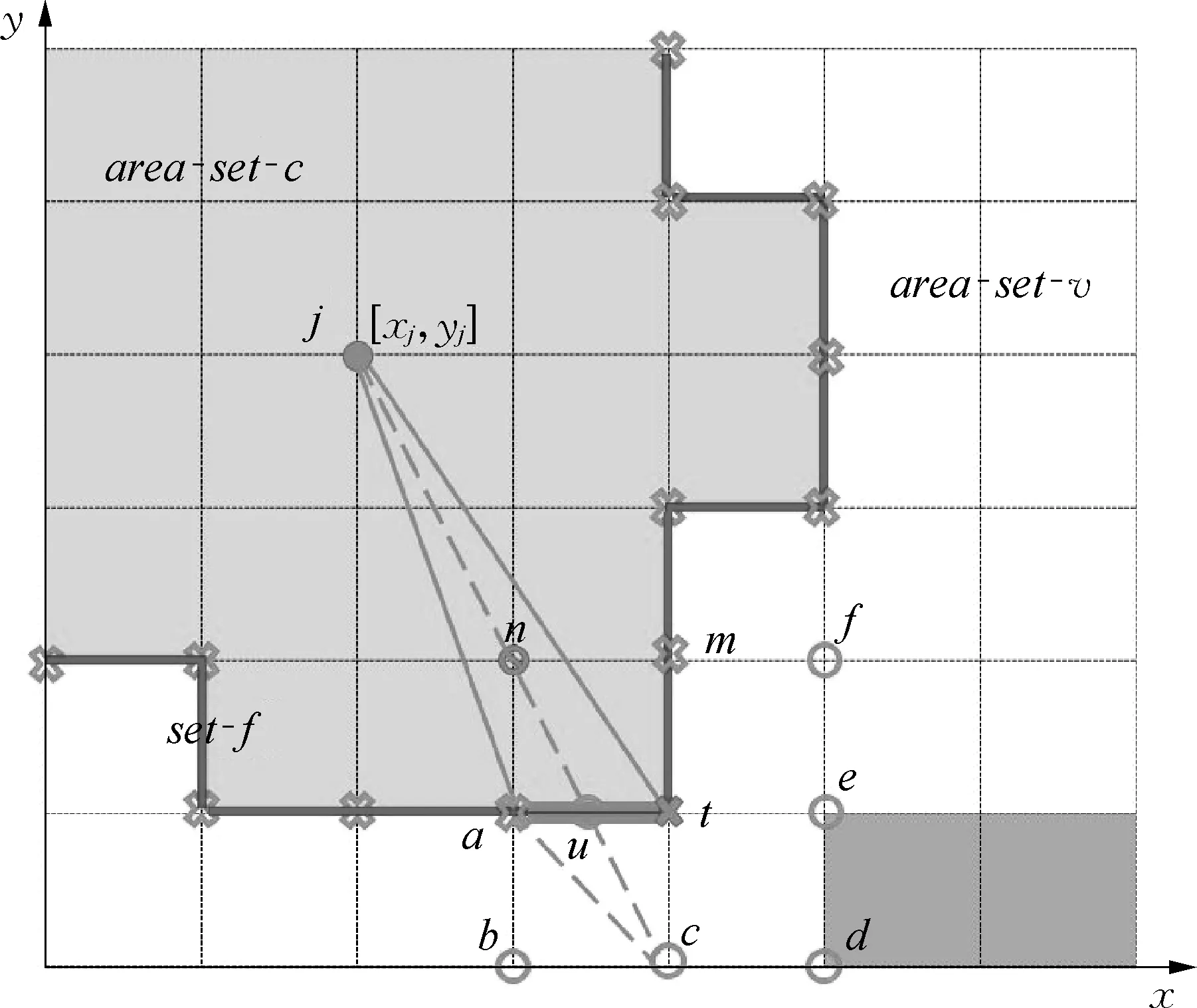
图1 栅格化地图前缘节点示意
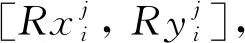
(1)
同时记
(2)
(3)
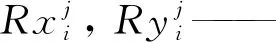
位于栅格地图M中的任意节点v均定义1个父节点,记为P(v)。在算法执行的过程中,节点v到地图上起点s的优化路径可由v到P(v)的直线与P(v)到s的优化路径组合而成。所以算法最终求得的路径可由终点g开始向其父节点进行迭代性的连线,即父节点再向父节点的父节点进行连线,直至迭代到起点s时为止而得到。在算法初始化时,地图上除起始节点的父节点定义为节点本身外,其他所有节点的父节点都定义为无穷大。同时,定义任意节点i到起始点的距离为Gi,若P(i)=j,由父节点的定义有:
Gi=Gj+Di-j
(4)
式中:Di-j——节点i到节点j的直线距离。
按式(5)定义评价函数K(i),其中i为地图上任意节点,并从集合set-f中选择评价函数数值最小的节点t作为拓展基点,即K(t)=min(K(i)),记cv=t,由该节点将产生新的前缘节点:
K(i)=Gi+Di-g
(5)
式中:Di-g——节点i到终点g的直线距离。
1.2 栅边节点
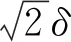
假设搜索算法已经完成了节点t的计算,并以节点t为基础拟求出其所有邻近节点中未被算法遍历过的节点距离数据,此时称节点t为栅边基点,记为gv此时有gv=t,并称t节点的父节点,即P(t)为set-ngb(t)任意元素的备选父节点,记为cp,则此时有cp=P(t),用函数形式表示为
cp=CP(gv,vi)
(6)
式中:vi——set-ngb(t)中未被算法遍历过的任意元素;CP(gv,vi)——以gv为栅边基点时求取节点vi的备选父节点的函数。
set-ngb(t)中未被算法遍历过的元素vi与节点P(t)(即节点vi的备选父节点CP(t,vi))构成的线段Lvi-cp必然与节点vi的某条邻近栅边相交,则称该邻近栅边为节点vi在t为栅边基点时的栅边,组成该栅边的节点称为节点vi在t为栅边基点时的栅边节点,其中与节点vi构成对角关系的栅边节点记为v1,另外1个栅边节点记为v2,同时记:
(v1,v2)=Get_gate(t,vi)
(7)
图1中已知P(a)=P(t)=j,显然可知当t节点为栅边基点时,set-ngb(t)中节点c的两栅边节点分别为a节点(v1)与t节点(v2)。
定义set-m中任意节点v有set-ngb(v)中任意未被算法遍历的元素vi;以节点q为栅边基点时,相应的栅边节点v1与v2组成的栅边Lv1-v2与Lvi-cp(其中cp=CP(q,vi))的交点与节点vi若存在直通路径,即该交点与vi的连线不穿越障碍区域时,称Lvi-cp能穿越Lv1-v2,记为
Lvi-cp>>Lv1-v2
(8)
反之若该交点与vi不存在直通路径时即该交点与vi的连线穿越障碍区域时,称Lvi-CP(vi)不能穿越Lv1-v2记为
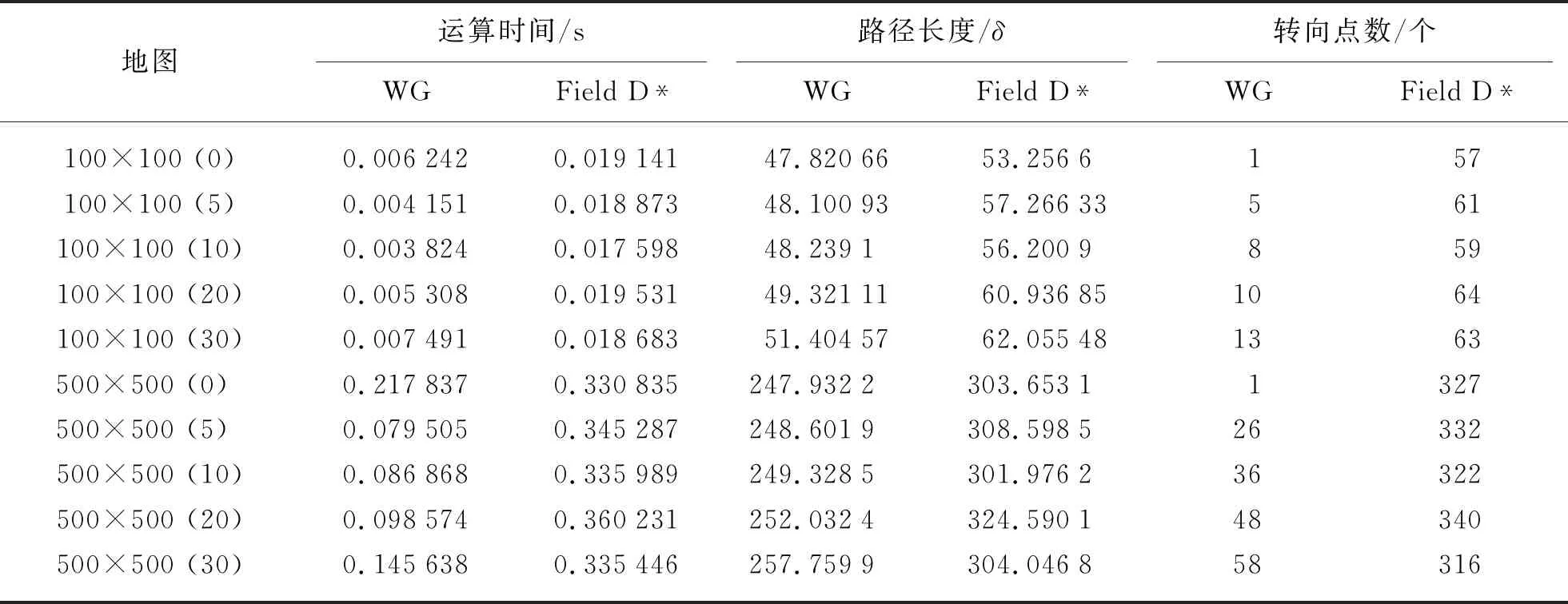
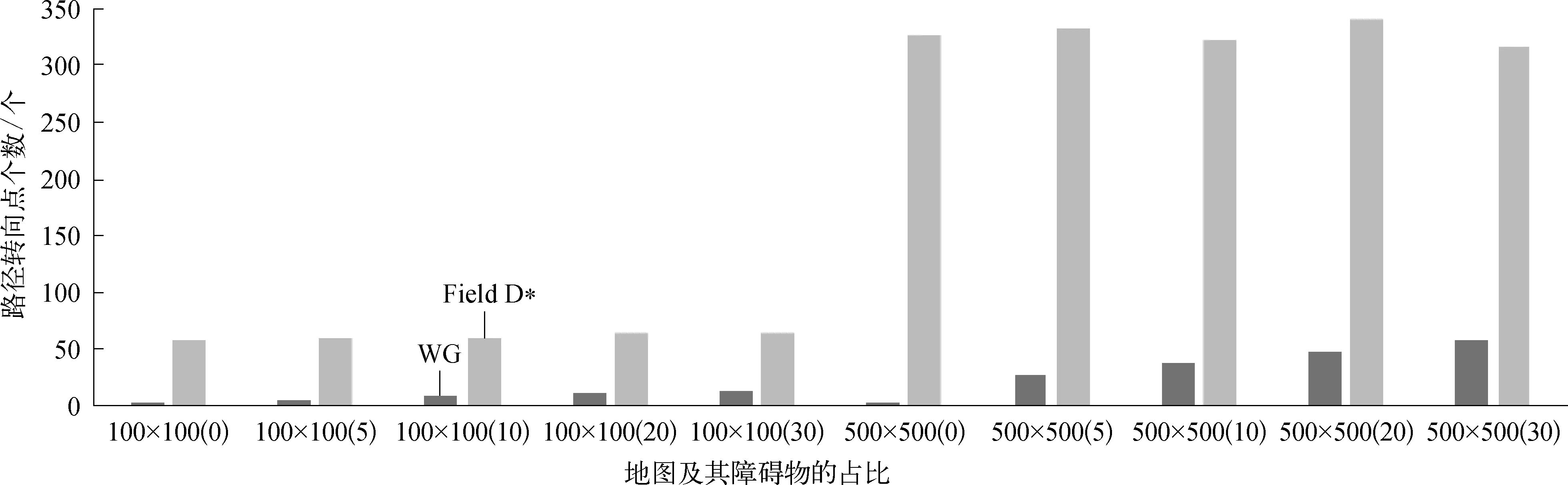
Lvi-cp> (9) 显然对set-ngb(v)中任意节点vi,其栅边节点v1与v2若满足P(v1)=P(v2)=CP(v,vi),且满足Lvi-cp>>Lv1-v2则必有: P(vi)=CP(v,vi)=P(v1) (10) 即节点v1与v2的父节点P(v1)与节点vi间必然存在直通路径。如图1中以a节点为栅边基点时,求得c的栅边为La-t,其与Lj-c交点为u,又已知P(a)=P(t)=CP(a,c),且交点u与节点c间的连线不穿越障碍区域,即Lc-cp>>La-t,则必然有P(c)=CP(a,c),这与栅格地图M中的实际情况相符。 依据式(1)和(2),当节点v为栅边基点时: 1)∀vi∈set-ngb(v)若满足式(11)的条件,则对应的节点称为节点v的第二类邻近节点。 (11) 2)∀vi∈set-ngb(v)若满足式(12)的条件,则对应的节点称为节点v的第一类邻近节点。 (12) 3)∀vi∈set-ngb(v)若满足式(13)的条件,则对应的节点称为节点v的第零类邻近节点。 (13) 对于不满足式(11)~(13)条件的节点,本文不进行讨论。式(11)~(13)中假定横向栅格间距等于纵向栅格间距。 对于节点v的第二类邻近节点vi,显然节点v与vi必为对角关系,故v必为节点vi的栅边节点,且v1=v,而对于v2的坐标[xv2,yv2]可由下式求得: (14) 障碍物形成的分界线附近的节点间的位置关系如图2所示。图2中假设节点j为起点,图中灰色阴影部分为障碍物,为实现节点到起始节点j的路径最短的要求,显然过节点j与节点c的直线lj-c将该直线附近的节点的父节点划分成节点j与节点c。即从节点j到节点c的方向上,自节点c以后位于直线lj-c上或上方的节点vi都有P(vi)=j,如P(b)=j;同样,该方向上自节点c以后位于lj-c下方的lj-c附近的节点vi都有P(vi)=c,如P(a)=c。该类节点通常满足P(v1)=P(P(v2))或P(v2)=P(P(v1)),例如以节点a为栅边基点时,节点d的栅边节点v1=a,v2=b,且明显有P(b)=P(P(a))=j。 图2 障碍物形成的分界线附近的节点示意 (15) 记满足式(15)的节点vi的两个栅边节点对应的父节点,即P(v1)与P(v2)中距离vi近的父节点为p1,另外一个节点为p2。例如图2中对于节点d有p1=c,p2=j。同时容易证明,若节点vi的两栅边节点满足Lvi-cp>>Lv1-v2,即Lvi-cp能穿越Lv1-v2时,节点vi的父节点可按下述方法确定: 首先节点vi位于分界线lp2-p1上,则P(vi)=p2;其次若节点vi与节点v1位于lp2-p1的同一侧,则P(vi)=P(v1);最后若节点vi与节点v2位于lp2-p1的同一侧,则有P(vi)=P(v2)。由式(3)可知,当vi位于分界线lp2-p1上时,可用函数的形式表达为 (16) 同样由式(3)可知,节点vi与节点v1位于lp2-p1的同一侧,不包括v1位于lp2-p1上的情况,用函数的形式表达为 (17) 同理可知,节点vi与节点v2位于lp2-p1的同一侧,不包括v2位于lp2-p1上的情况,用函数的形式表达为 (18) (19) 同理,式(17)与式(18)可分别等效为 (20) (21) 综上所述,满足式(15)且同时满足式(8)的节点vi的父节点,可依据式(22)确定: (22) 式(22)中,依次用式(19)~(21)等效替代式(16)~(18),主要是考虑移动机器人上工作的大多数嵌入式系统在处理乘法时的速度比除法要快许多。 定义函数(Gtemp,Ptemp,Ktemp)=UpdateVertice(vi,gv),其中节点vi为待更新节点,gv为更新vi节点的栅边基点。先由栅边基点gv求出vi的两栅边节点v1和v2,对于满足Lvi-cp>>Lv1-v2的节点可依据式(10)和(22)分别确定其父节点;对于Lvi-cp> 1)在前缘节点的集合set-f中选择满足K(t)=min(K(i))的节点t为拓展基点,即cv=t。从set-ngb(t)中依次选择已经被算法遍历过的节点q作为栅边基点,调用节点更新函数UpdateVertice(t,q)求得Gtemp,Ptemp,Ktemp。若满足Gtemp 2)以节点t为栅边基点对set-ngb(t)中未被遍历的邻近节点vi进行分类,并按照第零类邻近节点、第一类邻近节点和第二类邻近节点,按由高到低优先级依次调用节点更新函数UpdateVertice(vi,t),并将计算结果更新到节点vi中,即G(vi)=Gtemp,P(vi)=Ptemp,K(vi)=Ktemp。 3)对于步骤2)中能确定父节点的节点vi,插入到set-f中供下次迭代时使用,同时将节点t从set-f中移除,并返回步骤1)继而进行下一次迭代,直到终点节点g从set-f中被移出,或K(t)为无穷大时终止迭代。 WG算法与Field D*算法在同样的地图环境中进行路径搜索的结果比较见表1所列,两种算法的代码都以C++写成,并在同一台主频为3.7 GHz的计算机上进行运算。每类地图的统计数据均由100幅随机生成的同类型地图运算后取平均所得,表1中地图名为100×100(5)的地图,表示地图大小为100×100的栅格,且地图中障碍物块的比例为5%。 表1 WG算法与Field D*算法比较 从表1中的统计结果中不难发现: WG算法较Field D*在求解路径所需的时间以及所求的路径上转向点的个数等指标上都有很大的进步。图3中直观地对比了两种算法在不同地图规模以及不同障碍物块比例的地图中的计算结果,可以看出WG算法在运算速度上有较大的优势。由于Field D*算法采用线性插值的方式进行路径信息的传递,所以需要消耗较大的计算资源;另外,由于实际的地图环境中,距离起点的路径长度分布基本不会在2节点间呈线性分布,所以Field D*求得的路径长度较理论最短路径还存在不少的优化空间。相比之下,因为WG算法是通过分析两栅边节点的父节点的特点来确定被计算的节点的父节点,所以从这个角度上看,WG求解出的路径长度也将优于Field D*;其次由于Field D*算法是在1个栅格内进行线性插值导致其求得路径上的转向点增多,图4中可以很明显地显示出了它的这个缺点。 图3 WG算法与Field D*算法运行时间和求得路径长度比较 图4 WG算法与Field D*算法求得路径上的转向点比较 综上所述,WG算法之所以能在计算速度、路径转向点以及路径长度上较Field D*有明显提高,主要得益于: 1)通过建立栅边节点的概念来简化算法在搜索无障碍区域时的计算速度,因为它仅需比较两栅边节点的父节点是否与栅边基点的父节点为同一节点即可。 2)建立“障碍物形成的分界线附近节点的父节点的确定”的方法,利用两栅边节点的父节点以及待计算节点在障碍物形成的分界线上的同侧关系,简化复杂的角度求解计算(Theta*算法)。 但是为加快搜索速度,算法在栅边节点的结构下引入A*算法中启发函数的思想,某些特殊情况下将导致算法在遍历部分节点时,存在栅边节点的父节点还未被定义的情况,该算法在初始化时,将所有节点的父节点均定义为无穷大。目前的解决办法是将这些栅边节点插入Set-f中,并赋予比较高的优先级,使其在下轮迭代中成为拓展基点。然而,在某些实际应用中可以不用这样处理,继而避免过多的节点被引入set-f而降低算法的搜索效率,这也是后续需要研究和优化的一个方向。其次由于建立栅边节点的过程中,通过式(14)来确定两个栅边节点中的v2的坐标,实际是利用栅边节点v1与被计算节点间的对角关系(假定地图上2个栅格方向上的栅格间距相等),即v1与被计算节点的连线与坐标轴夹角为45°的前提条件,从而很容易地确定出v2的坐标,然而该方法并不能适用于非正方形栅格的地图上,所以后续在非正方形栅格地图上的计算也是需要继续研究的问题。2 栅格地图上父节点的确定
2.1 邻近节点的分类和栅边节点的确定

2.2 障碍物形成的分界线附近节点的父节点确定

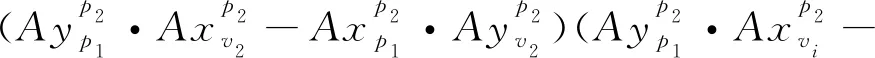
3 算法实现
3.1 节点更新函数
3.2 算法主要步骤
4 计算结果与比较

5 结束语
