孤岛工作面支承压力影响下顶板破坏机理研究*

王志强， 徐春虎， 任亚军， 仲启尧， 罗健侨， 苏泽华， 崔冬雪

(1.中国矿业大学(北京) 能源与矿业学院，北京 100083；2.中国矿业大学(北京) 共伴生能源精准开采北京市重点实验室，北京 100083；3.中国矿业大学(北京) 煤炭安全开采与地质保障国家级实验教学示范中心，北京 100083)

0 引言

采矿作业过程中，由于破坏了原岩初始应力状态，造成围岩应力重新分布；当围岩应力重新分布后，达到岩体的破坏极限，围岩出现变形、破坏。在长壁开采过程中，随着工作面的推进，在工作面前方形成超前支承压力，煤壁前方的支承压力使煤体裂隙扩展、贯通，并在煤壁一定深度范围形成塑性区，从而导致煤壁片帮，因此，在工作面回采过程中，回采作业中顶板引起的力学破坏特征是控制采场稳定性的基础。

近年来，国内外专家学者，对此作了大量的研究和总结：靳钟铭[1]，石平五[2]，贾喜荣[3]等分别针对不同地质条件，提出了相应的“悬梁结构”和“薄板矿压理论”力学模型；方新秋等[4-6]基于浅埋煤层近距离工作面开采覆岩运动规律及控制技术进行了系统研究；屠洪盛等[7-10]通过理论分析、实验室模拟及现场调研等手段，针对大倾角厚煤层放顶煤开采矿压显现及覆岩运动规律进行了研究；肖家平等[11-12]通过采用数值模拟软件模拟了上覆岩层岩层运动特征并对工作面应力分布状态进行了分析研究；陈勇等[13-17]基于理论分析和实验室模拟，建立了沿空留巷关键块结构稳定力学模型，理论计算了煤柱宽度与基本顶断裂线位置的关系；姜福兴[18]基于厚板理论，分析求解出不同边界条件下厚板的厚化系数表达式；张益东等[19-23]基于薄板原理，分析探究了在均布载荷作用下工作面顶板的破断机理，并通过相似模拟和理论计算等手段研究了初次来压与周期来压阶段顶板变形规律。

上述关于顶板力学分析研究，多基于均布荷载作用，而在实际生产作业时，基本顶弹性悬板所承受并非均布载荷，而是支承压力载荷[24]，本文基于此建立基本顶弹性力学模型，对支承压力影响下顶板破坏机理进行研究。

1 孤岛工作面顶板力学模型分析

孤岛工作面由于处于两面采空的特殊围岩结构下，随着采空区上覆岩层逐渐稳定，上部岩层重量将向采空区周围新的支承点转移，致使采场周边实体煤或工作面侧承受附加上覆岩层的重量，在采空区两侧煤体出现高于原岩应力的支承压力区(KγH)，孤岛工作面承受相邻2个采空区支承压力叠加影响，围岩应力分布如图1所示。当孤岛工作面进行回采时，孤岛工作面布置图如图2所示。

图1 煤柱顶板应力分布三维示意Fig.1 Three-dimensional stress distribution of coal pillar roof

图2 孤岛工作面布置Fig.2 Arrangement of isolated island working face

孤岛工作面上覆岩层破断规律是影响工作面顶板破坏的主要因素之一，在孤岛工作面回采过程中，由于直接顶岩性较弱，随着工作面的推进，不断垮落，起到了充填采空区的作用；直接顶上方的基本顶岩性较为坚硬，是影响工作面矿压显现的主要因素，如图3～4所示。因此，本文应用理论分析结合数值模拟的手段对基本顶的破坏机理进行研究。

图3 孤岛工作面顶板破裂规律Fig.3 Laws of roof fracture in isolated island working face

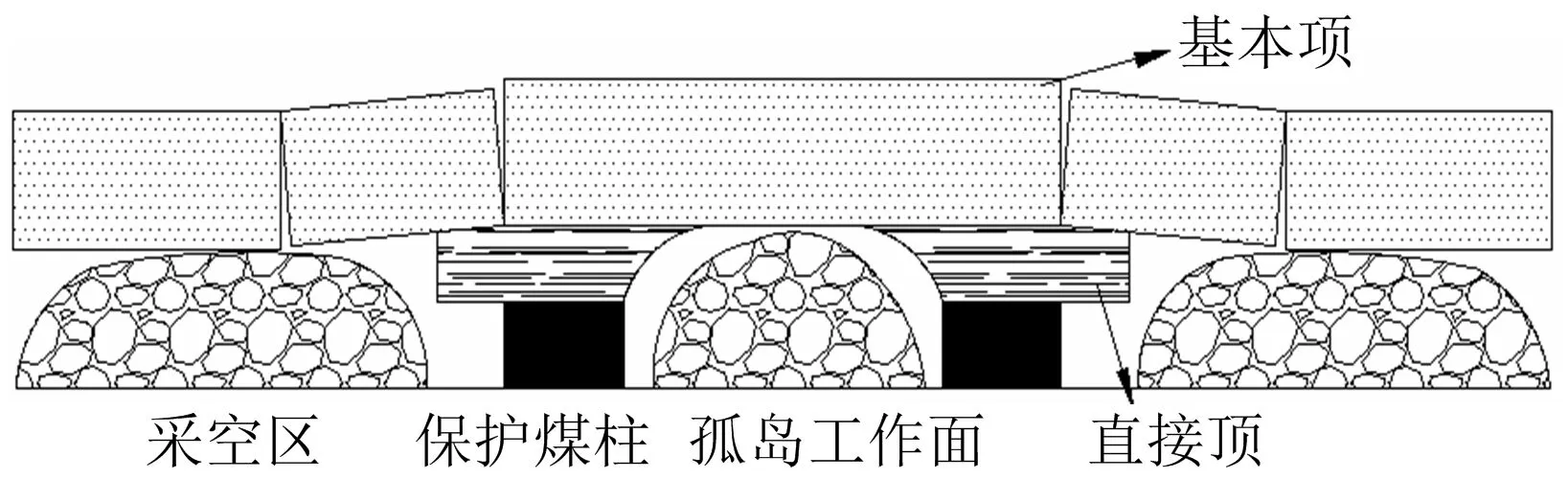
图4 孤岛工作面基本顶未破裂前剖面Fig.4 Profile before fracture of basic roof in isolated island working face

现选取开滦集团东欢坨矿8#煤层中孤岛煤柱所形成的工作面作为案例进行分析，东欢坨矿8#煤层孤岛工作面位于-430水平中央采区，上方无采掘工程，在其下方有-470水平运输大巷，孤岛工作面位置关系如图5所示。8#孤岛煤柱工作面煤厚3.6～4.2 m，平均4 m，煤层倾角3°～6°，平均4°。煤层抗压强度3.18～3.36 MPa。煤岩层性质如图6所示。

图5 孤岛工作面位置关系Fig.5 Position relationship of isolated island working face

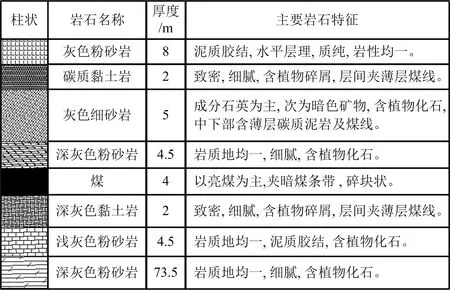
图6 岩性柱状图Fig.6 Lithologic histogram

将孤岛工作面两侧采空及工作面回采后的基本顶视为薄板，基本顶的弹性薄板力学模型边界条件决定着其上方弯矩分布及其断裂步距，同时也是确定工作面支护阻力的重要参数之一。本文通过采用弹性薄板理论，并结合功的互等理论，对孤岛工作面基本顶所受弯矩大小进行研究分析，进而探讨支承压力影响下顶板的破坏机理。弹性薄板的基本系统如图7所示。

图7 弯曲矩形板的基本系统Fig.7 Basic system of curved rectangular plate

薄板边界的支撑条件由孤岛工作面煤柱尺寸大小确定，当煤柱尺寸较小时，煤柱完全处于塑形破坏状态，其不能限制顶板的转动，则该边界视为简支边界；当煤柱尺寸较大时，由于在煤柱中央形成弹性区，煤柱与顶板的夹持作用可限制直接顶转动，则该边界视为固支边界；因而，固支边界满足挠度ω=0，转角∂ω/∂x=0；简支边界满足ω=0，My=0；自由边界满足ω≠0，My=0。在此，只研究当煤柱尺寸为5 m时，孤岛工作面基本顶的破坏机理。

当孤岛工作面煤柱尺寸为5 m时，薄板四周边界条件可以视为对边固支、对边简支的支撑条件，受支承应力影响孤岛工作面基本顶力学模型如图8所示。

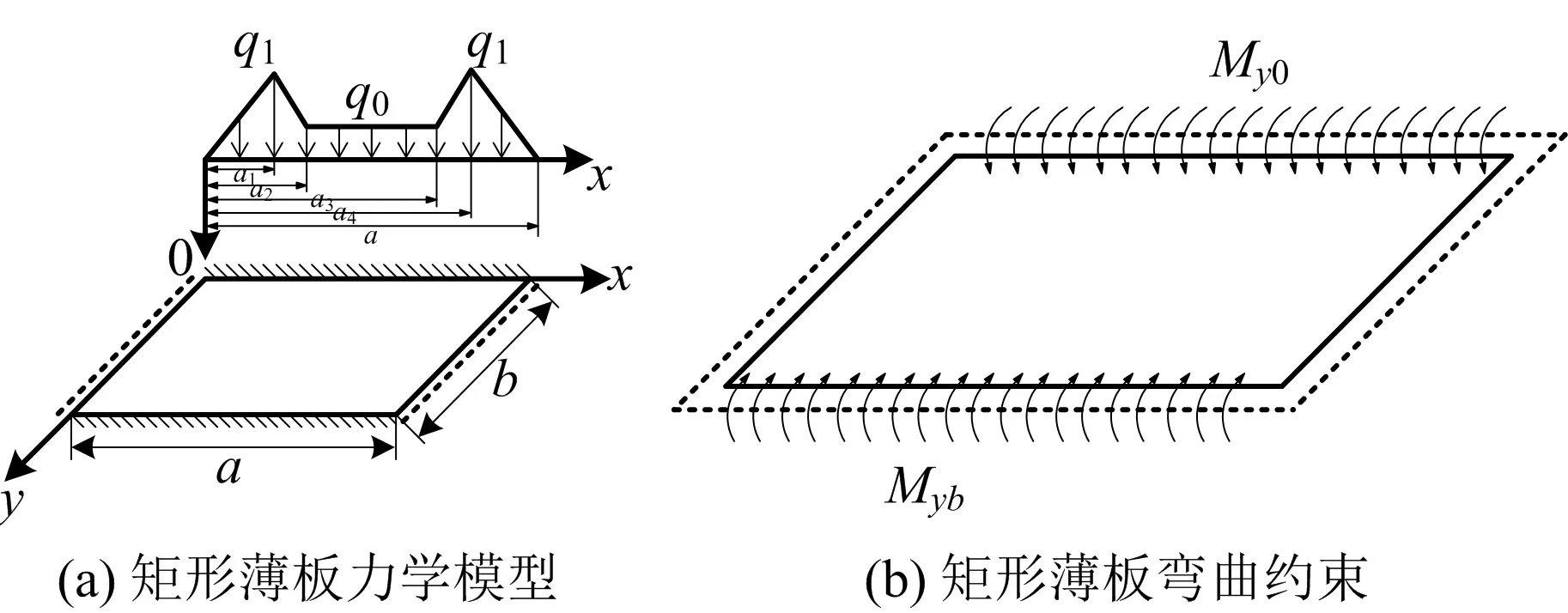
图8 支承压力作用下对边固支、对边简支矩形板Fig.8 Rectangular plates of fixed support and simple support with opposite edges under abutment pressure

对该力学模型进行分析，并将方程进行求解，得到煤壁上方基本顶弯矩表达式为：

Mx=Mx0a1+Mxa1a2+Mxa2a3+Mxa3a4+Mxa4a

(1)

图9为布设于孤岛工作面煤层侧向的检测点监测到的数据，绘制成距孤岛工作面不同距离时，支承压力集中系数的分布规律曲线。由图9可知，支承应力影响范围中：a1=10 m，a2=15 m，q1=3q0，将上述参数带入公式(1)，并对式(1)求解，可得对边固支、对边简支条件，受支承压力影响下，煤壁上方基本顶弯矩；将所得结果进行分析整理，结果如表1所示。

图9 孤岛工作面侧向支承压力集中系数分布Fig.9 Distribution of concentration coefficient for lateral support pressure in isolated island working face

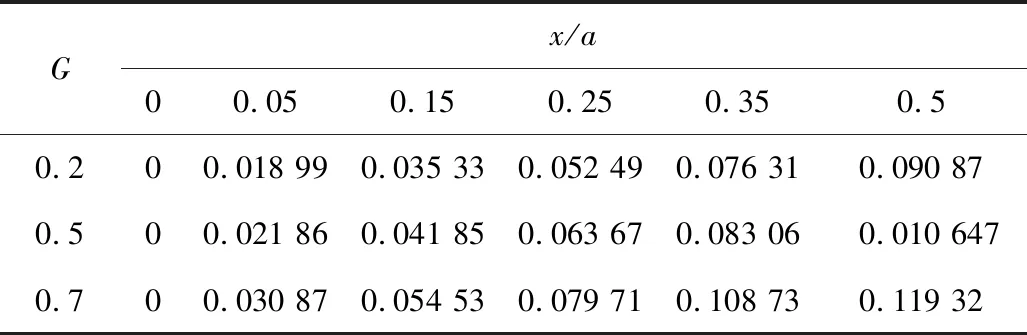
Gx/a00.050.150.250.350.50.200.018 990.035 330.052 490.076 310.090 870.500.021 860.041 850.063 670.083 060.010 6470.700.030 870.054 530.079 710.108 730.119 32

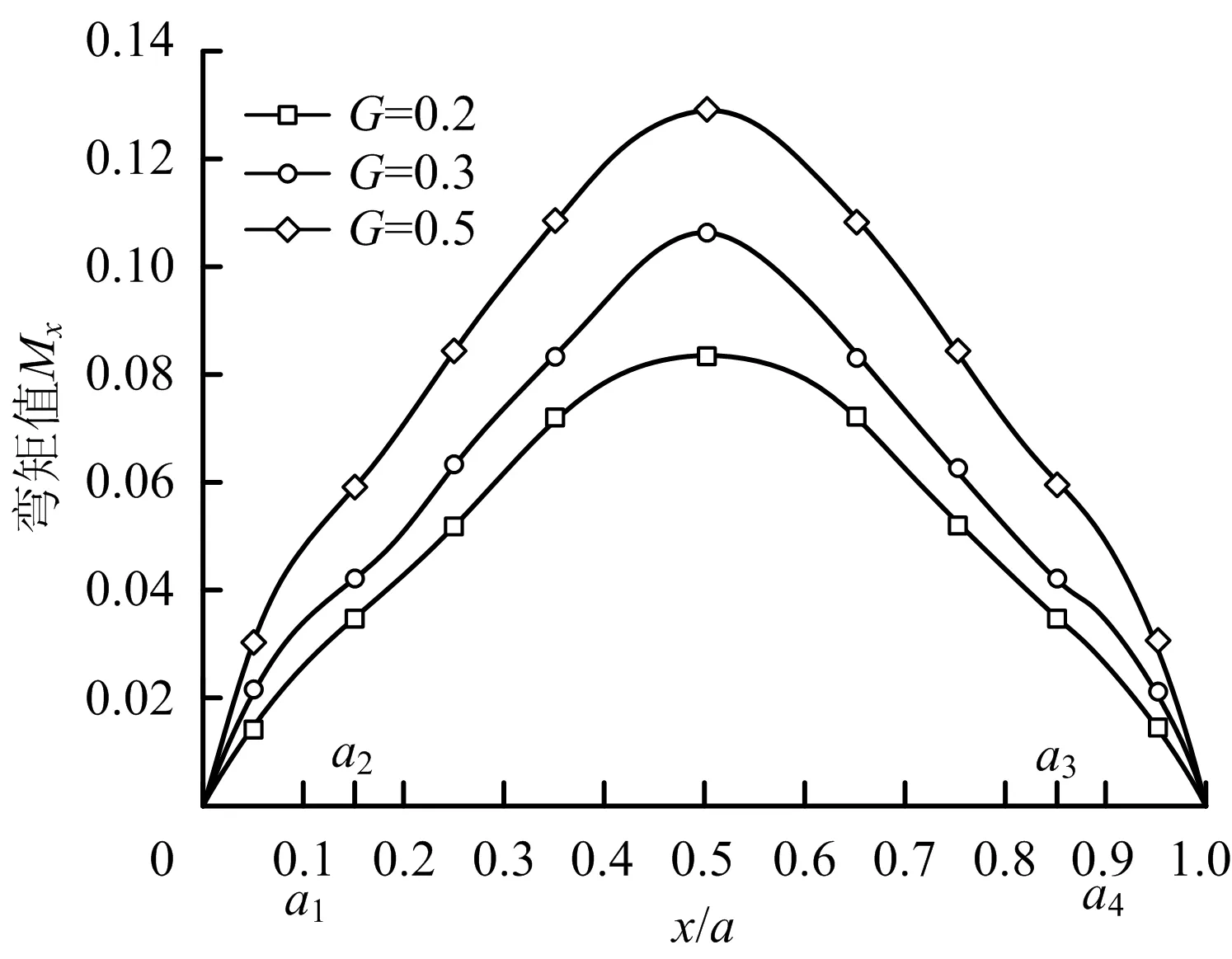
图10 煤壁上方弯矩分布Fig.10 Distribution of bending moment on upper coal wall

煤壁上方弯矩分布如图10所示，在支承压力作用下，煤壁上方基本顶弯矩呈现先增大后减小的趋势，工作面煤壁中部弯矩显著大于煤壁两侧弯矩。该现象合理地解释了工作面方向上支架工作阻力不相等的规律，即工作面中部的支架工作阻力较大，而工作两个端部的支架工作阻力较小。同时可以发现，在支承压力作用下，随着G=b/a(宽长比)的增大(即：工作面长度一定时，工作面推进距离不断增大)，煤壁上方基本顶弯矩呈现增大的趋势，即：在基本顶断裂前，随着工作面向前推进，工作面顶板悬露面积越大，煤壁上方基本顶弯矩越大，顶板覆岩越不稳定。

2 孤岛工作面顶板破坏机理数值模拟研究

结合理论分析所得孤岛工作面顶板弯矩分布的规律，运用三维数值模拟软件FLAC3D，对采场顶板的破坏过程进行模拟，分析在不同推进距离影响下，顶板应力分布及其破坏特征；在顶板悬露面积增大的情况下，沿工作面推进方向上围岩压力的运动变化以及顶板的破坏规律进行总结，从而进一步探讨顶板的破坏机理；对于采场顶板来讲，该假想弥补了沿工作面方向上采场顶板的运动规律这块空白，从而为进一步研究和预测工作面推进方向上围岩压力及顶板破坏规律提供了基础。模型的几何尺寸为560 m×60 m×123.5 m，如图11所示；岩性参数如表2所示。

图11 FLAC3D数值模拟模型及初始应力平衡Fig.11 FLAC3D Numerical simulation model and initial stress balance

表2 岩层岩性力学参数Table 2 Lithologic mechanics parameters of rock stratum

2.1 不同推进距离影响下支承压力的变化

图12为相邻左右工作面已经采空、孤岛工作面正在开采的回采空间周围三维垂直应力分布。如图12所示，在回采空间周围的应力分布十分复杂。在应力集中系数K等于1的范围内，为未受回采影响的原岩应力区；在大于1的范围内，为回采引起的支承压力影响区；应力集中系数可低于1，也可高达2～2.5，在开采深度和围岩性质一定的条件下，围岩应力的变化主要取决于采动状况和煤柱尺寸等因素。如图12(a)所示，当工作面推进距离为5 m时，工作面前方的应力集中系数较小，应力集中系数K1最大为1.1；工作面巷道两侧应力集中系数较大，应力集中系数K2最大为2.6。如图12(b)所示，当工作面推进距离为10 m时，工作面前方的应力集中系数较小，应力集中系数K1最大为1.26；工作面巷道两侧应力集中系数较大，应力集中系数K2最大为2.7。如图12(c)所示，当工作面推进距离为15 m时，工作面前方的应力集中系数较小，应力集中系数K1最大为1.37；工作面巷道两侧应力集中系数较大，应力集中系数K2最大为2.8。如图12(d)所示，当工作面推进距离为25 m时，工作面前方的应力集中系数较小，应力集中系数K1最大为1.51；工作面巷道两侧应力集中系数较大，应力集中系数K2最大为3.1。

图12 回采空间周围三维垂直应力分布Fig.12 Three-dimensional vertical stress distribution around mining space

综合不同推进距离时工作面前方应力集中系数K1和工作面巷道两侧应力集中系数K2的影响研究结果，汇总至表3，并绘制图13。

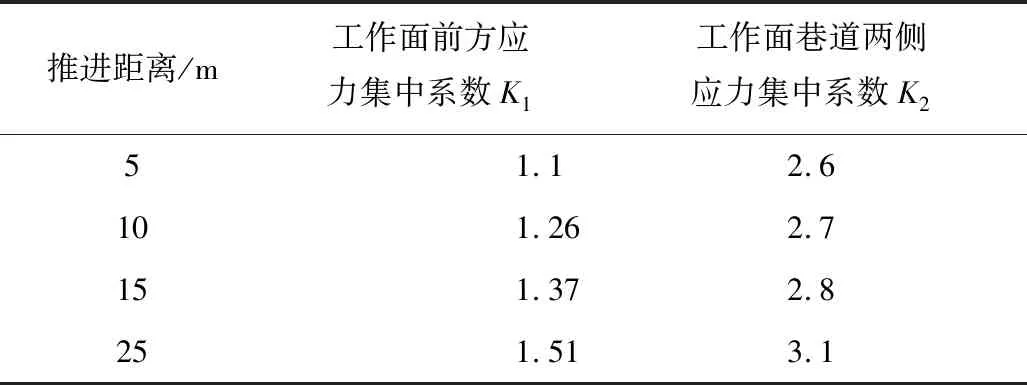
表3 不同推进距离对K1，K2的影响情况Table 3 Influence of different advancing distances on K1 and K2

图13 不同推进距离时应力集中系数分布Fig.13 Distribution of stress concentration coefficient under different advancing distances

如图13所示，随着工作面推进距离的不断增大，工作面前方应力集中系数K1和工作面两侧巷道应力集中系数K2呈现线性增大的趋势。工作面前方应力集中系数K1受推进距离影响不大，但巷道两侧应力集中系数K2受推进距离的影响较大。由图13可得，当推进距离为5 m时，此时工作面前方应力集中系数K1和巷道两侧应力集中系数K2最小，对工作面和巷道维护最为有利。

2.2 不同推进距离对顶板稳定性的影响

如图14(a)所示，当工作面推进距离为5 m时，工作面顶板应力值为2.0 MPa；如图14(b)所示，当工作面推进距离为10 m时，顶板应力值为4.0 MPa；如图14(c)所示，当工作面推进为15 m时，顶板应力值为4.72 MPa；如图14(d)所示，当工作面推进距离为25 m时，顶板应力值为5.0 MPa。将以上数据进行整理汇总至表4，并绘制图15。

图14 顶板应力云图Fig.14 Roof stress cloud diagram

推进距离/m顶板应力值/MPa52.0104.0154.72255.0

图15 不同推进距离时，顶板应力值Fig.15 Stress values of roof under different advancing distances

如图15所示，通过模拟煤层顶板应力场的演变过程，可以发现，随着工作面的不断推进，顶板靠近工作面煤壁侧的应力值呈现逐渐增大的趋势，并随着推进距离的不断增大，应力集中现象随之扩散。

此外，为了更好地对孤岛工作面顶板破坏机理研究提供有力的理论依据，通过在孤岛工作面开切眼前方50 m处布置1#监测点，(监测点布置方案如图16所示)，对孤岛工作面开采过程中的顶板位移与能量值等参数进行记录和整理，监测结果如图17所示。

图16 孤岛工作面监测点布置方案Fig.16 Layout plan of monitoring points in isolated island working face

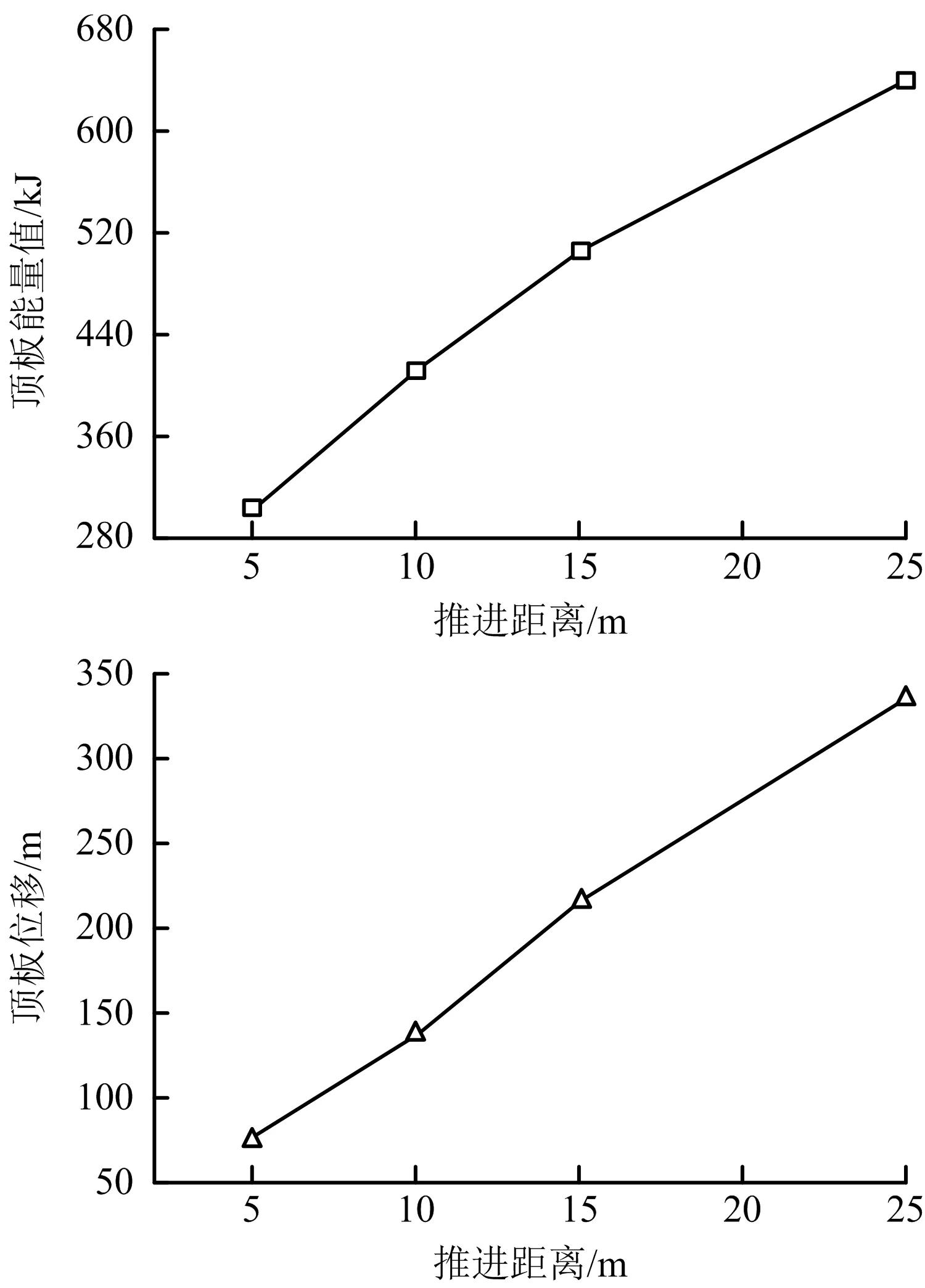
图17 不同推进距离时，顶板位移与能量值Fig.17 Roof displacement and energy values under different advancing distance

从图17可以看出，顶板位移及顶板能量值与孤岛工作面推进距离呈现正相关趋势，即：随着工作面的不断推进，顶板下沉量逐渐增大；同时，顶板积聚的能量也越来越多，顶板越来越不稳定，为后续顶板破断规律的研究提供一定的数值依据。

顶板塑性区破坏过程如图18所示。

图18 顶板塑性区破坏Fig.18 Failure of plastic zone in roof

从图18(a)可以看出，当工作面推进5 m时，顶板在工作面长边处首先发生拉伸破坏，在短边处发生剪切破坏,由岩石的强度特征可知，σ拉<σ剪<σ压，故顶板在拉伸破坏严重的地方最先破断，因此沿工作面煤壁(即薄板长边)拉应力最大处薄板开始破断；如图18(b)所示，随着工作面的不断向前推进，当工作面的推进距离为10 m时，顶板悬露面积进一步增大，顶板工作面长边拉伸破坏范围进一步增大，并在短边处剪切破坏范围进一步增大，同时出现拉伸破坏；如图18(c)所示，随着工作面的不断推进，当推进距离增大到15 m时，顶板长边处与短边处的拉伸破坏范围进一步增大，顶板悬露面积越来越大，顶板越来越不稳定；如图18(d)所示，随着工作面的不断推进，当推进距离为25 m时，顶板悬露面积进一步增大，顶板长边和短边拉伸破坏范围进一步扩大，四周相互贯通，形成“O”形破坏；顶板端角处的剪切破坏进一步增大，相互贯通，形成空间的横“X”型破断。

如塑性区破坏过程所示，孤岛工作面顶板的破断规律与推进距离有着密切的联系，表现为覆岩破坏的时空效应。通过对不同推进距离时顶板塑性区破坏进行分析发现顶板断裂的塑性区演变的时空效应及力学特征。孤岛工作面顶板破断随着工作面的推进呈现以下几个状态：①采动初期，顶板首先在长边中点发生破断，并逐渐向两端扩散；②随着工作面的继续推进，顶板短边中点开始发生破断，并逐渐与长边端部破断相互贯通，构成环形破断，形成平面的横向“O”型破坏；③随着工作面继续向前推进，工作面顶板中心处发生破断，产生与工作面相互平行的裂纹，裂纹并不断向短边端部扩散，最后与长边端部和短边端部形成横向“X”型破断；④顶板四周所形成的横向“O”型破断和横向“X”型破断，共同构成了顶板破断的横“O-X”破断形式。顶板破断的演化过程如图19所示。

图19 采场顶板横“O-X”型破断演化过程Fig.19 Evolution process of transverse “O-X” fracture in mining roof

3 结论

1)通过建立薄板力学模型分析发现：在支承压力作用下，沿工作面倾向，煤壁上方基本顶弯矩呈现先增大后减小的趋势，工作面煤壁中部弯矩显著大于煤壁两侧弯矩；随着工作面推进距离的增大，顶板弯矩呈现增大的趋势，研究所得结论为后文数值模拟实验顶板破坏分析提供了理论依据。

2)通过分析孤岛工作面在不同推进距离时，顶板应力集中系数的变化规律发现：随着推进距离的不断增大，工作面前方应力集中系数K1和工作面两侧巷道应力集中系数K2，呈现线性增大的趋势。

3)通过分析不同推进距离，顶板应力、位移与能力值的变化规律发现：随着工作面推进距离的不断增大，孤岛工作面顶板越来越不稳定，为后续顶板破断规律的研究提供一定的数值依据。

4)通过对不同推进距离时，顶板塑性区破坏进行分析发现：顶板断裂的塑性区演变特征存在时空效应及力学特征，顶板四周所形成的横向“O”型破断和横向“X”型破断，共同构成了顶板破断的横“O-X”破断形式。