弹载数据链在不同作战模式下的效能研究

赵 日，许泽宇，孔繁良，赵鹏飞

(中国运载火箭技术研究院， 北京 100076)

随着智能化协同反舰作战概念的逐渐成熟，弹载数据链技术得到了长足的发展。基于弹载数据链进行信息共享和协同作战已经成为反舰导弹的主要发展方向[1]。在协同反舰作战时，由于弹载数据链的存在，不同波次之间、同一波次不同导弹之间均可以进行信息共享，结合反舰导弹雷达导引头探测能力，即可实现基于前一波次探测信息校正后一波次射击的观校射击的作战方式。本文即针对不同情况下弹载数据链对反舰作战效能的影响开展研究，可为信息化条件下反舰导弹作战使用提供支撑。

1 打击效果评估模型

自反舰导弹的射程突破视距后，低目指精度条件下对海打击就成为一种常态，针对低目指精度条件下导弹捕捉能力的研究比较多[2-3]，同时针对该条件下反舰导弹射击方式的研究也从未停止[4-7]。文献[8]提出的齐射方式，其核心思想是各枚导弹均瞄准目标散布中心这同一点进行射击，显然此时各枚导弹的搜索域/打击域存在较大重叠，不利于发挥最佳作战效能。而反舰作战中，通常仅需一枚导弹命中目标，即可使舰艇退出战斗序列。故在目标散布范围较大时，如果科学地分开设置各枚导弹的瞄准点，可以形成覆盖范围更大的联合搜索域，则有可能提高反舰导弹齐射的作战效果。本文提出单波次打击和多波次打击效果评估模型，可对不同情况下弹载数据链对打击效果的影响进行定量分析。

为对不同打击模式下的作战效能进行计算，运用概率基本思想，构建分析模型。为便于开展建模分析，可假设目标散布服从二维独立正态分布，在导弹打击域内单发导弹命中概率为p0。下面分析时，建立坐标原点为目标散布中心，X轴为正东方向，Y轴为真北方向的直角坐标系。

在目标散布范围内其位于坐标(x,y)点的概率可由其目标分布概率密度函数fE(x,y)表示：

(1)

假设目标位于(x,y)点时，被至少一发导弹命中的条件概率为PTE(x,y)，则在多发弹射击时，目标被命中的概率可表示为

(2)

式(2)中，积分区间Ω为目标散布范围；PTE(x,y)由所采取的作战样式(单波次打击或多波次打击)和单发命中概率p0确定。下面具体分析两种不同打击模式下目标命中概率的计算方法。

1.1 单波次打击

1.1.1“搜索范围=打击范围”的情况

此种情况表示，弹上雷达导引头搜索范围与导弹打击范围一致。假设单发导弹打击范围为以瞄准点为中心半径为RA的圆域，单发导弹搜索范围为以瞄准点为中心半径为RS的圆域，则此时RS=RA；假设第i发导弹的瞄准点为(ai,bi)，则第i发导弹命中目标的概率由目标在该时刻所处位置、导弹打击范围决定以及单发命中概率p0确定，在目标分布服从正态分布的情况下，第i发导弹命中目标概率可表示为

(3)

Q=P1∪P2∪Pi…∪Pn

(4)

则最佳火力打击效果，即是寻求一组瞄准点使得Q值最大，可表示为

maxQ

s.t.(ai,bi)∈Ω

(5)

1.1.2“搜索范围>打击范围”的情况

此种情况表示，弹上雷达导引头搜索范围大于导弹打击范围(主要受导弹机动能力限制)，存在可发现目标但无法实现打击的情况，此时RS>RA。此种情况下的最佳火力打击效果，也是寻求一组瞄准点使得P值最大，求解方式与结果均与2.1.1节完全相同。所不同的是，由于此种情况下导引头搜索范围大于导弹打击范围，此时还需要对目标发现概率进行分析。

在最优瞄准点选定后，求目标发现概率问题可表示为

Pf=Pf1∪Pf2∪Pfi…∪Pfn

(6)

式(6)中，Pfi为第i发导弹发现目标的概率，计算公式如下：

(7)

1.2 多波次打击

此种情况下，打击将分多波次进行。若弹上有数据链，导引头探测信息可通过弹载数据链回传后端指挥中心，各波次间可进行协同作战分配；若弹上无数据链，导引头探测信息无法回传指挥中心，各打击波次间作战分配相互独立。

1.2.1“搜索范围=打击范围”的情况

第i发导弹命中目标的概率表达式同式(3)。第j波次n发齐射情况下，导弹命中目标的概率可表示为

Qj=P1∪P2∪Pi…∪Pn

(8)

则m波次打击中，导弹命中目标的概率为

Q=Q1∪Q2∪Qj…∪Qm

(9)

此时，最佳火力打击效果即可转换为求解m组瞄准点，使得式(9)取最大值，也即

maxQ

s.t.(ai,bi)j∈Ω，j=1,2,3，…，m

(10)

针对上述问题的求解，需要根据有无弹载数据链分成两种情况。

若无弹载数据链，则后一波次不知道前一波次打击效果，于是每一波次打击均是在无先验信息的情况下追求该波次打击效果最优。若每一波次发射导弹数量相同，则各波次攻击命中目标概率相同，即Q=P1=P2=Pj=…=Pm。

若有弹载数据链，则后一波次将得知前一波次的命中情况，于是就可以相应的调整当前波次的打击方案，且只有当前一波次未命中目标时才会进行当前波次的射击，同时每一波次的射击也均是要追求本波次射击效果最优，随着射击波次的增加，对目标的命中概率也将逐渐增加。

1.2.2“搜索范围>打击范围”的情况

此时，存在导弹可以发现目标但由于机动能力有限而无法命中目标的情况。

若弹上无数据链，则多波次打击最佳火力分配任务与2.2.1节相同，差异仅在于还需对目标发现概率进行分析。也即分析在最优打击瞄准点情况下，导弹对目标的发现概率。

Pf=Pf1∪Pf2∪Pfi…∪Pfm

(11)

其中，Pfm为第m波次打击时对目标的发现概率，计算方法与2.1.2节相同。

若弹上有数据链，第一波次命中概率、发现概率求解方式与2.1.2节完全相同；在进行第二波次打击时，需要分3种情况进行考虑：

目标被命中：此时无需再进行第二波次打击。

目标被发现但未被命中：此时目标具体位置已知，此时将发动第二波次导弹对目标进行打击。

目标未被发现也未被命中：此时第二波次打击命中概率求解可表示为

(12)

Q=P1∪P2∪Pi…∪Pn

(13)

则此波次火力打击效果，即是寻求一组瞄准点使得Q值最大，可表示为

maxQ

s.t.(ai,bi)∈Ω2

(14)

其中，Ω2为第一波次发现区域外目标可能存在的区域。综上，两波次打击情况下，对目标的命中概率可表示为

QΣ=P1+P21+P22

(15)

其中，P1为第一波命中概率，P21为第一波次目标被发现但未被命中情况下被第二波次命中的概率，P22为第一波次目标未被发现也未被命中情况下被第二波次命中的概率。

2 仿真分析

假设目标位置服从σx=σy=25 km、μx=μy=0的二维正态分布，导弹打击半径RA为30 km，导弹搜索半径RS为40 km，导弹单发命中概率p0取为0.8。针对有无弹载数据链情况下进行两波次射击时反舰导弹对目标的命中概率进行仿真计算。

弹上无数据链时的仿真结果见表1和表2，由表1和表2可见：在发射相同数量导弹时，采用先后波次攻击的效果没有同波次齐射攻击好。例如，同样发射3枚导弹时采用同波次齐射命中概率为0.665 1，而采用先后波次打击时的命中概率为0.566 8。同样，对于目标发现概率也有相同结论。

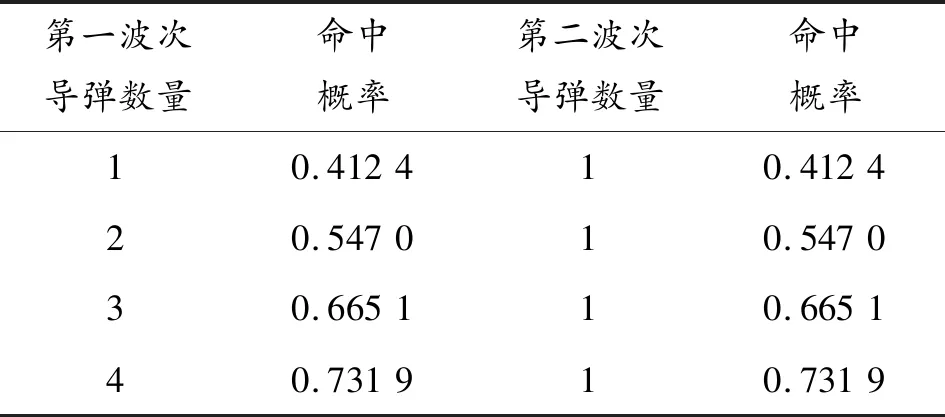
表1 无弹载数据链(RS=RA)

表2 无弹载数据链(RS>RA)

以同时发射3发导弹为例，无弹载数据链时，同一波次齐射和先后波次射击情况下，导弹打击范围仿真结果见图1和图2。由图1和图2可见，由于第二波次不知道前一波次的打击情况，其将会以目标散布中心为瞄准点，结果将导致整体作战效果不佳。图中红圈表示目标散布范围，蓝圈表示单发导弹打击范围，下同。

图1 无弹载数据链同波次发射3发导弹

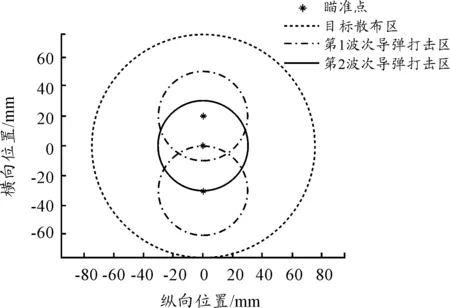
图2 无弹载数据链先后波次发射3发导弹

弹上有数据链时的仿真结果见表3和表4：

1) 导弹探测范围等于打击范围的情况(表3)：在发射相同数量导弹时，虽然作战效果比无弹载数据链时有所提升，但采用先后波次攻击的效果仍没有同波次齐射攻击好。例如，同样发射3枚导弹时采用同波次齐射命中概率为0.665 1，无弹载数据链时采用先后波次打击时的命中概率为0.566 8，有弹载数据链时采用先后波次打击时的命中概率为0.635 0。

表3 有弹载数据链(RS=RA)

以同时发射3发导弹为例，同一波次齐射情况同图1，有弹载数据链时先后波次射击情况见图3。可见，虽然后一波次已知前一波次射击结果，但由于目标在散布中心出现概率最大，此时采用先后波次射击效果仍没有同波次射击好。

图3 有弹载数据链先后波次发射3发导弹

2) 导弹探测范围大于打击范围的情况(表4)：在发射相同数量导弹时，采用先后波次攻击的效果比同波次齐射攻击好。例如，同样发射3枚导弹时采用同波次齐射命中概率为0.665 1，有弹载数据链时采用先后波次打击时的命中概率为0.719 4。

表4 有弹载数据链(RS>RA)

以同时发射3发导弹为例，同一波次齐射打击情况同图1，有弹载数据链时先后波次射击情况见图4。可见，此时由于导弹探测范围大于打击范围，在后一波次打击时存在前一波次发现但受导弹能力限制无法打击的情况，第二波次打击可以弥补第一波次的这种缺陷，从而提升整体作战效能。图4中黑圈表示导弹探测能力范围。

图4 有弹载数据链先后波次发射3发导弹

3 结论

1) 弹上无数据链时，后一攻击波次不知道前一波次打击效果，每一波次均是追求当前波次打击效果最优，在总发射导弹数量相同时，多波次打击没有单波次打击效果好；

2) 弹上有数据链时，若导弹搜索范围与可命中范围大小一致，在总发射导弹数量相同时，多波次攻击的作战效能比无数据链时有所提升，但没有单波次多弹齐射效果好；

3) 弹上有数据链时，若导弹搜索范围大于可命中范围，在总发射导弹数量相同时，多波次攻击可提升作战效能。