高原条件下无控旋转弹丸弹道建模与仿真研究

2019-07-04刘玉文张志远

兵器装备工程学报 2019年5期

刘玉文,蒋明,李泳,张志远

(陆军炮兵防空兵学院兵器工程系火控技术教研室，合肥 230031)

1 高原条件下刚体弹道模型的建立

结合经典弹道理论和方法，按照“先建立坐标系，再分析受力和力矩，而后根据牛顿力学的动量定理和动量矩定理建立运动参数与受力之间关系并分解到坐标系各坐标轴上”的思路，建立高原条件下的刚体弹道模型。限于篇幅，省去过程，直接给出高原条件下无控旋转弹丸的刚体弹道方程组。

sinδ2=cosψ2sinφ2-sinψ2cosφ2cos(φa-θa)

sinδ1=cosφ2sin(φa-θa)/cosδ2

sinβ1=sinψ2sin(φa-θa)/cosδ2

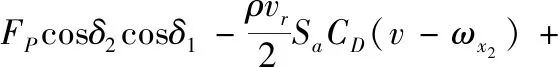
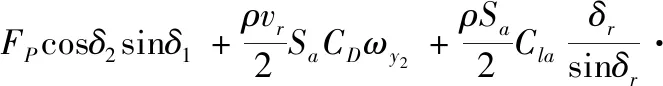
[(v-ωx2)sinδ2+ωz2cosδ2cosδ1)]-

2ΩEmv(sinψ2cosθacosΛcosαN+sinθasinψ2sinΛ+

cosψ2cosΛsinαN)

2ΩEmv(sinΛcosθa-cosΛsinθacosαN)

vrξ=(v-ωx2)cosδ2cosδ1-ωy2cosδ2sinδ1-ωz2sinδ2

vrη=vrη2cosβ+vrζ2sinβ,vrζ=-vrη2sinβ+vrζ2cosβ

vrη2=-(v-ωx2)sinδ1-ωy2cosδ1

vrζ2= -(v-ωx2)sinδ2cosδ1+ωy2sinδ2sinδ1-ωz2cosδ2

ωx2=ωxcosψ2cosθa+wzsinψ2

ωy2=-ωxsinθa

ωz2=-ωxsinψ2cosθa+wzcosψ2

ωx=-ωcos(αW-αN)

wz=-ωsin(αW-αN)

以上即是高原条件下弹丸的六自由度刚体弹道模型，共涉及15个变量：v，θa，ψ2，φa，φ2，δ2，δ1，ωξ，ωη，ωζ，γ，x，y，z，β，也有15个方程。各符号含义同一般外弹道学教材。

2 无控旋转弹丸外弹道仿真及特性分析

无控旋转弹丸高原外弹道特性主要包含弹丸质心运动特性和绕质心运动特性。利用上面弹道方程，结合获取的高原条件下的某型弹丸气动参数，进行仿真计算，根据计算结果分析高原弹道特性的变化特征。仿真时，为了清晰反映高原外弹道特性的变化规律，从海拔0～5 000 m，每隔1 000 m选取一个高程。质心运动特性包括弹道轨迹、速度、速度高低角(弹道倾角)、速度方向角等参数的特性，绕质心运动特性主要包括弹轴高低角、弹轴方向角、攻角、动力平衡角、转速等参数的特性。

2.1 弹道轨迹随高程变化规律

以某火炮榴弹为例，对某一药号，不同射角进行仿真计算。图1～图4是射角30°时，X～Y、X～Z、T～θ、T～V曲线。图5～图8是射角60°时，X～Y、X～Z、T～θ、T～V曲线。

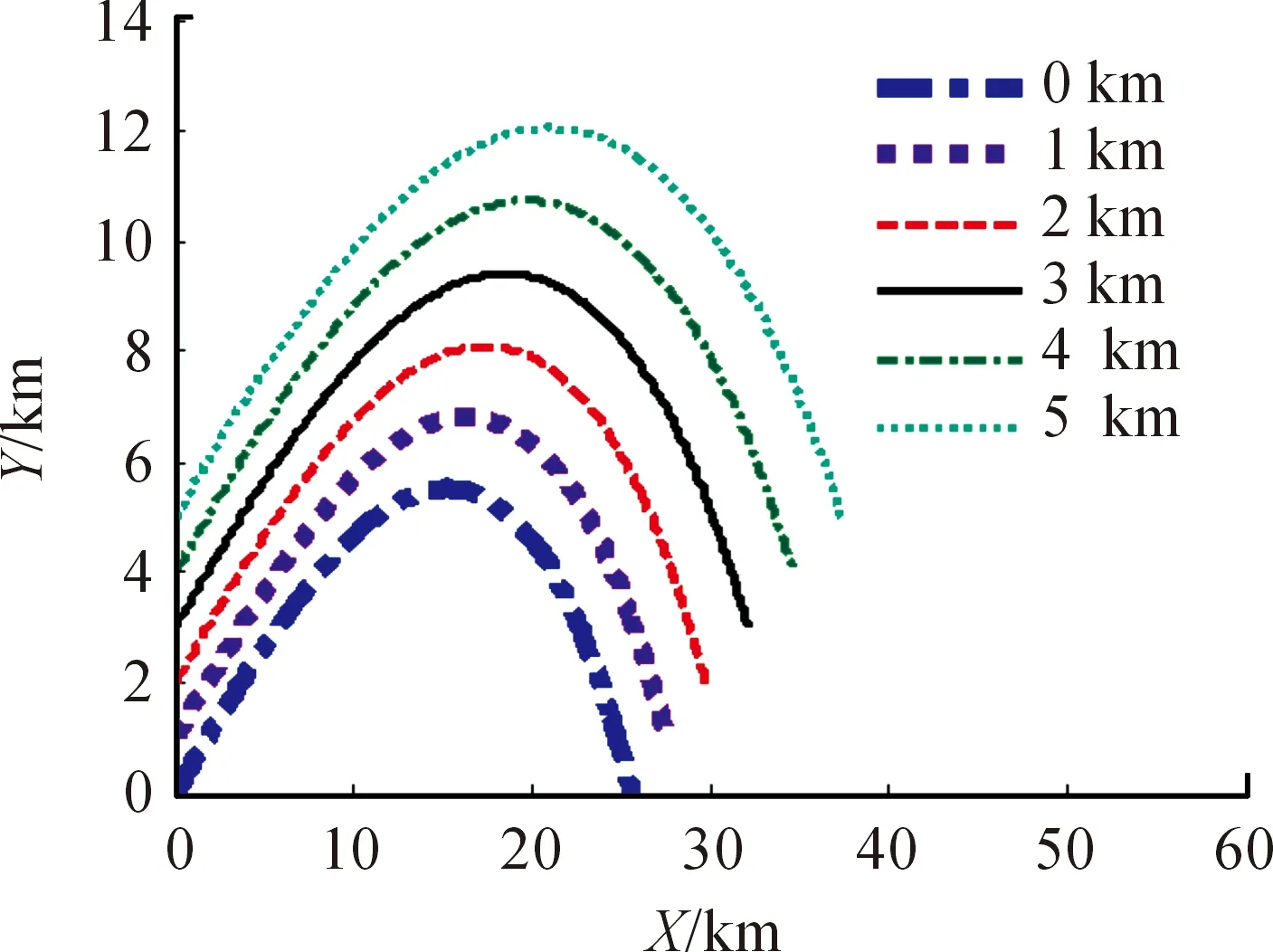
图1 射角30°时X～Y曲线

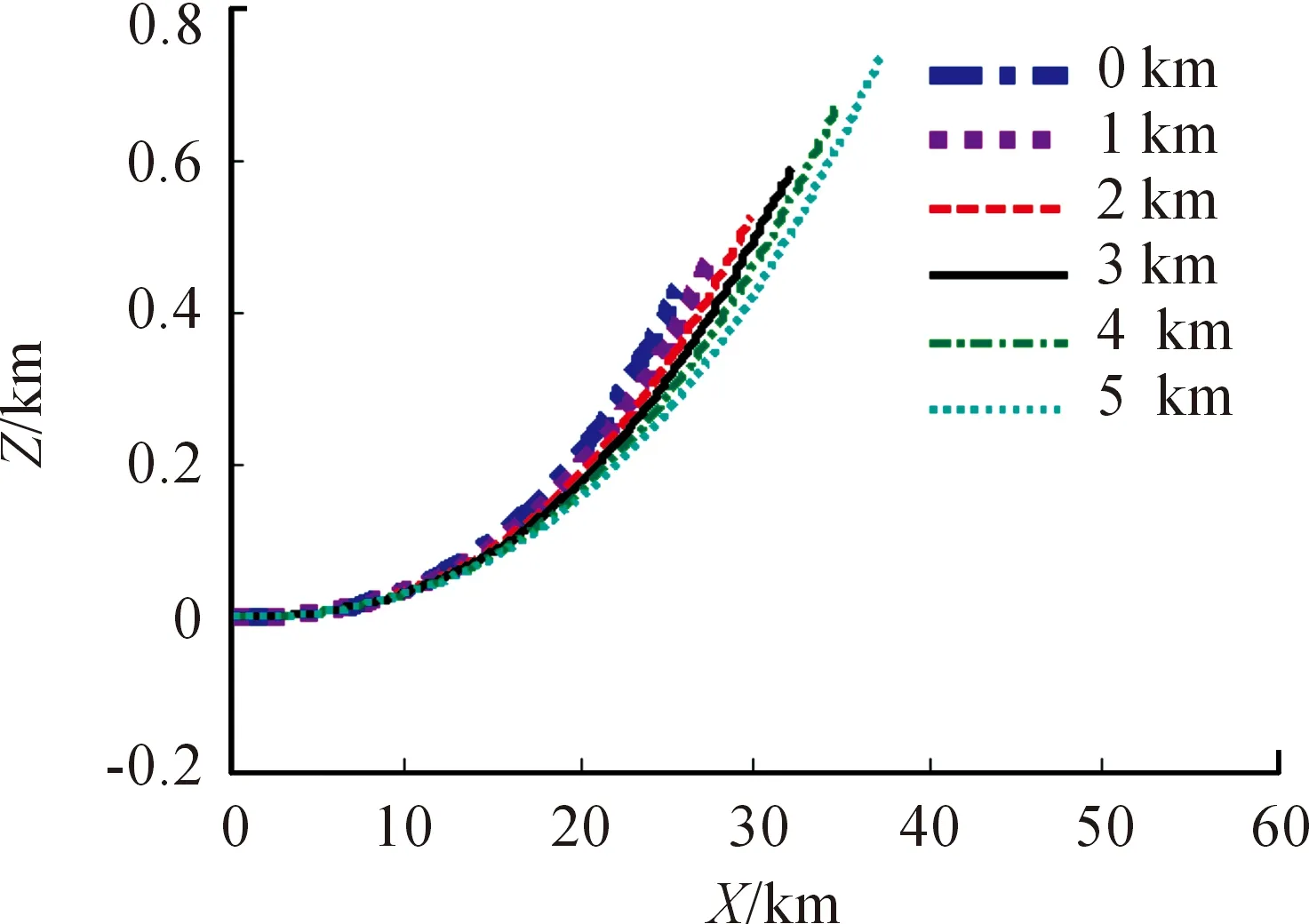
图2 射角30°时X～Z曲线

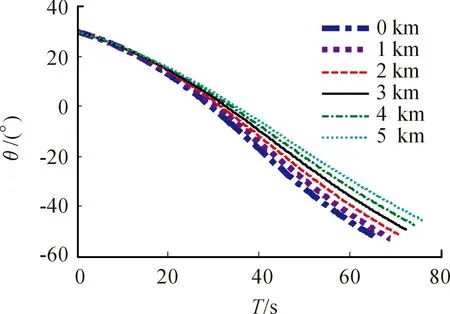
图3 射角30°时T～θ曲线

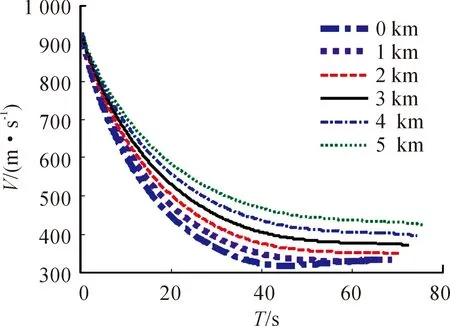
图4 射角30°时T～V曲线

图5 射角60°时X～Y曲线

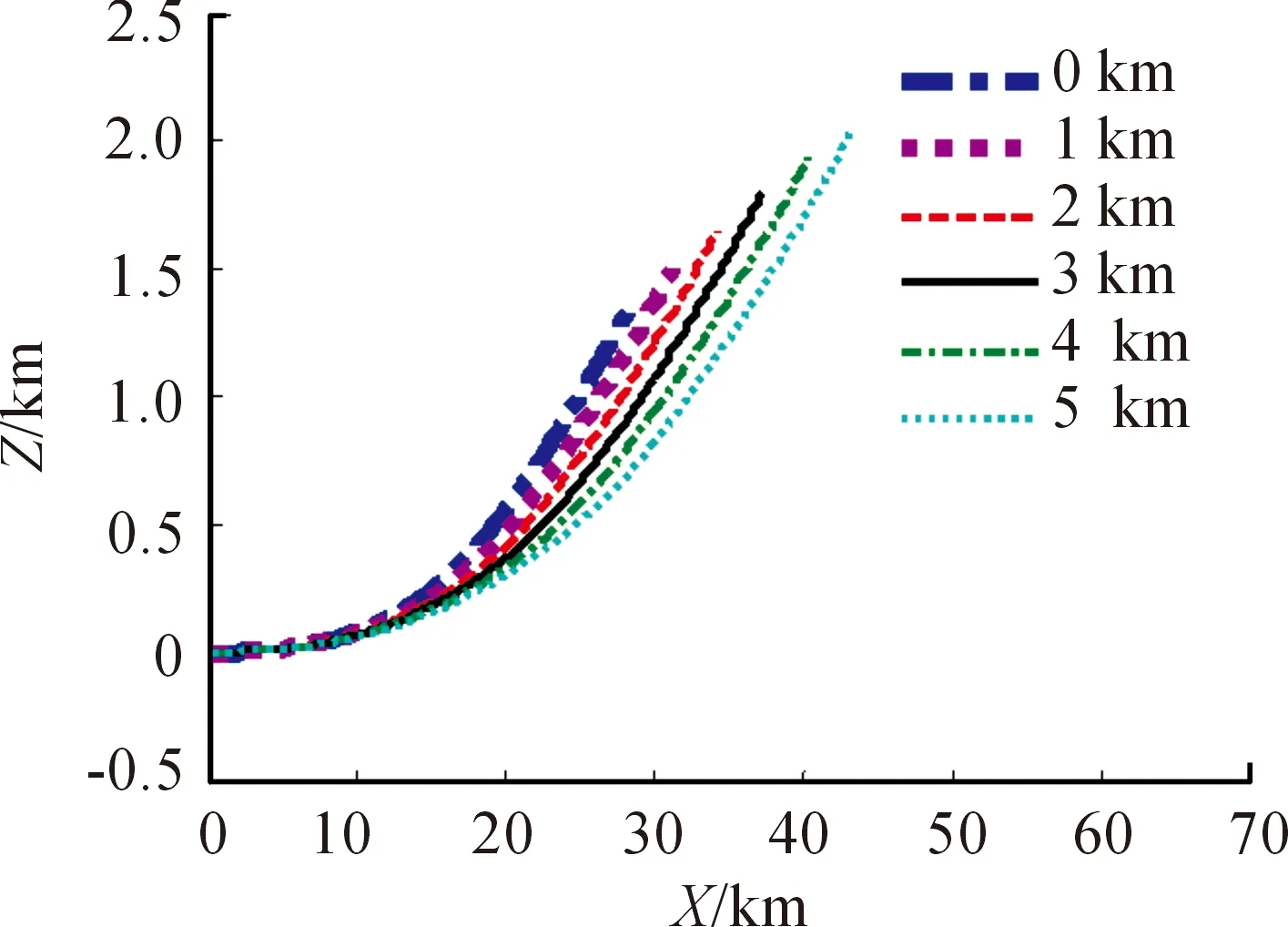
图6 射角60°时X～Z曲线

通过对计算结果的比较可以发现，随着阵地高程的增加，射程和侧偏距离增大。此外，通过弹道倾角的变化规律也可以看出，随着高程的增加，弹道倾角变化速度变得平缓，也即说明弹道轨迹变得平直。

图7 射角60°时T～θ曲线

图8 射角45°时T～V曲线

2.2 高原绕质心运动特性

绕质心运动特性，主要是指弹轴方向的相对地面参考坐标系的变化和弹丸飞行攻角的变化。弹轴方向的相对地面参考坐标系的变化又包括弹轴高低角和方向角的变化，飞行攻角又可分解为高低攻角和方向攻角，两者主要描述弹丸俯仰运动特性。此外弹丸的滚转运动也是绕质心运动的一个方面。

2.2.1弹轴方向随阵地高程变化规律

仍选取射角30°、60°，考察弹轴方位角、弹轴高低角的变化规律随阵地高程变化的情况。如图9～图12所示。

通过对计算结果的分析可知，随着高程的增加，弹轴方位角变大。海拔高度从0～5 000 m，射角30°时，弹轴方位角最大值的变化范围为2.05°～2.48°，射角60°时，弹轴方位角最大值变化范围8.13°～22.03°。

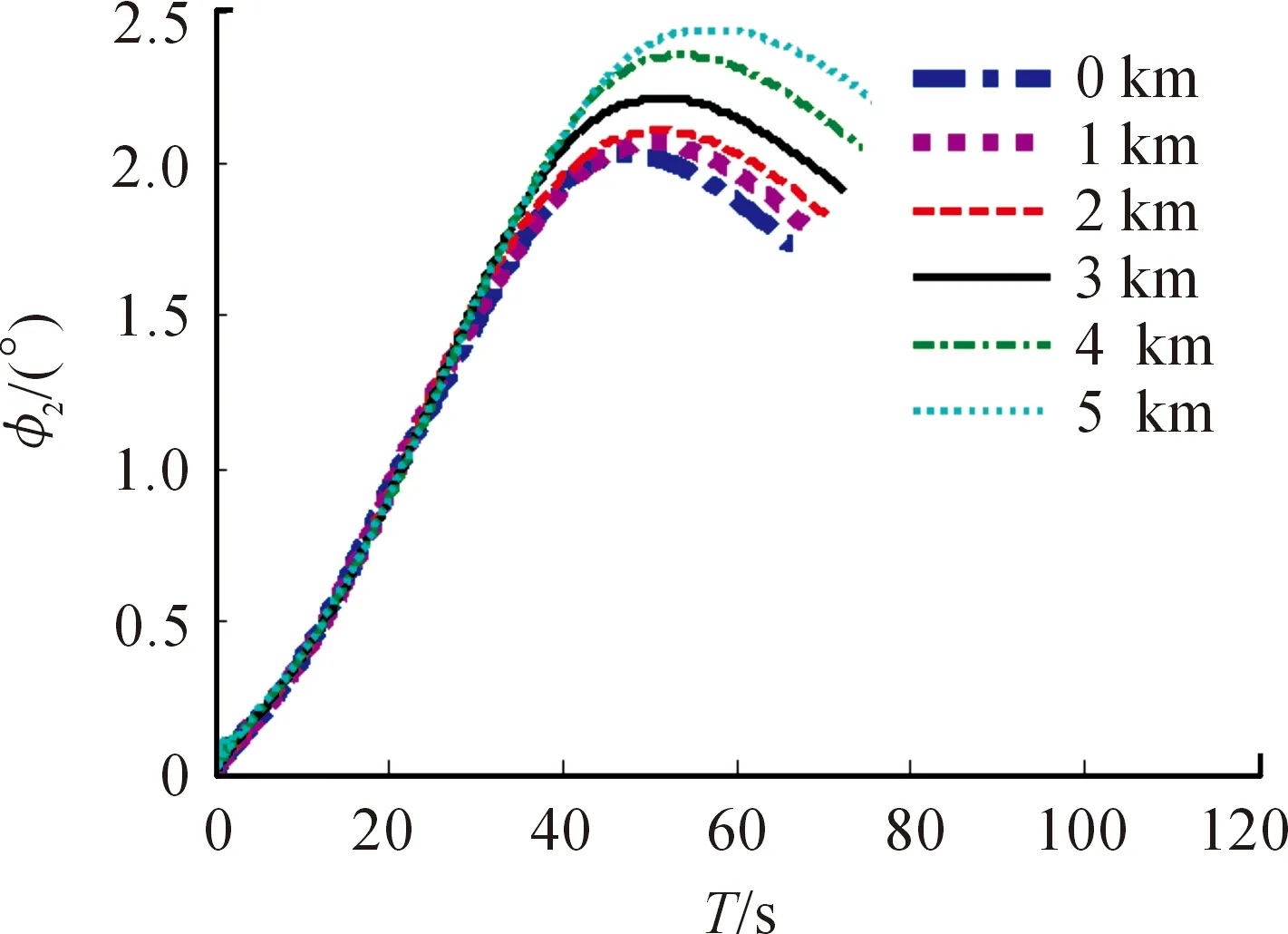
图9 射角30°，弹轴方位角

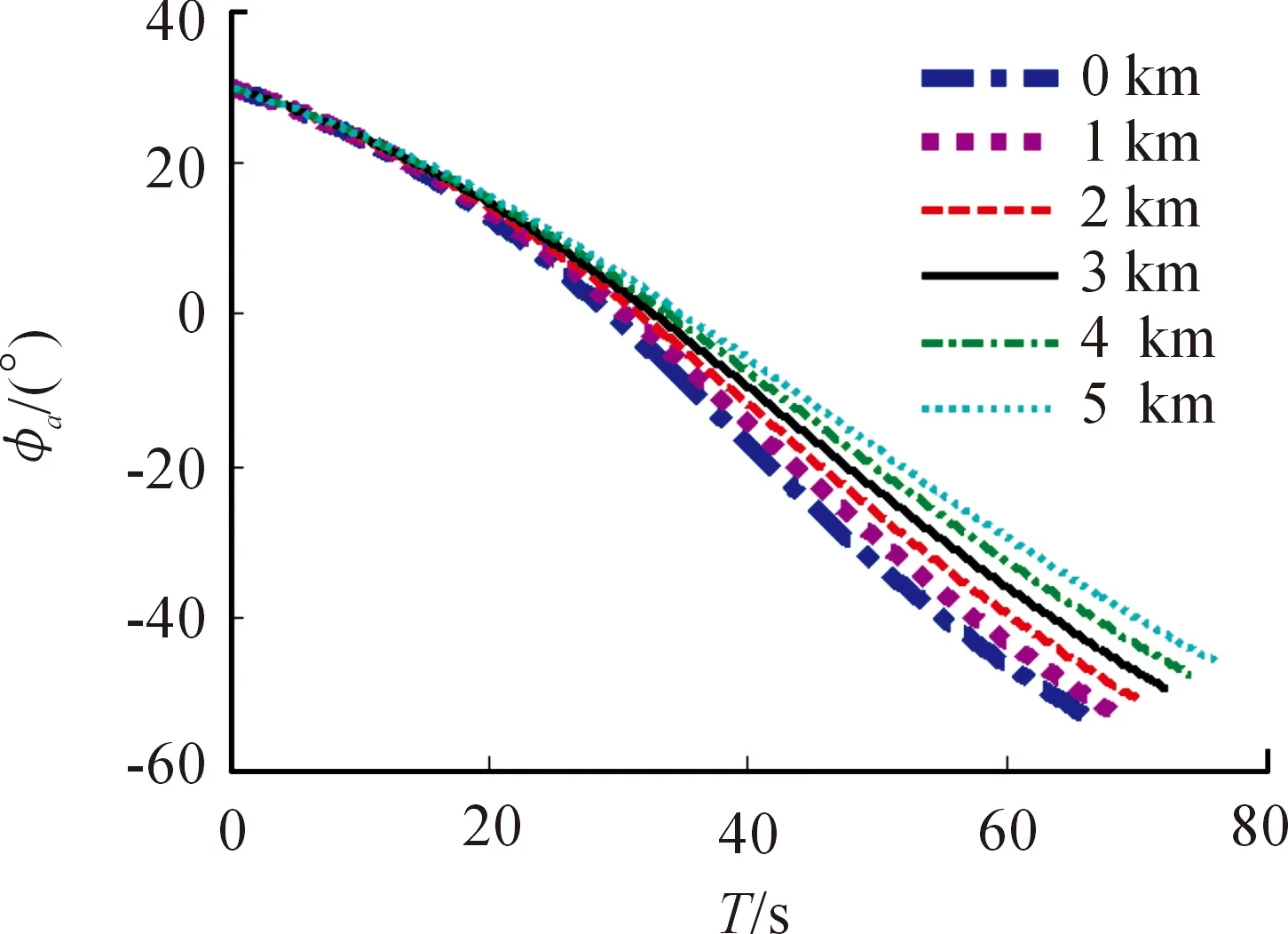
图10 射角30°，弹轴高低角

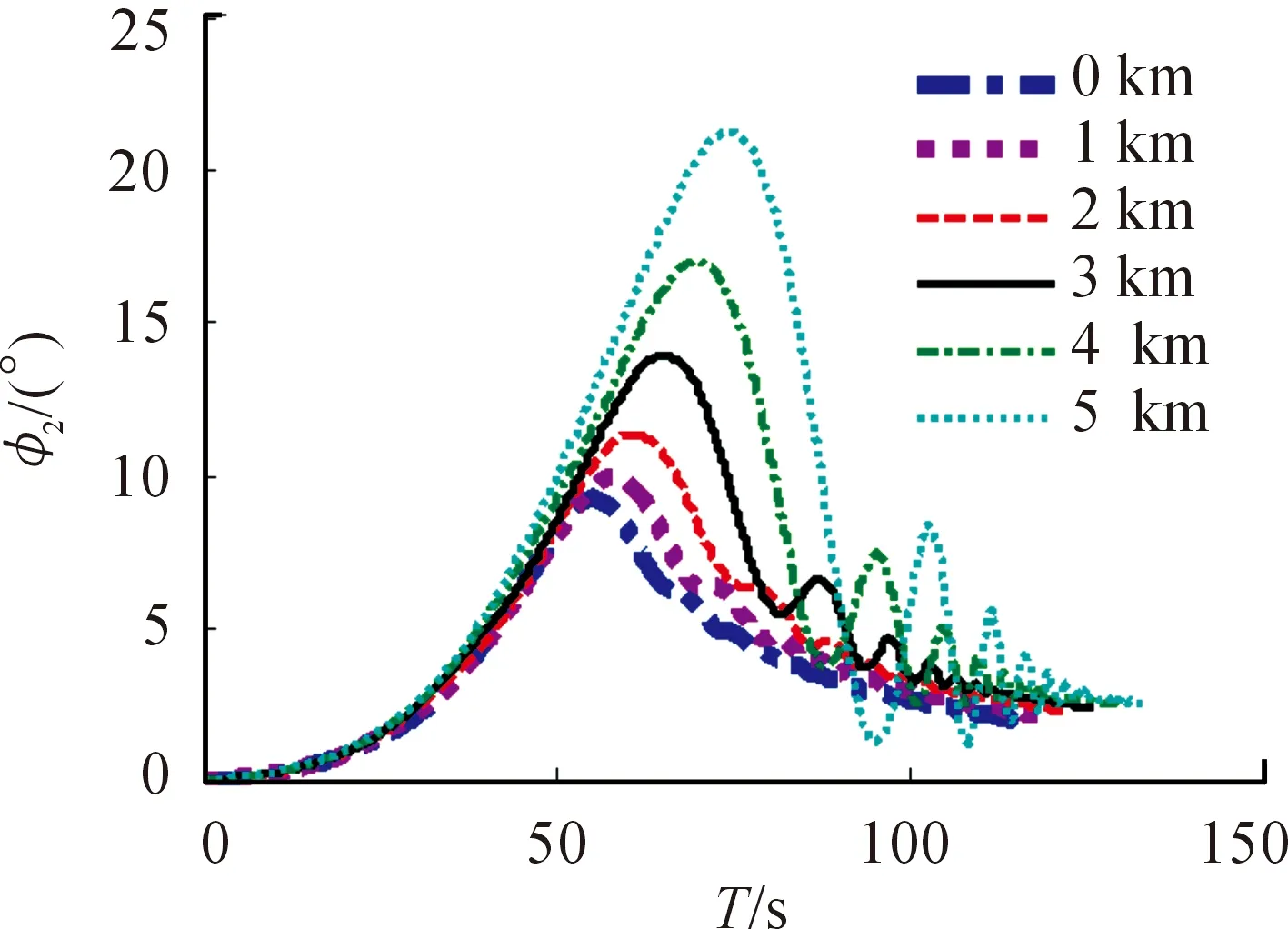
图11 射角60°，弹轴方位角

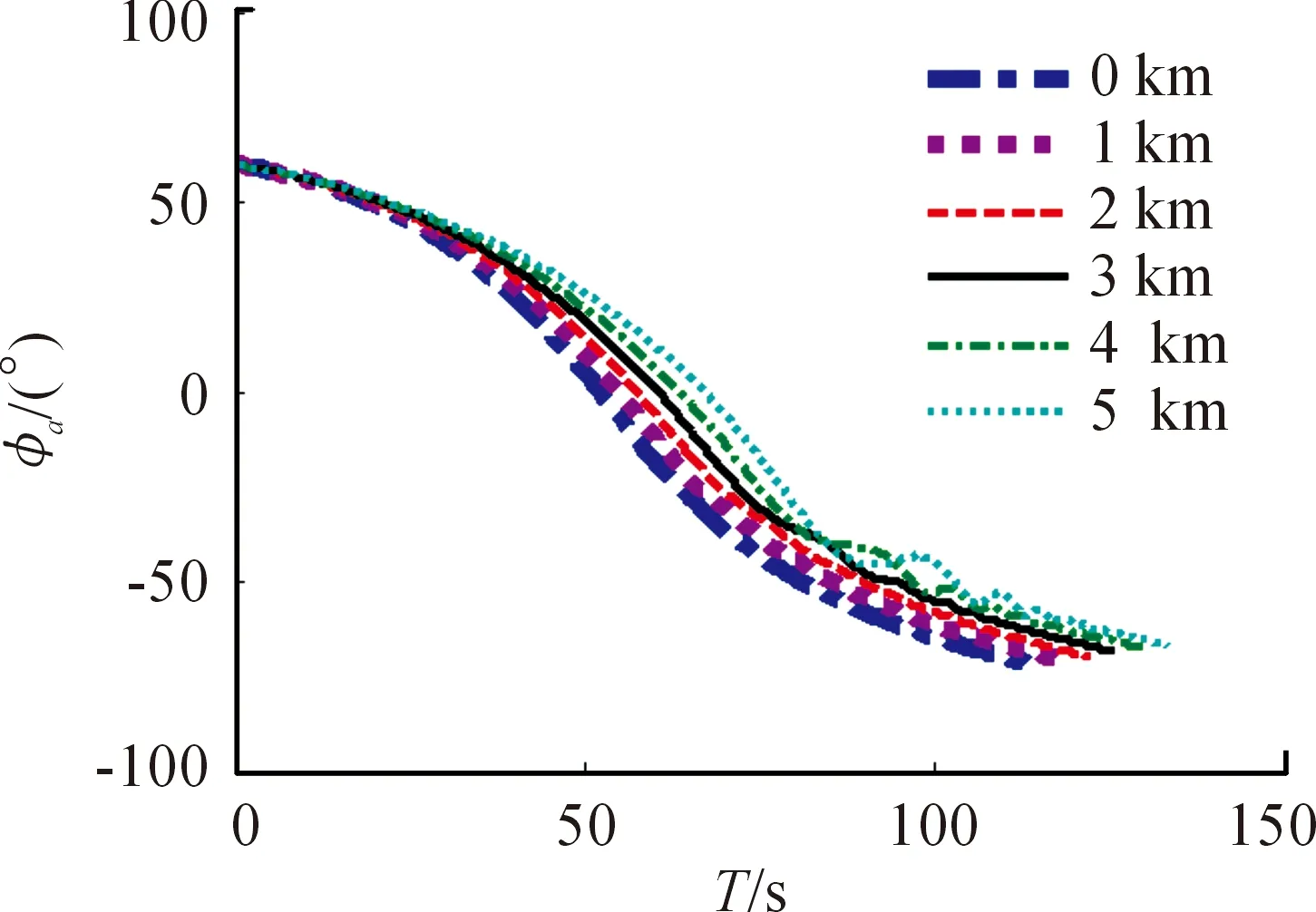
图12 射角60°，弹轴高低角

随着高程的增加，弹轴高低角变化趋势整体变缓，其变化规律与弹道倾角随高程增加的变化规律类似。

2.2.2攻角随阵地高程变化规律

攻角是弹丸飞行姿态中重要的参数，也是考察弹丸飞行稳定性的重要指标。攻角的变化规律随高程的变化情况见图13～图14。

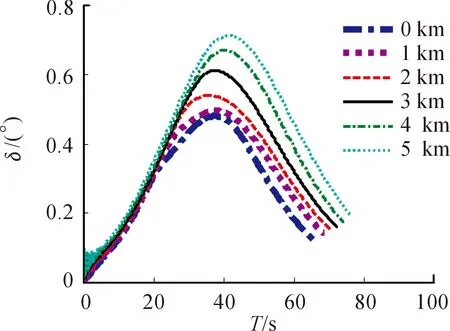
图13 射角30°，攻角

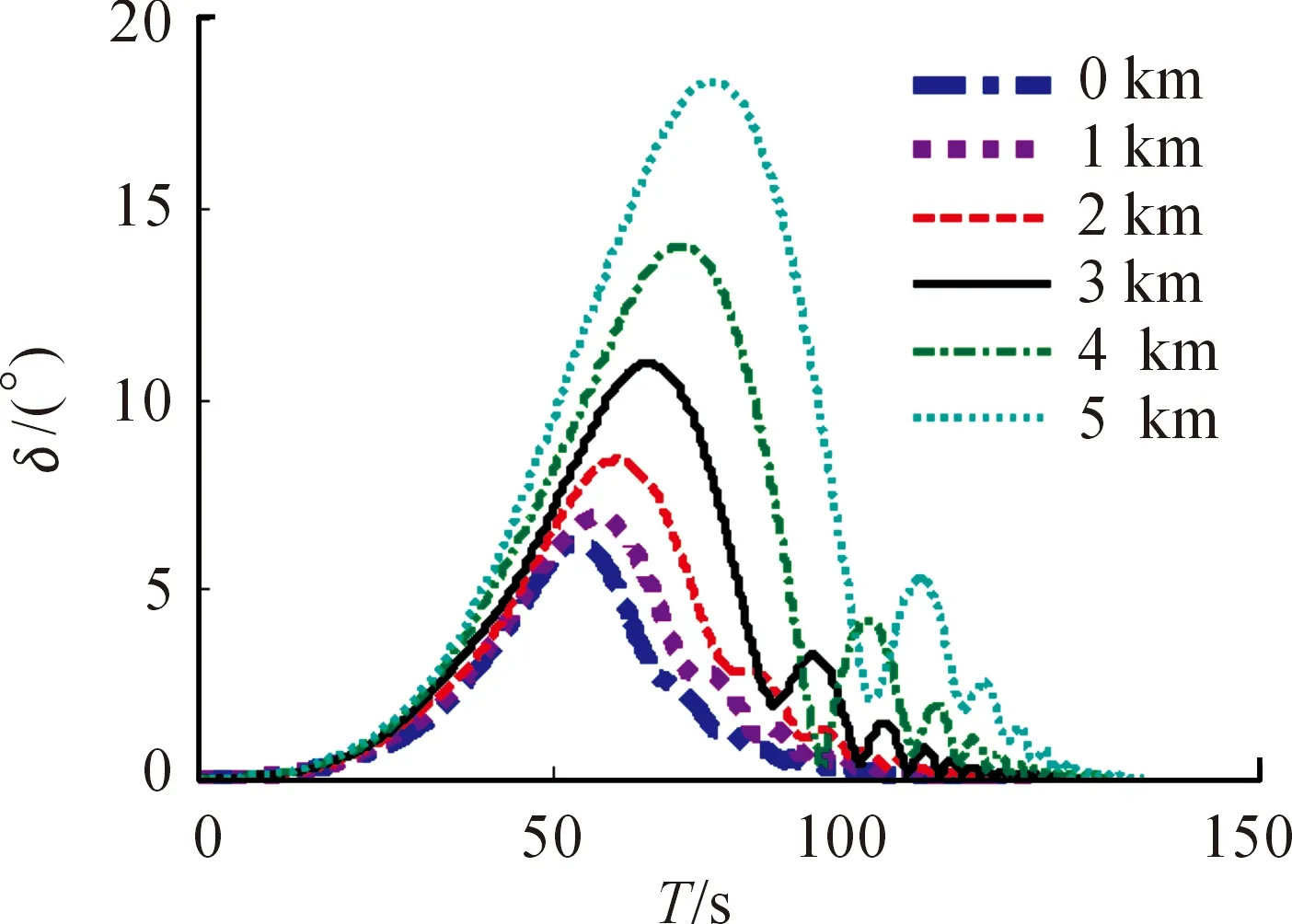
图14 射角60°，攻角

随着高程的增加，攻角变大。以全号装药为例，海拔高度从0～5 000 m，射角30°时，攻角最大值的变化范围为0.47°～0.71°，射角60°时，攻角最大值的变化范围为6.32°～17.64°。此外，射角60°时，攻角在弹道降弧段出现振荡，随着高程的增加，振荡现象越明显。这就说明在高射界射击时，弹丸的高原飞行稳定性变差，高程的增加将加剧稳定性的恶化。

2.2.3转速随阵地高程变化规律

转速随阵地高程变化规律如图15～图16所示。

图15 射角30°转速

图16 射角60°转速

可以看出：高海拔时由于空气密度减小，转速的衰减趋势整体变缓。通过仿真结果也发现，随着射角的增加，衰减曲线出现了两个拐点，即说明转速衰减除了保持起始段衰减较快的特点外，逐渐显现出在弹道中段衰减速度变缓而在末段衰减速度加剧的趋势，如图16所示的60°射角条件，表现尤为明显。这种变化趋势对在弹道末段需要开仓或进行制导控制的弹丸来讲则需要在设计和使用中引起重视。