让学生养成寻根究底的数学探究意识

冯怀勇

【摘要】学生是课堂的主体，如何充分调动学生的主动性和积极性，让他们不仅知其然，更知其所以然。笔者尝试了验证教学。

【关键词】主动 探究 意识

一次，教学六年级“图形放大与缩小”一课时，笔者呈现了这样一道习题：“按2：1的比画出直角三角形放大后的图形。”在教学巡视过程中，笔者发现学生基本是按照“先行放大直角三角形的两条直角边;接着，在放大后的两条直角边的端点处连线，形成放大后的斜边”这一步骤方法进行画图。对此，笔者问学生：“画出的两条直角边是不是按一定的比在放大？”他们不仅做出肯定的回答，还从数据分析的角度给出理由;然而，当笔者再次追问学生“三角形的斜边是不是也按一定的比放大？”这一问题时，学生只给出了两个字当然。

“当然”有笃定、应当这样的含义。依据教师理解，学生使用“当然”一词笃定直角三角形的斜边也在按比放大，显然缺少了一些分量，一些必然。根据教学判断，学生使用连线来画斜边，这种做法只能看成是一种画图技巧，不能成为解释的理由。数学教学倡导学生认知理解的科学精神和态度，为此，笔者展开了如下的验证教学，试图引导学生在探究中理解为什么可以这样画斜线的道理。

案例回放

学生展示了按2：l的比放大后的直角三角形，并说明了其是先按比放大直角三角形的两条直角边;接着，在放大后的两条直角边的端点处连线，画出了放大后的斜边，形成放大后的直角三角形。

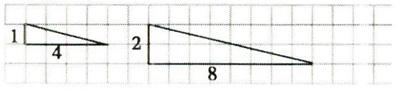
师：画出的两条直角边是不是按2：l放大？

生：放大前，短直角边的长度是lcm，长直角边的长度是4cm;放大后短直角边长度是2cm，长直角边的长度是8cm。它们的长度都扩大了2倍。

师：那图上的斜边是不是也是按照2：1放大呢？

生：当然。

师：为什么呢？

学生们面露难色，有了疑惑。

师：这样，同学们一起来想办法验证一下，在两条直角边上连出的斜边是不是也按2：1放大。

学生自主探究完毕后开始汇报。

生l：我量了两条斜边的长度，原来直角三角形的长度是2.9cm，放大后的斜边的长度是5.8cm，斜边是按2：1放大。

生2：我看了斜边经过的格子数，发现原来的斜边经过4格，放大后的斜边经过了8格，8比4等于2，斜边也是按2：1放大。

生3：我是将放大后的三角形分成4個与原图相等的小三角形，这时，放大后的三角形里有两条斜边，因此，斜边是按2：1放大。

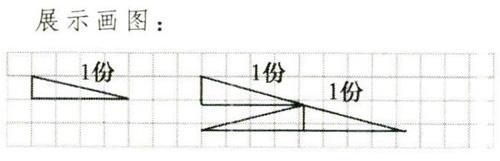
师：这样的做法很有意思。从这两幅图中确实能看出斜边的比是2：1.同时也说明对应边的比都是2：l。

生3：我还发现放大后的三角形与原图形的面积比是4：1。

师：那么，放大前后的三角形的面积比是不是4：1？为什么？大家有时间，可以课下去试着验证。

回过头，笔者问起那位说“当然”的学生“你现在知道为什么斜边也是按2：1放大”时，他点了点头。

学生经历了放大前后的斜边关系的探索过程，他们展示了度量长度、数格子、画三角形等多样化的方法，这时，再去问他们“斜边是不是按2：1的比放大？”这一问题时，他们不仅能说“当然”，更能从不同的角度去证明。

数学知识中存在许多像学生所说“当然”的情况。如：三角形的两边之和当然大于第三条边;5的倍数里当然有5;在折线统计图上当然能看出数最的增减变化，等等。上述的理解表达有其合理性，但这样的认识并不是“想当然”的，而是基于数学的演绎和证明。“放大前后的斜边关系”验证教学过程的最大意义在于：要使学生对事物的认识不能仅停留于“当然”的层面，而要从认知的本源出发，学会去追因、究理，使他们知“其然”，更知其“所以然”，这样才能做到真正的理解和融会贯通。

那么，当学生只是存在肤浅的认识，出现只知“其然”，不知其“所以然”的情况时.教学应怎样处理呢？对此，笔者认为教师应使用如下的教学策略帮助学生获得真正的理解，以此培养学生寻根究底的数学意识。

1.紧扣学生主观表达，把握探究活动契机

教学中，学生时常会使用诸如就是、一定、当然等带有主观性的词语来表达观点，这种表达方式看似有力，一旦缺乏有效的证据支撑时，这些主观表达就显得苍白无力了。对此，教师应有意识地紧抓不放，通过有效的追问看清学生是否存在认识不足、理解不够等问题，以此建立新的探究契机，促成认知的再深化。在“图形的放大与缩小”教学中，学生在说明所画直角三角形斜边的关系后，很确定地认为斜边当然是按2：1放大，这时只需轻巧地问一句“为什么”，就能看出学生是否真的弄明白特殊边长的放大成因。当学生面露难色，不明就里时，即是促成个体理解的关键机会。

2.组织自主验证活动，展示个体多元思考

验证教学的过程应发挥学生的自主性，同时兼顾个体的认知差异。在“图形的放大与缩小”教学中，课堂上布置学生思考“斜边是否也按一定的比放大”这一验证任务，并要求他们自主探索验证。教学反馈显示，有的学生通过测量放大前后的斜边的长度，计算得出斜边是按一定比放大;有的学行是通过对比斜边所占格子数，发现斜边是按一定比放大;有的学生则是用原图形分割放大后的图形，从而明确两条斜边之间的关系。上述自主验证活动具备如下优势：其一，避免教师牵着走，使得学生验证能力和经验快速提升;其二，避免验证方式的单一化，使学生从多元视角理解斜边为什么会按比放大，怎样放大背后的“所以然”。

3.留意衍生教学发现，养成认知理解习惯

教学应注重培养学生“知其然，更知其所以然”的认知习惯，使学生在不明就里时，能自发地想办法弄明白。对此，教师应做个有心人，留意学生的认知生成，通过合理的引导，将有价值的生成性知识转化成探究的问题，养成学生凡事究理习惯。在“图形的放大与缩小”教学中，当学生经历探究过程明确了变化前后的斜边确实按2：1放大后，有学生提出了“放大后的三角形与原图形的面积比应是4：1”的观点。这一观点显然不是这节课所学的对应边变化，然而却可以作为探究的问题，成为培养学生理解能力的机会，帮助发现图形之间变化的另一种规律。

数学教学讲求通法、明理。在学生深入理解一个知识、一个问题或一个现象时，需要鼓励其多问几个“为什么”，一旦弄明白其中的道理，数学知识的呈现才是理所当然，学生也能在此过程中产生寻根究底的数学探究意识。