思茅松天然林单木含碳量空间异质性分析

刘 畅 胥 辉 欧光龙

( 西南林业大学林学院，云南 昆明 650233)

森林对二氧化碳含量下降有着重要的作用，它可以减缓全球变暖，减少全球变暖带来的影响，是陆地生态系统的最主要碳汇，可维持碳循环的基本平衡[1-3]。森林碳汇已经成为了国内外环境学者研究的热点，目前大部分学者对森林碳汇的研究集中在定量问题上[4-5]，并提出了很多的方法。常用的主要有两种，第一种是利用生物量来推算碳储量[6]，第二种是利用气象方面的原理以及技术来测量森林的二氧化碳通量，再将它转换成碳储量[7]。对于国内的大部分学者，经常使用的是第一种方法，但是由于关于森林的碳汇数据都是在不同的地理位置上得到的，不同的坐标、变量之间的关系和相互相影响必然会不同，即为空间的非平稳性，这种空间非平稳性必定会影响碳储量的推算结果[8]。

空间的异质性是常用来描述空间非平稳性的指标[9]，针对森林的碳汇数据，空间异质性表现为空间结构和空间变异两个方面。空间结构是森林的碳汇在空间上呈现出的各种排列形式，空间变异则为区域化的碳含量在空间上的变异程度。变异函数是一种很好的描述空间异质性的方法，已经有很多学者对此进行了研究[10]。万丽[11]运用变异函数，对数据的空间变异性从变异函数的参数特征、各向异性比以及分维值三个方面给出了定量描述的方法，并指出变异性是定量描述中不容忽视的尺度效应。温兆飞等[12]用该方法对农田景观的空间变异性进行了研究，并取得了很好的效果。魏凤英等[13]利用变异函数对降水场的空间特征进行了分析，也取得了较好的效果。

由于对森林碳储量空间问题的研究较少，尤其是在单木含碳量的空间格局研究上鲜有报道，因此本研究以云南省普洱市澜沧拉祜族自治县思茅松天然林为研究对象，对其不同尺度的单木各器官含碳量的空间异质性进行研究，并分析关于单木含碳量的空间格局研究的最优尺度，这对及时准确地获取区域森林碳储量的分布信息以帮助管理者更好的对森林进行经营管理具有重要意义。

1 研究区概况

研究区为云南省普洱市澜沧拉祜族自治县，县境位于云南省西南部，地处东经 99°29′～100°35′，北纬 22°01′～23°16′，因东临澜沧江而得名。澜沧县总面积8 807 km2，为云南省县级面积第二大县，地处横断山脉怒山山系南段，地势西北高、东南低，五山六水纵横交错，海拔600～1 700 m的宽谷、盆地周围低山、丘陵及河流两岸山地，山区、半山区占98.8%。年平均温度17～22 ℃，年降水量1 500 mm以上，相对湿度80%以上。林木类主要有思茅松（Pinus kesiyavar.langbianensis）、水冬瓜（Adina racemosa）、木荷（Schima superba）和各种栎类（Quercussp.）、竹类，以思茅松和栎类为多。

本研究的对象即为该区域内的主要树种思茅松。思茅松是松科（Pinaceae）松属（Pinus）常绿乔木，主要速生用材树种之一，是中国亚热带西部山地林木的代表类型。在土壤深厚、光照充足的单纯林下，生长迅速，更新良好。思茅松为喜光树种，深根性，喜高温湿润环境，不耐寒冷，不耐干旱瘠薄土壤[14]。

2 研究方法

2.1 样木调查

本研究所使用的数据来源于2013年思茅松样地调查数据，结合当时进行的样地调查并考虑径阶分布，在研究区内共计调查思茅松天然林标准木37株，样木分布见图1。每株样木分别记录地理位置（GPS坐标）、地形特征（海拔、坡度、坡向、坡位等），林分因子（年龄、胸径、树高、冠长、冠幅等），同时记录对象木5 m范围内的邻近木情况。

图 1 样木分布Fig. 1 Distribution of samples

2.2 含碳量计算方法

生物量测定采取分器官分别测定，主干部分采用材积密度法测定生物量，将伐倒木分段测定长度、直径等因子，套算材积，分段称取鲜重并取样；枝、叶采用分级标准枝法进行测定；枯枝、嫩叶、果实采用全称重法；根系采用全称重法测定，记录主根根长及基径，主根生物量分段称重并取样，侧根全称重并取样。将烘干的树干、树枝、树叶、树皮、树根及枯枝等样品用打磨机磨碎，进行处理后用C/N分析仪测量各样品的含碳率，分别乘以各器官生物量计算含碳量。样木含碳量统计结果见表1。

表 1 样木含碳量基本统计表Table 1 Basic statistics of carbon content of sample

2.3 变异函数

2.3.1 函数定义

变异函数是描述随机场和随机过程空间相关性的统计量，被定义为空间内两空间点之差的方差。在实际应用中，由于无法遍历空间内所有点，通过有限个采样计算的变异函数被称为经验变异函数。变异函数是建立在二阶平稳假设基础上的一种空间变异结构分析工具，经验变异函数被定义为：

2.3.2 主要参数

块金值（Co）、基台值（Co+C）、变程（a）和各向异性比K（h）是确定变异函数的主要参数。根据相关的理论，随着间隔距离h的增大，变异函数从非零值达到一个相对稳定的常数时，该常数称为基台值，基台值表示系统属性或区域变化量最大变异，基台值越大表示总的空间异质性程度越高，也是研究空间异质性最重要的一个指标。变异函数达到基台值时的间隔距离称为变程，变程是区域变化量的空间变异尺度，当采样间隔距离大于a时，变量与空间不相关，即变程是采样面积的临界尺度，小于变程的采样尺度也不能真实地反映变量空间异质性。当间隔距离h=0时，=Co，该值称为块金值，块金值的大小可以反应区域变化量的随机性大小，也就是随机部分的空间异质性，较大的块金值表明较小尺度上的某种过程不可忽视，当样地面积过小就会出现纯块金效应，从而不能真实地反映空间异质性。变异函数的大小与距离和方向有关，表示了区域化变量随着空间位置和方向不同所产生差异的大小。在计算实验变异函数的时候，尺度的选择要适中，太大则包含了很多无用的随机信息，太小则可能导致区域化变量的变异和空间结构信息不能完全被探测到[15]。

在本研究中，选择了4个方向上最大的距离400 m作为最大变异，以50 m为间隔依次减少，分别计算全向及南—北、东北—西南、东—西和西北—东南方向的变异函数，进而研究思茅松含碳量随尺度变化的空间异质性及方向对其的影响。

2.3.3 函数模型

变异函数模型有很多，常用有球状模型、指数模型、高斯模型、幂模型及线性模型等，其在不同的实际应用中不同的模型选择也会出现不同的效果。针对本研究的数据，经过实验，球形模型更为适合本研究的拟合，其形式如下：

3 结果与分析

3.1 思茅松单木含碳量空间异质性组成及尺度效应

空间异质性主要由两部分组成，即随机部分和自相关部分[16-17]，块金值与基台值之比（Co/（Co+C））表示随机部分的空间异质性占总空间异质性的程度，剩余则为空间自相关性引起的。因此，为了确定思茅松单木含碳量的空间异质性的组成及在不同尺度上变化，以50 m为间隔分别计算了从50～400 m的全树含碳量的全向变异函数的块金值、基台值及块金值与基台值之比，见图 2～4。

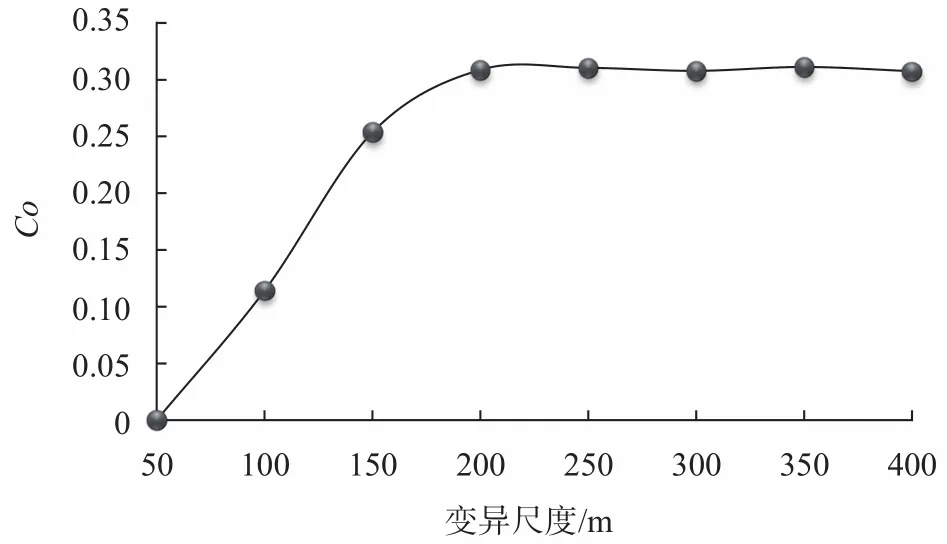
图 2 思茅松单木全树含碳量块金值尺度变异Fig. 2 The scale variation of the carbon content of the individual tree of P. kesiya var. langbianensis

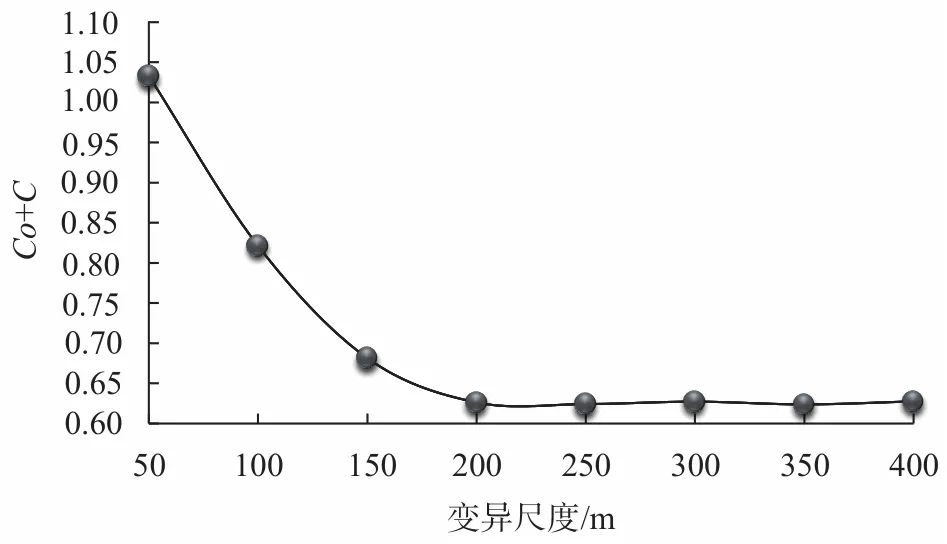
图 3 思茅松单木全树含碳量基台值尺度变异Fig. 3 Scale variation of carbon content in the individual tree of P. kesiya var. langbianensis

由图2可知，思茅松单木全树含碳量在全向时，块金值会随着尺度的增加逐渐加大，并在200 m时，趋于平稳，说明思茅松单木全树含碳量的随机性会随着尺度的增加而增大。由图3可知，基台值会随着尺度的增加而减小，同时也在200 m的时候趋于平稳，说明思茅松单木全树含碳量的空间变异性会随着尺度的增加而减小，且在200 m后趋于同质，表现为随机分布。由图4可知，本研究中思茅松的全树含碳量在200 m的尺度内，自相关引起的空间异质性起决定作用，而200 m后则由随机因素引起。

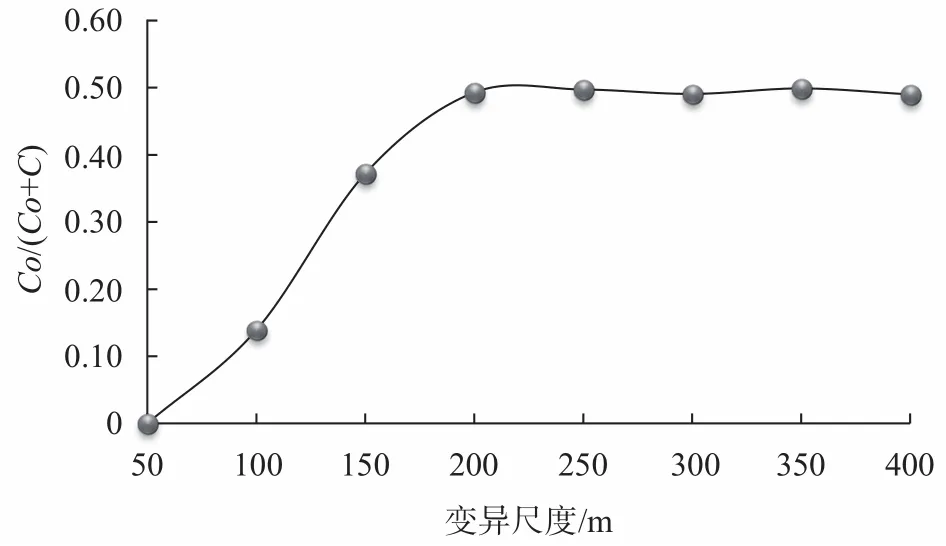
图 4 思茅松单木全树含碳量块金值/基台值尺度变异Fig. 4 Variation of nugget variance /sill of carbon content in individual tree of P. kesiya var. langbianensis

3.2 思茅松单木各维度含碳量全向空间异质性分析

思茅松单木全树含碳量具有空间尺度效应，而基台值可以表示空间变异性的大小，进而计算思茅松单木各维度含碳量在不同尺度的全向基台值，结果见图5。

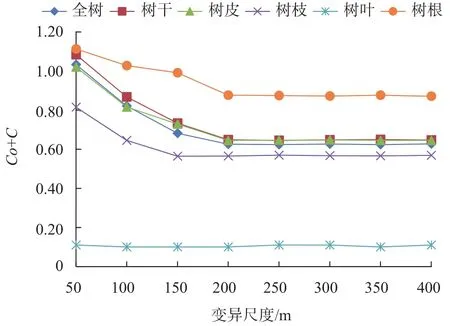
图 5 思茅松单木各维度含碳量基台值尺度变异Fig. 5 Variation of sill of carbon content in different dimensions of P. kesiya var. langbianensis

由图5可知，思茅松天然林单木各维度的含碳量除树叶外，其余维度的空间变异均会随着尺度的增加而减少，最后趋于平稳（拐点为200 m），之后的空间异质性也表现为同质。其中树根的空间变异值最大，即环境的差异对树根的固碳能力影响最大。树根的生长与土壤水分及养分含量均有重要的关系，而尺度环境如坡度、坡向、海拔等的变换，都会导致土壤成分的改变，所以根系生长的空间变异与空间尺度关系较大。对于树干、树枝、树皮、全树来说，空间变异大小差异不大。这些维度会同向生长，即针对本研究的研究区来说，虽然空间异质性会随着尺度的增大而改变，但是这种变化在这些维度上是相似的。即在200 m的范围内，单木各器官的生长大环境是一致的，因而固碳能力的变异也相差不大。而对于树叶维度来讲，计算结果显示出其空间异质性不管在任何尺度，均不会发生改变，即为同质现象。这是由于本研究的研究对象为单木，且树叶相对于其他器官来说碳存储量非常微小，因而导致计算结果差异不大。

3.3 思茅松单木含碳量各维度异向空间异质性分析

为了更好的研究思茅松单木含碳量各维度在不同方向上的变异，分别计算了南—北、东北—西南、东—西和东南—西北方向的基台值，结果见图6。

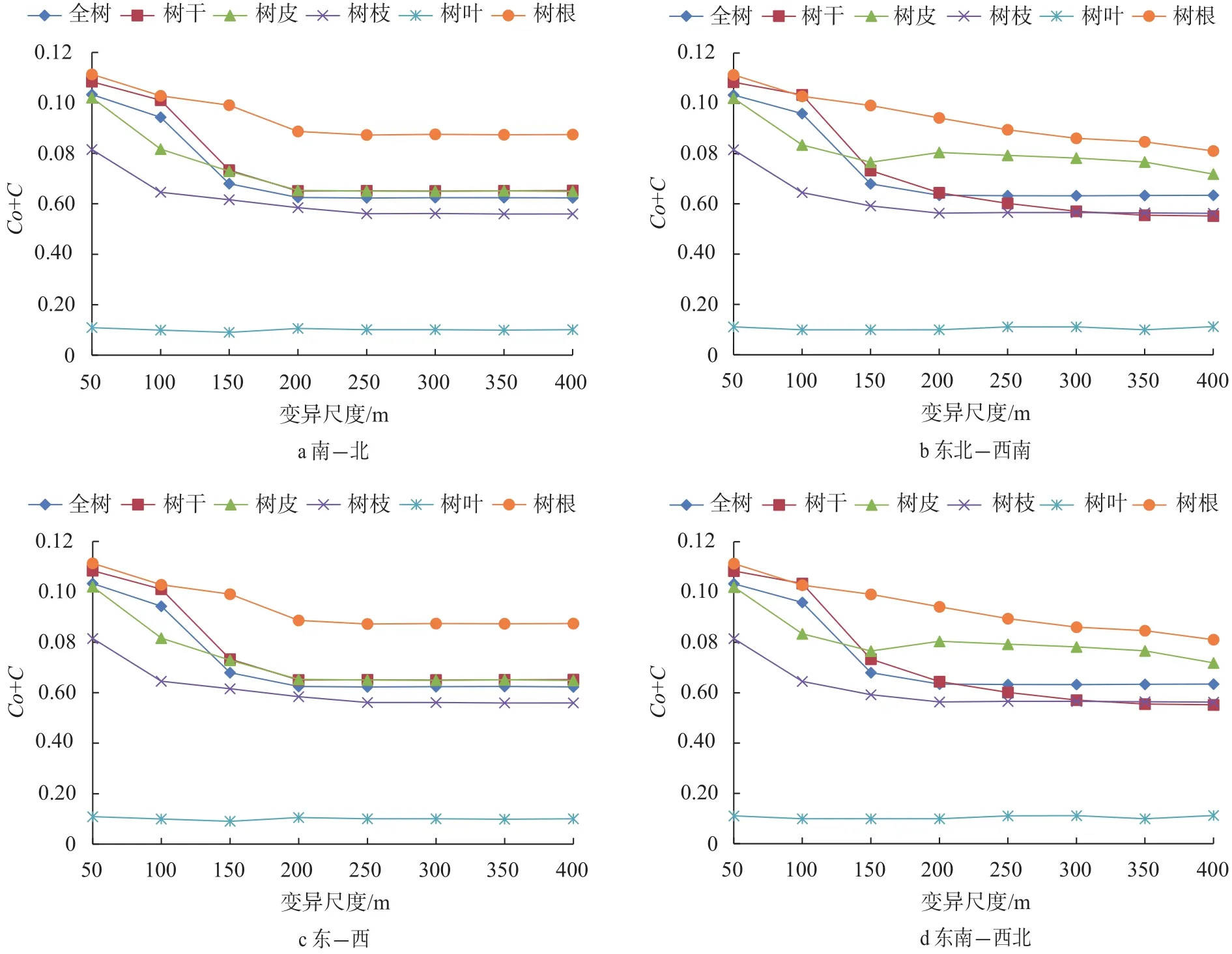
图 6 思茅松单木各维度含碳量异向基台值尺度变异Fig. 6 Variation of different-directional sill of carbon content in different dimensions of P. kesiya var. langbianensis

由图6可知，思茅松除树叶外，其他所有维度，在各个方向上随着尺度的变化空间变异均会随着变化，南—北向与东—西向这种变异呈现相似的变化，且与全向相似；东北—西南向与东南—西北向的变异相似。由此可知，思茅松天然林单木含碳量各维度的空间变异，在南北和东西向的变化在本研究的区域呈现主导变化，即南北和东西向环境差异直接影响着思茅松各维度器官的固碳能力，影响最大的依然是树根。在东北—西南向与东南—西北向，树根无明显的变异拐点，即在这个方向上，树根的空间变异虽然逐渐降低，但是异质性一直存在，并不趋向同质。同时，在该方向上，树皮则呈现出与全向较大差异的变异，尤其在尺度150 m之后。相关研究表明，树皮同样具有光合碳固定的能力，且这种能力会随着温度的升高而加大[18]。对于树皮来说，由于其生长位置的特点，并不如树叶及树枝可以长期接受光能，仅在每日特殊时间特殊方向可以接受，因此在东北—西南向与东南—西北向上，变异程度变大。同样由于树叶本身碳储量微小的原因，因此在各个方向上，与全向均一致，空间变异性最小。

3.4 最优空间格局研究尺度选择

空间异质性是一个尺度的函数，因此对其分析必须要考虑尺度问题。变异函数的变程是描述空间异质性尺度的有效参数，相关研究表明生态系统的功能、过程和格局均与尺度有关。王政权等[19]对红松（Pinus koraiensis）、云杉（Picea asperata）、冷杉（Abies fabri）、枫桦（Betula costata）和椴树（Tilia tuan）的空间异质性特征进行研究，结果显示红松在450 m左右尺度上的生态学过程尤为重要，而其他树种在小尺度（＜100 m）上的生态学过程不可忽视。由此可知，确定和检验树种的空间异质性尺度，有助于认识与该尺度所对应的空间格局和过程的差异，即在空间问题研究时要充分考虑尺度问题。尺度过小，样点间的数据差异会增加，尺度过大，样点间的数据会趋于同质，异质性的程度会减小。此外，尺度的变化也会影响空间异质性的各向异质结构。利用变异函数可以确定空间变异的尺度，进而确定最优的研究范围。本研究中，可以确定本研究区域内思茅松天然林单木含碳量的空间变异除树叶外，均在200 m时趋近平稳，表现为同质的特点。因此在本研究中，拐点200 m是一个很好的研究尺度，在该范围内可以很好的体现出思茅松单木含碳量的空间格局和生态学过程。

4 结论与讨论

针对空间异质性信息对森林碳储量影响的重要性，本研究利用37株思茅松天然林单木各维度含碳量数据，采用变异函数结构分析的方法，对其空间异质性行进了定量分析，并在此基础上探讨研究单木含碳量时最优尺度选择方法，得到如下结论：

1）思茅松单木全树含碳量存在空间异质性，且这种异质性的随机性会随着尺度的增加而增大，并在200 m时趋近于平稳。而空间变异程度则会随着尺度的增加而减少，最后趋于平稳，即在200 m内空间异质性是由自相关引起的，而之后表现为同质现象，说明该尺度之外，思茅松天然林单木含碳量的空间异质性已经为随机因素产生的。

2）对变异函数的拟合分析，可以定量的阐明思茅松单木各维度全向及异向的空间变异性质。针对本研究，树根的空间变异程度在各个尺度上均为最大；树叶由于固碳量最小的原因，因此其空间异质性的表现变化较小。在东北—西南和东南—西北向上，树根的空间变异性质随着尺度加大逐渐降低，且无明显拐点；树皮呈现出与全向有极大差异的空间变异，说明方向对树皮固碳能力的影响较大。

3）通过变异函数对空间异质性的定量表达，可以确定空间变异的程度随尺度的变化趋势，进而寻找最佳的空间格局研究尺度，即变异函数的拐点处。

在研究生物问题时，均会存在空间效应，即表现为空间相关性和空间异质性，而且这种效应会随着尺度的变化而发生改变，有很多的学者对此进行了相关的研究，并提出了很多办法[20]。本研究则提出使用变异函数的方法对思茅松天然林各维度含碳量的全向及异向空间异质性进行研究，得到了较好的效果，并可以以此解决空间格局研究尺度的问题，因此在日后的研究中可以考虑使用该方法对森林碳储量的相关问题进行研究。