高速永磁电机转子动力学特性研究

黄金平，张峥岳，黄道琼，宴才松，薛 杰

(1.液体火箭发动机技术重点实验室，陕西 西安 710100;2.北京航天动力研究所，北京 100076；3.中车株洲电机有限公司，湖南 株洲 412000)

0 引言

为了减少涡流损耗，永磁电机转子一般采用硅钢片叠压结构，由于结构自身限制，某些电机转子还会采用拉杆固定和连接叶轮，这些结构特点均会改变转子自身的弯曲刚度，给转子的动特性分析带来新的挑战[1-2]。在进行动特性分析时，为建立精确的轴系有限元模型，目前常用的方法是依据试验模态频率和振型共同进行模型结构参数的修正[3-6]，这种建模方法及分析结果的准确性完全依赖于试验结果，而单独有限元仿真结果的可靠性在一定程度上有所下降。为提高仿真结果的准确性和可靠性，本文针对电机转子中硅钢片叠压及拉杆-叶轮的特殊结构形式，通过有限元方法模拟硅钢片叠压结构装配过程，获得硅钢片叠压结构横向弯曲刚度随硅钢片离散数目的变化规律，通过曲线拟合外推得到实际硅钢片叠压结构横向弯曲刚度；根据叶轮与转轴对接面的大小，对叶轮进行分割。以质量和刚度等效为原则，建立了精确的轴系有限元模型，并通过模态试验对模型进行了验证。在此基础上，对电机轴系的前三阶临界转速进行了仿真分析，并在试验台上进行了最高至12 000 rpm的运转试验，结果表明前两阶临界转速的仿真和试验结果具有较高的吻合度。

1 永磁电机转子结构

某高速永磁电机转子结构简图如图1所示，两端悬臂叶轮通过中心拉杆与转轴连接，为提高运行稳定性，转子采用五叶可倾瓦滑动轴承支承，叶轮1端为推力轴承，叶轮2端为径向轴承。跨中为由厚度不超过0.5 mm的硅钢片叠压组成的永磁结构。与传统的整体式或串式转子结构相比，该永磁电机转子叶轮的拉杆连接方式及硅钢片叠压结构会对转子整体的动特性有较大影响。在进行动特性分析时，需对转子结构进行专门的简化处理。

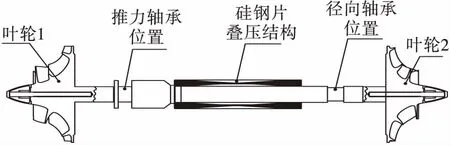
图1 永磁电机转子结构示意图Fig.1 Rotor structure diagram of the permanent magnet motor

2 电机转子模型

2.1 硅钢片叠压结构

2.1.1 硅钢片叠压结构简化及建模

硅钢片叠压结构由单片厚度不超过0.5 mm的一组硅钢片叠压成型，如图2所示。硅钢片叠压结构装配过程：1)通过轴向贯通的12片磁钢片将所有硅钢片串接；2)采用专用工装通过两端压板给硅钢片组施加轴向预紧力；3)在2)的基础上，两端压板、硅钢片组与转轴过盈装配；4)拆除轴向预紧力加载工装，完成装配。

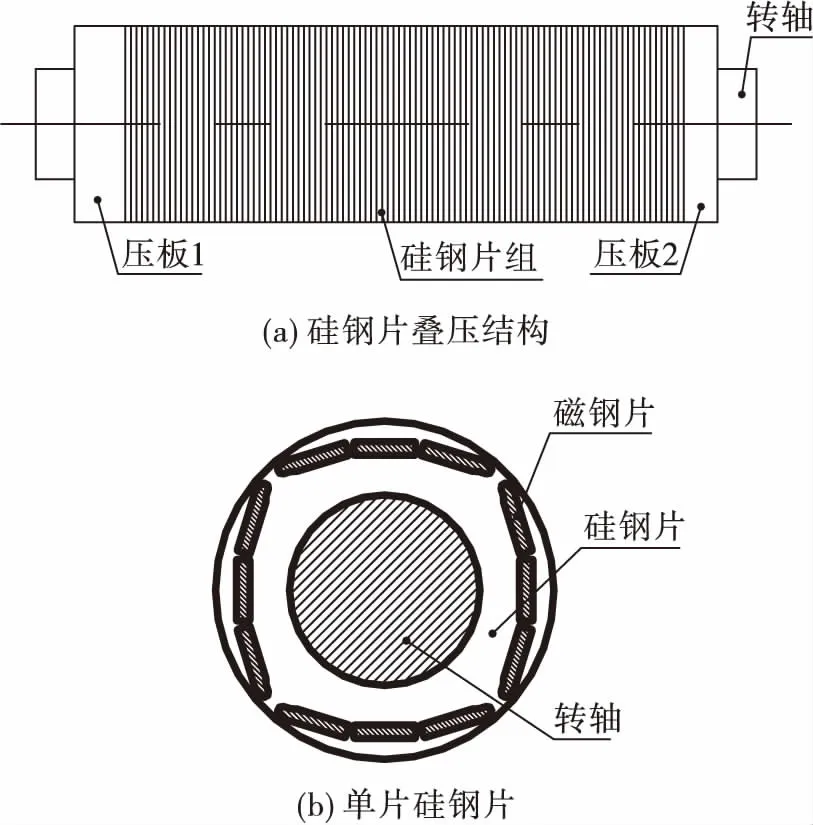
图2 硅钢片叠压结构Fig.2 Structure of silicon steel sheet lamination

硅钢片的装配状态对转轴的横向弯曲刚度有明显影响，根据装配过程对硅钢片组及转轴的横向弯曲刚度进行仿真分析，在保持结构尺寸不变的情况下通过质量和刚度等效原则，对硅钢片叠压结构进行简化。

分析模型的边界条件：1)约束图2中转轴的两个端面，各相邻硅钢片之间、各硅钢片与磁钢片间、磁钢片与压板之间及硅钢片与压板间均建立接触关系；2)硅钢片、两端压板分别与转轴之间建立过盈装配关系。

实际电机转子硅钢片数目在103量级，接触对数目在1.5×104量级，采用全模型仿真基本无可行性。为提高仿真效率，本文提出一种硅钢片整体结构逐步离散逼近的方法来分析叠压结构的弯曲刚度，首先借助有限元方法[7]分析获得硅钢片叠压结构横向弯曲刚度随硅钢片整体结构离散数目的变化规律，然后通过外推方法得到实际硅钢片叠压结构的横向弯曲刚度。

根据装配工艺过程，通过两个载荷步对硅钢片叠压结构横向弯曲刚度进行求解，各载荷步对应的加载过程如图3所示：1)载荷步1中，在求解步0～0.05内完成轴向预紧力的加载，在求解步0.05～0.5内保持轴向预紧力不变，求解步0.5～0.7内轴向预紧力卸载为0并保持至载荷步1结束；在求解步0～0.1内两端压板、硅钢片组与转轴无过盈量，求解步0.1～0.4内过盈量施加到位并保持至载荷步1结束。2)载荷步2中，轴向预紧力完全释放，过盈量保持不变，同时在硅钢片组轴向中心截面上施加侧向强迫位移。根据强迫位移及支反力获得结构横向弯曲刚度。

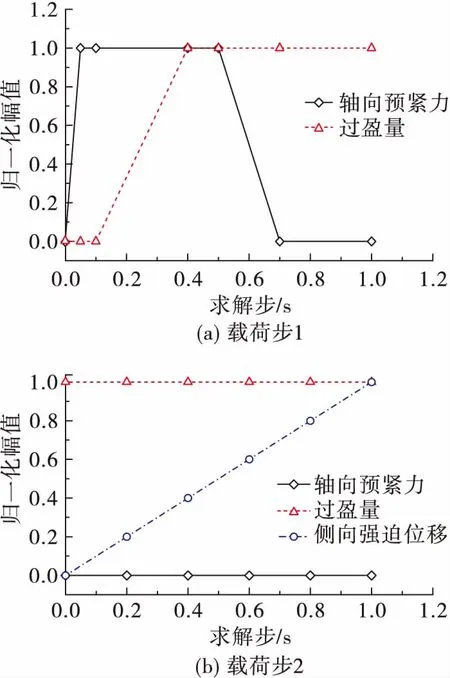
图3 加载过程Fig.3 Loading procedure

结合电机转子具体结构参数，得到硅钢片叠压结构整体横向弯曲刚度K与硅钢片整体结构离散数目n的变化关系(见图4)，通过曲线拟合得到如下关系

K=1.187 5×109n-0.146 93

(1)

在式(1)中输入实际硅钢片数目可获得叠压结构的横向弯曲刚度，通过质量和刚度等效原则，得到该叠压结构的简化结果。

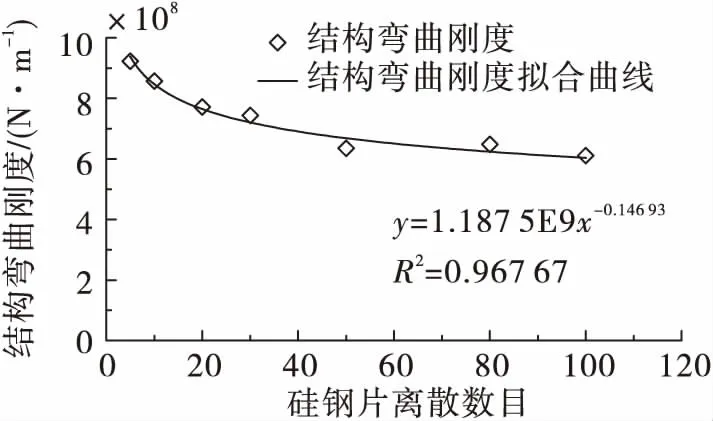
图4 硅钢片叠压结构弯曲刚度与硅钢片整体离散数目关系曲线Fig.4 Relationship between bending stiffness and whole discrete number for SSSL structure

2.1.2 硅钢片叠压结构简化模型验证

为验证硅钢片叠压结构简化模型的准确性，将电机转子系统两端的导流锥、叶轮及拉杆等零部件拆除，只保留转轴部分。通过弹性绳将转轴进行水平吊装，如图5所示，通过锤击法获得转轴的自由-自由模态频率，与仿真结果进行对比，验证仿真结果的可行性和准确性。硅钢片叠压结构分别采用本文方法、整体模型(方法I)和集中质量(方法II)模型简化处理，分析得到自由状态下前三阶频率列于表1中。

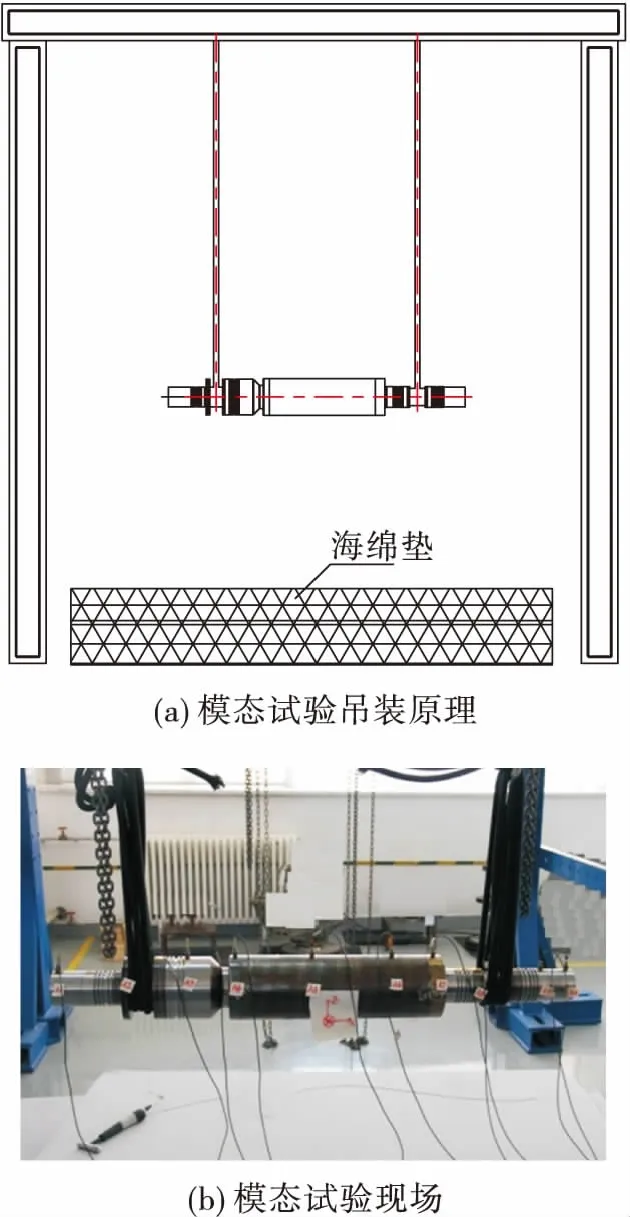
图5 转轴自由模态试验Fig.5 Free modal test of rotor shaft of motor

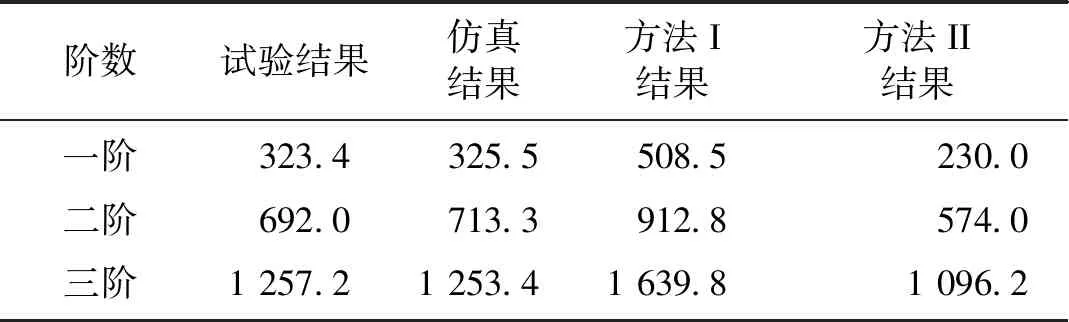
表1 转轴自由模态频率仿真与试验结果比较Tab.1 Comparison between simulation and experimental results of free modal frequency of rotor shaft Hz

硅钢片结构的不同简化处理方法分析结果对比发现，整体结构模型对转轴的横向弯曲刚度有强化作用，因而仿真获得的各阶固有频率与试验结果比较均明显偏大；集中质量模型对转轴的横向弯曲刚度有一定减弱，对应的各阶固有频率偏小；而本文的简化方法采用质量等效和刚度等效的原则，求得的频率与试验结果最为接近，前三阶频率误差均小于3.1%。

2.2 拉杆-叶轮结构简化

2.2.1 拉杆-叶轮结构简化

叶轮采用拉杆连接，在拉杆的轴向预紧力作用下，叶轮轮毂对转轴横向弯曲刚度有增强作用，因此将叶片与轮毂分别进行独立建模：根据叶轮与转轴对接面的大小，将叶轮按图6进行分割[8-9]，导流锥及叶片简化为集中质量，轮毂及拉杆在轴向预紧力作用下根据质量及弯曲刚度相等的原则等效为均匀轴段。

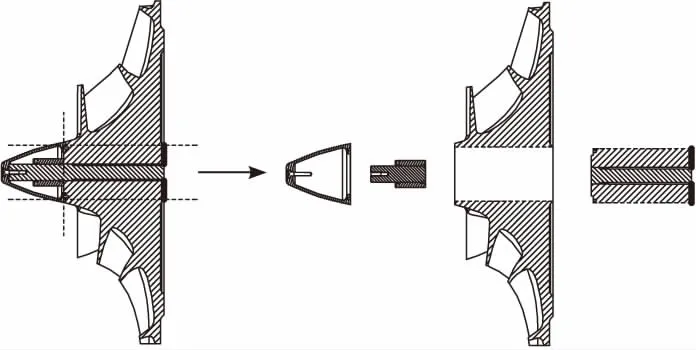
图6 拉杆-叶轮结构简化Fig.6 Simplified structure of nutted-rod impeller

2.2.2 拉杆-叶轮简化模型验证

硅钢片结构简化结果的准确性已通过2.1.2小节的转轴自由模态试验进行了验证，除两叶轮轮毂的简化结果与实际可能存在差别外，其余结构及材料参数与实际基本吻合。这是由于叶轮通过轴端的拧紧螺母进行预紧，轮毂对转轴横向弯曲刚度的增强作用与预紧力大小、接触端面的摩擦系数等有关，而这些影响因素实际中难以精确给定，造成了仿真结果和试验的误差。为此，可通过转子自由状态下的模态试验对模型进行验证和修正。

与2.1.2小节的转轴自由模态试验方法相同，采用弹性绳悬挂的方式对转子进行约束，悬挂点位于两轴承位置，如图7所示。

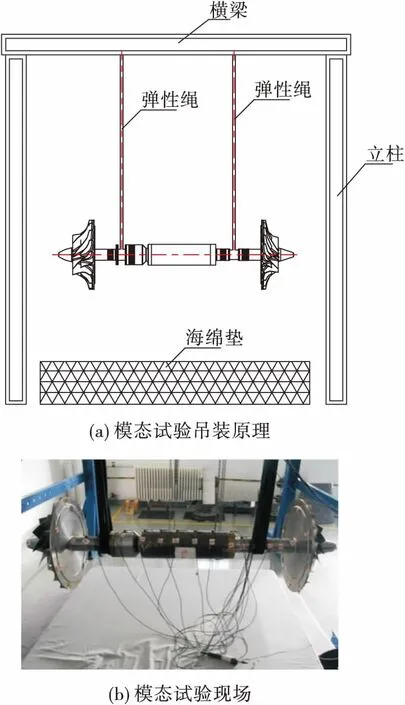
图7 转子自由模态试验Fig.7 Rotor free modal test

模型修正时，以转子的前三阶模态频率为目标，通过调整轮毂及拉杆简化结构的等效弹性模量，使得前三阶自由模态频率的计算和试验结果误差最小。仿真和试验结果对比列于表2中，可看到，模型修正后，转子前三阶自由模态频率的仿真与试验结果的误差均小于5%，且振型吻合度较高。

2.3 轴承模型简化

为提高运行稳定性，转子采用5叶可倾瓦滑动轴承支承，轴承的支承刚度随转速变化，且表现为各向异性。通过滑动轴承仿真软件[10]获得两轴承支承刚度随转速的变化曲线如图8所示。

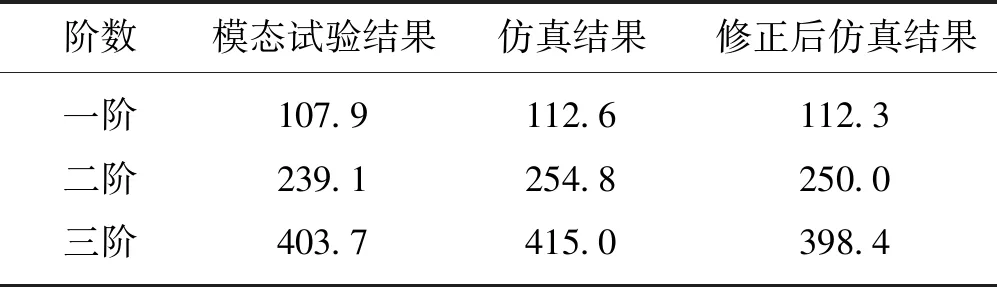
表2 转子自由模态频率仿真与试验结果比较Tab.2 Comparison between simulation and experimental results of rotor free modal frequency Hz

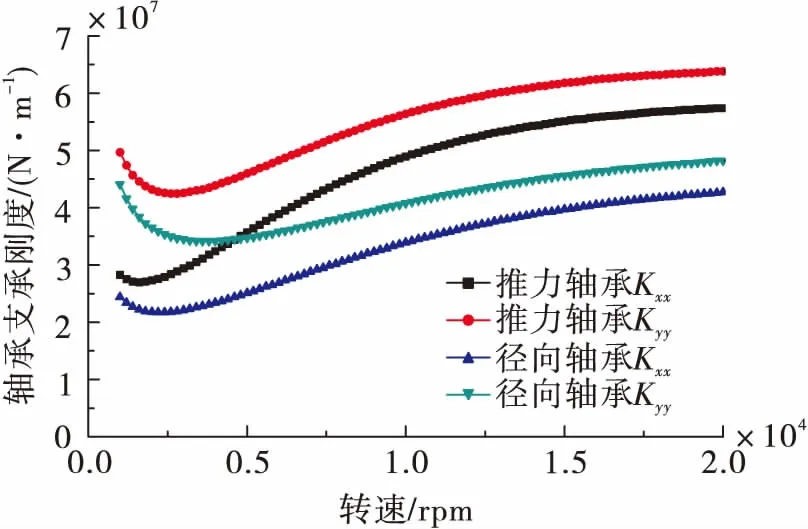
图8 转子轴承支承刚度随转速变化曲线Fig.8 Variation curve of rotor bearing support stiffness with rotating speed

3 临界转速分析

3.1 临界转速仿真结果

对整个转子系统进行结构离散化，建立有限元模型，分析得到Campbell图如图9所示。由于转子的支承刚度各向异性，在Campbell图中表现为静止状态下(转速为0时)正进动(FW)与反进动(BW)的频率具有差异性。剔除反进动结果，获得转子系统前三阶临界转速分别为5 392 rpm，7 884 rpm及20 086 rpm。

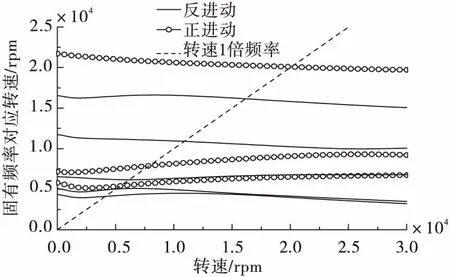
图9 Campbell图Fig.9 Campbell diagram

3.2 试验验证

试验系统如图10所示，转子通过自身轴承支承于刚性底座上，底座的支承刚度远大于轴承支承刚度，在叶轮1端通过膜片联轴器与驱动系统连接，为了减小联轴器对轴系动力特性的影响，联轴器为薄壁轻质柔性结构，自身经过高精度动平衡，且联轴器两端面分别与驱动系统、试验轴系有精确的定位连接。联轴器的这种特性，一方面确保自身质量特性、平衡状态对轴系动特性的影响降到最小，同时将装配和连接带来的影响也控制在较小范围内。

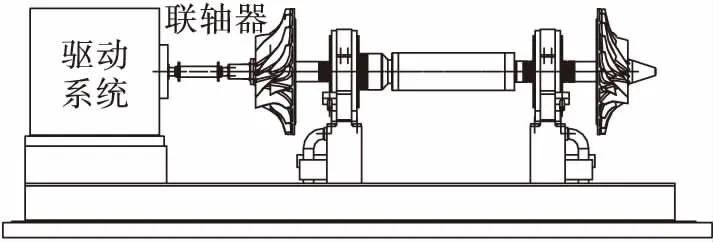
图10 转子试验状态示意图Fig.10 Diagram of rotor test state

轴承采用循环供油方式进行润滑，润滑油入口压力在0.1～0.2 MPa之间，流量不小于10 L/min；除测量振动外，对轴承温升进行实时监测。转子最高升速至12 000 rpm，分别在叶轮1、叶轮2附近两正交方向及转子驱动转接法兰单方向测量转子实时振动位移，经过跟踪滤波后获得同步振动分量(1X)如图11所示。识别出转子的前两阶临界转速分别为5 491 rpm及7 677 rpm，仿真获得的前两阶临界转速5 392 rpm及7 884 rpm与试验识别的误差分别为-1.8%,2.7%，吻合度较高，说明了仿真模型简化方法的可靠性及仿真结果的准确性；同时也证明了工作转速设计的合理性。

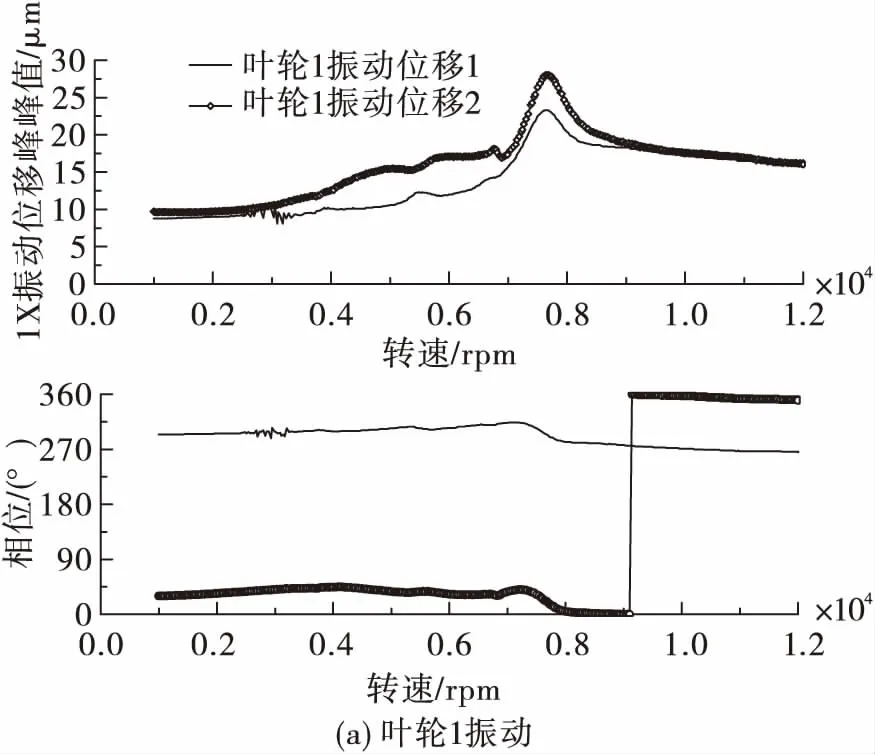
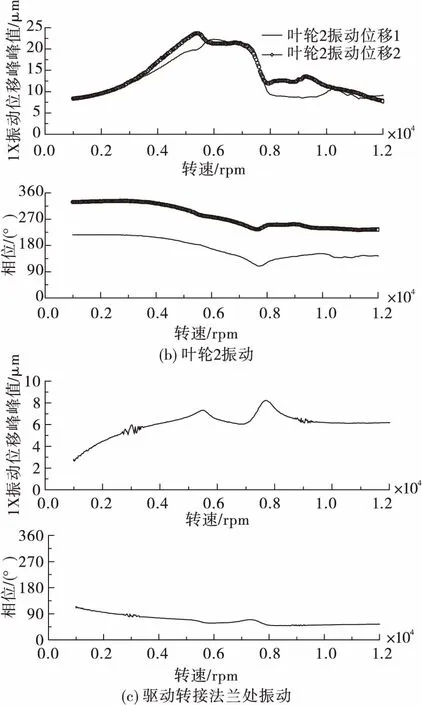
图11 升速过程中转子振动位移1X分量变化曲线Fig.11 Variation curve of 1X component of vibration displacement during acceleration process

4 结论

本文通过仿真和试验相结合的方法对电机转子的动特性进行了分析，得出以下结论：

1)对于电机特有的硅钢片叠压结构及拉杆式叶轮连接结构，在进行轴系动特性分析时必须考虑叠压结构及拉杆连接结构对转轴弯曲刚度的增强作用。

2)在转子动特性分析过程中，硅钢片叠压结构有效的建模方法：结合硅钢片叠压结构的装配过程，根据质量和刚度等效的原则，通过静强度仿真分析，在结构几何尺寸不变的情况下，获得结构密度及材料弹性模量的等效结果，完成该叠压结构的建模，必要时通过模态试验对该建模结果进行修正和验证。

3)通过拉杆连接的叶轮，叶轮轮毂对转轴横向弯曲刚度有增强作用，需根据叶轮与转轴对接面的大小对叶轮进行分割，按照刚度和质量等效的原则对叶轮分割后的各部分进行建模。

4)模态试验和运转试验均验证了本文建模和仿真方法的有效性和准确性，该方法可在同类结构转子中进行推广应用。