高考化学信息型方程式复习备考策略研究
2019-07-02申燕解慕宗徐俊龙
申燕 解慕宗 徐俊龙
摘要: 化学方程式书写既是高中化学核心知识,又是高考的重点和易失分点。根据信息处理方式的不同对近六年新课标Ⅰ卷非选择必做题中的信息型方程式进行分类,并以2018年深圳市高三第二次模拟考试相关数据为参考依据,针对信息型方程式书写提出有效的复习备考策略。
关键词: 信息型方程式; 数据分析; 新课标Ⅰ卷; 复习备考
文章编号: 1005-6629(2019)5-0022-06 中图分类号: G633.8 文献标识码: B
1 引言
化学方程式是学习化学的重要工具,也是化学学科重要的符号语言,它精炼地表述了物质的反应过程。在高中化学学习过程中,方程式的书写占据举足轻重的地位,学生在书写方程式的过程中可以通过符号表征[1]的方式理解化学反应的实质,分析物质的化学性质,精准把握其中量的关系。高考中化学方程式的考查形式多为信息型方程式(或称为陌生方程式),此类方程式的书写并非纯粹的知识点再现,需要考生理解方程式所承载的丰富信息和学科内涵。以信息型方程式的书写为抓手,可以改变通过机械记忆即可得到高分的模式,促进化学观念的内化和学科素养的发展。然而,新情境中的符号表征对考生而言困难重重,故应提升复习的针对性和有效性。
近年来,信息型方程式的书写是新课标Ⅰ卷的考查重点,其考查形式可分为书写离子方程式和化学方程式,考查内容涵盖氧化还原反应和非氧化还原反应。本文基于信息处理方式的差异对近六年新课标Ⅰ卷中的信息型方程式进行归类解析,基于SOLO分类理论[2]分析书写不同类型信息型方程式需达到的思维等级水平,并以2018年深圳市高三第二次模拟考试有关信息型方程式的数据为参考依据,比较三类不同的信息型方程式的难度系数、难度曲线图,探索其中的变化规律与趋势,以期为复习备考提供参考。
2 试题研究与数据分析
信息型方程式在教材中未出现,陌生度高,故考查时在题干中会给予一定的有关该反应的信息,所给信息主要集中在两方面: 物质信息,即主要的反应物、产物信息,与反应相关的物质(如催化剂)信息;环境信息,包括反应能够发生的条件信息(如高温等),反应发生的或物质稳定存在的酸碱性环境信息,氧化还原环境信息(如阳极等)。
2.1 2013~2018年新课标Ⅰ卷信息型方程式分析
按照对信息处理方式的不同,近六年新课标Ⅰ卷中信息型方程式大体可分为三类:
2.1.1 “直接提取”类
此类题目同时给出物质信息(或主要物质信息)以及环境信息,信息的呈现以图像、表格等非文本形式为主,考生需对信息进行有效提取,才能正确作答。如2016年新课标Ⅰ卷第28题(2)要求写出制备ClO2的化学方程式,从流程图中即可获得反应物为H2SO4、 SO2和NaClO3,生成物为NaHSO4和ClO2,以及反应发生的环境信息为常温下的酸性环境。
从SOLO分类理论来看,书写此类方程式时,需要考生从图表中获取物质及环境信息,并应用守恒思想(元素守恒、得失电子守恒、电荷守恒等)将其配平。此过程中,考生能够通过多个未经整合的线索解决问题,故完成该类方程式书写的思维层次属于多元结构(M)水平。
2.1.2 “判断推理”类
在此类方程式题目中,发生反应的环境信息是已知的,而部分主要反应物或产物的信息却是未知的,考生需依据化学学科知识或原理推断出未知物质。如2013年新课标Ⅰ卷第27题(3),由“酸浸”时加入H2SO4和H2O2,可判断反应发生的环境为常温下的酸性环境;此外,考生还需基于得失电子守恒思想对部分未知产物进行推断,根据钴的化合价从反应物LiCoO2中的+3价降为CoSO4中的+2价,得出H2O2中-1价氧的化合价需升高,即可判断出另一主要产物为O2。
对于此类信息型方程式的书写,考生除需从题干中获取反应的环境信息,还需关联各模块的学科知识对未知物质进行推断,根据酸碱环境分析能够与环境共存的物质,再结合守恒思想进行配平。考生在物质推断的过程中使思维产生了逻辑关联,因此相应的思维层次为关联结构(R)水平。
2.1.3 “综合分析”类
此类题目仅给出部分的主要物质信息,而环境信息则以间接形式给出或不给出。如2015年新课标Ⅰ卷第27题(6)要求写出以硼酸和金属镁为原料制备单质硼的化学方程式。考生需对硼酸的性质进行联想、类比和迁移,通过类比与其同主族的铝元素最高价氧化物对应水化物的性质,推断反应发生的环境应为高温,最终判断金属镁转化后的产物。
书写此类信息型方程式时,考生需要根据题目中给出的部分物质信息,推断反应能够发生的环境信息和其他物质信息。考生需超越问题本身形成个性化的推理方式来解决问题,思维层次应达到拓展抽象(E)水平。
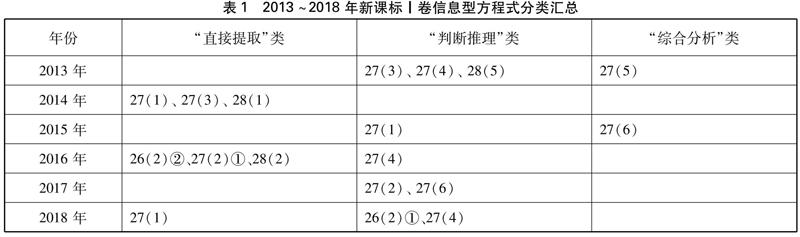
从SOLO分类理论的角度可以看出,三类信息型方程式对考生思维水平的要求逐级上升。基于以上分析,笔者对近六年新课标Ⅰ卷非选择必做题中的信息型方程式进行分类汇总,其统计结果见表1。
近六年新课标Ⅰ卷出现的信息型方程式主要集中于“直接提取”和“判断推理”两种类型,而对“综合分析”类方程式书写考查较少,反映了新课标Ⅰ卷重点考查学生必备的核心知识和关键能力,要求学生具备化学基本观念、掌握化学思维方法,体现了试题的基礎性和综合性。从思维层次看,对M水平和R水平考查的比重较大,对E水平的考查较少,这与新课标Ⅰ卷以综合性较强的试题多维度考查学生综合能力的特点是一致的。E层次的试题要求考生具备很高的综合素养[3],能够体现考试的选拔甄别功能。
2.2 对2018年深圳市高三第二次模拟考试信息型方程式的分析
2.2.1 信息型方程式的分类
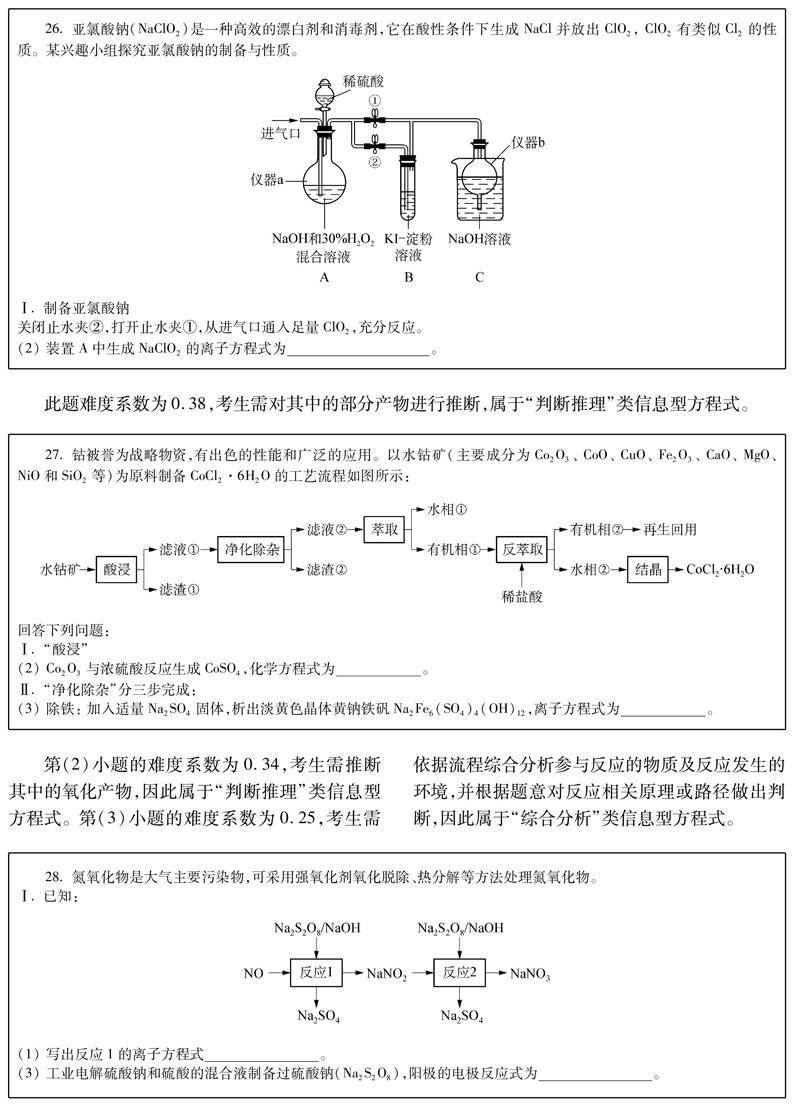
基于上述分类标准,对2018年深圳市高三第二次模拟考试非选择必做题中有关信息型方程式(共5小题)进行归类分析。
第(2)小题的难度系数为0.34,考生需推断其中的氧化产物,因此属于“判断推理”类信息型方程式。第(3)小题的难度系数为0.25,考生需依据流程综合分析参与反应的物质及反应发生的环境,并根据题意对反应相关原理或路径做出判断,因此属于“综合分析”类信息型方程式。
第(1)小题的难度系数为0.54,该小题的物质和环境信息均已给出,属于“直接提取”类信息型方程式。第(3)小题的难度系数为0.47,该小题的物质信息已给出,并指明为阳极环境,属于“直接提取”类信息型方程式。
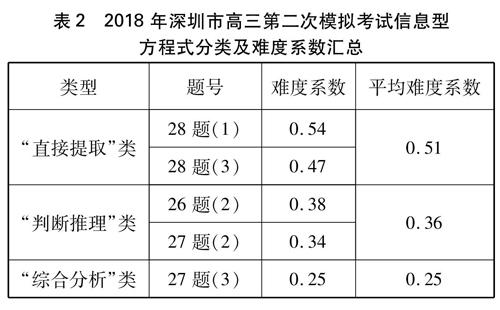
汇总数据可知: 方程式书写中,信息处理方式相同,难度系数也相近,且随所给信息的减少,其相应的难度系数逐渐减小(见表2)。说明方程式书写时需要考生综合推断的思维容量越大,其方程式书写难度就越大,且相应的成绩表现就会越不理想。
2.2.2 三类信息型方程式难度曲线分析
一般来说,全卷得分高的学生,在某道题目上的正答率也应较高。故在考试数据分析中,通常会制作试卷或题目的难度曲线图来直观地反映试题的质量和学生的答题情况。图像中该曲线的理想状态应呈现上升趋势,即对低分段考生而言试题偏难,对高分段考生而言试题较为容易。此次考试的全卷难度曲线(见图1)呈现出了理想的上升趋势,说明此次考试试题整体难度适中,区分度良好。
本文通过计算各个分数段考生在每道信息型方程式书写考题中的难度系数值,并求得同类信息型方程式在相同分数段难度的平均值,得到三类信息型方程式的难度曲线图。
理想情况下,三类信息型方程式的难度曲线与全卷的难度曲线应接近重合,两者之间的区域面积可用于表征两者的偏离程度。由图可知,三类信息型方程式难度曲线图偏离全卷难度曲线的程度从“直接提取”类到“判断推理”类再到“综合分析”类逐渐增大。比较三类信息型方程式难度曲线偏离程度、表2中的平均难度系数以及相应的SOLO思维水平,三者数据呈现出较高的契合度。从曲线整体趋势看,40分以下的考生完成三类信息型方程式均很困难(难度系数不足0.1);对于40分以上的考生群体,三类信息型方程式的掌握情况随总分分数段的提升而愈发良好。
以全卷难度曲线为参考辅助线,若实际曲线上的点偏离辅助线越远,则说明该点对应分数段的学生在学习能力范围内本应得分的题目中失分越严重,相对应的题型在复习过程中应得到重点关注。平行于全卷难度曲线分别作另外三条曲线的切线,切点即为最大偏离点,将该偏离点对应的分数段定义为“最大偏离分数段”。“直接提取”类信息型方程式对应的“最大偏离分数段”为30~39分,这部分学生化学成绩中等偏下,约占全市考生总人数的8%;“判断推理”类信息型方程式对应的“最大偏离分数段”为50~59分,约占全市考生总人数的14%,该学生群体的成绩表现为中等水平;而对于“综合分析”类信息型方程式的书写,总分在60~69的学生群体偏离程度最大,此部分学生为中等偏上水平,约占全市考生总人数的18%。清晰的考生群体分数段划分可以为分层教学提供参考,也为处于不同分数段的学生点明了复习应关注的重点和需突破的难点。
以上数据亦呈现出三类信息型方程式对应的“最大偏离分数段”中的考生人数依次增加,这就说明大部分考生通过二轮复习已经掌握了“直接提取”类信息型方程式的书写方法,其中总分在80分以上的学生群体(约为全市化学学科成绩排名的前19%)已經熟练掌握了此类信息型方程式的书写方法(难度系数大于0.8,超过了全卷的难度系数),故考后应将精力集中于另两类方程式的强化巩固,进一步提炼两类方程式的书写技巧,力求实现质的突破。特别是“综合分析”类信息型方程式,对于分数段为90~100分的学生(约为全市化学成绩排名的前4%),此题的难度系数约为0.8,说明大部分学优生通过有效训练完全能够驾驭此类方程式的书写。
此外,图中“直接提取”类和“判断推理”类曲线出现了交叉。究其原因,试题的难度值随未知物质推断过程的复杂程度、方程式配平的难易程度而波动,且受控于学生对各个不同知识模块的认知水平的差异。
3 思考与建议
3.1 呈现问题链,变式巧训练
信息型方程式的书写往往陌生度高、信息量大,需要学生既具备较强的信息获取、加工和整合能力,又能综合各模块知识、利用有效证据进行推理。因此,复习备考时应在精选习题的基础上,围绕“一题多变”开展变式训练,逐渐合理科学地变换题目所给信息,增大解题的思维容量。教师应基于对学生认知规律的研究,呈现一系列逻辑严密的SOLO问题链,通过简约而高品质的思维层级问题,增强学生思考内容的弹性和灵活度[4],促使学生多维而有序地掌握书写各类信息型方程式的方法,在应用方法的过程中提升不同情境下劣构问题的解决能力。
以“ClO2的制备”为例,设计出以下SOLO问题链,如表3所示。
SOLO问题链的设计,让不同思维水平的学生都能找到适合自己的“最近发展区”,打破了学生凌乱存储知识的状态,使学生感受到知识间丰富的逻辑关系,建立对程序性知识的系统认识。
3.2 分层次设计,进阶式学习
3.2.1 基础为本,体现复习的精度
对于学习程度中等偏下的学生,建议将主要精力集中于“直接提取”类信息型方程式的突破。此类信息型方程式书写失误的主要原因是未能准确从题目中获取有效物质和环境信息,或未能熟练掌握方程式的配平方法。因此,复习时应注重对常见信息来源形式(如流程图、反应装置图等)的总结归纳,不断培养学生获取有效信息的能力;该部分学生还需进一步巩固方程式的配平技巧,提升对信息的加工整合能力,在不断夯实必备知识的同时,逐渐形成清晰的物质观及反应观。总之,对于此类学生,应立足于基础知识和基本能力,通过契合学生认识水平的问题设计,引导学生进行思维聚焦,促使知识理解的模型化,提升复习的精度,让学生学有所获。
3.2.2 能力为先,反映知识的广度
对于学习能力中等及中等偏上的学生,则可重点训练“判断推理”类信息型方程式的书写。该部分学生对方程式的配平技巧驾轻就熟,对于此类信息型方程式的书写,基于证据进行有效推断是关键,正确的推断源于学生对各模块主干知识的熟练掌握,需要学生运用化学学科思想统摄基础知识、基本原理的关联应用。近六年新课标Ⅰ卷中信息型方程式中物质推断的依据如表4所示,此类信息型方程式涉及的知识点众多,而知识的机械记忆对方程式的正确书写并无助益。因此,教学设计应反映知识的广度,融入典型素材,对问题进行阶梯式设计,有效化解学习过程中的思维障碍点,提升学生的高阶思维能力。总之,对于此类学生,应以高阶思维能力的提升为目标,通过丰富的素材、恰当的引导提升知识的广度。
3.2.3 素养为重,彰显思维的深度
学优生已构建了完整的高中化学知识网络体系,并具备一定的综合分析判断能力,能够熟练运用所学知识解决新情境下的陌生问题。对于此类学生,应关注学生的深层思考和深度复习,通过“综合分析”类方程式的书写组织开展预测、设计、解释等高级认知活动,想方设法及时捕捉学生在课堂上展示的认识角度,使学生的认识思路得以外显,偏差认识得到纠正,认识模型在潜移默化中得到构建、巩固和运用[5]。因此,此类方程式的书写有助于彰显思维的深度,有效防止消极思维定势的形成,激发学生的创造性,提升思维品质,发展化学学科核心素养。
致谢: 向对本论文给予悉心指导以及数据支持的深圳市化学教研员吴运来老师表示衷心感谢!
参考文献:
[1]王后雄. 论化学方程式教学中高级知识的形成及教学策略[J]. 化学教育, 2006, 27(1): 12~16.
[2]Biggs J B, Collis K F. Evaluating the Quality of Learning: The SOLO Taxonomy (Structure of the Observed Learning Outcome)[M]. New York: Academic Press, 1982.
[3]申燕, 謝新民, 解慕宗. 基于SOLO分类理论的思维层次与学生成绩相关度研究——以2017年深圳市“四校联考”为例[J]. 化学教学, 2018, (8): 25~28.
[4]刘志华, 谢洁纯. SOLO指导下思维导图式教学设计的研究[J]. 化学教学, 2018, (7): 40~45.
[5]黄素雯. 例谈有机合成认识模型在单元复习中的应用[J]. 化学教学, 2018, (8): 77~81.
