输油管道铺设的优化模型
2019-07-02廖淑华
李 静,廖淑华,乔 铁
(郑州铁路职业技术学院,河南 郑州 451460)
管道是石油工业的动脉,是石油生产中的重要环节。如何合理设计管道的铺设线路以减少建设费用的问题,已受到人们的重视。某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个车站,用来运送成品油。由于这种模式具有一定的普遍性,油田设计院希望建立管线建设费用最省的一般数学模型与方法。本研究根据2010年全国大学生数学建模竞赛专科组的C题(简称竞赛题),建立输油管道铺设的优化模型。
1 问题的提出与分析
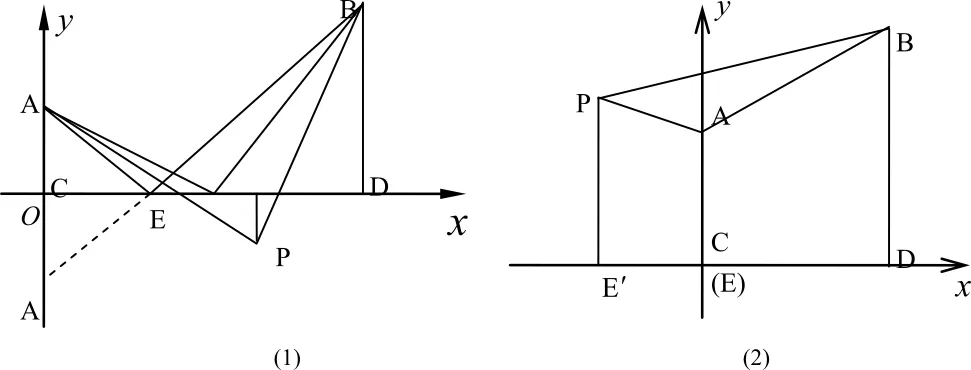
对于竞赛题中的问题(1),可以看作是共用管线与非共用管线费用是否相同两种不同情形。在这两种情形中考虑两炼油厂到铁路线的距离和两炼油厂间距离的各种不同情况,设计出使管线建设费用最省的方案。经过分析得出了以下几种可能的炼油厂位置,如图1所示。
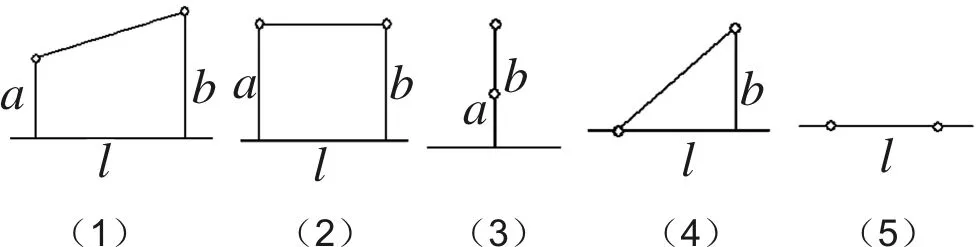
图1 两个炼油厂与铁路线可能的位置示意图
图1(1)表示两炼油厂连线不与铁路线平行的情况;图1(2)表示两炼油厂连线与铁路线平行的情况;图1(3)表示两炼油厂连线与铁路线垂直的情况;图1(4)表示一个炼油厂位于铁路线边缘的情况;图1(5)表示两炼油厂都位于铁路线边缘的情况。
根据实际资料可知,炼油厂与铁路线距离过近(a,b<80m)时发生火灾等灾害的可能性大,从安全方面考虑,图1(4)和图1(5)所示的两种情形不符合实际,故不考虑。对图1(1)所示情形进行分析求解,可以得到一般的模型(注意考虑共用管线与非共用管线费用相同与不同的两种情形)。
当共用管线与非共用管线费用相同时,欲使管线建设费用最省,只要使总线路最短即可。由勾股定理即可得线路总长。
当共用管线与非共用管线费用不同时,若共用管线与非共用管线费用之比为k:1,欲使管线建设费用最省,只需满足共用管线加权后,总线路最短即可。但是,当k≥2时,使用共用管线输油会比全部使用非共用管线输油的费用多,因此只需考虑1≤k≤2的情形,其余思路、算法同上一种情形。
竞赛题中的问题(2)在问题(1)的基础上,给定一些参数,要求设计出最优方案、计算出最小费用。首先根据所给的附加费估计表,对各公司的资质等级采用1-9比较原则建立比较矩阵,计算出各公司在评估附加费时的权值,即可得到在城区铺设管线所追加的附加费为21.4万元/km。然后,分别计算出铺设在城区的管线长度和铺设在郊区的管线长度,得出总铺设长度。最后,根据各自的费用以及在城区铺设管线所追加的附加费用,建立总费用函数。利用MATLAB软件求解出共用管线与非共用管线交汇点的坐标,以及城乡管线交汇点坐标,从而得到最优方案,并求出费用的最小值。
竞赛题中的问题(3)是在问题(2)的前提下,进一步强化了条件,根据各炼油厂输油能力,视情况挑选管线材质,进一步节省了管线材质的开销,使得费用尽量减少。由于各炼油厂输油管线材质不同,价钱也不同,因此对于不同的城乡管线以及炼油厂输油管赋予不同的加权值,建立总费用函数。利用MATLAB软件求解出共用管线与非共用管线交汇点坐标,以及城乡管线交汇点坐标,从而得到最优设计方案,并求出费用的最小值。
2 竞赛题问题(1)的模型建立与求解
对于特殊情形l=0时,即两炼油厂连线垂直于铁路线,如图2所示,最优方案是车站设在E点处。
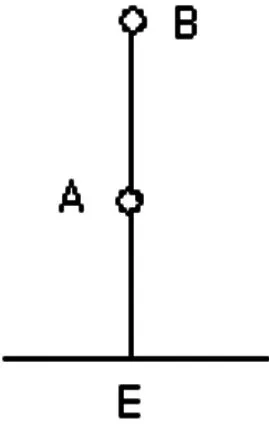
图2 两厂与车站的位置
以下在l>0的情形下讨论。
在不确定有无共用管线的情况下,可先给出一种一般的情况进行分析计算。在此情况下,讨论共用管线与非共用管线费用相同与不同的两种情形。
1)共用管线与非共用管线费用相同
要使费用最省,只要管线铺设长度最短即可。如图3所示,建立直角坐标系,设管线交汇点为P(x,y)。根据勾股定理,可以得到共用管线与非共用管线费用相同时所铺设管线总长度为
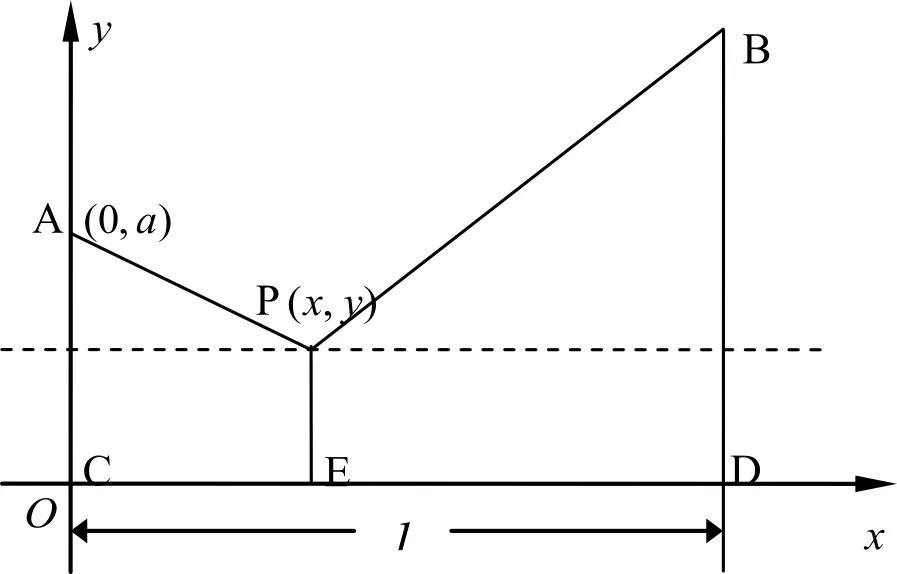
图3 共用与非共用管线费用相同的情况
利用MATLAB软件求解得
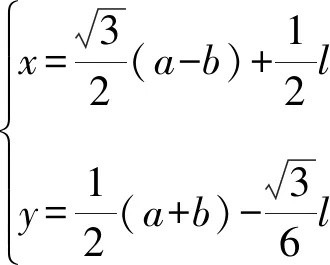
容易验证,问题的最优解为
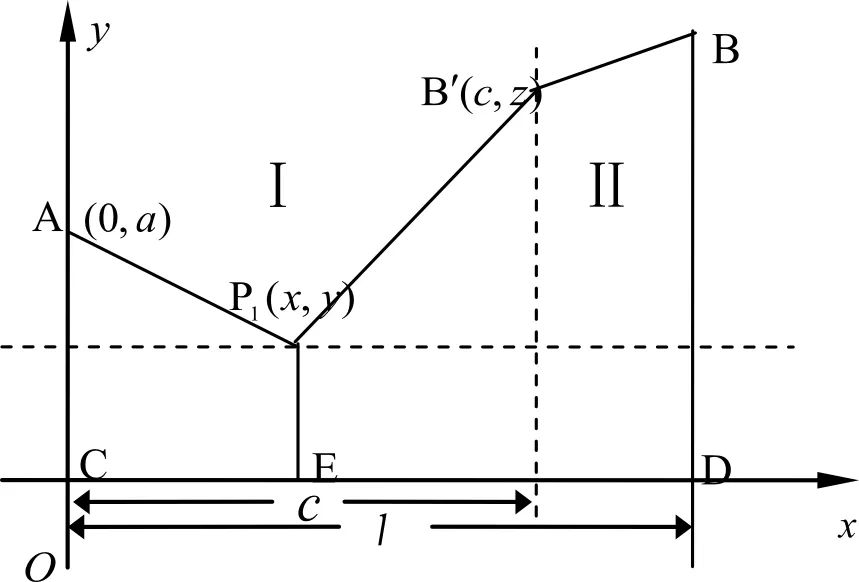
根据实际情况,不妨设a 图4 两厂和车站设置示意图 2)共用管线与非共用管线费用不同 对于共用管线与非共用管线铺设费用不同的情况,可设共用管线费用与非共用管线费用之比为k:1,且k>1。在共用管线与非共用管线费用相同的基础上,给共用管线加一个权值,便可得到总铺设长度为 利用MATLAB软件求解得到最优解为 当1 由于问题(2)要考虑管线铺设在两种不同的区域,即城区和郊区。在城区管道铺设时,还要考虑支付拆迁等附加费的情况,为估算此项费用,特聘请了三家工程咨询公司(其中公司一具有甲级资质,公司二和公司三具有乙级资质)进行了估算。这三家公司估算出附加费用分别为21万元/km,24万元/km,20万元/km。 由于三家公司所给出附加费用不同,而且其资质等级也不同,可以将三家公司所提供的拆迁等附加费的估算情况和公司资质等级进行一个系统、全面的综合分析。这里采取1-9比例标度方法,得到各公司在评估附加费用时所占权重。 由于铺设管线每千米的拆迁等附加费用是铺设管线费用的近三倍之多,因此在确定设置方案时要尽量减少在城区铺设管道的长度。根据分析结果,做出管线铺设的方案如图5所示,不妨设城乡管线交汇点B′的坐标为(15,z)。 图5 城乡共用铺设管线的示意图 根据勾股定理得到在城乡共同铺设管线所需总费用函数为 利用MATLAB软件求解可得x=5.451 3,y=1.852 7,z=7.365 6,最小费用值为w1=282.193 4(万元)。 考虑问题(3)的方法与问题(2)类似。但是由于两炼油厂的产油能力不同,在铺设非共用管线时,则可采用不同材质的管线,即各炼油厂非共用管线重要性程度不同,可以赋予不同的权值,从而可以减少管线的投资费用。 由于在城区铺设管线的附加费用21.4万元/km不变,因此,要尽量减少在城区铺设管线的长度。 设计方案如图5所示。设城乡管线交汇点坐标仍记为(15,z),由勾股定理可得到在城乡共同铺设管线所需要的总费用函数为 利用MATLAB软件求其最小值,得x=6.735 5,y=0.137 7,z=7.276 8,其最小费用值为w2=251.463 3万元。 (1)在竞赛题问题(2)中,采用1-9比例标度计算得出附加费用为21.4万元/km。如果使用算术平均值计算出的附加费用为21.67万元/km,则二者相比差别不大,因此方法是合理的。 (2)在竞赛题问题(2)和问题(3)中,关于z的取值比较接近8。这也就是说城郊结合点选在B点处,是在城市和郊区的交汇界线的垂足点偏下一些,与实际情况是相符合的。 (3)在竞赛题问题(2)中,在选择三家咨询公司的权值时,并不一定要采用1-9比例标度方法,也可以考虑其他合适的权值。譬如可以对两种极端情形1:0:0和1:1:1做进一步分析,给出附加费用的范围,从而也可以得到最小费用的一个范围。 (4)虽然该模型是根据输油管线铺设问题给出的,但模型也可以直接应用于综合布线问题和天然气等其他管线的铺设问题。 (5)该模型能够较全面反映问题中所给的各项条件对问题的影响,根据要求建立相应的数学模型。运用数学软件和方法求得最优解,选择出最优的输油管线设计方案,使得铺设管线的费用最省。该模型适用范围广泛,能求解多类管道铺设问题,亦能用于优化公路线路设计问题,稍加改进也可运用于运输领域。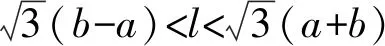
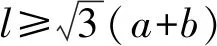
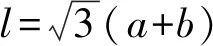
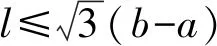
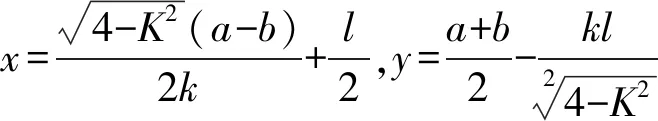
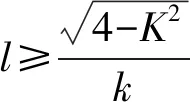
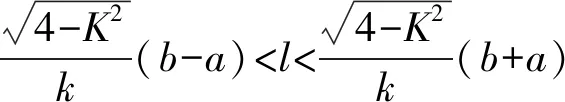
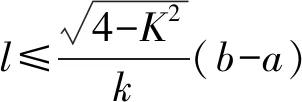
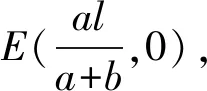
3 竞赛题问题(2)的模型建立与求解
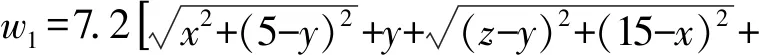
4 竞赛题问题(3)的模型建立与求解
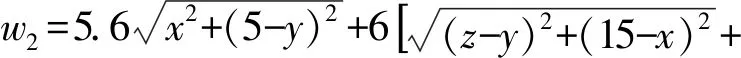
5 模型的结果分析与评价
