基于蚁群算法的土石方调配优化

2019-07-02黄丙湖郑俊秋徐帮树

土木工程与管理学报 2019年3期

黄丙湖，赵芸，吕瑞，郑俊秋，徐帮树

(1. 中国石油大学(华东) 地球科学与技术学院，山东青岛 266580；2. 山东大学齐鲁交通学院，山东济南 250002)

十八大以来，我国新型城镇化发展迅速，十九大报告中为推进新型城镇化指明了方向，提出“以城市群为主体构建大中小城市和小城镇协调发展的城镇格局”[1]，而在城市群推进过程中，无论是建设交通运输网、还是构建完备配套的基础设施体系，都与建筑工程密切相关，给建筑企业带来了巨大的市场空间。而成本是影响工程施工的最基本因素之一，在施工过程中如何科学节约成本、缩短工期一直是项目考虑的焦点。因为，项目施工成本的金额是巨大的，常常达到千万甚至过亿。土石方调配作为建筑施工项目的一个重要方面，指的是在项目施工中，依据施工地势设计的要求，科学地进行开挖、运输、填筑、借料、弃废料等环节所组成的综合系统[2]。然而，调配过程依赖昂贵的施工设备，这些设备既要操作也要维护，在大型工程建设，尤其是大型水利工程和机场工程中，土石方调配费用占工程预算的比重很大。因此，优秀的土石方调配方案可以节约施工成本、缩短施工工期，具有较好的经济效益[2]。

国内外学者在土石方调配问题的研究上取得了丰富的研究成果，包括各种调配模型和求解模型的优化方法。在国外，Moreb[3]将道路坡度作为决策变量来优化土石方调配；Mohamed Karimi等[4]考虑道路工程土石方调配过程中的不确定性，建立了模糊线性规划调配模型。在国内，袁建丰[5]将线性规划法应用于三峡工程右岸的土方工程，得到基于线性规划的最优土石方调配方案；於永和等[6]分析了堤防工程中的土石方调配问题，并建立了调配模型；邓朗妮[7]等验证了基于线性规划模型优化土石方调配问题的可行性。这些研究工作对实际调配系统存在的非线性关系做了近似线性化，虽然发挥了线性规划模型建模简便、易于计算的优势，但忽视了实际工程中存在的非线性因子，建立经济可行的调配方案的能力有限。

针对线性规划法的缺点，许多学者开始在土石方调配中引入进化算法、蚁群算法和粒子群算法等可以考虑非线性因素的智能优化方法。Henderson[8]提出了基于模拟退火算法土石方调配模型，来寻找填挖方之间的最短运距；王仁超等[9]提出了一种基于蚁群粒子群混合优化算法的土石方优化调配方法；陈秀铜[10]等分析了土方调配中的非线性约束的特点，将改进的粒子群算法应用于工程实例中，并验证了此方法的可行性。这些研究可以考虑调配中的非线性因素，但是忽略了调配过程中施工设备的施工次序问题，在建立经济可行的调配方案的能力上是有限的。

因此，本文提出一种可以考虑施工次序的土石方调配优化模型，主要目标是找到一个使填挖方之间平衡的总成本最小的施工次序及运输量。由于蚁群算法可以考虑非线性约束，在求解离散问题上优势明显，本文采用蚁群算法求解优化模型，并且针对传统调配表存在的可读性较差的缺点，将调配解决方案绘制成一个详细的矢量指导图，这种可视化表达很容易理解，可以减少不必要的通信及施工差错。

1 土石方调配优化模型构建与求解

建筑工程常常需要修整场地的地形地势，具体来说，需要从高于设计标高的土方位置开挖土方，并将其运输到低于设计标高的土方位置。而运输依赖施工车辆，这些车辆既要操作也要维护，因此规划者需要制定一种土石方调配策略，以减少在填方和挖方地点之间移动的车辆的成本，达到减少项目整体成本的目的。

土石方调配是对地形地势的改造，对于地理信息科学而言，土石方可以看作地表地物，它蕴含着丰富地理信息，如坐标值、高程、坡度等。土石方的这些地理特性使得调配过程可以看作由结点和弧段组成的图结构，结点包含土石方开挖对象、填筑对象、废料场和借料场，弧段则是结点间的土石方运输路径。

1.1 模型建立

为了构建土石方调配优化模型，需要做几个定义。假设有N个调配相关结点，是挖方区、填方区、借料区和弃料区构成的集合，定义为L={1,2,…,N}；调配成本由成本矩阵C来表达：

(1)

cij=f(dij,i,j)，∀j∈{1,2,…,N}

(2)

式中：cij为i,j结点的单位土方调配成本，主要包括运输成本，它与结点间的距离dij相关，但结点间的运输成本不一定是与运输距离线性相关的，它还与滚动阻力、坡度、燃料及设备的维护等相关联。而且调配成本不仅仅是设备运输的成本，它还包括填筑成本、开挖成本、借弃料场的存储费用等[11]。

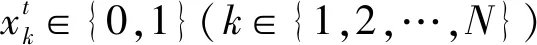
在这个模型中，步骤数即为施工次序，建立的优化模型的目标函数为：

(3)

式中：Et为第t步运输的土方量；ct为第t步施工相关的单位土方量的成本，定义为：

ct=XCXT

(4)

优化模型需要遵守各种约束条件，首先要保证每一步施工仅有一个起始结点，则有：

(5)

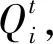
(6)

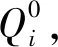
(7)

(8)

随着施工次序的推进，填方结点的剩余土方量(可以看作亏损量)增加，挖方结点的剩余土方量减少，最终经过S步的施工后，各结点的土石方剩余量要达到设计的最终土方剩余量Ri：

(9)

由于调配结点分成填、挖两类，因此需要对第t步的运输量Et进行约束，若起始结点是填方结点，第t步是空车运输；若是挖方结点，第t步是载重运输，且运输的土方量不能超过挖方结点剩余的土方量：

(10)

(11)

1.2 模型求解

本文提出的模型与旅行商问题(Traveling Salesman Problem，TSP)类似，都是要寻找一条最优路径，使成本减少到最低。旅行商问题可形容为寻求旅行商从某个城市出发,访问每个城市仅一次，最后回到出发点的最小路径成本[12]。与旅行商问题不同的是此模型所求的土石方调配路径不用构成哈密顿回路，即每个城市可以访问多次并且最终不用回到出发点。

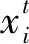
基本蚁群算法是Marco Dorigo等人受蚁群在寻找食物过程中表现出的高度的协作性的启发，提出的一种模型化蚂蚁行为的智能优化算法[13]。

它是一种概率型算法，在路径搜索过程中，依照概率选择访问的下一地点，设蚂蚁k由地点i进行搜索，则它转移到地点j的概率为：

(12)

式中：τ(i,j)为蚂蚁在i，j间释放的信息素；η(i,j)为ij上的启发信息；W为蚂蚁k未访问地点的集合；α，β为τ(i,j)，η(i,j)的相对权重系数。在本模型中，启发信息选取每一步施工成本的倒数：

(13)

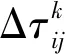
τij(mt+1)=(1-ρ)τij(mt)+Δτ(i,j),0<ρ<1

(14)

(15)

(16)

本文构建的模型具有复杂约束条件，基本蚁群算法在求解约束条件复杂的问题时，因其搜索的随机性可能造成搜索空间扩大，甚至构造出不可行解，会增加算法的搜索时间。为了保证模型的求解质量和效率，采用动态优先集策略改进基本蚁群算法，根据约束条件和地点信息确定地点的访问优先级，以减少算法生成的不可行解。结合土石方调配的改进蚁群算法的方法步骤[14]如下：

(1)初始化蚁群参数和土石方结点的属性信息。设置最大迭代次数MaxDT、启发因子和信息素蒸发系数等参数，令迭代次数mt=1，输入结点i的地理位置信息和起始土石方量Si。

(2)将m只蚂蚁随机放在n个城市里。每只蚂蚁完成的一次路径搜索都是土石方调配问题的一个解决方案，逐步确定土石方调配成本和施工次序。这n个城市是挖方结点的子集，n∈{L+}，也就是说，每只蚂蚁的起始位置是挖方结点。

(3)进入迭代，蚂蚁的索引号k=1。

(4)循环执行下列步骤：1)确定蚂蚁下一步访问的候选集。设当前执行的施工次序(步骤)为t，如果当前结点i是挖方结点，则下一步访问填方结点的优先级要高于挖方结点，如果是填方结点，则挖方结点的优先级高于填方结点。2)根据状态转移公式(12)确定访问的下一点。确定i到上一步侯选集合中各个结点的土方运输量，以计算转移概率，随机选择具有较大概率的结点作为访问的下一结点j。3)更新相关结点I，j的土石方剩余量。4)若各个结点的土方剩余量均达到设计的土方量，则完成该蚂蚁个体的路径搜寻，执行第(5)步。否则以结点j为出发点重复1)～3)步。

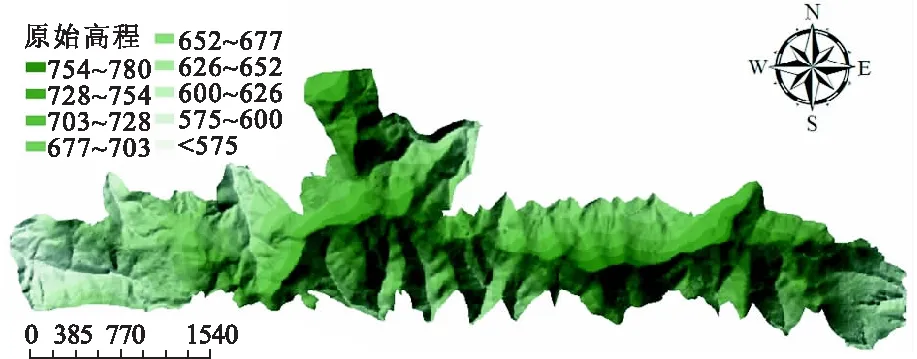
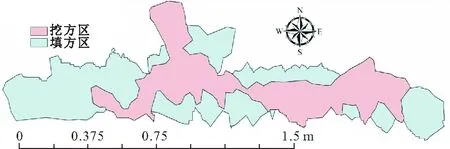
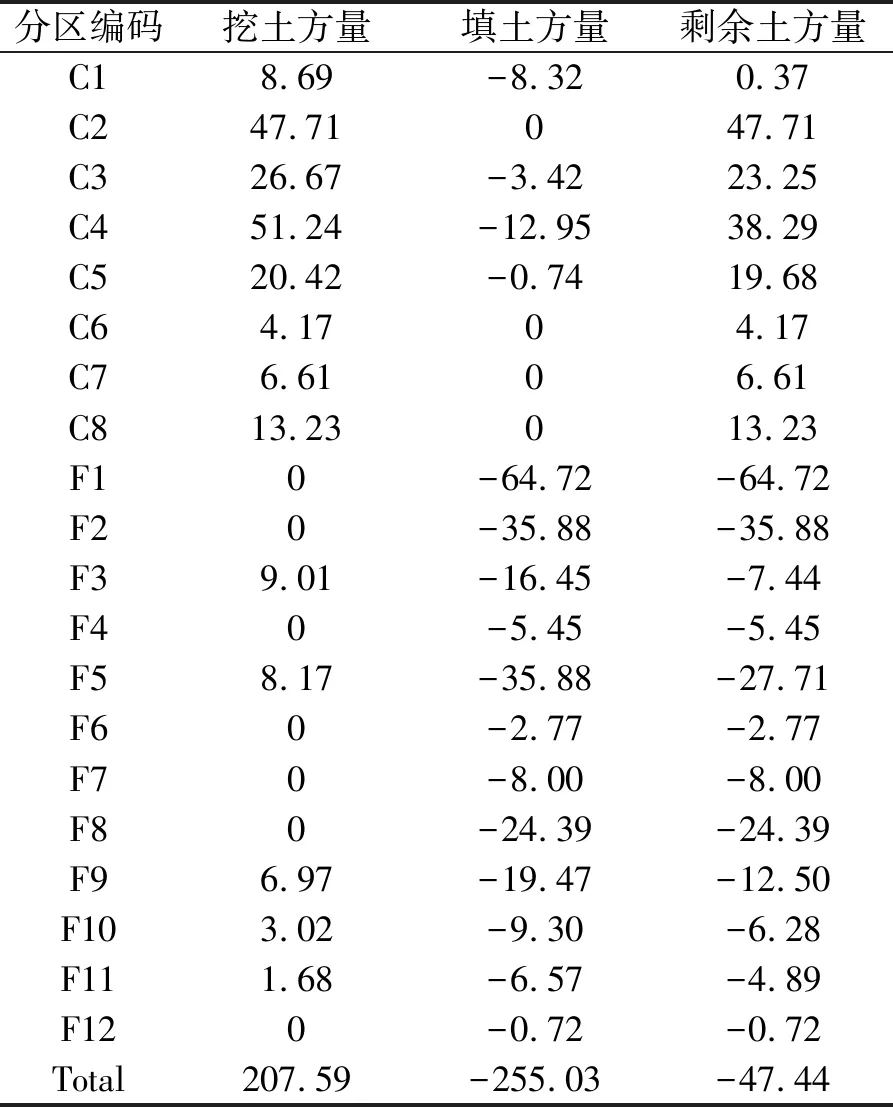
(5)如果k

(6)记录本次迭代的最佳路线，更新信息素。

(7)如果迭代次数超过MaxDT，则跳出迭代输出调配成本最优值和调配方案，包含施工次序，否则跳转至第(3)步。

2 实例应用

A项目占地231 ha，土石方填挖总方量5100600 m3，最大填方高度112 m，地形复杂，需要削两峰填一壑，工程量大，考虑整个工程的土石方填挖平衡，需要向借料场借土474400 m3，根据项目的特点，调配距离长，考虑施工次序就显得格外重要。

为了清楚地理解调配方案，也为了建模简便，对施工场地分区，划分成二维规则格网单元，将格网中心点抽象成模型的调配结点，这样每个格网都能匹配唯一x-y坐标值，即编码，借料场也用同样的方式来表示。各分区土方量的计算借助具有强大的空间分析功能的地理信息系统方面的专业软件ArcGIS来实现。首先，利用ArcGIS软件提取出dwg格式的项目地势设计图和原始地势图包含的地理信息，拟合得到地面高程以及填挖方总体分布情况，如图1～3所示。紧接着，根据DEM (Digital Elevation Model)法[15]原理计算各分区土方量，这种拟合方法并不强求测点高程值为函数值[16]，各个结点的土方量详情如表1所示。由表1可知，本项目场区内的土石方量难以平衡，计算得到场区内的总填方量2550300 m3，挖方量2075900 m3，是不能场地内平衡的，需要向借料场借土。

图1 施工场地原始地势/m

图2 施工场地设计地势/m

图3 填挖方分布总体情况

×105 m3

模型求解还需要各个结点间的距离，本例里使用结点间的直线距离，这导致模型得到的解为近似值，但如果已知结点间道路实际距离，直接替换计算即可，模型不需要进行修改。设土方的成本单价为1元/(m3·km)，利用第一部分建立的优化模型以及第二部分的蚁群算法求解可以得到A项目的最优调配方案结果，表2为蚁群方法计算的填挖方调配数据，从表2中可以得到各挖方区调配到填方区的土方量，但是施工次序模糊，可读性较差。

由于本文模型考虑了施工次序，所以可以将调配结果通过矢量图的形式展示，如图4所示。施工起点位置标记五角星，施工终止点标记多角星；实线表示载重运输，虚线表示空车运输(运输量为0)；序号表示当前施工次序，并标注当前次序运输的土方量。这样，增强了土石方调配过程的可读性，既从全局角度把握整体布局，又从局部角度把握各分区的具体施工情况。

表2 蚁群方法计算的填挖方调配数据 ×105 m3

图4 土石方调配矢量指导图/×105 m3

为了证明本文方法的可行性，设每土方单位的成本单价为1元/(m3·km)，再次利用线性规划法和基本蚁群算法对本项目的土石方调配问题进行求解，线性规划法得到的最小成本为4.441百万元，其计算结果如表3所示。因不考虑施工次序，所以无法使用矢量图直观表示；基本蚁群算法得到的最小成本为457.8 万元；而利用本文方法得到的最小成本为445.7 万元。两种蚁群算法的适应度进化曲线如图5所示。由图5可知算法的迭代次数为7000 次，改进后的蚁群算法在迭代到4615次时得到全局最优解。由表4可知，一方面，与线性规划法相比，蚁群算法在考虑非线性因素、施工次序、表达方式方面优势明显，同时还可以一次性获取若干次优调配方案。另一方面，基本蚁群算法的最小成本相对误差约为2.85%，运行时间为415.4 s，运行效率不高。而与基本蚁群算法相比，本文改进的蚁群算法求取的最小成本更接近线性规划法求得的最优成本，相对误差约为1.13%，运行时间缩短了约102 s，提高了运行效率。