土钉-桩锚支护体系中土压力与m值对桩身水平位移的影响

2019-07-02王逸波顾晨霞

土木工程与管理学报 2019年3期

吴炎，王逸波，顾晨霞，胡坤

(1. 常州大学怀德学院，江苏靖江 214500； 2. 常州大学环境与安全工程学院，江苏常州 213164)

在城市基坑工程施工中，市政道路、管线和高层建筑物大多分布在基坑周围，环境复杂，施工条件恶劣[1～3]，而这些建筑物又对基坑支护结构和周围土体的变形有严格要求[4,5]。

随着设计和施工水平的发展，深大基坑也由单一的支护体系向复合支护体系过度，土钉墙支护与桩锚支护在我国运用较为普遍[6]，将两者相结合的土钉-桩锚支护对深基坑具有很强的适用性[7]，相关研究表明，采用土钉墙加桩锚的支护方式在牺牲一部分临场用地的基础上能显著降低工程造价[8]。

而最新的《基坑工程支护规程》中，对土压力的计算依旧采用朗肯土压力，而土体在变形过程中，往往都未达到极限状态，实际土压力大于主动压力[9]，同时，采用弹性地基梁法计算桩体变形时[10]，m值的选取也不是单一的，工程地质规范和经验公式给出的值两者并不一样，这就给设计人员带来一定困扰[11,12]。

在前人的研究中，基坑变形过程中土压力的研究较多，但是对于其变化与m值结合对桩体变形的影响则较少。本文对土钉-桩锚支护中桩锚支护段采用不同土压力计算模型与不同“m”值进行桩体变形计算，给出桩体内力变化与桩体水平变形特征，并将桩体计算结果与模拟值和监测值进行对比，提出相应建议。

1 工程概况

1.1 工程简介

本场地位于常州市龙城大道、晋陵中路路口，北侧为龙城大道，西侧为惠山南路，南侧为锦绣路，东侧为晋陵中路。基坑形状不规则，基坑面积约134000 m2，周长约1550 m。基坑大范围开挖深度约12.35～14.00 m(局部地下一层开挖深度约9.80 m)。

1.2 周边环境

本工程周边环境复杂。基坑施工环境保护主要敏感目标为路面，以及路面以下的通信线、给水管、燃气管以及煤气管线等，对于建筑物的影响主要是地铁车站风井、雨水泵房的基础和住宅小区，因此对于周边环境的沉降以及建筑物的倾斜监测非常重要。

1.3 土层条件

基坑土层参数指标如表1。

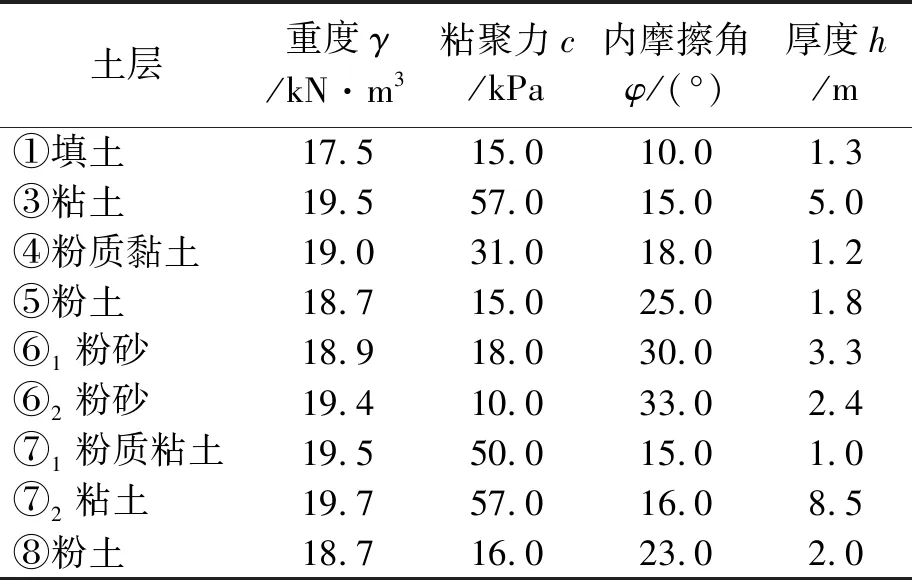
表1 基坑土层

1.4 围护设计

基坑主要采用上部自然放坡(土钉墙)+下部桩锚的支护体系。桩锚支护主要是钻孔灌注桩+三轴搅拌桩(止水帷幕)+高压旋喷锚索的支护型式，桩间采用喷浆保护处理。

基坑坑内采用井管疏干降水+明沟集水井的排水方式，基坑外(止水帷幕外)主要采用管井降水(降低第一承压水水位)的降水方式，基坑北侧为二级放坡+止水帷幕的围护型式。图1为基坑土钉-桩锚支护的形式。

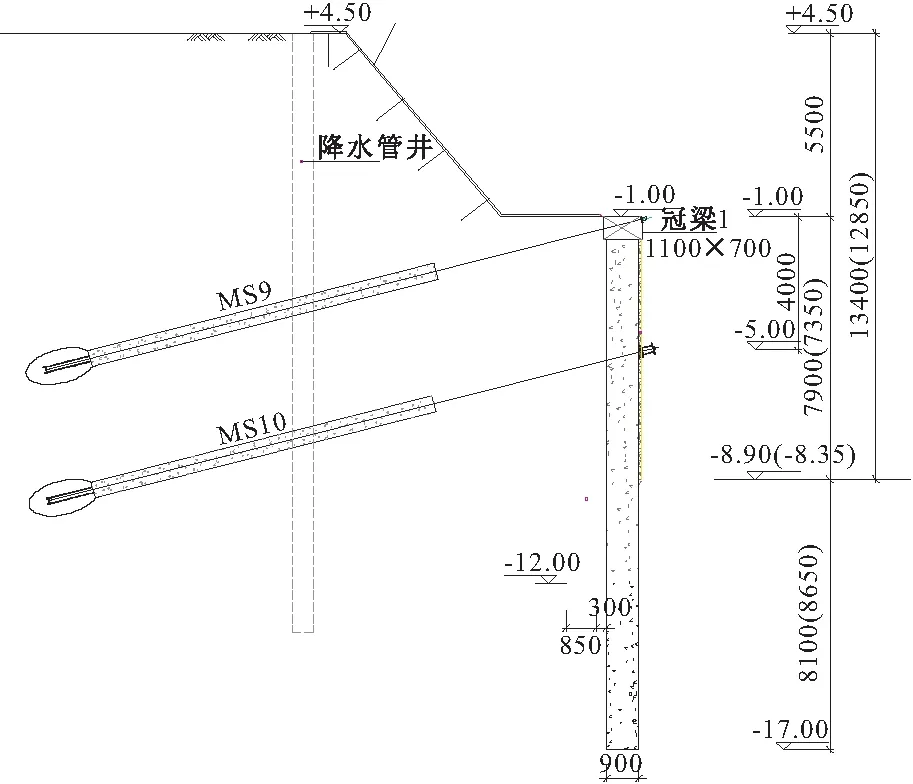
图1 支护结构剖面/mm

其工况划分如表2：

表2 工况划分

2 理论计算

以弹性地基梁法为基础，结合黄强推导的适合手算的公式和参数进行计算，同时，针对土压力采用不同的计算模型，由于不同方法计算的拼写较长，所以简写如下：

A方法：朗肯土压力下选用工程地质规范的m值进行计算；

B方法：线性法土压力下选用工程地质规范的m值进行计算；

C方法：朗肯土压力下选用经验公式求出的m值进行计算；

D方法：线性法土压力下选用经验公式求出的m值进行计算。

图2为工况五桩身弯矩图，从图中可以看出，采用线性法计算的桩身弯矩最大值是采用朗肯土压力法计算的2倍多。在相同情况下，不同m值对桩身弯矩的影响较小，两者的差值小于10%，在不同工况下，线性法土压力下选用工程地质规范的m值进行计算的桩身弯矩值最大。在坑底以上，无论是正弯矩还是负弯矩，其最大值往往小于坑底的最大值。

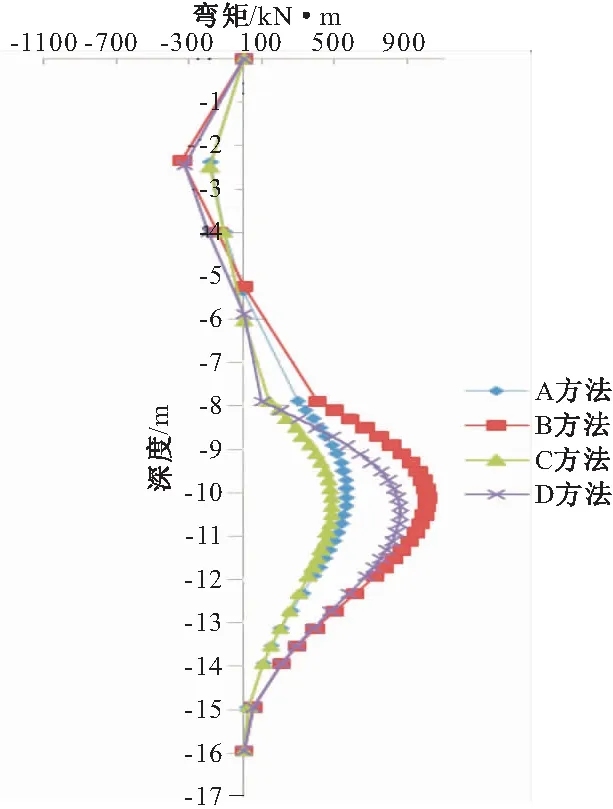
图2 工况五桩身弯矩

图3为工况五桩身剪力图，从图中可以看出，在工况五时，线性法土压力下选用工程地质规范的m值求出的最大剪力大小达到了极大值，为450 kN。采用线性法土压力计算出的最大剪力值大小在同一深度处皆大于采用朗肯土压力的情况。与弯矩情况类似，在相同的情况下，不同m值对桩身剪力的影响较小，土压力的计算方法对剪力的变化起着主导作用。

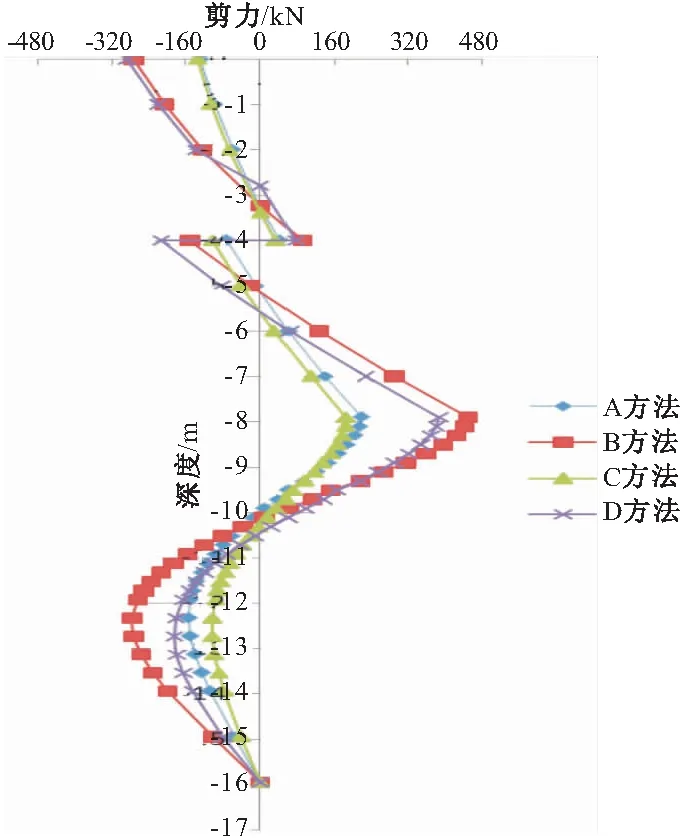
图3 工况五桩身剪力

由于锚索的存在，剪力往往在达到极大值时会产生突变，因此，锚索对桩身的剪力有着很好的约束作用[13]。不同工况下坑底水平位移如图4所示：

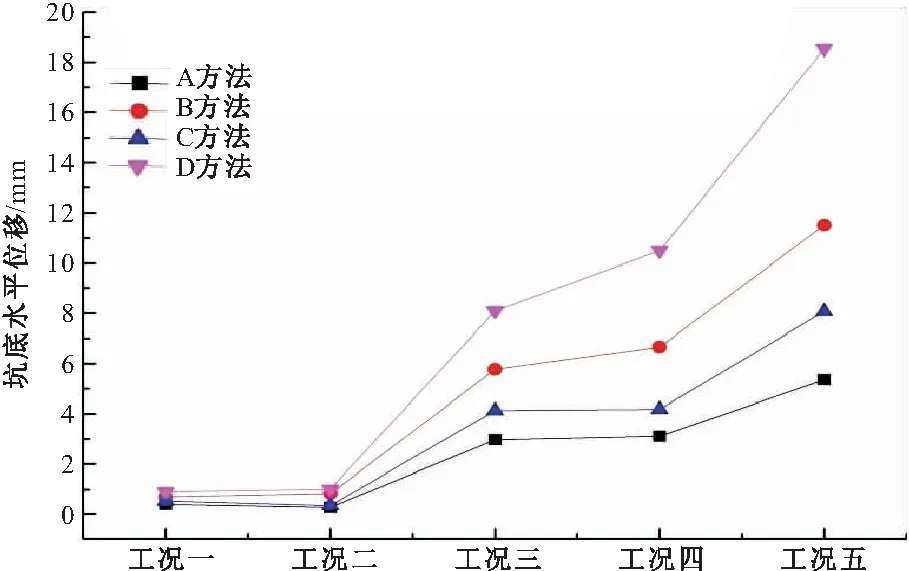
图4 不同工况下坑底水平位移

从图中可以看出，随着工况的渐进，即随着开挖的增加，坑底水平位移总体呈上升趋势。然而，在工况二时，朗肯土压力下求出的坑底位移会有小幅度下降，其范围约0.2 mm，这是工况二支锚的缘故，在工况一到工况二土压力不变的情况下，锚索会使得土体产生向坑外的位移。但是，在工况四时，即支第二根锚索时，四种情况下，坑顶位移都是在增加的，即根据图4发现，此时，锚索内力重分布，但水平位移增加的量也非常小，最大为2.3 mm，最小只有0.05 mm。

在四种情况下，线性法土压力下选用经验公式求出的m值计算出的坑底位移最大，且在开挖到7.9 m时，坑底位移达到最大，有18.537 mm，而朗肯土压力下选用工程地质规范的m值求出的坑底位移最小，在开挖7.9 m时的坑底位移仅有5.345 mm，其他两种情况介于这两者之间。

桩顶位移在基坑工程中有更为直观的体现，不同工况下桩顶位移如图5所示：

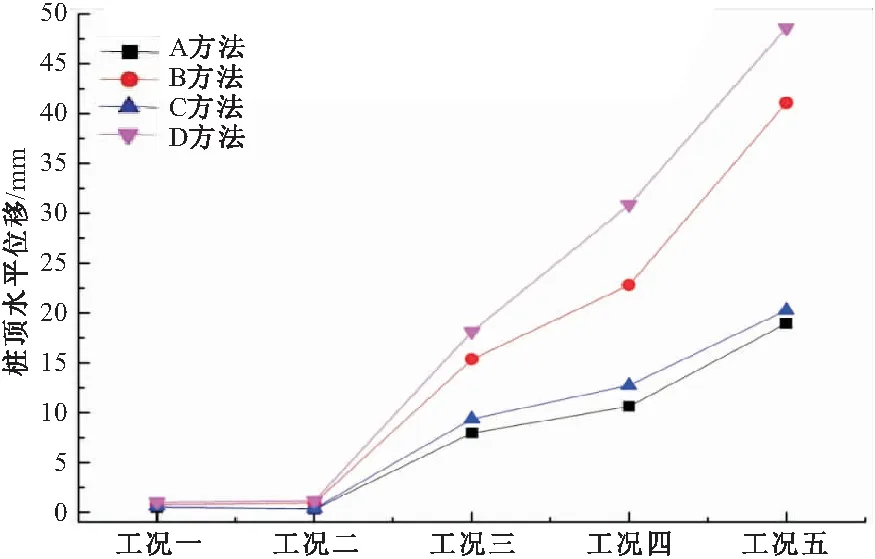
图5 不同工况下桩顶水平位移

如图5所示，桩顶水平位移的变化趋势与坑底水平位移的趋势相同。但与之相比，由于基坑上部锚索的影响，朗肯土压力下求出的坑顶位移与线性法土压力下求出的位移相差较大，幅度最大为58.68%，最小为43.06%。而在相同计算土压力的情况下，m值对桩顶位移的影响较小，变化幅度最大为26.05%，最小为6.54%，且最大值出现在线性土压力模式下，最小值出现在朗肯土压力模式下。

3 监测方案

该地块自2015年9月中旬开始进场进行监测点布设及初始值采集，9月24日工程桩及基坑围护桩开始施工，至2016年7月初一期基坑(东、南、西三侧)回填完毕，一期现场监测工作全面结束。监测点的布设见图6。本工程累计监测历时约9个月，其中监测工作阶段大致划分如下：

(1)第一阶段(2015年9月15日～2015年10月13日)：工程桩、基坑围护桩施工及坑内疏干降水施工。

(2)第二阶段(2015年10月14日～2016年1月24日)：土方开挖施工。本阶段自2015年10月14日土方开挖开始起，至2015年12月31日基坑土方基本开挖完成，直至2016年1月24日基础大底板全部浇筑完成(东侧斜撑区域后做)。

(3)第三阶段(2016年1月25日～2016年7月05日)：地下结构施工。本阶段基坑底板养护达到一定强度后，施工地下结构，至2016年4月上旬开始回填，直至2016年7月回填完毕。

图6 监测点布置

4 桩身水平位移的计算值、监测值以及模拟值对比分析

将监测数据结合理论计算的桩身水平位移，两者进行对比分析，如图7所示。

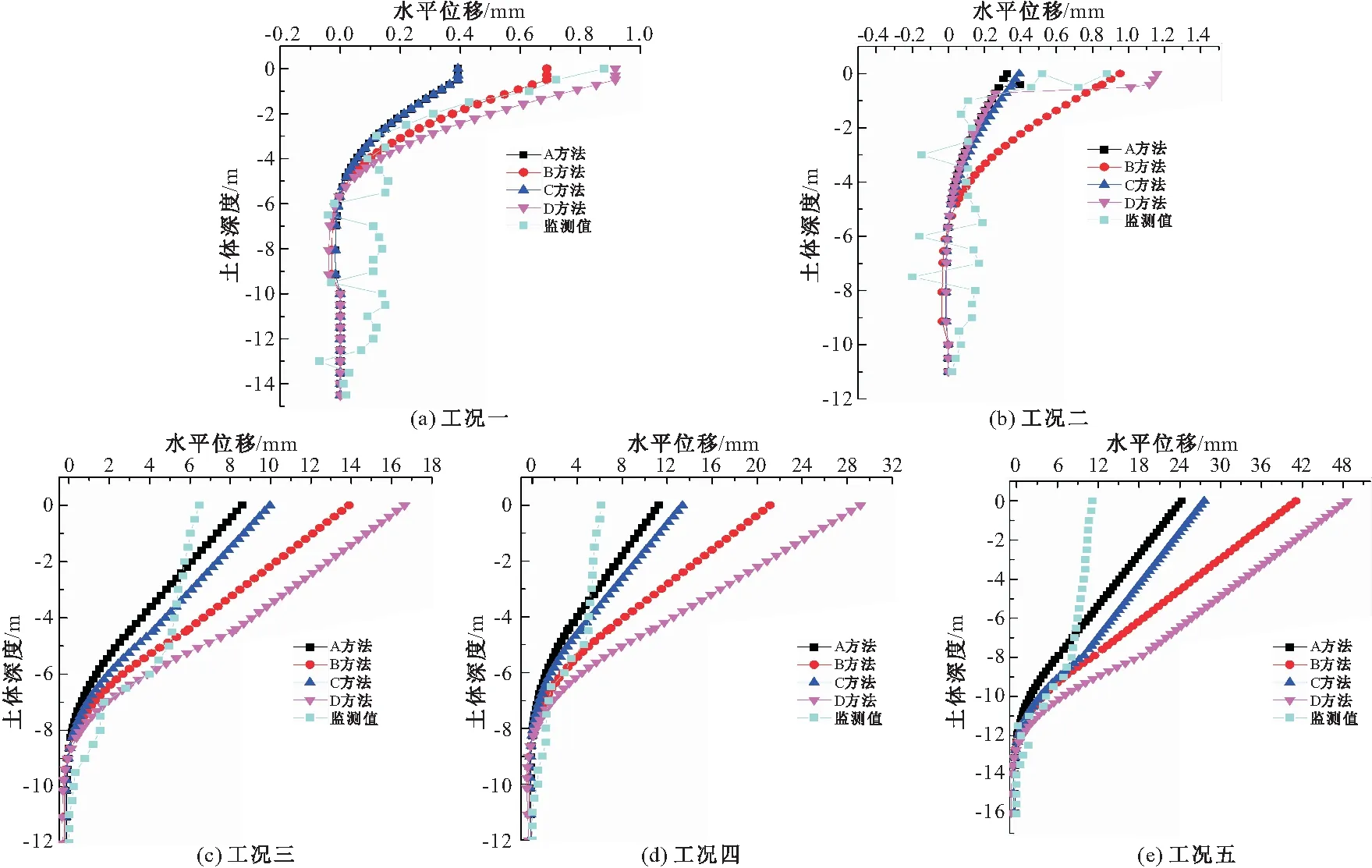
图7 计算位移与监测水平位移对比

从图7可以看出，工况一和工况二，无论哪种方法计算桩身位移，其与监测的水平位移差距都比较小，范围在1 mm以内，这也与开挖深度较浅有关。随着开挖深度的加深，在工况三与工况四时，朗肯土压力下计算的坑底水平位移小于监测值，其相差范围在37.6%～42.07%之间，而采用线性土压力法计算的坑底水平位移都大于监测值，且在线性法土压力下选用工程地质规范的m值进行计算的水平位移与监测值差距最小，幅度仅有11.23%与25%。在工况五时，不同方法计算的坑底位移与监测值差距各不相同，其中，线性法土压力下选用经验公式求出的m值计算的坑底位移与监测值相差最大，前者比后者大了55.75%，而线性法土压力下选用工程地质规范的m值和朗肯土压力法选用经验公式求出的m值计算的坑底位移则相对较小，其变化幅度分别为28.7%，2.4%。

对基坑监测的最大水平位移随工况的变化(开挖0.5 m，开挖4.5 m，开挖7.9 m)进行拟合，其拟合曲线如图8所示。

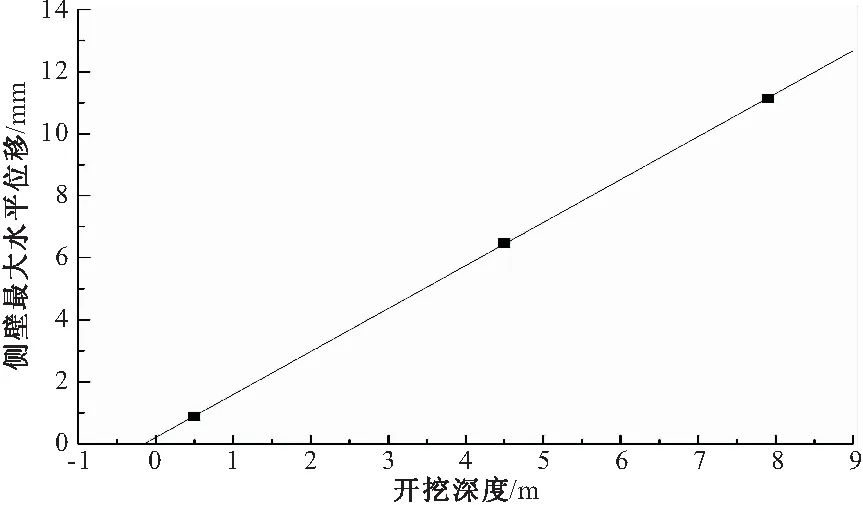
图8 最大水平位移随开挖拟合图

从拟合图中可以看出，其拟合曲线为y=1.386+0.202x，R2=0.999，可认为其拟合函数符合一次函数y=a+bx，随着开挖深度的增加，其最大水平位移也在逐渐增加。支锚工况会影响一次函数系数的取值，但是趋势不会改变，水平位移值只会略微缩小。

对比发现，除了工况一与工况二，其他工况的计算桩顶位移都远远大于监测值，特别是工况五时，即开挖7.9 m时，线性法土压力下选用经验公式求出的m值计算的桩顶位移是监测值的4倍多，远远大于实际情况。本文在计算桩顶位移时，假设桩身是刚性桩，然而桩产生的是柔性变形，因此笔者认为在计算桩顶位移时可以将由转角产生的位移乘以桩身变形系数，修正后的计算公式为，

式中：Δ0为支护结构顶部水平位移；Δ为基坑底桩水平位移；α为变形系数；h为基坑开挖深度；θ为刚性转角；δot，δoc分别为三角形土压力、矩形土压力对应的柔度系数；et,ec分别为梯形土压力中三角形部分、矩形部分土压力强度；δoi为锚杆变形系数；Ti为锚杆拉力。

修正后的计算桩顶位移(以工况5为例)如图9所示：

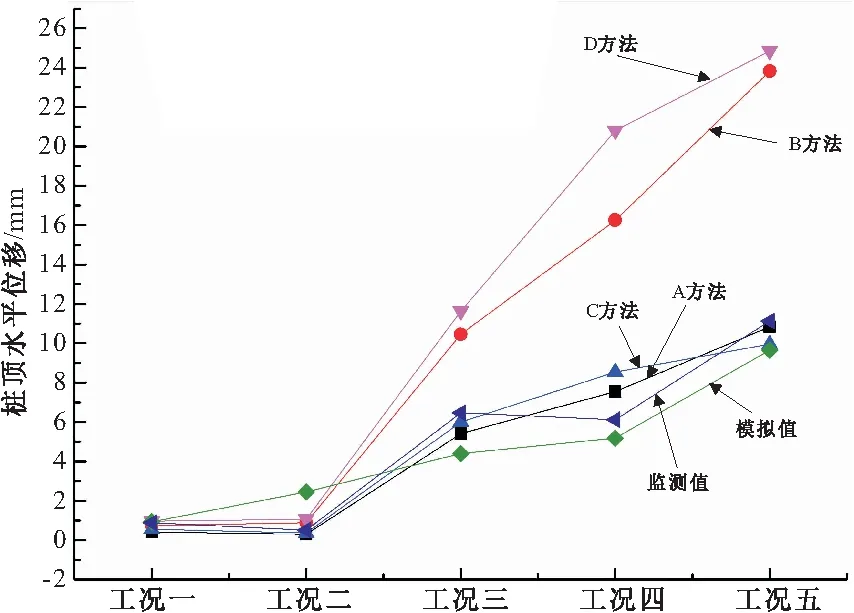
图9 修正桩顶位移与监测值、模拟值对比

从图中可以看出，采用朗肯土压力计算的桩顶位移与监测值和模拟值都比较接近，两者相差小于20%，但是除了工况四，其他工况下计算的桩顶位移都是小于监测值，其对于基坑的安全是不利的。线性法土压力计算的桩顶位移远大于监测值，且计算的桩顶位移是监测值的两倍，其计算对于基坑而言是偏于安全的。

对比监测值与模拟值，除了在支锚的工况一、工况二阶段模拟值大于监测值，其他工况下桩顶位移的模拟值皆小于监测值。发现在工况二与工况三时，两者相差较大，其值为2.2，2.5 mm。在工况一与工况四时，两者相差较小，差值为1.2，1.3 mm。这是由于实际监测点是在土方开挖后护坡形成时放置，而桩顶水平位移的模拟值是与上部土方放坡开挖同步进行的，这与加载值存在连续性也有关。