制冷离心机用高速永磁电动机转子强度设计

2019-07-02张小波贾金信

微特电机 2019年6期

张小波，贾金信，张芳

(1.空调设备及系统运行节能国家重点实验室，珠海 519070； 2.珠海格力电器股份有限公司，珠海 519070)

0 引言

高速永磁电动机由于具有功率密度高、体积小、效率高等诸多优点，成为离心压缩机用电动机的首选[1]。高速转子用钕铁硼，机械强度低，高速旋转易造成磁钢爆裂，需对磁钢进行外在特殊的保护设计[2]。当前，比较成熟的措施为非金属碳纤维护套和高强度非导磁合金护套[3]，其中碳纤维护套基本消除了护套中的涡流损耗，在降低转子损耗方面有显著优势。但是，用于制冷离心机的高速转子长期处于冷媒环境中，这些制冷剂对碳纤维护套中的固化树脂有一定的腐蚀作用，对其长期可靠性产生不利影响。因此，目前制冷离心机用高速转子多采用工艺制作简单的高强度非导磁合金护套。

采用合金保护套的转子会在护套中产生较大的涡流损耗[4-5]，同时离心机运行在高压差、高温制冷等恶劣工况时，电机发热更加严重，转子温度过高，引起转子配合过盈量减小，造成转轴强度、刚度下降，极易导致转子失效。因此，在进行高速转子强度设计时，必须考虑温度的影响。目前，相关文献仅进行了解析推导，并未考虑温度影响[6-7]，或者仅是简单的温度补偿，并未给出详细的计算方法[8]。此外，合金护套厚度也是至关重要的一个参数，护套过厚，则成本、护套上的损耗等都会增加；而护套过薄，则机械强度会下降。如何合理设计护套厚度，目前也极少有文献报道。本文对高速转子强度设计进行了详细的解析推导，并考虑温度因素，给出了有效的装配过盈量计算方法；同时从机械强度方面，给出了护套最小厚度计算方法；最后，通过有限元法和超速试验，验证了理论方法的正确性。

1 模型及计算原理

高速电机转子合金护套与磁钢的两端不封闭，沿轴向长度方向的轴向力非常小，可以视为轴向应力为零，设计时将三个方向应力状态变为两方向应力状态。基于厚壁圆筒的过盈联结计算理论，结合拉梅公式[9]，进行合金护套与磁钢的过盈设计。图1为转子拓扑结构，rm为磁钢内圆半径，rs为保护套外圆半径，rf为结合面半径。

图1 高速转子截面图

1.1 过盈应力计算

采用横向过盈联结的护套和磁钢，在结合面上产生一定的均压p，根据拉梅公式，对于仅受均匀内压p作用的护套，应力分量如下:

(1)

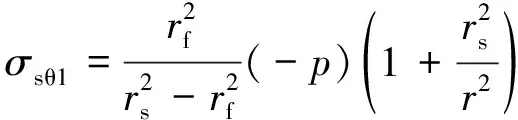
(2)

式中：σsr1,σsθ1分别为护套静态应力的径向和切向分量。

对于仅受均匀外压p作用的转子磁钢，应力分量如下:

(3)

(4)

式中：σmr1，σmθ1分别为磁钢静态应力的径向和切向分量。

1.2 考虑旋转离心力及温度因素的过盈量计算

考虑高速离心力的作用，护套和磁钢都会发生位移，配合面的过盈量也会随着旋转发生变化。考虑旋转效应，由拉梅公式和空心轴的本构方程，动态时护套的应力分量和位移分量:

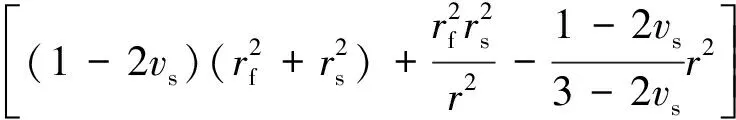
(7)

式中：σsr2，σsθ2分别为护套动态应力的径向和切向分量；μsr2为护套的动态径向位移；vs为护套的泊松比；ρs为护套的密度。

同理，动态时磁钢的应力分量和位移分量:

式中：σmr2，σmθ2分别为磁钢动态应力的径向和切向分量；ρm为磁钢密度；vm为磁钢的泊松比；ω为机械角速度；Em为磁钢的弹性模量。

考虑旋转效应，护套与磁钢之间过盈减少量可通过式(7)和式(10)计算：

Δδ=μsr2|r=rf-μmr2|r=rf

(11)

假设护套与磁钢接触面的装配过盈量为δ，可得永磁体与护套间动态过盈量：

δd=δ-Δδ

(12)

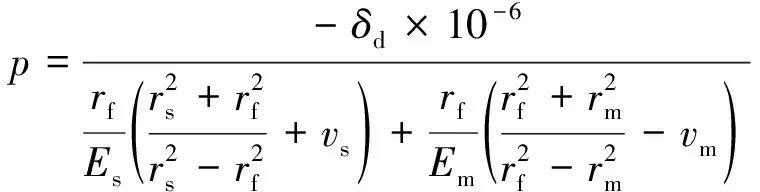
(13)

式中：Es为护套的弹性模量。

综合考虑过盈配合静压力作用和旋转效应，转子动态运行时，护套和永磁体的应力计算需将两者叠加，则内表面受均匀内压p的护套、磁钢的应力分量及护套的米塞斯等效应力：

σsr=σsr1+σsr2

(14)

σsθ=σsθ1+σsθ2

(15)

σmr=σmr1+σmr2

(16)

σmθ=σmθ1+σmθ2

(17)

(18)

对于采用合金类塑性材料的护套，第四强度理论(米塞斯理论)比第三强度理论更符合试验结果。护套的最大等效应力σsvon-Mises需满足以下条件：

σsvon-Mises≤[σs]

(19)

磁钢为脆性材料，应力评判采用第一强度理论(最大拉应力理论)较为适合。因此，磁钢的最大拉应力应满足以下条件：

σmθ≤[σm]

(20)

高速转子装配过盈设计时，必须考虑温度的影响，在常温设计过盈量的基础上增加额外的温度导致的过盈减小量。考虑温度因素的过盈减小修正量：

δt=(αs-αm)(Tω-T0)rf

(21)

式中：αs，αm分别为护套和磁钢的线膨胀系数；Tω为转子工作温度；T0为常温。

2 过盈量及应力解析法计算

2.1 装配过盈量计算

电机额定转速ne=40 000 r/min，按1.2ne设计，即48 000 r/min。护套和磁钢的安全系数取1.5，即护套和磁钢的许用应力[σs]，[σm]分别为800 MPa和53.3 MPa。rs，rf，rm分为35 mm，32 mm和20 mm。Tω和T0分别为100 ℃和20 ℃，磁钢及护套物性如表1所示。

表1 磁钢与护套物性

转子过盈量计算流程如图2所示。输入转子尺寸及材料属性，可得Δδ=0.018 1 mm，并计算出温度因素导致的过盈量减小量δt=0.02 mm，给定初始装配过盈量δ，迭代直至满足判定条件。如表2所示，第n次迭代，δ取0.082 7 mm时，磁钢最大拉应力接近其许用应力，护套最大等效应力688 MPa,小于其许用应力；第n+1次迭代，δ取0.102 7 mm时，磁钢应力下降至24 MPa,小于其许用应力，护套最大等效应力792 MPa,接近其许用应力。则考虑温度影响，最终装配过盈量δf=0.122 7 mm。

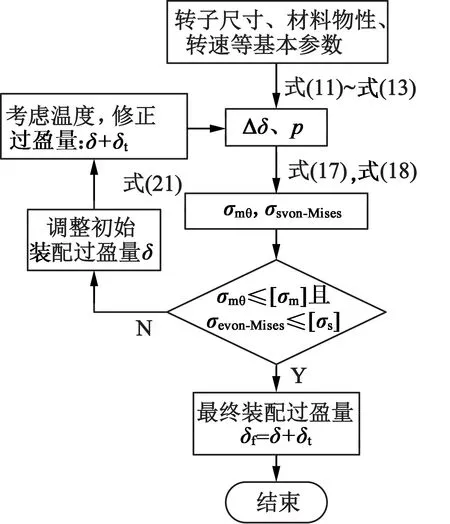
图2 转子过盈量计算流程图

δ/mmδd/mmp/MPaσmθ/MPaσsvon-Mises/MPan0.082 70.084 6-37.553688n+10.102 70.105-46.424792

2.2 解析法应力计算

考虑加工精度，实际装配过盈量δf取0.123 mm。采用解析法计算磁钢内和护套的应力分布，如表3、表4所示。其中，负号表示压应力，正号表示拉应力。在此过盈量下，护套48 000 r/min运行时，磁钢外表面压应力46.5 MPa，磁钢最大拉应力23.5 MPa，小于其许用应力；护套最大等效应力793.6 MPa，小于其许用应力。

表3 解析法计算磁钢应力

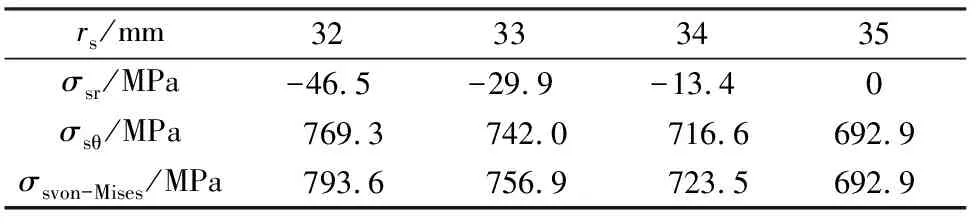
表4 解析法计算的护套应力

3 有限元仿真验证及对比分析

3.1 转子护套及磁钢应力有限元验证

建立三维有限元全模型，详细研究了护套及磁钢在轴向对称中心和端部边缘处沿径向的应力分布，应力取点如图3所示。

图3 转子模型截面图

在过盈量为0.123 mm，转速48 000 r/min条件下，采用有限元法和解析法计算的护套和磁钢的应力范围详见表5。由表5可知，无论是磁钢还是护套，各种应力采用解析法和采用有限元法计算的结果具有较高的吻合性，最大偏差仅为1.89%。

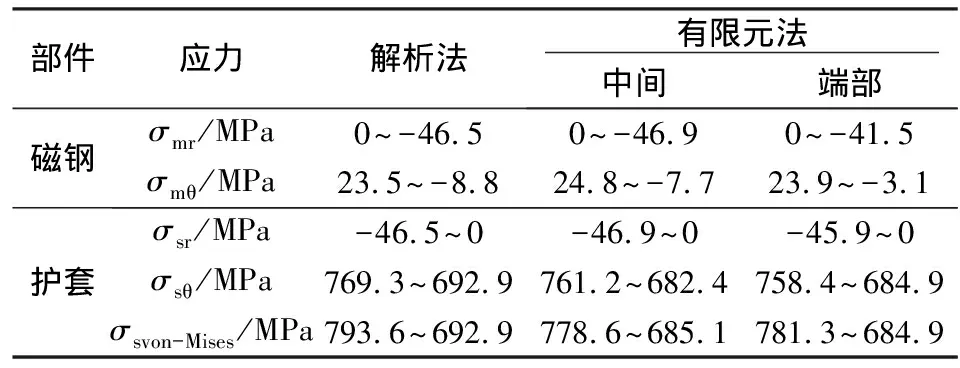
表5 解析法与有限元法计算的应力范围

如图4所示，磁钢径向应力随磁钢半径的增加而增加，径向一直处于受压状态；而切向应力随半径的增加逐渐减小至0，再逐渐由0变为-8.8 MPa，即

图4 磁钢应力对比图

由拉应力变为压应力状态。在不同半径处，采用解析法和有限元法计算的磁钢的径向和切向应力均有较高的一致性，且沿磁钢中间处采用有限元法获得的径向和切向应力均与解析法获得的应力更为接近，而在端面处采用有限元法计算偏差会大一些，特别是在靠近结合面处，偏差约1.15%。

如图5所示，护套径向应力随护套半径的增加而减小，径向一直处于受压状态；而切向应力随半径的增加也逐渐减小，并一直处于拉应力状态；等效应力同样随半径的增加也逐渐减小。在不同半径处，采用解析法和有限元法计算的护套的径向、切向和等效应力均有较高的一致性，且沿护套中间处采用有限元法获得的径向和切向应力与解析法获得的应力更为接近，而在沿护套端面处采用有限元法获得的等效应力与解析法获得的应力更为接近，在中间处反而偏差会大一些，偏差约1.89%。如图6所示，分别显示了转子护套、磁钢的径向、切向和等效应力分布，每张图的应力极值分别为整个磁钢或护套区域的最大值和最小值。

图5 护套应力对比图

(a) 磁钢径向应力σmr

(b) 磁钢切向应力σmθ

(d) 护套切向应力σsθ

(e) 磁钢等效应力σme

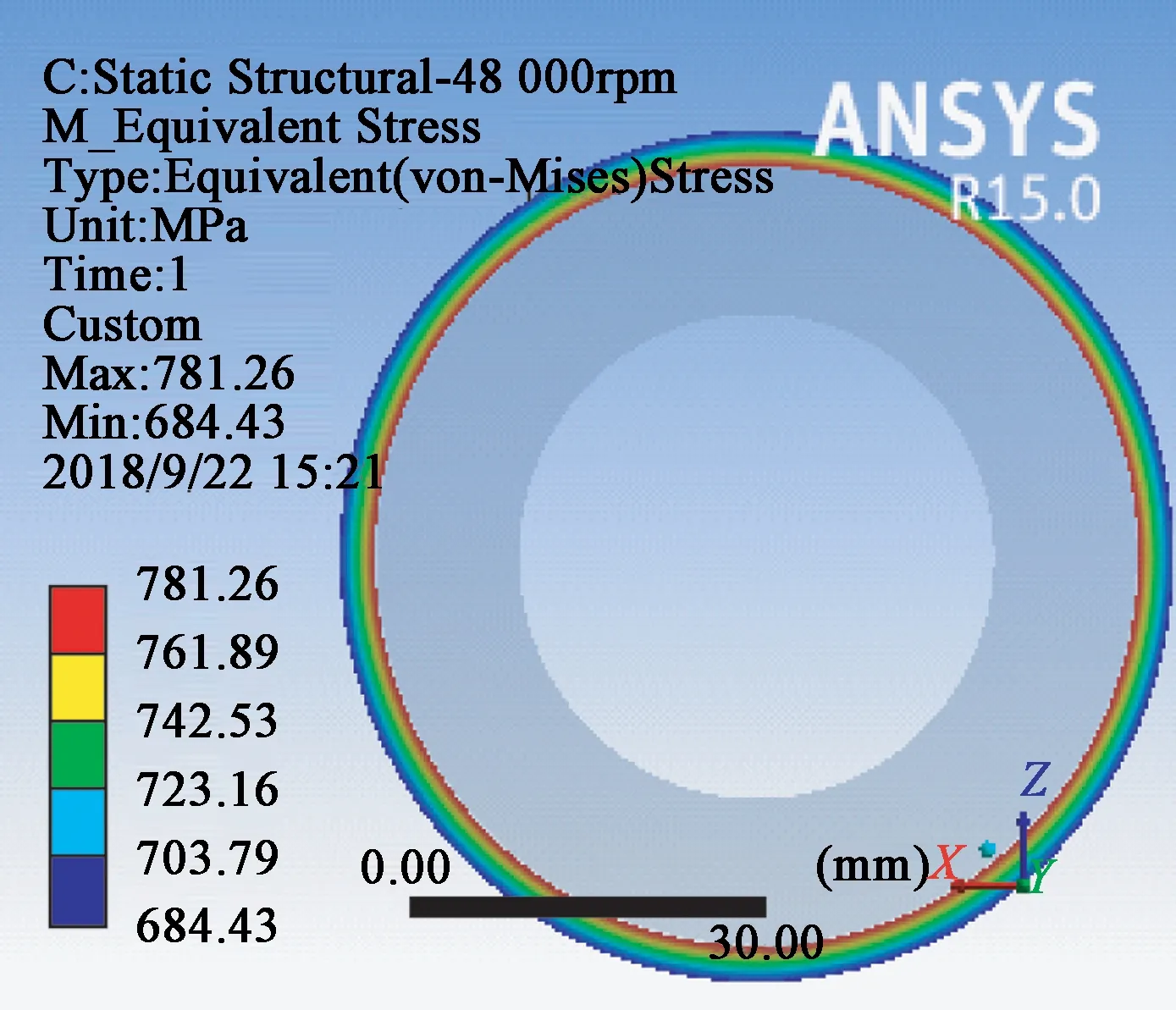
(f) 护套等效应力σse

3.2 护套厚度设计

采用解析法计算了不同护套厚度下磁钢外表面径向应力和内表面的最大切向应力及护套的最大等效应力。由图7可知，护套的最大等效应力和磁钢的内表面切向拉应力均随着护套厚度的增加逐渐减小；同时，磁钢表面的压应力逐渐增加。可见，增加护套厚度可显著提高转子各部件的可靠性。护套厚度必须使得磁钢和护套的应力均在其安全界限内，通过图7可以确定护套的最小厚度为2.75mm，因此本设计选取护套厚度3mm是合理的。