一种考虑节点功率的电网连锁跳闸评估方法
2019-07-01EyhabAlaini
EyhabAlaini
(福建工程学院 信息科学与工程学院,福建 福州 350118)
电网连锁故障是引起大停电事故的主要原因,近些年来这一问题受到了很多研究者的关注。他们从连锁故障的发生机理,连锁故障的模拟,连锁故障的风险分析,电网结构对连锁故障的传播作用等方面对连锁故障进行了研究[1-3],取得了很多有益的研究成果,对进一步研究电网连锁故障提供了帮助。
电网连锁故障最常见的形式是连锁跳闸,其具体的表现方式为:当电网中的一条支路因初始故障停运后,其他的某些支路因为潮流重新分配而进入后备保护的动作区内而被切除。这一现象在电网连锁故障的早期阶段尤其如此。最近20 a来,从世界范围来看,几乎每隔一段时间就有一次大停电事故发生。这些停电事故一般具有连锁故障的特征,而且在连锁故障的早期阶段,也都表现为连锁跳闸。
尽管,随着现代计算机、通信以及控制技术的发展,电力系统的自动化水平有了很大的提升,但是连锁跳闸以及连锁故障仍有发生,说明人们对连锁跳闸及连锁故障的重视不够或认识上存在不足。
电网的连锁跳闸,一般和线路的后备保护的动作密切相关[4]。而且,在初始故障线路停运后,电网是否因潮流的重新分布而发生连锁跳闸,和初始故障前的电网运行状态有很大关系。本文综合考虑了常见的电流型及距离型后备保护的动作行为,并依据该动作行为分析了电网连锁跳闸与电网节点注入功率之间的关系,然后提出了一种基于模式识别技术的连锁跳闸评估方法。该方法以电网的节点注入功率为特征输入量,以是否发生连锁跳闸为输出量,在利用样本数据形成分类器后,对于任意的运行状态,可根据输入的节点注入功率向量来评估在该运行状态下电网是否会因某初始故障而发生连锁跳闸。最后,采用IEEE39系统进行运算演示,在该算例中,本文提出的基于模式识别技术的连锁跳闸评估方法,其评估正确率很高,说明该方法是有效的。
1 考虑后备保护时的电网连锁跳闸行为分析
由于电网的连锁跳闸一般是在初始故障后由潮流的重新分布引起的,这个过程较慢,所以发生连锁跳闸的线路一般都是由继电保护中的后备保护切除的[4]。在高压输电网中,线路一般都配置三段式距离保护,其中距离Ⅲ段保护主要用作延时动作切除故障,在初始故障后的电网潮流转移过程中,距离Ⅲ段是可能动作的保护之一。除了距离保护以外,有的电网还配置过负荷保护,过负荷保护可能发出告警信息,也可能延时动作跳闸,如果采用延时跳闸的方式,则在初始故障后的电网潮流转移过程中,这类后备保护也可能动作。
无论是过负荷保护还是距离Ⅲ段保护,都可以根据其动作方程采用统一的表达形式来衡量相应的支路是否发生连锁跳闸。设某电网中发生初始故障的支路为支路Lij(介于节点i与节点j之间的支路,文中其他支路的表示方法与此相同),则当电网的潮流重新分配后,电网剩余系统中任一支路Lst的情况可结合后备保护的动作方程来考虑。设潮流重新分布后支路Lst的电压、电流的参考方向如图1所示。

图1 支路Lst的电压和电流Fig.1 Voltage and current of Branch Lst
对于Lst的s侧的后备保护而言,其是否会发生连锁跳闸可采用式(1)来进行衡量[5]。
ωs·dist=|ωs·lim|-|ωs|
(1)
式中,ωs·lim是支路Lst的s侧的后备保护的动作方程中由保护的定值构成的参量,ωs是支路Lst的s侧后备保护的动作方程中由保护的定值和测量值构成的参量,ωs·dist是衡量ωs·lim和ωs之间电气距离的参量。当ωs·dist≤0时,支路Lst的s侧后备保护将会跳闸,而当ωs·dist>0时,支路Lst的s侧后备保护将不会跳闸。
式(1)给出的判断方程是以支路Lst的s侧保护给出的,对于支路Lst的t侧保护来说,其判断的形式与式(1)一致,只是相应的下标字母由s变为t,如ωs改为ωt,则相应的判断式变为式(2)。
ωt·dist=|ωt·lim|-|ωt|
(2)
对于ωs·lim和ωs的具体形式,当后备保护为过负荷保护时,则ωs·lim可取为支路Lst的s侧的过负荷保护的电流定值Is·set,而ωs可取为流过支路Lst的电流Ist;相应地,对于Lst的t侧的后备保护而言,ωt·lim可取为支路Lst的t侧的过负荷保护的电流定值It·set,而ωt可取为电流Its。
对于后备保护为距离Ⅲ段保护的情况,若后备保护为偏移圆特性的距离保护,则对于支路Lst的s侧保护来说可参照文献[6],参量ωs·lim的具体形式可取为:
ωs·lim=(Zs·set1-Zs·set2)/2
(3)
式中,Zs·set1和Zs·set2为支路Lst的s侧距离Ⅲ段保护的定值。而此时,ωs的具体形式可分别取为:
ωs=Zs·m-(Zs·set1+Zs·set2)/2
(4)
式中,Zs·m为支路Lst的s侧距离Ⅲ段保护的阻抗测量量,结合图1,该量可由式(5)给出。
(5)
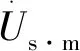
对于支路Lst的t侧距离Ⅲ段保护可类似地按式(3)-(5)对应处理。
若保护为具有方向的圆特性的距离保护,则参量ωs·lim的具体形式可取为[5-6]:
ωs·lim=Zs·set/2
(6)
式中,Zs·set为支路Lst的s侧距离Ⅲ段的定值。而此种情况下,Zs可取为[5-6]:
ωs=Zs·m-Zs·set/2
(7)
式中,Zs·m的含义和获取与式(4)、(5)中的一致。
同样地,对于支路Lst的t侧距离Ⅲ段保护可类似地按式(6)、(7)对应处理。
若保护为具有全阻抗特性圆方向特性的距离保护,则参量ωs·lim的具体形式可取为[5-6]:
ωs·lim=Zs·set
(8)
而此时,ωs为:
ωs=Zs·m
(9)
同样,对于支路Lst的t侧距离Ⅲ段保护可类似地按式(8)、(9)对应处理。
除此以外,若支路Lst的距离Ⅲ段后备保护采用的是其他形式的动作特性,则可以按照上述方法给出ωs和ωs·lim的值。
2 连锁跳闸的主要决定因素分析
从前面的分析可见,在初始故障支路停运后,电网任一支路Lst是否发生连锁跳闸主要由式(1)中的ωs·dist决定。在支路Lst的保护定值已经确定的情况下,决定ωs·dist的主要因素是ωs,而ωs则决定于支路Lst的后备保护的测量电流,或由测量电压和测量电流共同决定。由继电保护的知识可知,支路Lst的后备保护的测量电流和测量电压则主要决定于潮流重新分布后节点s和节点t的电压以及流过支路Lst的电流,在支路Lst的参数固定的情况下,流过支路Lst的电流主要决定于节点s和节点t的电压。综合上述分析可见,电网任一支路Lst是否发生连锁跳闸主要决定于潮流重新分布后节点s和节点t的电压。
进一步地,由电力系统潮流计算的知识可知,当支路Lij发生初始故障停运后,电网的方程为:
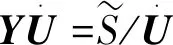
(10)

综合以上分析,在初始故障支路停运后,电网任一支路Lst是否发生连锁跳闸主要决定于支路Lij停运前电网的节点注入功率。也就是说,在电网的结构、元件参数以及保护的定值固定的情况下,对于支路Lij发生初始故障而言,决定任一支路Lst是否发生连锁跳闸的主要因素是电网的节点注入功率。
3 电网连锁跳闸评估的思路和算法
前面的分析给出了两点启示,一是电网的节点注入功率与发生连锁跳闸之间具有较为严密的映射关系,二是对于不同的节点注入功率状态,若要验算该状态下电网对于某初始故障是否会发生连锁跳闸,常规的做法是通过潮流计算进行验算,计算工作量较大。考虑到这两点,若利用模式识别技术将连锁跳闸与节点注入功率之间的关系重构出来,形成分类器,然后对于任一节点注入功率状态,只要将该状态对应的节点注入功率输入到分类器中即可判别电网是否发生连锁跳闸,这将使得判别方法变得较为简单、便捷。下面给出采用模式识别技术进行连锁跳闸评估的基本思路。
3.1 评估的输入变量和输出变量
根据前面的分析,节点注入功率对连锁跳闸结果的决定作用,在采用模式识别技术进行评估时,可将节点注入功率作为输入量,将是否发生连锁跳闸的结果作为输出量。
对于输入量,用S来表示,并设电网有n个节点,其表示形式可写成向量的形式:
P=[P1,Q1,…,Pj,Qj,…,Pn,Qn]T
(11)
式中,向量P的元素Pj,Qj分别表示任一节点j注入的有功功率和无功功率,可见P共有2n维。
对于输出量,用y来表示。因为要判别电网是否发生连锁跳闸,涉及到剩余系统的所有支路,为了便于量化分析,这里将式(1)扩充为式(12)。
D=min(ωst.dist)
(12)
显然,由式(1)及式(12)可知,在初始故障支路Lij停运后,如果满足D>0,则电网不会没有连锁跳闸,此时可取y=0;如果满足D≤0,则电网中至少有一条支路发生连锁跳闸或处于连锁跳闸的边界, 此时可取y=1。
3.2 评估的思路
给定了输入、输出数据的规范表达形式后,将输入量P与输出量y综合起来,即可形成式(13)所示的样本数据。
Si=[P1,Q1,…,Pj,Qj,…,Pn,Qn,y]T
(13)
式中,Si表示样本i,显然,Si是一个2n+1维的列向量,若有N个样本,则i=1,2,…,N。
有了样本数据之后,即可按照模式识别的一般思路给出连锁跳闸评估的思路,这个思路是:先利用一部分样本数据通过训练形成分类器,然后再利用一部分样本数据对训练好的分类器进行测试,通过测试正确率符合要求,则以后就采用该分类器进行连锁跳闸的评估,即针对每一个节点注入功率状态,将表征该节点注入功率状态的P输入到分类器中,然后根据输出的结果来评估电网是否发生连锁跳闸。如果分类器经测试不符合要求,则重新训练,直到其符合要求为止。
其中,在形成样本数据时,需要注意的是要考虑电网中实际的后备保护的配置。无论是电网配置了电流型后备保护,还是距离型后备保护,或者是这二者都有,在按式(12)形成y值时,都应严格与电网的实际配置相对应。
以上给出的是一个基于模式识别技术进行连锁跳闸评估的基本思路,至于在实际当中采用何种具体的模式识别技术,这可以根据实际的需要和具体情况加以选择,文中不做详细讨论。为了演示算例,本文将在算例部分给出一种基于BP神经网络的评估方法。
4 算例
本文以IEEE 39节点系统进行算例分析,其系统接线图如图2所示。
在算例中,本文在MATLAB环境下编制了分析程序。程序主要包括样本数据形成和分类器训练及测试几个部分。在算例中主要针对电网配置电流型后备保护、距离保护以及既配置电流保护和距离保护的3种情况给出了算例,其中第3种情况本文称之为混合型。
在形成样本数据时,本文的主要操作步骤如下:
(1)设定初始故障。
(2)获取节点注入功率状态。
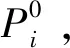
ΔP=ΔQ=50×rand(1,1)
(14)
式中的rand为MATLAB在(0,1)区间获取一个随机数的函数。
然后对于任一的PV节点,按式(15)进行操作。
(15)
对任一PQ节点,按式(16)进行操作。
(16)

图2 算例系统接线图Fig.2 Wiring diagram of the example system
这里,对于那些原典型数据中为P=Q=0的节点,本文不再按式(16)进行操作,仍然将其保持为P=Q=0。
这样操作之后,就可以获得一个新的节点注入功率状态及其对应的节点注入功率向量P。
(3)获取y值及形成样本。
获取y值时,本文根据设定的初始故障,对其开断后的电网潮流进行计算,然后根据式(12)判断电网是否发生连锁跳闸,对于发生连锁跳闸的情况,将y取为1,否则,取y为0。然后再根据式(13)将P和y组合起来,形成一个样本。
然后重复上述操作,直到得到足够数量的样本。
接下来,对得到的样本进行训练和测试。这里本文采用MATLAB工具箱中的函数。其中初始化函数为newff,其调用形式为:
net=newff(input,output,8)
(17)
式(16)input和output分别为输入量和输出量,在这里分别为P和y。
训练函数选MATLAB工具箱中的train,其调用形式为:
net=train(net,input,output)
(18)
相应地,对于train中的一些参数,在本算例中trainParas.epochs取为500,trainParas.lr取为0.1,trainParas.goal取为0.002。其他的参数采用其缺省值。
测试函数选MATLAB工具箱中的train,其调用形式为:
PreOutput=sim(net,input_test)
(19)
式中input_test为用于测试的输入数据,PreOutput为预测输出量。
对于输入量P的归一化处理,本算例选mapsinsax进行。
图3给出了电网配置电流型保护时的一个例子,初始故障支路为支路L4-5,其样本数据总数为200,其中120个样本用于训练,80个样本用于测试,计算的结果,测试正确率为98.45%,如果以90%的正确作为标准来衡量的,这个测试结果是满足要求的。
图4给出了电网配置距离型保护时的一个例子,初始故障支路为支路L21-22,其样本数据总数也为200,其中80个样本用于训练,120个样本用于测试,计算的结果,测试正确率为99.13%,显然,这个训练结果也是令人满意的。
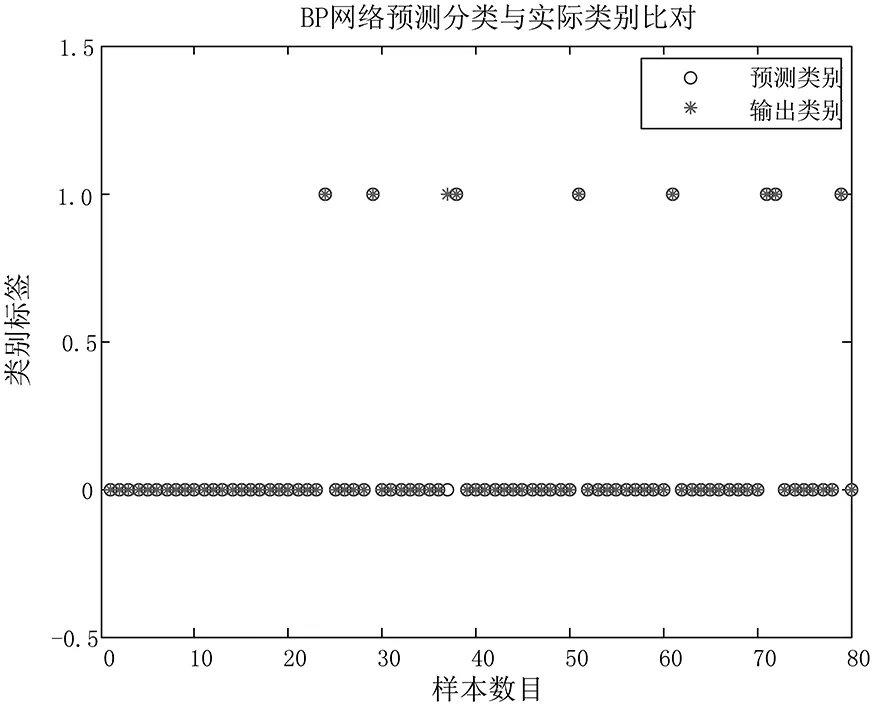
图3 电网配置电流型保护时分类器测试情况Fig.3 Testing of classifiers in power network configuration of current-mode protection

图4 电网配置距离型保护时分类器测试情况Fig.4 Testing of classifiers in power network configuration of distance-mode protection
图4的例子中,距离保护Ⅲ段采用全阻抗圆特性的保护,在利用式(12)判断支路连锁跳闸时以按支路扫描的方式进行,这样做实际上已经考虑了距离保护的方向性。
图5给出了电网配置混合型保护时的一个例子,初始故障支路为L21-22,其样本数据总数为300,其中210个样本用于训练,90个样本用于测试,测试正确率为97.75%,这个测试结果也是令人满意的。
与图5对应的例子中,在形成样本数据时,距离型保护和电流型保护的动作都要考虑,对于这两类保护,其中任何一类动作都看作有连锁跳闸发生。对于距离型保护,这里仍按全阻抗圆特性来考虑。

图5 电网配置混合型保护时分类器测试情况Fig.5 Testing of classifiers in power network configuration of mixed protection
通过图3、4、5给出的分类器测试结果是比较令人满意的。当然,分类器还可以进一步改进,比如调整分类器的训练参数,利用其它的模式识别技术等等,限于篇幅,本文不再对此深入讨论。
从上面给出的例子还可以看出,一旦得到满意的分类器时,对任一节点注入功率状态,只需输入表征该节点注入功率状态的节点功率向量即可评估是否会被给定的初始故障引起连锁跳闸,而不必每次都对初始故障切除后的潮流进行计算,这是采用模式识别技术的优势所在。
5 结论
电网的连锁跳闸现象与线路的后备保护动作、电网的结构、电网的运行状态等众多因素有关,本文的研究主要有以下结论:
1)当电网的结构和元件参数固定,且当线路后备保护的定值固定时,不论后备保护是电流型的还是距离型的,或者是既有电流型也有距离型后备保护,对于给定的初始故障,电网是否因该初始故障而发生连锁跳闸,其主要的决定因素在于电网的节点注入功率。
2)无论电网的线路采用的是电流型还是距离型保护,或既有电流型也有距离型后备保护,都可以采用模式识别技术进行电网连锁跳闸的评估。
3)利用模式识别方法进行电网的连锁跳闸评估,一旦得到满意的分类器时,对任一节点注入功率状态,只需输入相应的节点功率向量即可进行评估,而不必对初始故障切除后的潮流进行计算,这使得连锁跳闸的评估变得简洁。
本文研究所得的结论,以及提出的基于模式识别技术的连锁跳闸评估方法对于进一步的研究及实际的电网运行有一定的借鉴。
