铝合金框架结构二阶效应的有限元分析
2019-07-01张铮黄娟娟谈夏维廖仁生
张铮,黄娟娟,谈夏维,廖仁生
(1.闽台合作土木工程技术福建省高校工程研究中心,福建 福州 350118;2.福建工程学院 土木工程学院,福建 福州 350118)
铝合金材料因为密度小、质量轻、防腐蚀性能好、低温韧性好、可循环利用等优点而得到广泛应用。通常把与0.2%残余应变相对应的应力定为铝合金材料的名义屈服强度。与低碳钢相比,铝合金材料的弹性模量只有钢材的三分之一左右,而且铝合金材料的应力应变曲线没有与屈服阶段对应的屈服平台,在其材料承载能力达到名义屈服强度之前就已有相当明显的塑性变形,而钢材在达到屈服强度之前仍处于弹性变形。相对于钢框架结构,铝合金框架结构因材料非线性产生的影响更为突出[1]。
国内对铝合金框架非线性分析的现有研究[2]仅考虑了框架的几何非线性,对于材料的非线性没有考虑。《铝合金结构设计规范》(GB 50429-2007)[3]提出的近似二阶弹性分析的计算方法,是在弹性范围内考虑二阶效应,未考虑材料非线性的影响。能否对铝合金框架结构进行准确的受力分析并进行合理的设计,将影响整体结构的适用性和安全性。因此,铝合金框架结构设计是否考虑材料非线性的影响有待于进一步研究。
为了考察铝合金框架结构同时考虑几何非线性和材料非线性的实际受力情况,分别对弱硬化合金6061-T6和强硬化合金6061-T4两种工程中常用典型合金类型的铝合金框架结构进行了一阶弹性分析、二阶弹性分析和二阶弹塑性分析,并与现行规范规定的近似计算方法的计算结果进行比较,分析规范近似计算方法对铝合金框架设计的适用性,以获得可供工程实践参考的结果。
1 铝合金框架结构设计方法
国内对铝合金结构的研究始于20世纪80年代,20世纪90年代后我国建成了多座大跨度铝合金结构,理论研究内容也日趋广泛,并于2008年颁布《铝合金结构设计规范》(GB 50429-2007)[3]。规范在编写过程中主要参考了国外的研究成果和欧洲规范,规范编写组力求将铝合金构件、连接、板件等计算公式与《钢结构设计规范》(GB 50017-2017)[4]以及《冷弯薄壁型钢结构技术规范》(GB 50018-2002)[5]中的相关公式在形式上统一起来,以便应用[6]。
《铝合金结构设计规范》(GB 50429-2007)[3]中框架结构设计使用的近似计算方法是在结构各层柱顶施加与楼层总竖向荷载或构件轴力成正比的假想水平力,从而间接考虑残余应力、初始几何缺陷等非线性因素影响。假想水平力的计算公式为
(1)

《铝合金结构设计规范》(GB 50429-2007)[3]规定:对所有框架(有无支撑结构)均可采用一阶弹性分析方法计算框架杆件的内力,但对于满足(2)式的框架结构则推荐采用二阶弹性分析确定。
(2)
对无支撑的框架结构,当采用二阶弹性分析时,各杆件杆端的弯矩MII可用式(3)、(4)近似计算
MII=MIb+α2iMIs
(3)
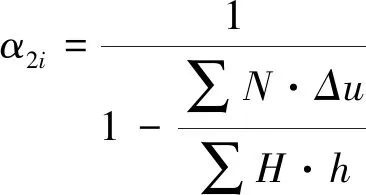
(4)
式中,∑N为所计算楼层的各柱轴心压力设计值之和;Δu为按一阶弹性分析求得的所计算楼层的层间侧移;∑H为产生层间侧移Δu的所计算楼层及以上各层的水平力之和;h为所计算楼层的高度;MIb为假定框架无侧移时按一阶弹性分析求得的各杆杆端弯矩;MIs为框架各节点侧移时按一阶弹性分析求得的各杆杆端弯矩;α2i为考虑二阶效应第i层杆件的侧移弯矩增大系数。
当∑N·Δu/(∑H·h) ≤ 0.1时,说明框架结构的抗侧移刚度较大,可忽略侧移对内力分析的影响,故可采用一阶分析法来计算框架内力,也不必考虑假象水平力Hni;当∑N·Δu/(∑H·h) > 0.25时,式(3)误差较大,应适当增加框架结构的侧移刚度或采用精确二阶弹性分析,使α2i≤1.33。
可见,我国铝合金结构设计规范中对二阶效应的规定与钢结构规范中的基本相同,这是因为处于弹性阶段的金属框架结构其二阶效应的理论相同[7]。在钢框架结构中,一般先忽略材料屈服,而把注意力集中在结构的弹性特征上。而在铝合金框架结构中,由于铝合金材料非线性明显,利用材料弹性区域进行设计,只考虑结构的弹性特征是否能满足设计要求,需要进一步探索。
2 数值分析
铝合金的种类、牌号很多,为了能更好地反映不同合金类型的铝合金框架结构的受力性能,选用工程中常用的弱硬化合金6061-T6和强硬化合金6061-T4两种典型合金类型的铝合金框架结构进行有限元分析,选取的算例包括单层单跨、两层单跨和两层两跨3种。
构件在进行有限元建模时采用梁单元B21,铝合金的材料性能按照《铝合金结构设计规范》(GB 50429-2007)[3]规定取值。铝材弹性模量E取70 000 MPa,泊松比υ为0.3。其中,6061-T6合金的名义屈服强度f0.2取245 MPa,6061-T4合金的名义屈服强度f0.2取110 MPa。
一阶弹性分析和二阶弹性分析只考虑几何非线性,没有考虑材料非线性,因此分析时采用铝合金理想弹性本构关系模型;二阶弹塑性分析既考虑几何非线性也考虑材料非线性,材料本构关系采用Ramberg-Osgood模型[8],如式(5)所示:
(5)

算例中底部框架柱柱脚与基础、框架柱和横梁均假设为刚性连接,作用荷载为每层柱顶水平集中力和横梁上均布重力荷载,框架计算简图见图2,每个算例加载的荷载见表1,单元截面特性见表2。

图1 铝合金和钢材的应力-应变关系的比较Fig.1 Comparison of stress-strain relationship between aluminum alloy and steel
表1 各个算例荷载布置表

Tab.1 Load arrangement of each calculation example
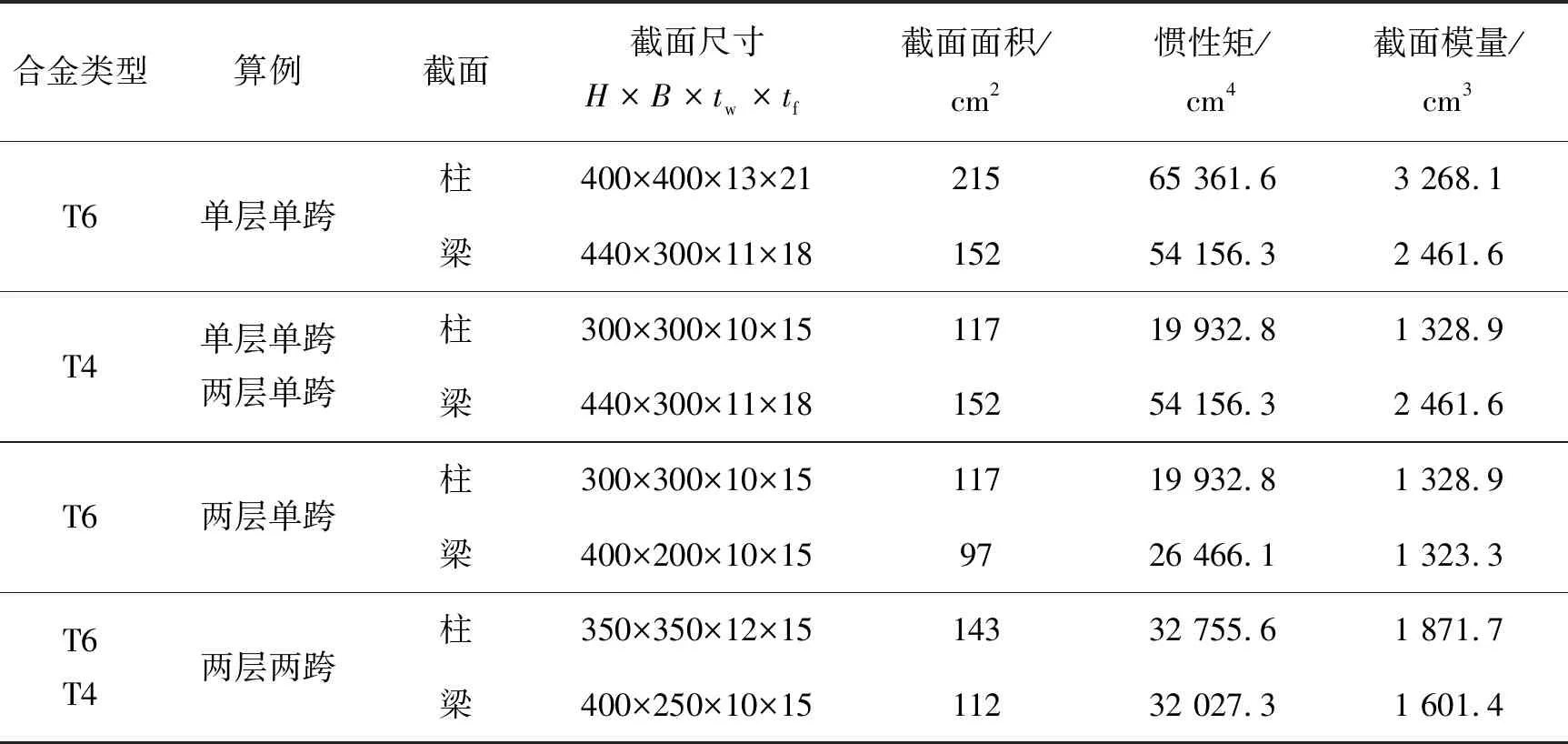
表2 截面特性表
注:截面尺寸中,H为截面高度(mm);B为截面宽度(mm);tw为腹板厚度(mm);tf为翼缘厚度(mm)。

图2 铝合金框架计算简图(单位:mm)Fig.2 Calculation diagram of aluminum alloy frame(unit: mm)
3 计算结果及分析
利用有限元软件ABAQUS计算了文献[9]的框架,验证有限元方法的正确性,再对本文6个算例进行相应的数值模拟。
各算例相关参数的计算结果见表3,表中α2i和Hni分别由式(4)和式(2)计算得出;各算例的杆端弯矩计算结果见表4和表5,表中的近似二阶弹性分析弯矩由式(3)算得。

表3 相关参数
从表3可以发现,当水平集中力不大时,各层柱顶附加的假象水平力Hni对框架侧移的影响会加大,随着框架层数越多影响会减小;但跨数增多(即各层重力荷载增加)又会加大Hni的影响,说明重力荷载增大将加大二阶效应,反之,二阶效应越不明显,与钢框架结构情况基本相同[7]。
表4和表5显示, 6061-T6合金和6061-T4合金框架二阶效应表现出相同的变化趋势,但塑性效应对6061-T4合金框架的影响更为显著,这主要是因为6061-T4合金材料塑性发展比6061-T6合金更快,从而导致两者偏差较大。
同时可以看出,单层单跨框架的二阶效应影响非常小,需要层高很大时才能满足式(1)的要求,但其材料非线性引起的塑性效应最明显,柱端内力偏差基本大于10%,其中6061-T6合金框架最高达12.2%,6061-T4合金框架最高达27.8%。
对于两层单跨的铝合金框架,随着层数增多,框架的层间侧移增量也变大,二阶效应更为突出;同时考虑几何非线性和材料非线性的二阶弹塑性分析的层间侧移增量的偏差远大于只考虑几何非线性的二阶弹性分析,其中,6061-T6合金框架最高达20.7%,6061-T4合金框架最高达到151.7%,说明层数增多会加剧侧移的增加。
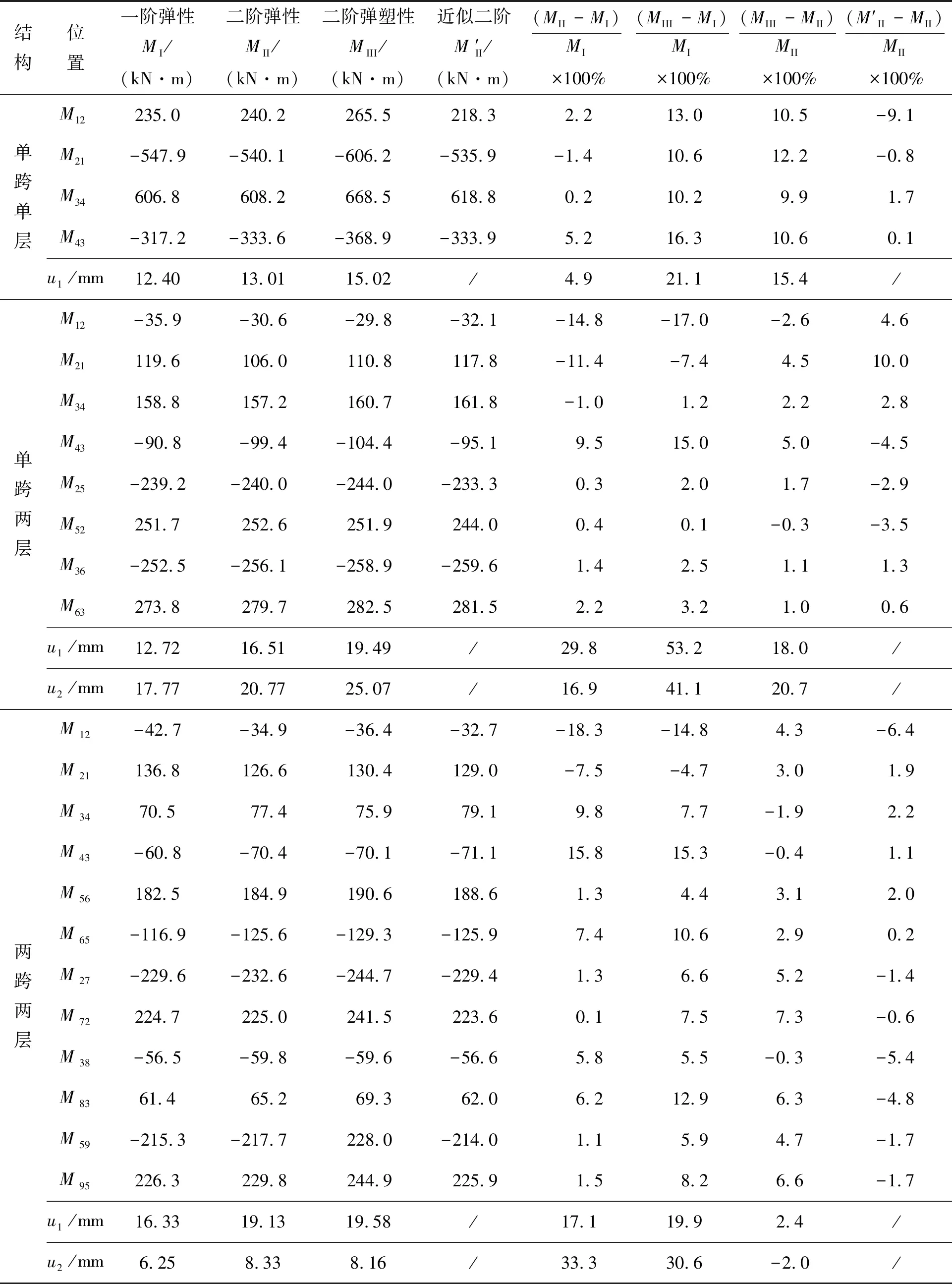
表4 6061-T6铝合金框架典型算例
注:u1为一层层间侧移;u2为二层层间侧移。

表5 6061-T4铝合金框架典型算例
注:u1为一层层间侧移;u2为二层层间侧移。
相对于两层两跨的铝合金框架,材料非线性引起的层间侧移增量小于两层单跨的框架,但是加剧了二阶效应对框架内力的影响,其中,6061-T6合金框架的内力偏差最高达7.3%,6061-T4合金框架最高达23.1%,且偏于不安全。可见,在铝合金框架设计中,框架总层数和总跨数的影响不容忽略。
而且,无论是只考虑几何非线性的二阶弹性分析,还是同时考虑几何非线性和材料非线性的二阶弹塑性分析的铝合金框架,在水平集中力作用处的底层框架柱处都有着最大的偏差,此处二阶效应也最为显著。
4 结论
1)6061-T6合金和6061-T4合金框架二阶效应和材料非线性表现出相同的变化趋势,但材料非线性引起的塑性效应对6061-T4合金框架的影响更为显著。
2)相对于二阶弹性分析与一阶弹性分析的结果内力偏差,二阶弹塑性分析与一阶弹性分析的内力偏差普遍较大,同时其层间侧移的增大幅度明显大于内力的增加幅度,且偏于不安全。由此可见,铝合金框架结构设计只考虑二阶效应不能真实地反映铝合金框架结构的实际受力性能。
3)不论是6061-T6合金框架还是6061-T4合金框架,在达到名义屈服强度之前已有很明显的残余变形。二阶弹塑性分析与二阶弹性分析计算结果的内力偏差较大,且偏于不安全。可见,材料非线性引起的塑性效应影响显著,不能忽视。
4)当0.1 < ∑N·Δu/(∑H·h)≤ 0.25时,近似计算方法与二阶弹性分析的结果基本吻合。在此范围内,对于只考虑几何非线性的框架,现行规范的近似计算方法可代替二阶弹性分析。但从二阶弹性分析与二阶弹塑性分析的内力对比结果,可以发现不论是6061-T6合金框架还是6061-T4合金框架内力偏差都高达10%以上,由此可见,二阶弹性分析计算结果与实际受力情况偏差较大,现行规范的近似计算方法同样不能满足设计要求。
5)当∑N·Δu/(∑H·h) ≥ 0.25时,二阶弹性分析与二阶弹塑性分析的内力计算结果也偏于不安全较多,二阶弹性分析不能满足设计要求。
6)当∑N·Δu/(∑H·h) ≤ 0.1时,一阶弹性分析与二阶弹性分析的内力计算结果偏差普遍在5%以内,基本吻合。由此可见,在此范围内,对于只考虑几何非线性的框架,一阶弹性分析方法代替二阶弹性分析方法基本可行。但从一阶弹性分析与二阶弹塑性分析的内力对比结果,可以发现不论是6061-T6合金框架还是6061-T4合金框架内力偏差都高达10%以上,且偏于不安全,一阶弹性分析已不能满足设计要求。
综上,现行铝合金框架设计方法借鉴钢结构框架的设计方法,没有考虑材料非线性引起的塑性效应导致铝合金框架结构计算总体偏于不安全,且偏差很大。为了能反映铝合金框架结构的实际受力情况及精确地反映真实的塑性效应,无论铝合金框架结构的抗侧刚度如何,都应进行二阶弹塑性分析。
