基于特殊PID控制的多轴汽车转向性能仿真分析
2019-07-01
(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)
多轴汽车是指轴数大于等于3的车,如大吨位的长途运输车和特殊作业车。普通的多轴汽车转向时由于结构复杂、车体长等特点导致转向协调性差,转向过程容易发生失稳等危险工况[1]。目前多轴汽车的转向系统朝着多轴动态智能转向方向发展,希望所有车轮参与转向,实现不同转向模式的动态切换[2]。可根据不同的转向车速,调整多轴汽车的转向姿态,动态地控制汽车的操纵稳定性。
1 联合仿真模型
本文采用ADAMS与Simulink联合仿真的研究方法,首先建立ADAMS/View五轴汽车模型,其十个车轮均为转向轮而且能参与驱动。由ADAMS负责实现运动学仿真分析;MATLAB/Simulink完成控制系统以及轨迹跟踪;联合仿真实现软件间的互相通信。MATLAB/Simulink将控制系统的指令发送到ADAMS中,驱动五轴汽车模型,ADAMS再把反馈信息传到MATLAB/Simulink中的控制系统,由此形成反馈控制系统。图1为实现两者通信的adams_sub模块。

图1 联合仿真系统框图Fig.1 Block diagram of the co-simulation system
2 不完全微分PID控制策略
传统PID控制器是一种线性控制器,通过整定Kp、Ki、Kd的参数值实现对被控对象的控制,是经典控制理论中比较常用的一种方法。不完全微分PID控制是数字PID控制的一种,是在微分环节或者在整个PID控制器后边加低通滤波器,改善其高频干扰,图2为不完全微分算法的两种结构图,采用2(b)的结构形式。
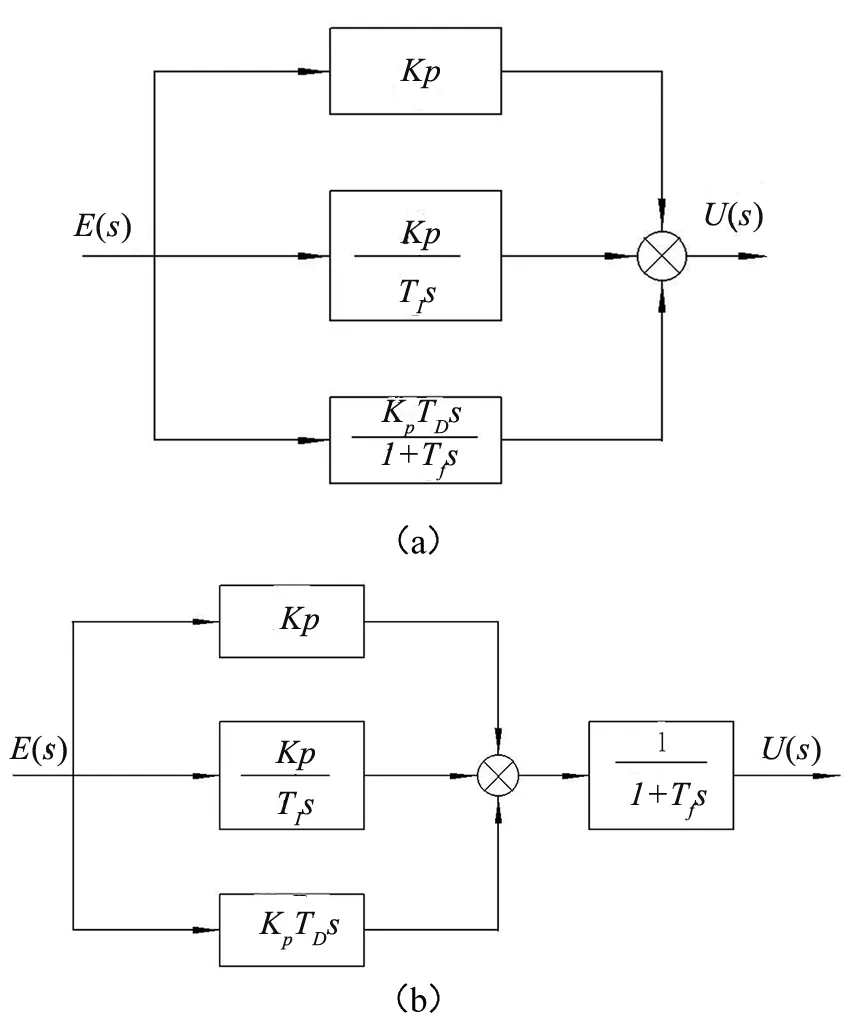
图2 不完全微分算法结构图Fig.2 Structure diagram of the incomplete differential algorithm
图2中,Kp为比例系数,TI和TD分别为积分时间常数和微分时间常数,Tf为滤波器系数,E(s)为系统的输入与输出之间的误差,U(s)为不完全微分PID控制器的输出。
采用不完全微分PID控制策略,控制目标为横摆角速度,实验输入不同的车速,实验车速为40、60、80、100 km/h,验证FD和CD两种状况在不同的车速下操纵稳定性参数的变化情况,以此分析FD和CD对整车角阶跃输入响应的影响,仿真时间为12 s。如图3所示为MATLAB/simulink中建立的控制系统仿真模型。
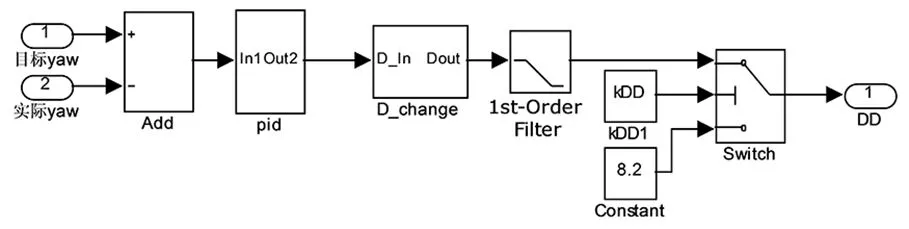
图3 控制系统仿真模型Fig.3 Simulation model of the control system

如图4(b)所示,PID控制的比例系数、积分系数和微分系数分别调为:Kp=200,Ki=12,Kd=10, 汽车采用滤波控制后曲线的局部振荡现象减缓,超调量减小,表明:不完全微分PID控制器控制的系统比常规的PID控制器更稳定。

图4 u = 60 km/h时D值的变化曲线Fig.4 Curve of D value when u = 60 km/h
不完全微分PID控制算法的其传递函数为:
uP(s)+uI(s)+uD(s)
(2)
将式(2)离散化为
u(k)=uP(k)+uI(k)+uD(k)
(3)
现推导uD(k)
(4)
写成微分方程为
(5)
取采样时间TS,将上式离散化为

(6)

uD(k)=KD(1-α)(error(k)-
error(k-1))+αuD(k-1)
(7)
由于不完全微分的uD(k)多了一项αuD(k-1),原微分系数由Kd降至Kd(1-α),加入一阶惯性环节能有效抑制高频干扰,改善系统性能。
由此得
error(k-1))+αuD(k-1)
(8)
3 五轴汽车全轮转向模型
为了方便研究五轴全轮转向汽车的转向性能,将多轴汽车模型转化为简单的二自由度模型分析,如图5所示,汽车质心为原点O,y轴平行于地面指向汽车前进方向,x轴指向驾驶员左边[3]。

图5 五轴汽车二自由度模型Fig.5 Two-degree-of-freedom model of the five-axle vehicle
由参考文献[5]可得多轴转向汽车的运动动力学方程
可将式(9)改写为

(10)

(11)
再由克莱姆法则计算得

(12)

(13)
多轴汽车的转弯半径为

(14)

由多轴转向车辆的阿克曼定理[7]得
(15)
式中,D为汽车转向中心与第1轴的距离;Lij为汽车第i轴与第j轴间的距离;B为轴距。
车轮在转向过程中应该满足纯滚动并且减少轮胎磨损,理想条件下各轮转角满足阿克曼定理。不同转向轴的同一侧车轮的转角关系应满足[8]
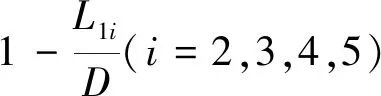
(16)
式中,Ki为各轴等效转角与前轴等效转角的比例系数。于是便有:δ2=K2δ1,…,δ5=K5δ1,代入式(4)和(5)。
(17)

(18)
于是有
(19)
由上式可知,多轴汽车操纵稳定性与质心位置、转向轮转角的比例关系、轴间距、各轴的侧偏刚度和车速等有关,而与各轴车轮偏转角大小无关,其中轴间距、各轴的侧偏刚度等车辆结构参数是固定不变的,无需调整,通过调整汽车转向中心与第1轴的距离D,即可调整转向轮转角的比例关系。基于此,多轴汽车在不同车速的路况条件下转向,多轴汽车转向系统通过对汽车转向中心与第1轴的距离D的控制,改善多轴汽车的操纵稳定性。
4 联合仿真与结果分析
采用ADAMS与Simulink对五轴汽车在不同车速下的转向性能进行联合仿真,如图6~图11所示。
4.1 CD控制策略的仿真分析
如图6所示,转向中心到第一轴的距离D的稳态值随着车速提高先提高后降低。

图6 不同车速下D的变化曲线Fig.6 Curve of D at different vehicle speeds
如图7所示,横摆角速度稳态值随着车速的提高而降低,说明汽车有较高的转向稳定性。

图7 不同车速下横摆角速度变化曲线Fig.7 Yaw angular velocity curve at different vehicle speeds
4.2 FD和CD控制策略的对比试验分析
如图8所示,选取固定的D值为8.2,7 s时转动多轴汽车方向盘,7.4 s时D值增加,D值变化率逐渐降低。

图8 u = 60 km/h时D值固定与D值变化的对比图Fig.8 Comparison of fixed D value and D value change when u=60km/h
如图9所示,速度提高质心的运动范围增加。在不同车速下,FD与CD的两种控制方式的质心运动轨迹基本重合,说明多轴汽车的轨迹跟踪性能较好。
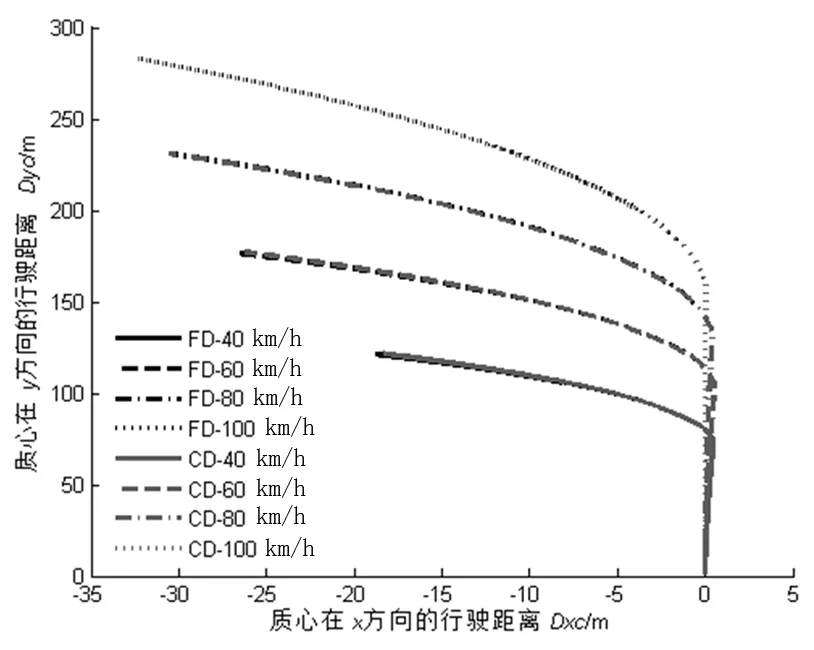
图9 质心运动轨迹曲线Fig.9 Trajectory curve of centroid motion
如图10所示,CD控制策略可以优化超调量和收敛时间,因此横摆角速度稳态值随着车速逐渐降低,CD控制方式的超调量低、收敛时间短,具有较好的控制性能。当车速为60 km/h时,FD控制策略的收敛时间为8.95 s,超调量为5×103rad/s; CD控制策略的收敛时间为8.2 s,超调量为1×103rad/s。由此可得,CD控制策略的横摆角速度的收敛时间可缩短8.38%,超调量可降低80%。

图10 不同车速下两种控制方式的横摆角速度对比曲线Fig.10 Comparison of yaw rate between two control modes at different speeds
如图11所示,侧偏角稳态值随着车速增加由负值变为正值。两种控制方式进行比较,车速增加,CD的侧偏角稳态值的绝对值更接近零(表1所示),因此CD控制方式更好。
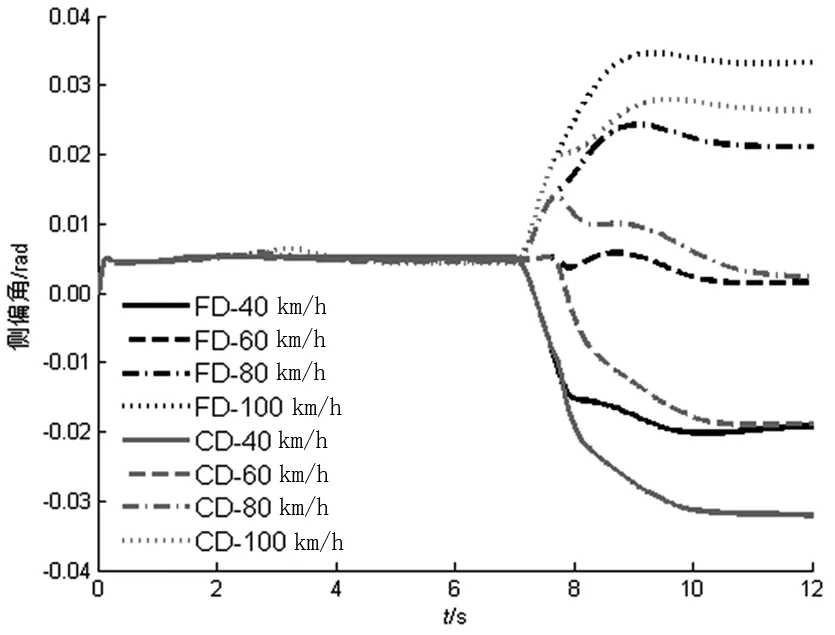
图11 不同车速下两种控制方式的侧偏角对比曲线Fig.11 Contrast curve of two control modes at different vehicle speeds

速度/(km·h-1)FD控制策略的绝对值/radCD控制策略的绝对值/rad400.0200.031600.0010.018800.0200.0021000.0330.025
5 结论
仿真结果表明,多轴汽车在转向的过程中动态地调整转向中心到第一轴的距离D能有效改善汽车的操纵稳定性。在高速时,FD和CD的横摆角速度稳态值基本相同,但系统的响应时间缩短,说明动态改变D的控制系统更灵敏,高速转向时更稳定。
