重载车辆在不平整路面的动荷载响应分析

孙吉书，李 猛，田红斌

(1. 河北工业大学 土木与交通工程学院，天津 300401； 2. 河北省土木工程技术研究中心，天津 300401)

0 引 言

车辆在路面上行驶时，因车辆自身振动与道路不平整共同产生动载作用，这一动载作用效果远大于道路规范设计当中静荷载对于路面动力影响效果，加快了路面平整度衰减速度，同时平整度衰减路面会增大车辆附加振动。故路面不平整度和车辆动荷载之间存在耦合关系，对重载车辆而言，其与路面不平整度之间耦合关系更甚，严重影响驾驶安全性和舒适性，同时也大大降低了道路使用寿命。

国内外学者针对车辆附加荷载基于路面结构动态响应过程已有较为深入研究。D.CEBON等[1]运用振动力学原理建立了路面激励下的车辆振动模型；I.V.SIDDHARTHAN等[2]运用有限元对支撑路面层状体系连续地基进行了研究分析，得出了路面动力响应，并基于轮胎和路面接触，应用傅里叶变换法实现了移动荷载对路面作用过程模拟；邓学均等[3]研究了因路面不平整度所引起车辆振动对路面的附加作用力；成祥生[4]利用变分法计算得出弹性地基支撑路面在边界条件、速度和振动影响下的动力响应；王直民等[5]应用疲劳损伤理论分析得出不平整路面上等效动荷载表达式；刘干斌等[6]将汽车荷载简化为矩形运动荷载，进行了路基路面结构动力响应研究。

现有研究虽针对路面不平整度基于车辆荷载影响进行了间接考虑，但并没有将车辆、路面结构看成一个系统进行建模，从而忽略了二者之间的耦合振动[7-9]。笔者在现有研究成果基础上，以四轴重载车辆组成特点和路面不平整度作为出发点，建立起车辆、路面耦合振动模型，进而推导计算车辆动荷载和动荷载系数得表达式，利用MATLAB软件得到车辆最大动荷载随着行车速度变化规律；及最大动荷载随波长、振幅和载重变化规律。

1 四轴重载车辆振动模型

车辆作为一个复杂的多自由度振动系统，为确保建立的车载振动模型与车辆实际运行情况相适应，并能简化研究过程，笔者作出如下假设：

1)将车身视为刚体，与垂直面对称；

2)车辆只做竖向振动和俯仰振动，亦即路面垂直方向上的激励作用；

3)位移一次函数为弹性单元刚度，位移二次函数为阻尼；

4)建立四轴车辆的1/2模型，且车轮横向两侧受到不平整激励相同；

5)车辆前后轮具有重合行驶轨迹，位移车身同一侧前后轴车轮平整度激励受到前后轴距单一因素影响。

1.1 车辆振动模型

车辆振动模型如图1。图1中：m1、m2分别为拖车簧下质量；m3、m4分别为挂车簧下质量；m5为拖车簧上质量；m6为挂车簧上质量；k1、k2、k3、k4分别为轮胎刚度；k5、k6、k7分别为悬架弹性元件刚度；c1、c2、c3、c4分别为轮胎阻尼；c5、c6、c7分别为悬架阻尼器阻尼；J1、J2、J3分别为拖车、挂车、平衡悬架的转动惯量；a1、a2、a3分别为拖车前轴、铰接点、拖车后轴到拖车质心距离；b1、b2分别为铰接点、挂车平衡悬架中心到挂车质心距离；d为平衡悬架长度。

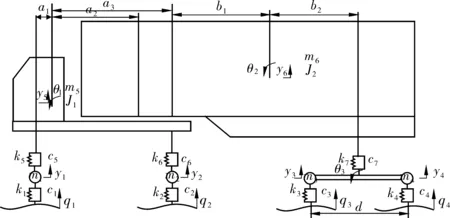
图1 四轴车载振动模型Fig. 1 Four-axle vehicle vibration model

求解上述7自由度四轴重载车辆平面模型[10]的振动方程为一组相互耦合的二阶常微分方程组。其中微分方程数量较多，且各微分方程之间存在坐标耦合，求解过程较为困难，为简化计算，可将该模型分解为两个双自由度和一个三自由度简化车载振动模型[11]，如图2。

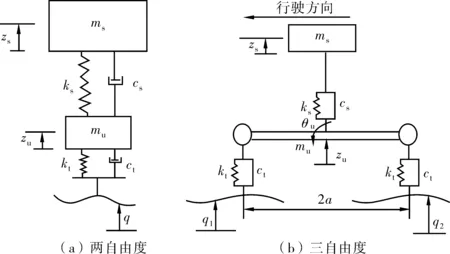
图2 车载振动模型Fig. 2 Vehicle vibration model

图2中：ms为簧下质量；mu为簧上质量；kt为轮胎刚度；ks为悬架弹性元件刚度；ct为轮胎阻尼；cs为悬架阻尼器阻尼；Iu为颠簸惯量；a为1/2双轴间距；q、q1、q2分别为路面不平整度；zs为悬挂系统垂直位移；zu为非悬挂系统垂直位移；θu为双轴转动角。

1.2 车辆振动运动方程

上述两种振动模型的力学微分方程如式(1)：

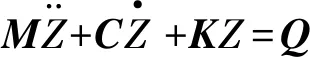
(1)

矩阵形式的双自由度车载振动模型如式(2)：

(2)

矩阵形式的三自由度车载振动模型如式(3)：

(3)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Y为位移矩阵；Q为激励矩阵。

现阶段对路面平整度表达一般采用MW.Sayers正弦波表达法[12]，因此路面振动激励函数如式(4)、(5)：

两自由度：q1=Asin[ωt]

(4)

三自由度：q1=Asin[ωt+α]

q2=Asin[ωt-α]

(5)

式中：A为路表振幅；ω为角频率，ω=2π/λ；λ为波长；α为初始相位角，α=2πa/λ；t为路面水平方向位移量。

1.3 车辆振动运动方程求解

1.3.1 双自由度车辆振动运动方程求解

式(2)可整理如式(6)：

(6)

令y1=zu-z0，y2=zs-zu，f1=ct/mu，f2=cs/ms，μ=ms/mu，g1=ms/mu，g2=ks/ms，带入式(6)得到式(7)：

(7)

利用待定系数法，可设：

(8)

将式(8)带入式(7)，可得到式(9)：

(9)

借助MATLAB编写程序，对式(9)求解，可求得R1～R4表达式，之后带入车辆振动荷载表达式(10)中：

(10)

可得车辆最大振动荷载，如式(11)：

Pdm=(ms+mu)g+

(11)

1.3.2 三自由度车辆振动运动方程求解

对三自由度车辆振动运动方程求解，可利用待定系数法，如式(12)：

(12)

将式(12)带入式(3)中，整理可得式(13)：

(13)

借助MATLAB，对式(13)求解，可求得R1～R6表达式，之后带入到车辆振动荷载式(14)～(17)当中：

sin(ωt+γ1)

(14)

sin(ωt+γ2)

(15)

当sin(ωt+γ1)=sin(ωt+γ2)=1时，可得到车辆最大振动荷载：

(16)

2 车载振动模型计算与分析

2.1 车载振动模型参数

以四轴重载车辆作为分析对象，建立起了重载车辆振动模型，将该模型简化分解为两个双自由度和一个三自由度的简化车载振动模型。由四轴重载车辆的振动参数可推导出双自由度和三自由度简化车载振动模型参数，如表1。

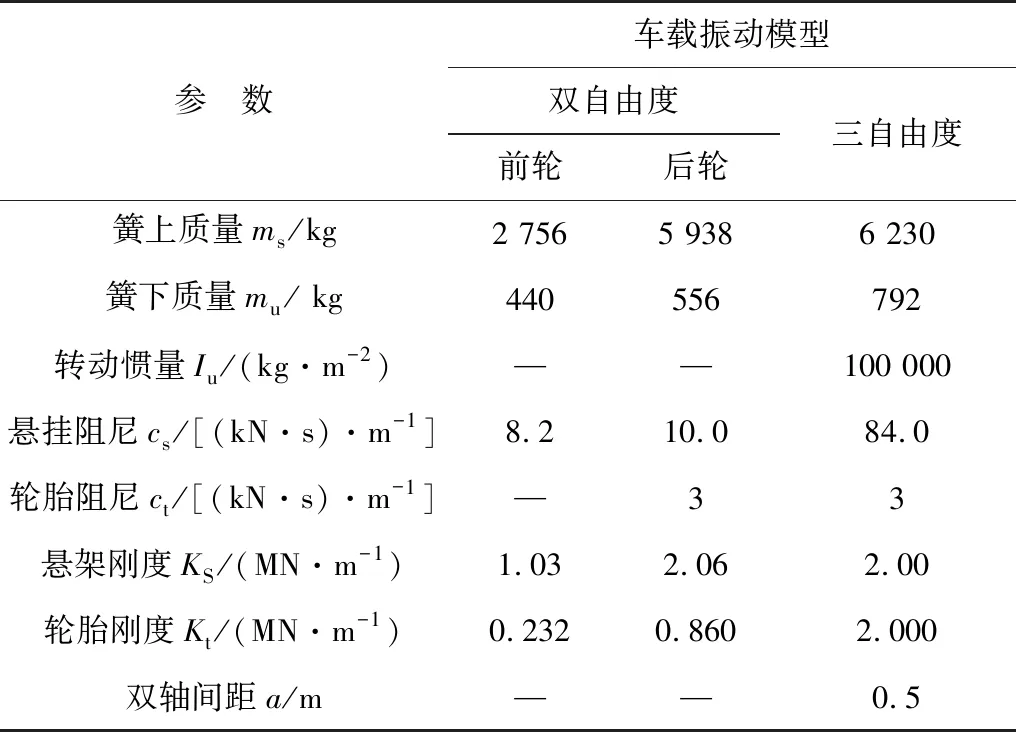
表1 车载振动模型参数Table 1 Vehicle vibration model parameters

2.2 车辆竖向附加振动荷载

为更加准确研究重载车辆在不平整路面上振动响应情况，笔者应用最大动荷载概念，对车辆因振动对路面造成的动荷载进行描述。

通过MATLAB对四轴重载车辆两个双自由拖车前轮、拖车后轮和一个三自由度挂车前轮、挂车后轮车载系统的最大动荷载随车速变化规律进行分析，并找出产生最大动荷载的车轮；并分析该车轮最大动荷载随波长、振幅和载重变化的规律。

2.2.1 车载系统最大动荷载随车速变化规律(图3)

由图3可看出：车辆在行驶过程中，动荷载随车辆速度保持动态变化；4个车轮动荷载随车辆速度增加，都先后经历下降—升高—下降的过程，其中拖车前轮与后轮变化趋势较为明显，挂车前轮与后轮的变化趋势较为平缓。

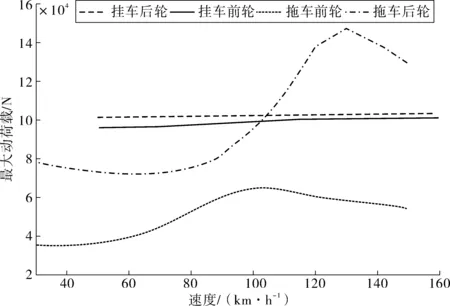
图3 最大动荷载随车速的变化规律Fig. 3 Variation rule of maximum dynamic load changing withvehicle speed

通过曲线对比可看出：在车速为100 km/h时，挂车前后轮与拖车后轮这3者最大动荷载相差不大。在实际车辆行驶过程当中，车辆速度往往会超过规定的最大速度，当超过规定最大速度时，拖车后轮最大动荷载急剧上升，且迅速超过挂车前后轮；故拖车后轮对不平整路面产生的动态影响最大，所以通过研究拖车后轮所产生动荷载与路面波长、幅值和载重关系能更直观的了解重载车辆在不平整路面的动荷载响应。

2.2.2 路面波长与拖车后轮动荷载关系(图4)

车辆振动系统随路面不平整度波长不同而变化。国际道路协会常设委员会(PLARC)规定，路面不平整度波长一般为0.5～50 m，图5描绘了相应波长范围的最大动荷载变化曲线。由图5可知：随着波长增加，最大动荷载出现两个峰值，第一个峰值出现在波长为0～5 m范围内，第二个峰值出现在8～25 m范围内；且第二个峰值明显高于第一个峰值；随着速度增加，两个峰值出现所需波长更长，且不同峰值在速度不同时基本对应相等；当路面不平整度波长增加到一定程度时，最大动荷载趋近车辆振动系统自重，此时可认为路面趋于平整。

图4 最大动荷载随波长的变化规律Fig. 4 Variation rule of maximum dynamic load changing withwavelengths

2.2.3 路面振幅与拖车后轮动荷载关系(图5)

由图5可看出：不同速度下，最大动荷载与路面振幅成正比，且在相同振幅之下，速度越大，最大动荷载则越大。路面振幅一般代表路面颠簸程度，路面越颠簸所产生的动荷载越大，这与实际经验情况相符合，故控制路面不平整度，减小路面振幅，是减小振动荷载、增加行车舒适性的重要途径。速度越大，最大动荷载增长速率越大，这是由于路面不平整度和车辆动荷载之间存在耦合关系，故随着车辆速度增加，会加剧车辆振动，进而增加最大动荷载变化速度。

图5 最大动荷载随幅值的变化规律Fig. 5 Variation rule of maximum dynamic load changing withamplitude

2.2.4 载重与拖车后轮动荷载关系(图6)

由图6可看出：当车辆满载之后，最大动荷载随着满载倍数增加而增大，且呈现出线性增加趋势；在相同满载倍数情况下，车辆速度越快，产生的最大动荷载越大，但不同速度下的最大动荷载增长速率相等，故超载问题是影响道路使用寿命的主要“杀手”；超载车辆较满载车辆相比，产生最大动荷载更大，因此对路面造成的损害更为严重。为保障道路给行车过程带来更高水平舒适性，应当严格控制车辆的载重和超速。

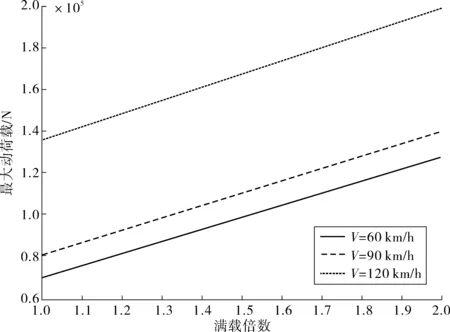
图6 最大动荷载随载重的变化规律Fig. 6 Variation rule of maximum dynamic load changing with load

3 结 论

1)由于路面不平整度和车辆动荷载之间存在耦合关系，故路面不平整度会使车辆在行驶过程产生动荷载，这种动荷载在重载交通车辆上表现得更为明显。笔者根据沥青路面特性，以正弦波形路面作为激励，建立四轴重载车辆的7自由度(1+1+5)车辆振动模型，为简化计算，将该模型分解为两个双自由度和一个三自由度车载振动模型。

2)借助MATLAB程序实现车辆动荷载计算，并分析了四轴重载车辆最大动荷载随速度变化规律，找出产生最大动荷载车轮为拖车后轮。

3)研究了拖车后轮最大动荷载随波长的变化规律，随着不平整度波长的增加，最大动荷载出现两个峰值，不同的峰值在速度不同时基本对应相等，第二个峰值明显高于第一个峰值，当路面不平整度波长增加到一定程度时，最大动荷载趋近车辆振动系统自重，此时可认为路面趋于平整。

4)路面振幅对动荷载影响较大，这也验证了路面不平整度是动荷载产生的主要原因。故对平整度较差的路面，驾驶人应适当降低初速，有关部门应及时对道路进行维护，避免路面进一步损坏。

5)超载问题是影响高速公路使用寿命的主要“杀手”。超载车辆与满载车辆相比，产生的最大动荷载更大，对路面造成的损害也更严重。为避免道路进一步损坏，增长其使用寿命，有关部门应严格控制车辆超载现象。