基于二阶快速终端滑模的感应电机速度控制*

杨晓辉，付珍峰，周斯易

(1.南昌大学 信息工程学院，南昌 330031；2.国网江西省电力有限公司湖口县供电分公司，江西 九江 332500)

0 引言

感应电机是一个多变量、强耦合的非线性系统，当调速系统发生参数变化、负载扰动等不确定因素的影响时，传统的PI控制器难以满足实际的控制需求[1]。近年来，随着现代控制技术的发展，一些先进的控制策略逐步被应用到感应电机调速系统，提升了系统的鲁棒性和动态性能[2-6]。

其中，滑模变结构控制因其对模型精度要求低、计算量少、对系统参数和外部扰动具有强鲁棒性等优点成为国内外学者研究的热点。在滑模控制中，滑模面的选取至关重要，目前滑模控制采用的滑模面主要有：线性滑模、积分滑模、分数阶滑模、终端滑模(termina sliding mode，TSM)、非奇异终端滑模(nonsingular terminal sliding mode，NTSM)等[7-11]。其中Zak提出的终端滑模控制在滑模超平面的设计中引入非线性函数，使得在滑模面上跟踪误差能够在有限时间内收敛到零，突破了普通滑模控制在系统到达滑动模态后只能渐进收敛的问题,具有动态响应快、稳态精度高等优点[12]。但是普通终端滑模控制的收敛速度却并不是最优的。为了进一步提高感应电机调速系统的控制性能本文从提高收敛速度和抑制抖振两个方面综合考虑，设计了一种二阶快速终端滑模控制器(FTSM)。仿真结果通过和PI控制器和普通TSM控制器的对比，证明了该速度控制器的有效性和优越性。

1 感应电机数学模型

假设感应电机三相定、转子绕组分布均匀对称，忽略磁路不饱和、铁芯损耗以及温度和频率对转子电阻产生的影响。在按转子磁链定向的同步旋转坐标系(m-t坐标系)中，以ω-is-φr为状态变量的状态方程可表示为：

(1)

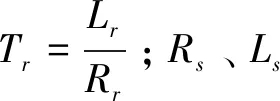
2 二阶快速终端滑模控制器设计

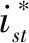
e=ω*-ω

(2)

2.1 快速终端滑模面

(1)传统终端滑模面

传统的终端滑模可由如下一阶动态方程描述：

(3)

其中,x∈R为状态变量，λ>0，α，β(β>α)为正奇数。方程(2)在平衡点x=0附近的Jacobian行列式为：

(4)

把J看做一阶近似矩阵的特征值，则有：x→0+，J→-∞。即在平衡点附近系统轨迹的收敛速度为无穷大，从而导致系统状态可以在有限时间内到达平衡点。

设系统状态从任意初始状态x(0)≠0到达平衡点x=0的时间为tr，则由方程(3)可以求得：

(5)

(2)快速终端滑模面

终端滑模控制可使系统跟踪误差在有限时间收敛到零，系统动态性能优于普通的滑模控制，但是普通终端滑模控制的收敛速度却并不是最优的。由式(4)可知，当状态远离平衡点时行列式的的绝对值很小，也就是说系统状态离平衡点越远，其收敛速度越慢。文献[13]在终端滑模的基础上提出了一种新的快速终端滑模控制，其滑模面可由如下方程来描述：

(6)

其中,x∈R为状态变量，λ1>0，λ2>0，α，β(β>α)为正奇数。方程在平衡点x=0附近的Jacobian行列式为：

(7)

同样，有x→0+，J→-∞，系统可以在有限时间tf内到达平衡状态。可解得从任意初始状态x(0)≠0到达平衡状态x=0的时间可以表达为：

(8)

由式(7)可知当状态x远离平衡点时行列式J的绝对值将恒大于λ1，因此线性滑模控制的引入在保留了终端滑模有限时间收敛的特性的同时，又增加了线性滑模控制在远离平衡点时的快速性，使得系统快速、精确地收敛到平衡点。

2.2 二阶快速终端滑模速度控制

将式(2)带入式(1)可得转速误差系统：

(9)

设计快速终端滑模面为：

(10)

其中,a1>0，a2>0，α，β(β>α)为正奇数。

根据函数切换控制法可设计快速终端滑模控制器为如下形式：

(11)

其中,ieq为等效控制量，in为切换控制量。等效控制量是控制系统在切换平面做滑动模态运动时的控制量，切换控制量是为了确保系统在遇到干扰的情况下，仍然能趋近于滑模面且沿着滑模面运动，由式(9)和式(10)得：

(12)

切换控制项通常设计为：in=η0sgn(s)的形式，为保证系统鲁棒收敛需要选择大的非线性增益η0，但这会造成较大的抖振，甚至激发未建模动态，使系统不稳定。为了解决这个问题，本文对切换项采用二阶滑模控制，控制律设计如下：

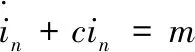
(13)

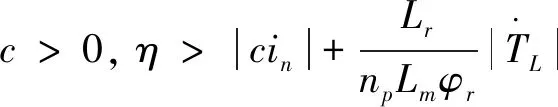
2.3 稳定性分析

为证明系统式(10)在控制器式(12)、式(13)作用下的稳定性，定义李雅普诺夫函数：

(14)

对上式求导可得：

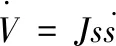
3 仿真及结果分析

为验证所设计二阶快速终端滑模速度控制器的有效性，使用MATLAB/Simulink搭建如图1所示的按转子磁链定向的感应电机矢量控制系统进行仿真验证。仿真实验中感应电机参数如下：

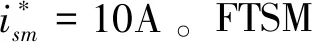
a1=40，a2=50，c=10，η=5000。

电机空载启动，初始给定转速为500r/min,0.5s时给定转速增加到1000r/min，1s时突加10N·m的负载，仿真时间为1.5s。图2分别为PI、TSM、FTSM控制的转速响应图。

对转速响应图进行局部放大可知电机转速从0r/min调节到500r/min，PI、TSM、FTSM的时间分别为0.14s、0.08s、0.08s；从500r/min调整到1000r/min的时间分别为0.61s、0.58s、0.57s。可见，FTSM控制的性能明显优于PI和TSM控制。

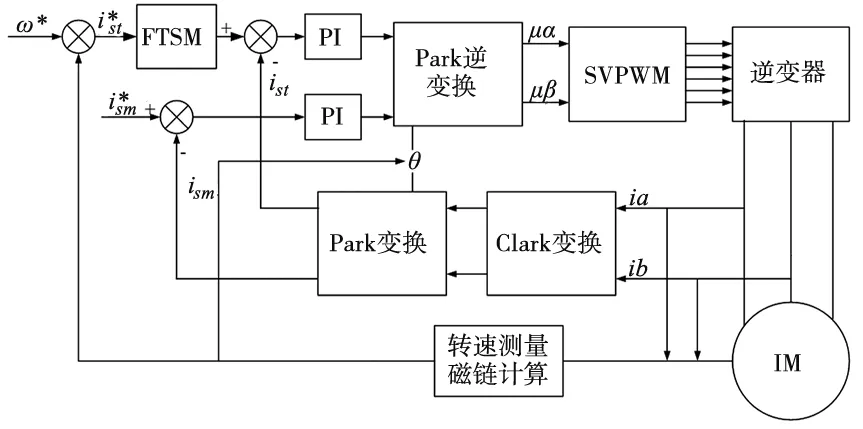
图1 感应电机调速系统框图

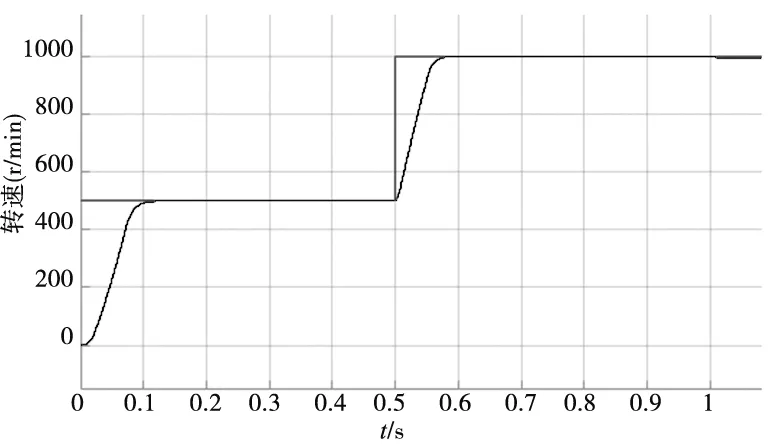
(a) PI

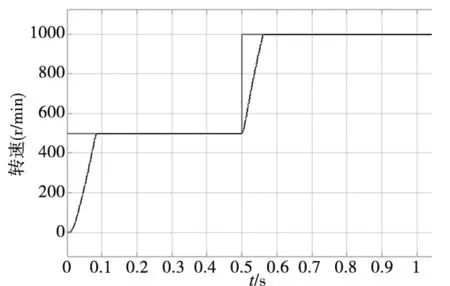
(b) TSM

(c) FTSM 图2 转速响应图

1S突加负载后感应电机转速响应如图3所示。

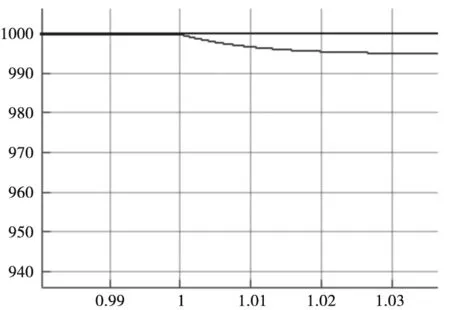
(a) PI

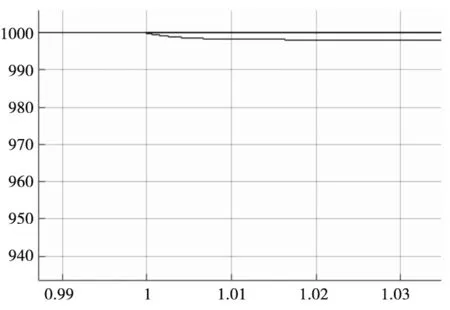
(b) TSM

(c) FTSM 图3 突加负载转速响应图

可以看出PI控制下调速系统有明显的转速降落，TSM控制转速降落较小，而FTSM控制依然基本无误差，可见FTSM在电机突加负载时具有明显的优越性。

为验证所设计二阶控制对抖振的抑制作用，分别在有二阶控制和无二阶控制下进行仿真实验，仿真结果如图4所示。

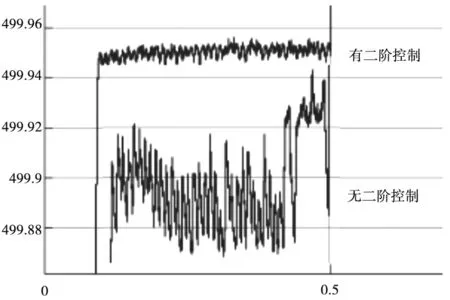
图4 有二阶控制和无二阶控制下的转速响应图

由式(13)可知，本文对切换控制项设计的二阶控制律等效于将切换控制量通过一个低通滤波器，由图4可以看出在经过低通滤波器之后稳态转速的波动幅度从0.1r/min降低到了不足0.02r/min，可见二阶控制的有效性。

4 结论

为了提高感应电机调速系转速调节性能，本文提出了一种二阶快速终端滑模转速控制算法。建立了感应电机在两相同步旋转坐标系下的数学模型，分析并设计了快速终端滑模控制律。同时，为了削弱抖振，设计了作用于切换函数导数上的二阶控制律。通过与传统PI控制和普通TSM控制相比较，验证了控制算法的优越性。通过与无二阶控制的快速终端滑模控制相比较，验证了二阶控制削弱抖振的有效性。