基于改进的FCM聚类算法对温度测点的优化和建模*

赵家黎，吴丽媛，黄利康，胡赤兵

(兰州理工大学 机电工程学院，兰州 730050)

0 引言

在机床工作状态下，机床的各零部件产生的摩擦热、切削热以及外部热源引起的热变形，从而降低了机床的加工精度[1]。大量的研究表明，在机床加工过程中，机床热误差影响非常严重，60%～70%的机床误差是由热误差造成的，因此解决热误差是当务之急[2]。而主轴是机床的核心部件，在机床加工零件时，热误差主要来源于电机及主轴前、后轴承等部位发热，从而使主轴在X、Y、Z方向发生了热变形或实际零件加工点的偏移。因此，控制并减少机床各部件的热误差是机床加工精度提高的必要前提。针对主轴热误差问题，国内外学者从以下三方面进行展开研究：①对主轴箱内部机械结构和传动结构进行简化或取消，从而减少 各零部件之间产生的热源，提高了机床的加工精度[3-4]; ②在实际加工测量中，将主轴测量的变形量反馈给控制系统，从而实现在线修正误差[5]; ③通过对主轴各方向产生的热变形机理分析的基础上，建立温度与热变形量关系模型，从而对加工误差实施静态或动态补偿[6]。综上，可以通过控制温度的方法实现误差的控制，具有一定的局限性。因此，运用第三种建模方法实现误差补偿是目前广泛使用的。

许多学者对主轴热误差进行了大量的研究，也提出了很多值得探讨的方面。随着机床外部温度、机床的主轴转速、各进给轴进给转速以及机床的负载变化使得预测模型补偿精度不能得到很好的体现。而且在机床切削过程中，更能接近机床运行的真实状态，对温度传感器位置的布置和对测得温度数据的优选方面，值得进一步探究，找出机床主轴引起热误差主要原因，对所测得数据进行筛选使其更好表达机床的真实温度变化并且准确的预测机床热误差模型。基于以上问题，该论文以教学型复合机床主轴主题，提出基于改进模糊C均值聚类(Improved Fuzzy C-means, IFCM)算法，对机床测量的温度值进行分组和筛选，选出每组最优的温度值进行迭代，采用多元线性回归理论建立机床主轴热误差预测模型，使用机床主轴热误差实验测量数据对多元线性回归热误差模型进行验证。

1 热误差温度测点优化

针对温度传感器的布置和测量的温度数据的提取这一问题，提出了改进模糊C均值聚类算法的研究，分析温度点的变化与热误差之间的关系。

1.1 传统的FCM聚类算法

FCM算法是用隶属度确定每个数据点属于某个聚类程度的聚类算法[7]。

y={y1，y2，…,yn}为温度点的集合，n为测量温度的温度传感器个数。将样本y划分为c类温度小组，计算每组的温度聚类中心ci，FCM目标函数[8]定义为：

(1)

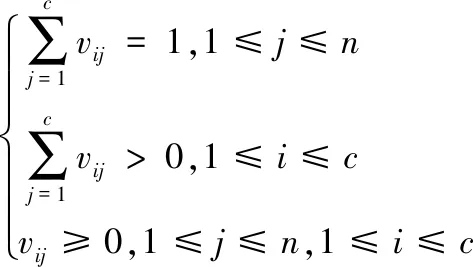
(2)

式中，vij是i×j的模糊划分矩阵，且表示第j个温度点样本yj属于第i类温度隶属值；eij=ci-dj表示ci温度点到dj温度点的欧氏距离；m>1表示加权指数。

对公式(1)进行最小二乘法得到的表达式为：

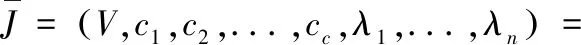
(3)

式中，λj表示拉格朗日乘子，对输入参数进行求导，则公式(1)取得最小值的条件如下所示：

(4)

(5)

对公式(4)和公式(5)不断进行迭代，直到满足：

(6)

其中，ε表示收敛精度，h表示迭代次数。FCM算法的步骤：

①隶属矩阵V满足公式(2)的条件。

②利用公式(4)计算c个聚类中心ci。

③利用公式(1)求解目标函数，如果所得值差于上次目标函数值，则聚类算法停止。

④利用公式(5)求解新的矩阵V。

1.2 改进的FCM聚类算法

由于FCM聚类算法对初始聚类中心比较敏感，所以容易得出局部最优解[9]。FCM聚类算法采用经验划分的方法，所以划分方法本身就存在缺陷，对测量的温度点的实际分布情况不能正确的划分，得到的初始聚类中心也是有一定的差距，针对欧式距离的缺点进一步改进，然后采用一种度量因子的方法选取初始聚类中心，改进了传统的FCM聚类算法中的初始聚类中心的缺陷。

1.2.1 对欧氏距离的改进

由于欧式距离没有考虑到两个温度点在各分量的分布，所以采用标准化欧氏距离对欧氏距离改进，其思路是在整个温度数据中，各数据各维分量的分布不一样，先对各个分量都标准化到均值、方差等，从而得到均值分布或方差分布。假设样本集y的均值为m，标准差为s，y的标准化标量表示为：

(7)

则标准化欧氏距离公式为：

(8)

将式(8)代入式(1)进行迭代，再根据FCM聚类算法步骤进行迭代得出隶属度矩阵。但欧氏距离改进不能使初始聚类中心正确选择。下面使用度量因子的方法对初始聚类中心进行确定。

1.2.2 度量因子的确定

对传统的FCM聚类算法随机选取初始聚类中心的方法，提出了使用度量因子选取聚类中心。定义一个聚类中心近似度量为Q，表示第i个温度点yi到任意温度点的距离，表示为：

(9)

其中，φ为一个常数。

改进FCM聚类算法的步骤为：

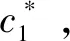
(2)计算每个温度点与该点聚类中心的隶属度值，根据隶属度值，将点C1*和与C1*具有很高隶属度值的样本从下一次迭代中移除，防止产生伪聚类中心；

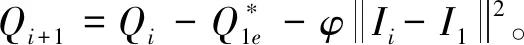
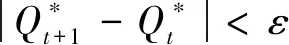
2 多元线性回归模型

2.1 理论建模方法

利用多元线性回归理论建模，是运用统计方法建立多个输入、单个输出的关系模型[11]，该理论针对加工机床热变形的具体情况，通过实验、计算得到一组表达多个测量点温升输入、单个方向上位移变化输出的线性关系。由于教学型复合机床的主轴热变形在X、Y、Z三个方向上，因此在三个方向上分别独立的求出一组关系式，且满足线性关系。

假设模型中随机变量y与n个自变量x1,x2,…,xn之间存在某种内在联系。随机变量y与相关的自变量x1,x2,…,xn之间存在某种线性模型，其表达式[12]如下所示:

y=f(x1,x2,...,xn)+ε

(10)

式中，f表示约束函数，ε表示随机误差。

若公式(10)中回归函数是线性关系时，并且(yt;xt1xt2,…,xtn),t=1,2,…,n是因变量和自变量m组样本观测数据，则有如下所示：

(11)

由公式(10)转换为多元线性回归的数学模型：

Y=AX+ε

(12)

其矩阵形式为：

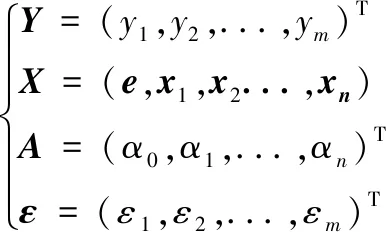
(13)

其中，Y为因变量向量，X为自变量向量，A为系数矩阵，ε为随机向量。从正态分布的定义可知，ε1,ε2,...εn是相互独立且服从同一正态分布N=(0,σ2)。

设α0,α1...αn的最小二乘估计值分别是μ0,μ1,...,μn，则多元线性回归方程表示为：

y=μ0+μ1x1+...+μnxn

(14)

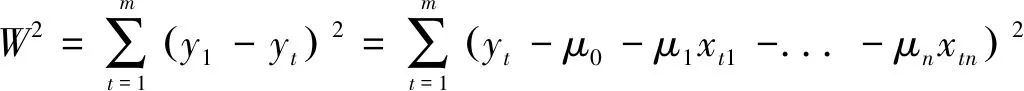
由数学分析中的极小值原理得到：

(15)

将因变量y和自变量x的m组样本值代入式(15)，即可求得回归参数μ0,μ1,...,μn代入式(11)，便可得到因变量与自变量之间的多元线性回归方程。

2.2 热误差模型的建立

由于教学型复合机床在运行时它的温度场是随着时间的变化而连续变化的。为了测量机床主轴X、Y、Z方向的热误差，必须通过温度传感器测量机床主轴各个部位得到相对应的温度值T1,T2,…,Tn。利用改进的FCM聚类算法筛选出最优的温度点进行建模。对筛选出的关键温度点进行多元线性拟合，从而得出热变形和温度的关系表达式[13]如下所示:

(16)

其中，α0i,αij分别表示各个测量温度点误差相关系数，i=1,2,…,n表示测量的温度点数量，j=1,2,…,k表示测量温度的次数。

3 实验验证与分析

本文是以多元线性回归理论预测模型应用于教学型复合加工机床主轴热误差进行测量试验，采用改进的模糊C均值聚类方法，通过温度传感器的测量，选择温度敏感点，从机床上布置的 15 个温度传感器中，具体测点分布为：主轴电机支架(1)，主轴前端(2，7)，主轴后端(3，8)，主轴箱(4，9，10，11)，立柱(5，12，13，14)，机床床身(6，15)。经过筛选后确定了4、7、8、5号共4个测点，用这4个测点的所得到的温度值作为建模的输入参数，进行多元线性拟合，得到的误差预测曲线与实验的测量值进行对比。见图1、表1及图2所示。

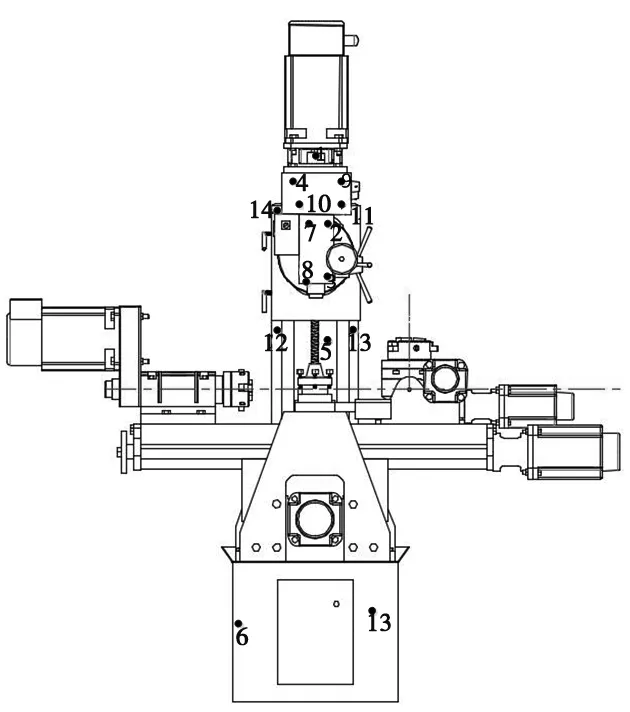
图1 机床温度传感器整体分布图

传感器编号传感器位置作用 4主轴箱测量主轴箱热变形7主轴前端测量主轴温度8主轴后端测量主轴温度5主轴电机测量电机发热

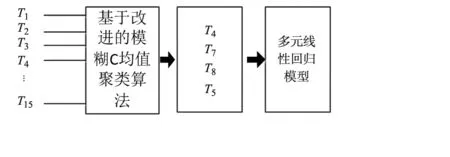
图2 复合机床热误差建模流程

在温度测量实验中，为了分辨机床主轴的热特性，使机床主轴的转动更能体现出机床实际加工工件的状态，从而测量出主轴温度变化规律。因此，选择不同的主轴转速测量温度的变化，得出接近真实的温度数据，为后续的补偿提供有效的数据。实验方案：机床主轴转速在600r/min,运转时间为60min，然后选择主轴转速为1200r/min，运转时间为60min，每隔10min测量一次温度值。对机床主轴的X、Y、Z方向各测量2h，所得到的温度数据可以看出，机床主轴X方向的热变形量符合使用要求的范围且在±0.015mm以内，因此无须进一步分析。本文只对主轴Y方向和Z方向受温度影响进行分析，运用多元线性回归模型进行线性拟合。主轴Y方向和Z方向热误差如图3及图4所示。

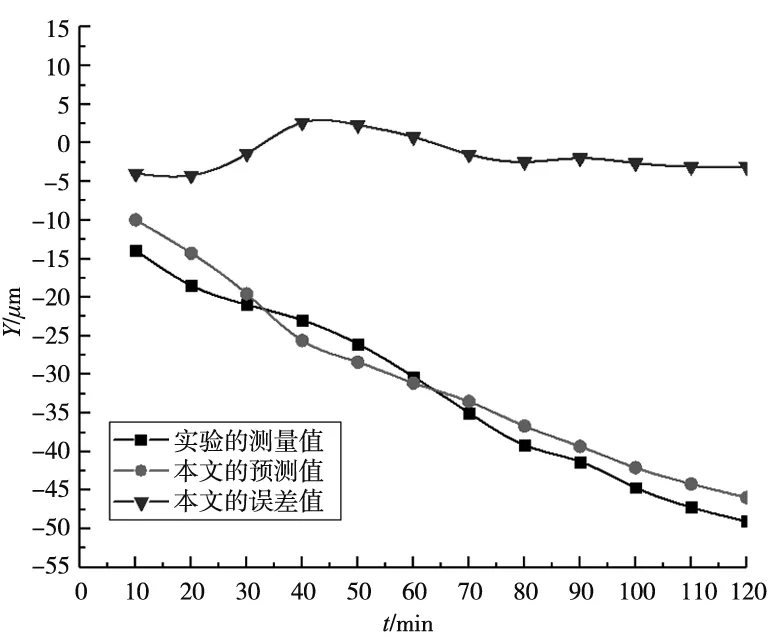
图3 主轴Y方向热误差

图4 主轴Z方向热误差

根据图3、图4分析可知：对复合机床主轴热误差补偿前，主轴Y方向受温度影响产生的最大误差为49.0134μm，主轴Z方向受温度影响产生的最大误差为35.96328μm；对复合机床主轴热误差进行补偿后，主轴Y方向受温度影响产生的最大误差为4.18778μm，主轴Z方向受温度影响产生的最大误差为5.31307μm，误差在5.4μm以内。因此，运用多元线性回归预测模型对主轴的预测值和实际值进行对比分析，可得到较小误差，使得复合机床主轴运行时产生的误差通过补偿后得到了明显的提高，从而提高机床精度。

4 结束语

在测量机床热误差的实验过程中，得到的温度数据通过使用改进的模糊 C 均值聚类法对采集到的数据进行筛选，选择出每组最优温度测量数据，使温度测量数据大幅度减少，从而降低了建模的运算量。采用多元线性回归理论，有利于提高温度传感器布置的鲁棒性。依据实验数据分析可知，主轴以不同转速转动时，得到的多元线性回归模型有效的验证了预测的可行性，从而提高热误差的预测精度，可作为数控机床热特性的评估参照。